含氮污染物耦合算法联合优化研究
肖 飞,董文明,王维红
(新疆农业大学 水利与土木工程学院,乌鲁木齐 830052)
鉴于污水深度处理[1-2]工艺化学试剂用量大、运营投资成本超标,同时污泥产率增加引起微生物分泌物增多[3-4],使部分工艺无法稳定运行[5-6],从而导致二次污染和含氮化合物排放超标等问题。为使城市污水处理厂出水氨氮及总氮实现稳定的达标排放,国内外学者提出了基于数学模型优化控制衍生出的多目标优化方法的研究[7]。赵小强等[8]采用改进多目标布谷鸟算法,实现废水处理过程的多目标最优控制,结果表明:在出水水质参数达标的前提下,能有效地降低模型耦合过程废水处理的能耗。Vega等[9]将基于二次序列分层优化算法与非线性模型预测控制理论(RO-NMPC)相结合,结果表明该模型可确保出水水质达标的基础上减少能耗,与赵小强等[8]的研究结果相似。韩红桂等[10]建立自适应核函数的动态性能指标模型,实现了溶解氧和硝态氮的动态控制。另外,李霏等[11]针对污水处理过程出水水质严重超标等问题,提出了一种基于均匀分布的NSGAⅡ多目标优化智能控制系统。通过对优化设定值进行底层跟踪控制,证实所提出的UDNSGAⅡ多目标优化控制方法的有效性。其次,Syafiie等[12]基于强化学习算法的优化策略,提出在保证污染物排放达标的同时,可优化废水处理运行能耗。
然而,基于多目标权重系数法的实际优化效果并不理想。针对上述问题,以新疆某Ⅱ期运营污水厂为研究对象,提出了一种基于耦合灰度-多目标约束粒子群(GM-MOPSO)的最优化算法。与此同时,权衡污染源和出水水质间的关系,进行多目标约束优化条件,从而建立废水处理自适应回归核函数的水质参数模型,旨在利用多目标粒子群算法对废水处理出水水质模型进行优化,以此降低出水总氮含量,确保出水达标排放。
1 污水处理过程分析
1.1 灰色理论
1.1.1 GM模型
灰色理论诞生于1982年,由邓聚龙首次提出[13],它是一种研究少数据、贫信息、转换序列不确定性问题的新方法。同时,以灰色系统建立的模糊预测模型称为灰色模型(GM),它是基于原始数据序列的微分方程,并以时间序列GM(i,N)为主的灰度预测。
1.1.2 灰色预测
本文采用灰色模型[14]GM(1,5)估测总氮(TN)的去除率,此模型主要基于历史记录信息建立累积生成序列,通过生成序列数据矩阵和矢量微分来建立带有系数的方程,将生成的系数转化为微分方程的通用公式,然后再产生序列估计误差。具体计算过程如下:
1)以原始数据序列作一次累加生成(AGO),使生成序列呈增长规律。
3)对x(0)i进行一阶累加生成,即得模糊模型1-AGO。
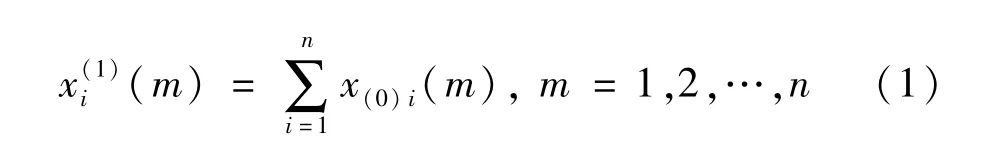

其中m取值范围为[2,n]。

则GM(1,5)的灰微分方程模型为
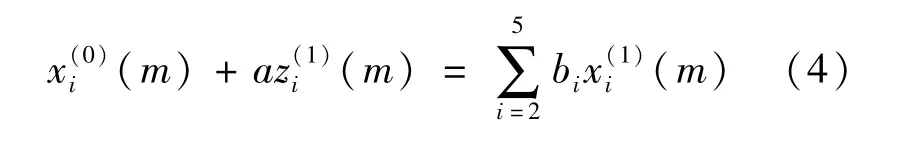
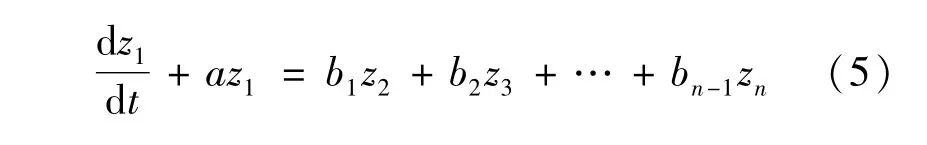
式中:a为膨胀系数;bi为灰色作用量。膨胀系数预测还原值的发展态势,灰作用量揭示序列数据的内在变化。在反射理论中,数据变化之间的关系是灰色的,没有确切的内涵。此外,灰色行为是内涵到外延的具体表现。它的存在是灰色模型与拓扑结构(黑箱理论)的分水岭,也是灰色系统观的重要标志[15]。
由此,序列数据的预测公式:
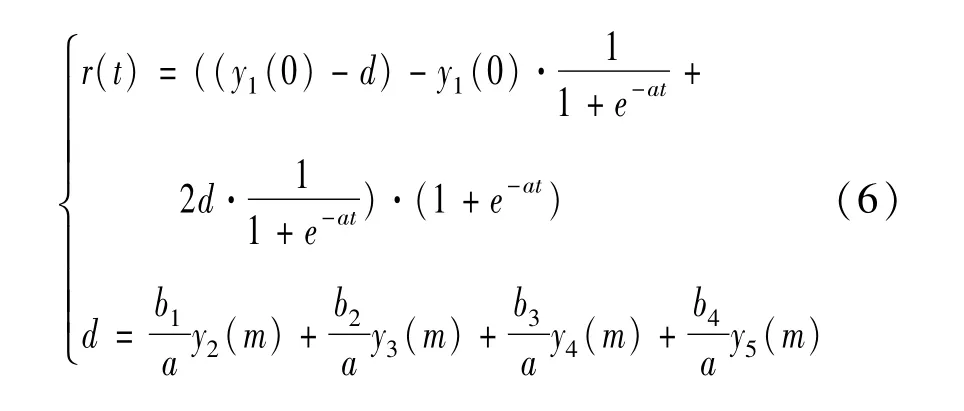
式中:r(t)代表TN预测值;yi为系统输入参数:y1为碳氮比(C/N);y2为碳磷比(C/P);y3为回流比;y4为有机负荷率;y5为投药量。
1.2 数据分析
试验样本取自2019年新疆某污水厂经Ⅱ期改造后的水样。据调查,I期出水含氮化合物的去除效果较差,因此Ⅱ期工程(深度处理-化学脱氮)主要以降低出水含氮化合物为研究。涉及项目涵盖水质基质化学需氧量(COD)、生化需氧量(BOD)、总氮(TN)、氨氮(NH+4-N)、总磷(TP)、投药比等。此外,以不易获取的关键参数C/N、C/P、有机负荷率(F/M)和投药剂量(聚丙烯酰胺(PAM)、聚合氯化铝(PAC)-4 h/次)为目标,均按5 d为循环周期,见表1。

表1 水质关键参数数据
基于MATLAB软件平台,利用带矢量微分的灰色神经网络子模块进行数据拟合和预测。本文中GM算法的参数设置如下:输入参数n=5,最大迭代次数为60,输出参数n=1。学习因子u1-6均取值在[0.001 5,0.003 5]之间。
图1为仿真结果,由图1(a)可知:前3个循环的实际去除率明显高于灰色神经网络预测值。同时随着迭代进化次数的增加,系统预测势态逐渐归一化,预测值高于实际值。与实际数据相比,GM算法所求解的势态更平缓,分布更均匀。从仿真结果图1(b)。可清晰地看出:尤其是针对相邻的小样本函数,GM算法在收敛性和分布性方面具有极大的优势。此外,灰色神经网络收敛迅速,但网络很快陷入局部最优状态,无法进一步修正参数[16]。

图1 灰色算法仿真结果曲线
相比而言,由表2中的数据可以看出:GM算法和实际数据的最大误差为7.31%,最小误差为0.42%。其次,网络预测的平均误差为4.46%,可见GM算法在解决小样本预测问题具有一定可行性。然而,误差值仍较大。与此同时,为提高GM算法的精确度,在保证约束粒子群算法(PSO)是可行解的条件下,对GM计算的原目标值进行较大程度上的改善,从而使其非线性规划均方差相对更小。

表2 GM算法和实际数据误差
2 优化模型
2.1 数据筛选
杨超[17]证实在GM算法建模数据具有较大误差限时,允许做不同的权衡,但数据必须等距、相邻、无跳跃。同时,在进行建模数据的选择时,以最新的实际数据为参照点,剔除旧数据,保持序列等维。此外,建模数据拟定后,为了获得最佳的拟合优度,使用SPSS统计学软件进行仿真验证,以确定关联度R2的值。若关联系数接近1时,表明互交效果良好[18],可作为参考。经过模拟验证,C/N、C/P、回流比和F/M的相关系数分别为0.893、0.493、0.532和0.316,而常量元素(PAM)的显著性不显著。因此,选取C/N、C/P、回流比和F/M作为约束粒子群优化的新参考点,以改善GM算法的极限误差。
2.2 建立模型
城市废水处理是复杂、滞后的生化过程,具有强耦合性、随机性、大时变、不确定性等特征。另外,出水水质机理模型的建模参数是固定的,无法适应废水处理工况条件的自适应变化。结合污水处理工况的动态特性,提出一种基于废水水质相关过程变量的自适应回归核函数,用于废水处理的水质参数模型。
粒子群算法(PSO)是一种新的仿生和随机搜索相耦合的并行算法。目前,PSO已成为优化适应度求解约束问题的研究热点,它基于个体自适应信息搜索,具有全局寻优能力。但PSO优化的最大缺点是易收敛到局部特定位置(而非局部极值)。褚丽娜[19]将非线性规划模型与标准粒子群算法有机结合,结果表明优化复杂问题是可行的。彭超达[20]基于单目标优化算法进行了实际应用讨论与研究,发现在无约束条件下样本出现失真。因此,对于单目标无约束优化问题,粒子群优化算法的优化效果所携带的信息就发挥不到应有的作用。进而,国内外学者在基于单目标粒子群算法上,对多目标粒子群算法(MOPSO)进行了广泛的研究,证明在求解全局优化多目标问题时MOPSO更实用有效。Song等[21]建立动态粒子群优化算法(DMS-PSO),结果表明:DMS-PSO方法能保证解集的良好收敛性和多样性。樊华羽等[22]引入α-stable分布理论,建立基于α-stable动态变异的多目标粒子群优化算法(ASMOPSO),结果验证了ASMOPSO算法的快速全局寻优性能,与Song等[21]结果类似。因此,本文在MOPSO算法的基础上,提出一种基于多目标约束粒子群耦合灰度模型(GM-MOPSO)的改进算法。该算法将出水TN浓度、出水BOD、R和随时间变化参数融合到多目标粒子群模型上,使得粒子群中的粒子更具多样性,收敛速度更快。同时,与MOPSO算法相比,该算法可以提高搜索最优解的效率,防止陷入极小值等优点,进而更大程度地降低模型计算所引起的误差。
根据污水处理厂运行过程的实测数据,生物脱氮时C/N为6.25∶1;生物除磷时C/P为99.5∶1。出水水质机理的物料守恒模型表达式如下,设
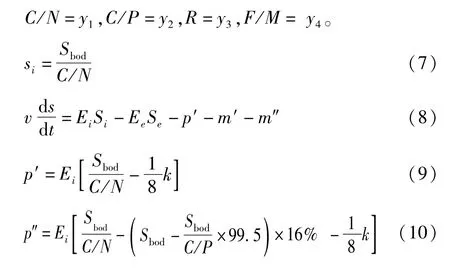

式中:Ei为输水流量,m3/d;Ee为出水流量,m3/d;Qs为出水水质,mg/L;Si为进水TN浓度,mg/L;Se为出水TN浓度,mg/L;p′为药剂脱氮的质量,g/d;p″为化学脱氮剩余的质量,g/d;m′为生物脱氮质量,g/d;m″为挥发的氮损的质量,g/d;Sbod为进水BOD浓度,mg/L;S′bod为出水BOD浓度,mg/L;S氨氮为进水氨氮质量,g/d;C/N为进水碳氮比;C/P为进水碳磷比;m为污泥排放量,t/(万m3);R为内回流比,%;K为药剂投放量,mg/L;S为污泥密度,mg/L;F/M为有机负荷,d-1;N为污泥含水率,%;V为反应池体积,m3。
通过分析式(7)~(12)可知:

优化目标函数为:
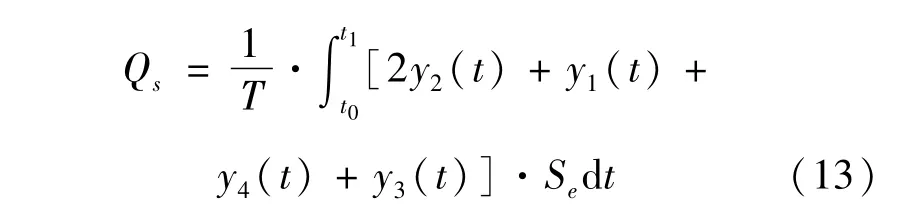
即:MinH(t)=[h1(t),h2(t),h3(t)]
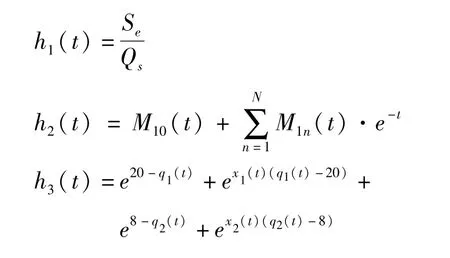
多目标约束条件:

式中:h1(t)、h2(t)、h3(t)均为多目标变量函数;Mn(t)为出水水质模型连接权值;q1为出水TN浓度;q2为出水NH+4-N浓度;xn(t)为t时刻水质基质函数输入。

2.3 优化结果及分析
2.3.1 GM-MOPSO算法流程
GM-MOPSO算法流程见图2。
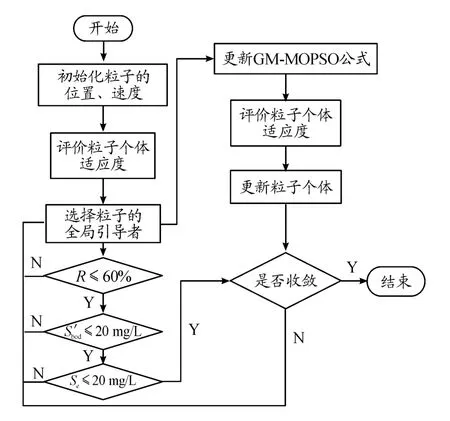
图2 GM-MOPSO算法流程框图
GM-MOPSO更新公式如下:

式中:o(J+1)为第(J+1)次迭代时的速度;r(J)为第J次迭代的位置;α1、α2为加速因子;X为全局收缩因子,加快GM-MOPSO算法的收敛速度;γ1、γ2为随机生成数;q(J)和s(J)分别为第J步迭代的个体最优和全局最优位置。
2.3.2 结果分析
采用GM-MOPSO算法进行优化,控制算法运行60步,能快速搜索到局部最优值,优化仿真结果如图3所示。
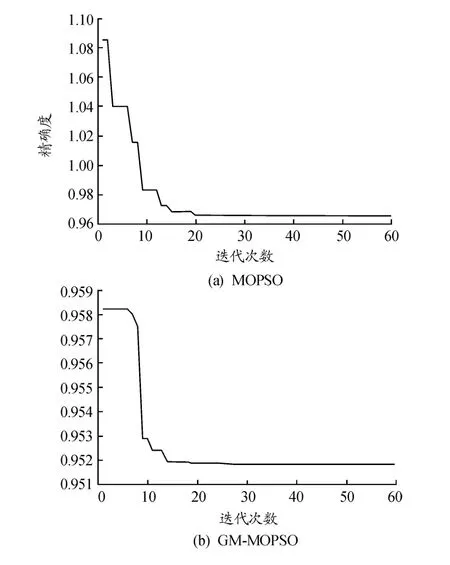
图3 优化仿真曲线
从图3可以看出:实际去除率的MOPSO迭代过程与GM-MOPSO模型迭代过程的收敛速度较缓慢,出现最优值点精度较低。同时,由图3(b)可知:GM-MOPSO模型最优值点的精度范围在[0.951 82,0.952 00],局部收敛的预测误差是12±0.2,预测误差较小。实验结果表明:多目标约束的GM-MOPSO函数模型能更好地预测出水TN输出值,且具有较高的精度。
由表3可知:对比MOPSO和GM-MOPSO 2种算法,GM-MOPSO算法的优越性明显,均方差相对更小,表明该算法稳定性更好,收敛性更佳。同时,约束条件下的最优变量取值分别为:C/N=7.30,C/P=80.00,F/M=0.10 d-1,回流比=54%,PAM=6 kg/h,而无约束的最优变量分别为:C/N=7.30±1,C/P=65.00±15,F/M=0.10±0.02 d-1,回流比=50.00±10%,PAM=6±1 kg/h。
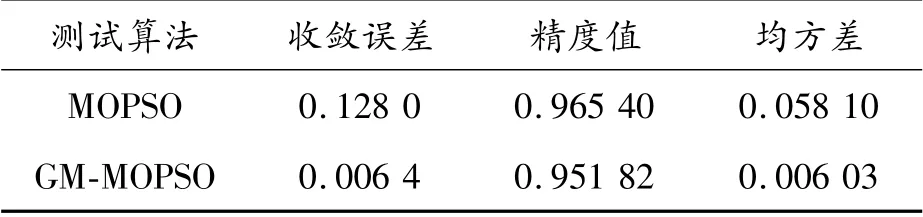
表3 不同算法收敛精度
2.4 响应面法验证
响应面法(response surface methodology,RSM)[23]是由英国学者Box和Wilson在1951年首次提出,并在此基础上开发的一套工具。它是将确定性“实验”拟合到响应面中来模拟实际极限状态面的一种将数学方法与统计方法相结合的技术,旨在确定实际工程应用中的最佳操作条件。因此,它通常用于对响应值受多个因素影响的问题进行建模和分析,从而达到优化响应值的目的。
根据约束条件下的最优变量值,结合RSM[24]原理,采用5因子1水平的Box-Behnken design(BBD)实验设计验证GM-MOPSO算法的准确性,以及探究工艺因素对脱氮的影响。同时,RSM的5个变量中C/N取6.30、7.30、8.30;C/P取50.00、65.00、80.00;F/M取0.08、0.10、0.12 d-1;混合药剂量(PAM-PAC)取5、6、7 kg/h;内回流比分别取40.00%、50.00%、60.00%。
如表4所示,5个因素,共产生46套数据,选取17套作为研究对象,进行验证水质参数的设计条件和运行数据。
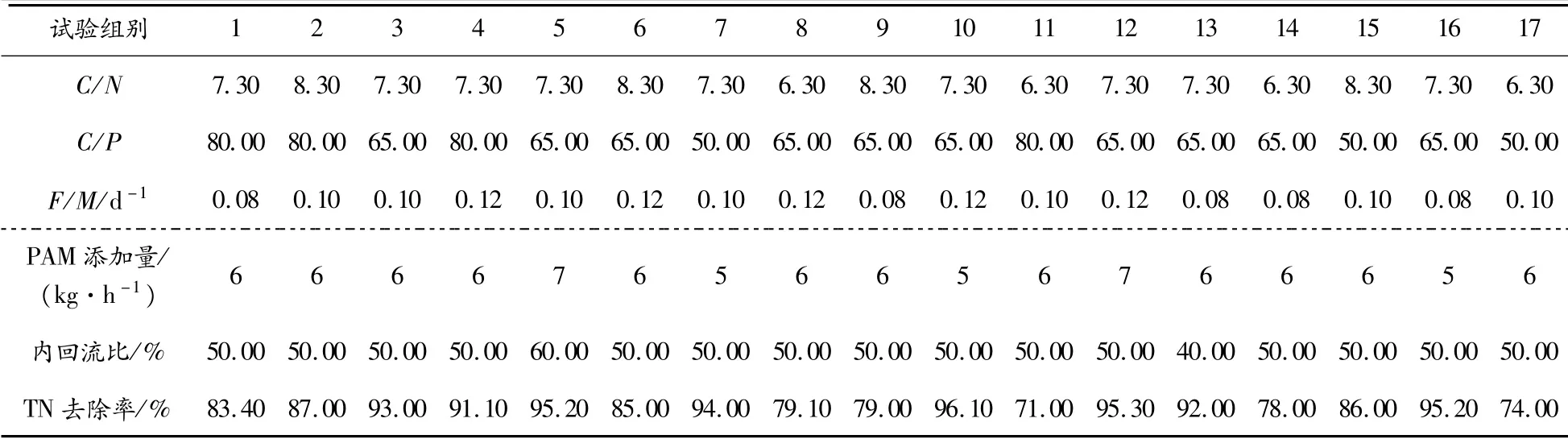
表4 水质参数的设计工况及运行数据
此外,去除率的二次回归预测方程,如式(16)所示:

根据回归方程分析,5个变量对TN的影响起主导性的是F/M。由图4可知:模型推测的试验结果能够直观反映变量之间交互作用的显著程度。因此,F/M与最优变量C/N、C/P、PAM-PAC、回流比之间交互作用显著。另外,由有机负荷和碳氮比的关系图(图4)表明:碳氮比与有机负荷交互作用对TN的去除效果影响较显著。在低有机负荷情况下,系统的脱氮效能不明显,随着提高C/N比和F/M的值,系统对TN去除明显提升,表明此时系统内部活性污泥处于增殖加速阶段,对有机物的降解能力最佳。陆佳等[25]在不同有机负荷条件下对好氧颗粒污泥的形成机制进行研究,表明高有机负荷更有助于促进细胞分泌胞外聚合物(EPS)。同时,刘小朋等[26]发现提高有机负荷不仅从根本上改变了污泥的形态,也显著增强了微生物活性。由此可见,F/M与C/N比的交互性促进去除率的增加。
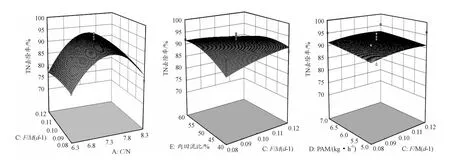
图4 F/M与最优变量交互图
其次,在显著性为0.05的显著水平(Fcrit)下,模型的失拟项呈现不显著(P=0.12>0.05)。当以F/M作为响应值时,模型的P值远小于0.01,表明回归方程的二次项模型显著水平良好,可用于模型推测试验的结果(图5)。经过验证,模型测试的试验结果与实际数据拟合良好。

图5 响应面结果验证图
从图5可知:响应面模型验证的GM-MOPSO算法最优结果为C/N=7.25,C/P=79.90,F/M=0.09 d-1,回流比=56.00%,PAM=7 kg/h与GMMOPSO模型实际数据相吻合。与此同时,响应面法TN去除率为96.57%,实际去除率为95.23%,GM-MOPSO算法对TN去除率为95.18%,三者误差分别为-1.370%和0.048%。结果表明:GMMOPSO求解算法的指标数量级差异更小,在求解约束多目标问题时是可行和有效的。经比较分析,虽然PAM投加量有所增加,但估算的运营成本表明,增加的成本降低了微生物分泌物对系统的二次污染。
综上所述,水质参数F/M和约束条件都会影响系统的性能。但是目前二者没有统一的公式描述其变化的范围和规律。根据仿真结果可知,GMMOPSO算法的结果对水质参数较为敏感,该参数不仅影响最终非支配解集的规模,同时也会在一定程度上影响解集的多样性和分布性能。
2.5 污水厂实际模型控制分析
通过实际污水处理厂在线监控功能对进水口C/N、C/P、F/M等多目标控制进行调整,以验证GM-MOPSO算法可靠度,如表5所示。

表5 实际模型控制运行数据
经验证,该模型的精度与实际污水厂运行控制的实测数据结果相吻合。结果表明:本文提出的优化方法是可靠的、准确的、有效的。
3 结论
1)通过GM算法分析,数学模型对TN预测值和实际数据的最大误差和最小误差分别为7.31%和0.42%,相对误差在[0.005 9,0.110 0](%)之间,误差值也有较大差异。结果表明:GM算法优化脱氮工艺具有一定的实践指导意义,但也存在不足。此外,运用该模型能够预测脱氮在实际运行时的大致变化。
2)对GM模型优化后,运用耦合GM-MOPSO算法建立了多目标约束,通过非线性关系准确地反映多目标约束之间的映射关系,从而得到了最优变量条件。因此,最佳变量参数分别为:C/N=7.30,C/P=80.00,F/M=0.10 d-1,回流比=54.00%,PAM=6 kg/h,在此工艺条件下,系统对TN去除率为95.18%,有利于系统的脱氮。
3)结合响应面法验证耦合GM-MOPSO模型准确性表明,对TN的影响起主导作用的是F/M。同时,测试的最优结果为C/N=7.25,C/P=79.90,F/M=0.09 d-1,回流比=56.00%,PAM=7 kg/h与GM-MOPSO模型实际数据相吻合,且相对误差更小,说明多目标约束的GM-MOPSO函数模型能较好地预测出水TN输出值,并具有较高的精度。
4)经过预测算法模型可靠性后,通过污水处理厂的在线监测功能实现进水口C/N、C/P、F/M等多目标的控制,达到了与算法等效的功能。

