基于优化概率密度函数的图像对比增强技术研究

惠学武

（中国人民解放军海军大连舰艇学院，辽宁 大连 116018）

图像采集设备获取的某些辨识度较低的图像，严重制约计算机视觉识别系统的识别效果。图像增强技术可以增强图像的对比度，提高图像的视觉质量，促进肉眼或计算机对图像的识别，已经广泛应用在多个领域［1］。直方图均衡化HE（histogram equalization）是增强图像对比度的常用空间域方法，通过将直方图变换为具有均匀密度分布的直方图，然后再按照直方图调整原有图像以增强图像对比效果，无需设置参数就可以有效地增加图像的对比度［2］。但是，鉴于直方图均衡化只是改变原图像中同一灰度层上所有像素的灰度，导致均衡化图像的动态范围扩大，不可避免存在灰度吞噬现象、最亮的像素点过于饱和、结构信息丢失，图像过度增强的情况［2－3］。

为了解决这些问题，学者提出了多种优化直方图均衡化的方法。Kim［4］提出了保持亮度的双直方图均衡BBHE（brightness preserving bi-histogram equalization），根据原图亮度的均值将原图划分为2个图像，然后独立对每个直方图进行均衡化。江巨浪等［5］针对传统的双直方图均衡算法不能精确实现图像亮度保持目标的问题，提出了一种新的双直方图均衡算法。Sim等［6］利用图像均值将原图划分为2个子图像，然后利用子图像的均值划分子图像，提出递归子图像直方图均衡化RSIHE（recursive sub-image histogram equalization）。但是该方法迭代次数最优值的选择较为困难，递归次数较大时图像的增强效果会严重退化。Mary等［7］发展了递归分离加权直方图均衡均值RSWHE-M（recursive separated and weighted histogram equalization me）。Singh等［8］提出曝光的子图像直方图均衡化ESIHE（exposure-based sub-image histogram equalization）可以很好地增强原图的对比度，但是无法确保图像的亮度。Ooi等［9］提出平台受限的双边直方图均衡BHEPL（bi-histogram equalization with a plateau limit）。Jingrui等［10］提出基于强度曝光的双直方图均衡化IEBHE（intensity exposure-based bi-histogram equalization）直方图，但有时该方法会出现图像对比度不强的情况。Seonhee等［11］基于变分优化的retinex模型LLVORM（low-light image enhancement using variational optimization-based retinex model）增强低亮度图像对比度。Jingrui等［12］根据图像中值亮度分割直方图，得到改进的双直方图均衡化方法BHEMHB（bi-histogram equalization using modified histogram bin）。李艳萍等［13］提出了基于限峰分离模糊直方图均衡化的图像增强算法。罗强等［14］针对偏暗、低对比度图像视觉显著性图提取效果不理想的问题，提出一种基于改进的直方图均衡化的图像显著性图提取算法。

大多数自适应直方图均衡化方法都是局部增强，针对该方法在增强图像对比度时会出现平均亮度不足、图像过度增强、失真等问题，本文基于图像强度的期望值E［Ik］（the expected value of image intensity），构建全局自适应的图像概率密度函数（an global adaptive probability density function），最后使用累积分布函数（cumulative distribution function，CDF）转换得到重建的图像，以保证总体直方图具有熵最大性质，抑制过度增强，得到最适中图像的增强。

1 算法设计

提出的优化方法流程如图1所示，鉴于直方图均衡化算法可能导致过度增加图像强度的情况，本文首先选用裁剪阈值的方法裁剪图像直方图，然后生成相应的图像概率密度函数PDF，根据图像强度期望值E［Ik］和绝对平均误差（average absolute error metric）得到全局自适应的图像概率密度函数，经过转换函数后重新构建图像，最终输出处理后的图像。

图1 图像处理流程框图

1.1 裁剪图像直方图

假设灰度图像I的图像强度为I0，I1…IL－1，直方图为H（Ik）。生成图像的直方图后，如式（1），选择图像直方图中图像强度值的中位数作为裁剪阈值，裁剪图像直方图。

式中：n（i）是图像直方图的灰度级数。

那么，裁剪后的图像直方图HC（Ik）表示为：

1.2 直方图概率密度函数的优化

得到裁剪图像直方图后，根据式（3）图像直方图的概率密度函数得到不同图像强度下的图像直方图的概率密度值。

式中：k为图像的强度水平；M×N是图像中的像素总数。然后，在考虑图像强度期望值E［Ik］和平均绝对误差的基础上对其进行优化。

1）图像强度期望值E［Ik］

当采用直方图均衡化的时候，图像强度值E［Ik］会根据图像的平均亮度而变化，对于低亮度的图像其E［Ik］较小，高亮度的图像E［Ik］则较高，即在某种意义上E［Ik］具有自适应性。另外，期望值E［Ik］也会直接影响增强图像的处理效果。所以本文利用E［Ik］的自适应性，通过调整E［Ik］值来优化图像直方图概率密度函数，提高图像的对比度，E［Ik］的计算如式（4）所示。

式中：L为图像强度等级的总数；max（Ik）为图像的最大强度值。下文将分析E［Ik］值对图像效果的影响。

2）平均绝对误差

另外，本文选择平均绝对误差来优化概率密度函数，定义误差为2个不同强度下概率密度函数PDF之间的差。计算平均绝对误差的具体过程为：

步骤1令图像的PDF为1×L的行矩阵，其中P0，P1…PL－1为特定灰度下的概率密度值。

步骤2将PDF分为2个子集：PDF1和PDF2，PDF1的范围为P0～Pi；PDF2为Pi＋1～PL－1。

步骤3设PDF1和PDF2的平均值为PDF1avg和PDF2avg。

步骤4生成大小分别为PDF1和PDF2的2个单位矩阵I1和I2。

步骤5将PDF1avg与I1相乘，PDF2avg与I2相乘得到矩阵M1和M2，M1和M2组成1×L的行矩阵M。

步骤6得到PDF矩阵和M矩阵的绝对差矩阵Di，得到矩阵Di的平均值矩阵Dim。

步骤7从步骤2开始计算从i＝0到255的所有强度值每次迭代得到对应的Dim值，计算完成后得到由Dim值组成的矩阵F。

通过式（5）对F进行归一化：

得到平均绝对误差如下：

最后，在考虑图像强度期望值和平均绝对误差的基础上，根据图像强度值递归分割图像的PDF，得到优化图像直方图概率密度函数PDFm（Ik）为：

1.3 基于分布密度函数变换的图像重建

在得到优化的概率密度函数PDFm（Ik）后，根据式（8）计算分布函数CDF（cumulative distribution function），再根据式（9）转换函数获得增强后的图像。

转换函数为：

1.4 E［Ik］值对图像对比度的影响

为了分析E［Ik］对增强图像对比度效果的影响，选取战斗机图像进行分析，如图2所示，曲线是取不同E［Ik］值时得到优化后的PDF与图像灰度大小的关系，对应处理后的图像如图3所示。通过图2可以看出E［Ik］对PDF曲线的变化影响较为明显，可以分为E［Ik］值较大和较小时2种情况讨论影响的结果。

图2 不同E［Ik］值下战斗机图像的PDF曲线

图3 不同E［Ik］值下战斗机的增强图像

1）E［Ik］值较小

如图2所示，当E［Ik］值为0.001时，图像的PDF曲线与原始曲线重叠；当E［Ik］值为0.1时，它与原始曲线的变化趋势基本一致，PDF值略小于原有值。

因此，当E［Ik］的值小于等于0.1时，可以忽略式（7）中的因子E［Ik］*e，将式（7）转换为：

另外，由于

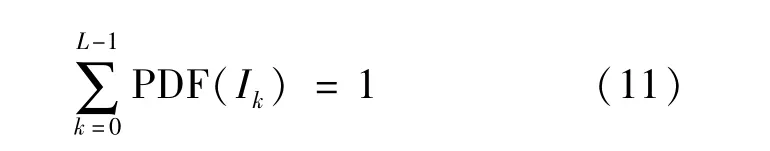
因此，优化后的PDF等于原有的PDF，即：

如图3所示，增强后的图像图3（d）与原有的直方图均衡化图像几乎没有差别，图3（e）与原有直方图仅有略微的差别。

2）E［Ik］值较大

从图2可以看出，当E［Ik］为100时，生成的PDF曲线的波动很小，没有明显的波峰和波谷。因此，当选择E［Ik］值大于等于100时，可将式（6）转换为：

如图3所示，当E［Ik］＝100时，图像增强后的效果类似于原始图像。取E［Ik］＝0.77得到优化的PDF曲线，如图2中的黑色实线所示，相比于原有的PDF曲线，优化后的曲线增大了原始PDF的最小值，降低了最大值，起到了“削峰填谷”的作用。同时，从主观上看图3（c）图像的增强效果是所有E［Ik］值中最好的。

2 实验结果与分析

将本文的方法应用于多个灰度图片，并与HE、BBHE、IEBHE、LLVORM、BHEPL、BHEMHB技术比较。测试图像取自标准计算机视觉组（CVGUGR）数据库和柯达无损真彩色图像套件。

2.1 客观评价

2.1.1 客观评价指标

常用的图像质量客观评价指标有：熵［15］（image entropy）、峰值信噪比［16］（peak signal to noise ratio，PSNR）、梯度幅度相似性偏差［17］（gradient magnitude similarity deviation，GMSD）、直方图利用率［18］（histogram utilisation efficiency，UEh）、结构相似度（structural similarity index，SSIM）、平均梯度［19－20］（average gradient，AG）等。其中，结构相似度可度量2幅图像的相似程度，广泛的用于图像的去噪和复原中，不宜通过对比2幅图像的相似程度评价增强效果的好坏，故不采用该方法。由于图像的熵和平均梯度均属于无参考质量评价且都反映图像的信息量，可以选择其中一个指标评价图像增强效果。所以，为了定量比较本方法增强图像的效果，本研究选择以下4种评价指标：

①熵是衡量图像直方图中均匀分布的情况，可以预测图像细节的丰富性，熵的定义如下：

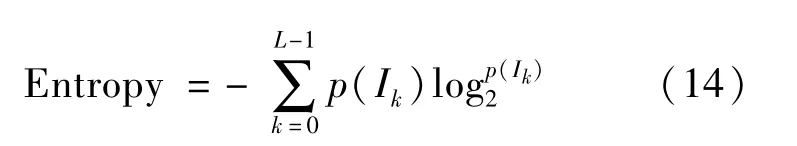
式中：p（Ik）是强度级别k的概率值；L为图像强度等级的总数，图像的动态范围为［0，L－1］。熵的值越高，表示图像的信息量越大，细节越丰富。所以，理论上得到处理后图像的熵值越大越好。

②峰值信噪比PSNR主要用于计算输入图像和处理图像之间的质量增益，可以表征图像是否保持自然外观，PSNR的计算如式（15）所示。

式中：MSE（mean square error）是当前图像X和参考图像Y均方误差；H、W分别为图像的高度和宽度；t为每个像素的比特数，取8；PSNR单位为dB，其值越高代表图像失真越少。

③梯度幅度相似性偏差GMSD可以表征图像的扭曲程度，GMSD的值越小图像的质量越高。GMSD的数学计算如下：

式中：Y×Z是图像I的大小。

④直方图利用率UEh是另一个图像直方图的主要属性。对于一个对比度较好的图像，在不过多改变图像直方图的主要特征的情况下，图像的直方图尽可能的规则地散布在整个区域之内，UEh表示为：

式中：NBe和NBO为增强图像和原始图像的非零像素数目。由于增强图像中的非零像素数目比原始图像中的非零像素数目要少，因此UEh的值小于1。但是，如果该值远小于1则会破坏图像质量。所以，该值越接近于1图像的质量越好。

2.1.2 客观评价结果分析

利用不同的方法得到各种测试图像的客观评价结果如表1～4所示，将表中最优的2个值加粗显示。

表1 信息熵评价指标

由表1可知，与其他方法相比，本文的方法处理不同图像后得到的的熵值最高，熵的平均值为6.75也最接近输入图像的6.774。因此，该方法体现图像中的大部分的信息，很好地体现图像的细节。

由表2中的PSNR值可知，与其他方法相比，本方法处理战斗机、长发和短发女士图像后得到PSNR的最大值，处理其余图像得到的PSNR值相对不是最大值，但本方法得到PSNR值的平均值最大。这表明本文的方法的鲁棒性较好，可保持不同类型图像的质量，适用于不同类型的图像。

表2 峰值信噪比PSNR

从表3可知，本方法处理除爱因斯坦图像外所有图像的GMSD值是所有方法最小的，且总的平均值明显小于其他算法的均值，说明本方法可以在失真非常小的情况下增强图像的对比度。

表3 梯度幅度相似性偏差GMSD

从表4可以看出，相比于其他方法，本方法处理除爱因斯坦图像外所有图像后得到的UEh值都是最高，平均值最大且明显高于大部分方法，说明方法在增强对比度的同时保持了图像基本特征。

表4 直方图利用率UEh

2.2 主观评价

为了验证本文方法的效果，本节采用主观的视觉评估方法，由于篇幅限制分别选取2组黑白图像图4、5，2组彩色图像图6、7进行增强效果的对比和分析，实验结果如图4～7所示。

图4 爱因斯坦图像的增强

图6 短发女士图像的增强

图4显示了7种方法处理爱因斯坦图像的结果。其中，HE和BBHE方法过度增强了图片的亮度，图像发黑，失真较为明显。BHEPL方法导致了图像模糊，略有些过亮。MMBEBHE方法在增强图像后导致图像失真。IEBHE和LLVORM方法增强图像对比度的效果较好。虽然BHEMHB方法增强了图像，但不是很平滑。相比较而言，本文的方法处理图像后视野相对清晰，增强效果较好。

图5显示了长发女士图像的结果。采用HE、BBHE方法增强图像后出现几乎相同的过度增强效果。IEBHE方法处理后图像亮度整体较暗。BHEPL处理后的图像有些失真。LLVORM和BHEMHB方法在增强图像对比度的同时也很好地保持了图像的原有特点。本文的方法增强效果略好于LLVORM和BHEMHB方法且图像较为自然。

图5 长发女士图像的增强

图6显示了7种算法对短发女士彩色图像处理的结果，可以清楚地看到，经HE和BBHE处理后的图像出现了一定程度的扭曲和噪声，图像失真严重。IEBHE生成的图像亮度太高。BHEPL方法的增强效果较好。LLVORM和BHEMHB增强了图像的对比度，但扭曲了图像的颜色。本文的方法很好地增强了短发女士的对比度，很好地保留了图像的细节，但图像的背景较暗，整体来看处理效果较好。

图7显示了各方法处理窗子图像的结果。原图的亮度较为暗淡，经过HE、BBHE和BHEPL方法处理后，图像变得明亮且清楚，但都丢失了原图的某些自然特征，有些失真。IEBHE、LLVORM和BHEMHB方法过度增强了图像的亮度。本文方法在保留原有图像自然的外观的同时很好地增强了图像的对比度。

图7 窗子图像的增强

由上述对比结果可以得出，本文提出的改进算法增强强度适当，没有出现由于过度增强而发黑的现象，由图4、6可以看出，本文算法的细节保持能力更强，相比于其他的方法处理黑白和彩色图像的能力都能更胜一筹，说明适用的范围更广。

3 结论

为了改进目前直方图均衡化局部增强方法的不足，基于图像强度的期望值，构建了全局自适应的图像概率密度函数，提出了一种新的图像对比度增强技术，改进了目前直方图均衡化在增强图像对比度方面的不足。对比实验证实了本文方法能有效解决其他直方图技术中存在图像失真、对比增强效果不好等问题，在熵值、峰值信噪比、梯度幅度相似性偏差和直方图利用率方面优于其他方法，主观上也显示其鲁棒性优于现有的方法。