平面磁场式绝对角度传感器的误差产生机理与抑制方法研究

高文政，石 洪，汤其富

（1.连云港杰瑞电子有限公司，江苏 连云港 222061；2.重庆理工大学 机械检测技术与装备教育部工程研究中心，重庆 400054）

基于PCB工艺的平面磁场式传感器属于电磁感应类传感器［1］，具有较强的抗干扰、抗冲击和振动能力，不惧油污、水汽、粉尘、盐雾等影响。与传统的电磁感应式传感器等一样，如旋转变压器、感应同步器、LVDT、RVDT、电涡流传感器［2－7］，该类传感器可应用于工业、航空航天、国防等工作环境比较恶劣的领域。由于PCB工艺在角度传感器中的应用优势，PCB型平面式角度和直线传感器得到迅速发展［8－16］。例如：以色列Netzer公司的角度传感器和文献［8］描述的传感器基于电容传感技术设计，采用PCB工艺制造定子和转子的传感电容极片；英国Zettlex公司的IncOder系列角度和直线传感器，基于电磁感应原理设计，采用PCB工艺制造定子／直线尺和转子／测头的平面线圈；瑞士Posic公司的平面式角度和直线传感器，以及文献［10］描述的传感器，也是基于电磁感应原理设计，采用PCB工艺制造角度传感器的转子和直线传感器的动尺；中国广东盈动高科自动化有限公司的无轴承角度传感器，采用的传感原理与Netzer公司产品类似，也采用PCB工艺制造定子和转子的传感电容极片。

PCB技术和工艺可以实现复杂线圈和极片的制造［8，11］，为厚度小的平面式传感器提供了便利，所以近年来无人机、机器人、安防设备、伺服电机等大量采用基于PCB工艺的传感器。不过，采用PCB工艺的电容式和电磁感应式传感器在测量精度方面，尤其是电磁感应式传感器，与光电式传感器有一定差距。

基于汤其富［17］的研究，开展了平面磁场式绝对角度传感器的误差产生机理及抑制方法研究。由于电磁感应式角度传感器的短周期误差通常比较明显，且具有较强规律性［11，14－15］，因而减小短周期误差是一条提高测量精度的有效途径。通过研究传感器的常见短周期误差产生机理，从传感器信号处理层面对短周期误差进行抑制，达到提高传感器测量精度的目的。

1 传感器的传感结构与工作原理

1.1 传感器的传感结构

文献［17］中所描述的传感器，属于一种电磁感应式角度传感器。在对该传感器的研究中，为了扩展磁场的分布区域并提高其密度，为定子增加了内外环2组环形线圈，与原环形线圈串联，得到如图1所示的传感器结构，也为传感PCB的布线图，PCB中包括2个传感通道：内环正弦形线圈与中间环、内环2组环形线圈组成1个传感通道；外环正弦形线圈与中间环、外环2组环形线圈组成另外1个传感通道。内外环正弦形线圈的周期数相差为1，且各包括空间上正交（即空间上相差1／4正弦周期）的2组线圈［17］，称为SIN线圈和COS线圈，使2个传感通道组合可以实现绝对式测量。该传感器可以采用基于鉴相和鉴幅原理的2种信号处理方法。如果采用鉴相式信号处理方法进行位移解算［15，18－19］，则正弦形线圈作为励磁线圈、环形线圈作为感应线圈。正弦形线圈的SIN线圈和COS线圈中通入两相时间上正交的交变信号，则环形线圈通过与正弦形线圈的电感耦合而接收磁场。转子上的铜箔阵列在旋转时，则周期性地改变环形线圈与正弦形线圈的耦合系数，使环形线圈输出相位周期性变化的正弦信号；如果采用鉴幅式信号处理方法进行位移解算［20－21］，则环形线圈作为励磁线圈、正弦形线圈作为感应线圈。在环形线圈中通入交变信号时，则正弦形线圈通过与环形线圈的电感耦合而接收磁场。转子上的铜箔阵列在旋转时，则周期性地改变正弦形线圈与环形线圈的耦合系数，使正弦形线圈输出幅值周期性变化的正弦信号。

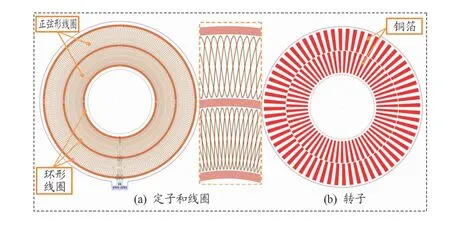
图1 传感器的传感结构图（PCB布线图）

1.2 传感器的基本工作原理

当采用鉴相式信号处理方法进行位移解算时，内外环的正弦线圈不可同时通入交变信号，而是分时通入。设内外环正弦形线圈的周期数分别为N和N＋1，通入正弦线圈的SIN线圈和COS线圈的交变信号分别为U1（t）＝Umsin（ωt）和U2（t）＝Umcos（ωt），其中t表示时间，Um表示信号的幅值，ω表示信号的角速度。传感器每次上电后，首先将交变信号通入内环线圈，则环形线圈输出式（1）所示的信号。然后，再将交变信号通入外环线圈，则环形线圈输出式（2）所示的信号。依照文献［15］介绍的方法对2种信号进行组合处理，得到初始绝对角位置。初始绝对角位置得到以后，交变信号保持通入外环线圈，使传感器由式（2）信号获取增量角位移，而新的绝对角位置通过在初始绝对角位置上累加增量角位移得到。

式中：kN、kN＋1表示与传感器相关的常数系数；θ表示被测角度。

当采用鉴幅式信号处理方法进行位移解算时，设通入环形线圈中的交变信号为U（t）＝Umsin（ωt），则内环SIN线圈和COS线圈输出的信号如式（3）（4）所示，外环SIN线圈和COS线圈输出的信号如式（5）（6）所示。将该4路信号分别进行幅值解调、模数转换、求反正切等操作，得到对应于内外环的2种角度信息，再依照文献［15］介绍的方法对2种信号进行组合处理，得到绝对角位置。

式中：k1和k2表示与传感器相关的常数系数。

PCB型电磁感应式传感器的线圈数量往往较少，通常只有1匝或几匝，不适合采用基于鉴相原理的信号处理方法，因为该方法往往只允许传感器工作于20 kHz及以下频率，传感器不易在较小功耗情况下输出较强的感应信号。基于鉴幅原理的信号处理方法允许传感器工作于数百kHz至数MHz［9－10，12－13］，可以在较小功耗情况下输出较强的感应信号。另外，鉴幅式信号处理方法具有较好的灵活性，可以在信号处理层面弥补感应线圈输出信号的不足，抑制传感器的短周期误差。再者，对于图1所示传感器，与鉴相式信号处理方法相比，鉴幅式信号处理方法可以同时根据内外环信号进行组合求解绝对角位置，而不必采用分时方式。因此，本文所研究的角度传感器选用了鉴幅式信号处理方法。

2 传感器的信号处理方法概述

传感器采用的信号处理方法如图2所示，图中描述了该方法的基本硬件架构和工作原理。传感器的基本硬件包括激励电路、解调电路、模数转换电路和主控电路。激励电路为励磁线圈提供交变信号；解调电路从调幅波中解调出反映位移的正余弦信号；模数转换电路将正余弦信号转化为主控电路可以识别的数字信号；基于FPGA的主控电路控制激励电路、解调电路和模数转换电路，并根据得到的正余弦数据运算得到并输出角度信息。

图2 传感器的鉴幅式信号处理方法基本硬件架构和工作原理示意图

解调电路由混频电路和低通、放大电路组成。式（3）～（6）所示信号经过混频电路时，如果只考虑解调方波的基波，且设VCOM＝0、基波幅值为1，基波相位与调幅波的载波相同，则得到混频后的信号如式（7）～（10）所示。

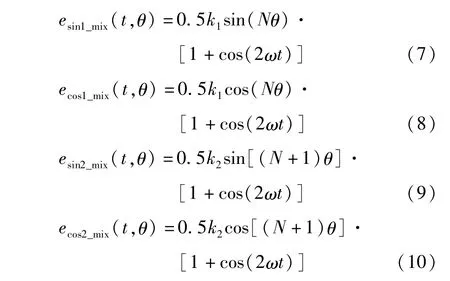
混频后的信号经过低通滤波、放大电路后，高频成分（频率为励磁信号的2倍，即cos（2ωt）形式的成分）被大幅衰减、低频成分（反映位移的正余弦信号）被放大。假定低通滤波、放大电路为理想电路，则滤波和放大后的信号可由式（11）～（14）表示。低频成分由模数转换电路转化为数字量，再经过FPGA进行反正切解算等数字信号处理，最终得到被测角度θ。

3 传感器的短周期误差产生机理

由于传感器的内外环线圈仅是正弦周期数不同，所以本部分将以N周期的感应线圈为例，对传感器的常见短周期1次和2次误差的产生机理进行阐述。

3.1 短周期1次误差

传感器在理想状况下，当转子不参与工作时，感应线圈输出的信号强度应该为零，因为励磁线圈的环形结构和正弦形感应线圈的对称结构使励磁线圈产生的磁场在感应线圈中得以完全抵消。然而，由于传感器的制造、安装、引线等环节的实现难以达到理想状况，导致感应线圈不能完全抵消无转子时的磁场，所以即使转子不参与工作，感应线圈中仍会产生少许感应电动势。该电动势与转子角度无关，可称之为无效电动势。因此，传感器在正常工作情况下，无效电动势使感应线圈输出的信号中包含了与转子角度不相关的成分，则信号的表达式应在式（3）（4）基础上变为式（15）（16）。其中，k11和k12表示与无效感应电动势相关的常数系数。

式（15）和（16）所示信号经过混频、低通、放大电路后，虽然高频成分被滤除，但剩余信号除了低频成分外，还包含直流成分，表达式如（17）和（18）所示。

与式（11）（12）相比，式（17）（18）中的直流成分在位移解算时将引入误差。例如，以式（17）（18）求解θ，并设误差为δ1，则θ、δ1与式（17）（18）具有如式（19）的关系。

由式（19）可得：

通常情况下，k′11和k′12远小于k′1，所以式（20）可以简化为：

一般情况下，δ1的值比较小，所以δ1≈tanδ1。式（21）表明，θ变化360°，δ变化N个周期，即与感应线圈的正弦周期数相同。因此，当传感器的制造、安装、引线等环节不理想时，如果导致感应线圈在转子不参与工作时的感应电动势不为零，则测量时产生短周期1次误差。

3.2 短周期2次误差

根据传感器的测量原理可知，感应线圈的两路输出信号在经过模数转换电路后，应当幅值相等、相位相差90°。然而，无论传感器的制造、安装、引线等环节，或者信号处理环节，都有可能导致两路信号经过模数转换电路后存在幅值不相等或相位差不为90°的问题。如此问题亦会在测量中引入误差。

首先，考虑两路信号经过模数转换电路后幅值不相等的情况。假定两路信号如式（22）（23）所示，即二者的幅值相差Δk′1。

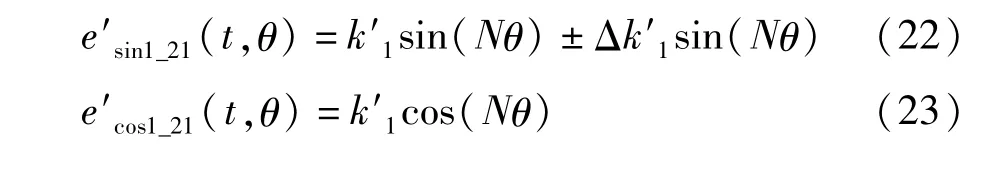
设误差为δ2＿1，则θ、δ2＿1与式（22）（23）具有如式（24）的关系。

由式（24）可得：

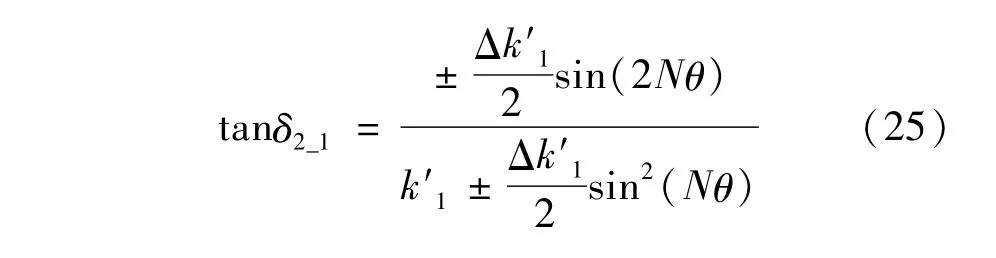
通常情况下，Δk′1也远小于k′1，所以式（25）可以简化为：

其次，考虑两路信号经过模数转换电路后相位差不为90°的情况。假定两路信号如式（27）（28）所示，即二者的相位差为（90°±φ）。

设误差为δ2＿2，则θ、δ2＿2与式（27）（28）具有如式（29）的关系。

由式（29）可得：

通常情况下φ的值比较小，从而sin2（θ±φ／4）sin2（φ／4）≈0、cos2（＋sinθsin（θ±φ）≈1，所以式（30）可以简化为：

一般情况下，δ2＿1和δ2＿2（的值也比较小，所以δ2＿1≈tanδ2＿1、δ2＿2≈tanδ2＿2。根据式（26）和（31）可知，θ变化360°，δ2＿1和δ2＿2均变化2N个周期，即是感应线圈的正弦周期数的2倍。因此，当传感器的制造、安装、引线、信号处理等环节不理想时，如果导致输入模数转换电路的信号幅值不相等或相位差不为90°，则测量时产生短周期2次误差。

4 传感器样机的误差测试实验

4.1 样机与测试平台

实验所用的样机如图3（a）所示，其定子PCB内外环的正弦周期数分别为63和64。为了提高励磁线圈与感应线圈的耦合系数，使传感器输出较强的信号，定子PCB和转子PCB均贴于导磁基体之上。同时，导磁基体为PCB的平面度提供了支撑。测试平台如图3（b）所示，主要由待测传感器样机、数据采集及处理电路、高精度光栅（HEIDENHAIN RON886，精度为±1″）、数控转台、大理石基架等几部分组成。待测样机与光栅同轴安装，在转台的带动下二者的转子同步旋转，测量数据由数据采集电路同步获取。

图3 传感器样机和测试平台照片

4.2 初始实验和结果

实验以图3中所示的光栅作为测量基准，对样机的63周期内环通道和64周期外环通道分别进行了整周（0°～360°）和短周期（0°～5.7°，0°～5.625°，其中，5.7°≈360°／63，5.625°＝360°／64）误差测试，即下述测量误差均表示与基准光栅比较测试所得，且所述误差均为原始测量误差。

在该传感器的前期研究中，采用了基于鉴相原理的信号处理方法，励磁信号的频率通常不高于20 kHz，导致传感器定、转子的工作间隙很小时（0.2 mm）方可得到高信噪比的信号［15］，所以对安装条件的要求较为苛刻。本文的研究将传感器样机的励磁信号频率提高到了125 kHz，使其可工作于1 mm的间隙。样机在1 mm工作间隙下进行了初步测试，短周期和整周误差曲线分别如图4～7所示。63周期内环通道的短周期误差为－70.9″～16.3″（峰－峰值87.2″），整周误差为－92.9″～17.6″（峰－峰值110.5″）；64周期外环通道的短周期误差为－2.5″～54.2″（峰－峰值56.7″），整周误差为－4.7″～60.7″（峰－峰值65.4″）。从图4、6可以看出，2个通道存在明显的短周期1次误差。

图4 63周期内环通道的短周期误差（初测）曲线

图5 63周期内环通道的整周误差（初测）曲线

图6 64周期外环通道的短周期误差（初测）曲线

图7 64周期外环通道的整周误差（初测）曲线

4.3 短周期1次和2次误差的抑制及实验结果

根据前文对短周期1次误差产生机理的分析，为了该频次的误差，则需要减小感应线圈中无效电动势的影响。由于该影响在信号处理过程中表现为式（17）（18）中直流成分k′11和k′12的影响，所以在求反正切过程中补偿直流成分是抑制短周期1次误差的一条途径。采用的具体方法为：样机上电后移去转子，即转子不参与工作，然后获取并记忆模数转换后的值，即k′11和k′12的值；样机正常工作时，将进行反正切运算的分子和分母分别减去所记忆的k′11和k′12值，从而减小或消除无效电动势的影响。

采取了上述抑制短周期1次误差的方法后，63周期内环通道的短周期误差峰－峰值减小了约55%，64周期外环通道的短周期误差峰－峰值减小了约45%，从而2个通道的整周误差也随之减小，短周期和整周测量误差曲线分别如图8～11所示。63周期内环通道的短周期误差为－24.5″～14.7″（峰－峰值39.2″），整周误差为－49.4″～20.8″（峰－峰值70.2″）；64周期外环通道的短周期误差为－13.9″～17″（峰－峰值30.9″），整周误差为－10.3″～30.3″（峰－峰值40.6″）。因此，无论是短周期误差还是整周误差，均表明抑制方法具有显著效果。

图8 63周期内环通道的短周期误差曲线（抑制1次误差后）

图10 64周期外环通道的短周期误差曲线（抑制1次误差后）

图11 64周期外环通道的整周误差曲线（抑制1次误差后）

图8、10显示，63周期内环通道的短周期误差仍是1次为主，而64周期外环通道的短周期误差表现出明显的2次成分。由于内环通道在实际工作中仅用作绝对位置判断的辅助通道，其误差只要满足绝对位置判断的要求即可。对于63和64周期的2个通道，二者的误差之差不大于160.7″（160.7″≈（1 296 000″／63／64／2，360°＝1 296 000″）时，便可进行准确的绝对位置判断。将图9、11对应的误差数据做差，得到的曲线如图12所示，最大值为59.8″，显示已经远远满足绝对位置判断要求。因此，对内环通道的误差便没有采取进一步抑制措施。

图9 63周期内环通道的整周误差曲线（抑制1次误差后）

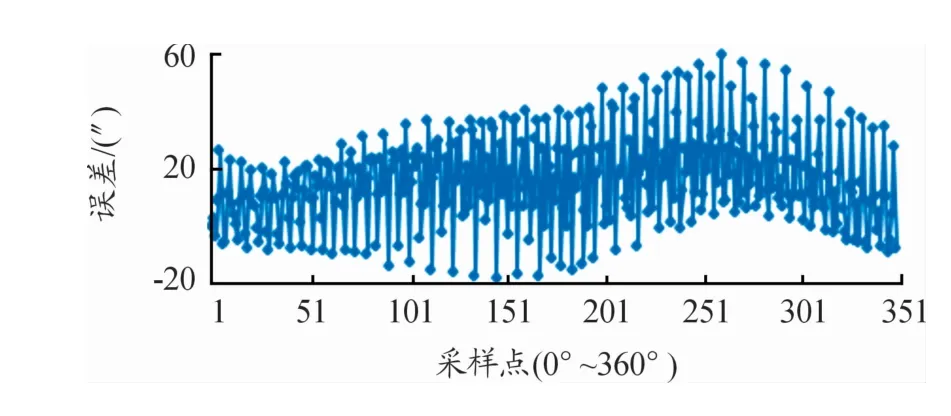
图12 内外通道的整周误差之差曲线（抑制1次误差后）

外环通道的短周期2次误差，主要原因为传感器的电气系统容易存在“两路信号幅值不相等”的情况，因为角度解算是由幅值转化为角度的过程。为了减小该2次误差，对SIN信号和COS信号的幅值在角度解算之前进行了补偿。具体的实现方法为：使样机转动大于1个且小于1.5个短周期，获取并记忆两路信号在模数转换后的幅值，并计算出较大幅值与较小幅值的比值作为2次误差补偿系数；在样机正常工作时，将幅值较小的一路信号在计算时乘以补偿系数。

采取了上述抑制短周期2次误差的方法后，64周期外环的短周期误差峰－峰值减小了约24%，最终的短周期和整周测量误差曲线分别如图13和14所示，短周期误差为－8.8″～14.7″（峰－峰值23.5″），整周误差为－11.7″～20.6″（峰－峰值32.3″）。

图13 64周期外环通道的短周期误差曲线（抑制2次误差后）

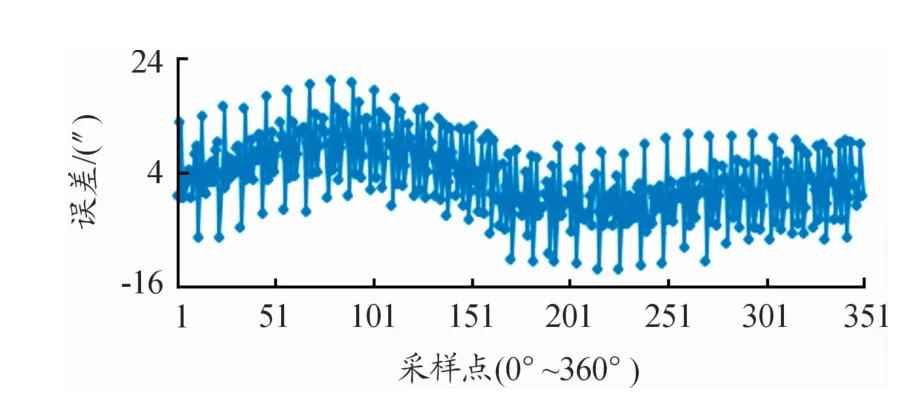
图14 64周期外环通道的整周误差曲线（抑制2次误差后）

5 结论

当传感器的制造、安装、引线、信号处理等环节不理想时，会导致短周期1次和2次误差。在样机的实验中，测试结果表明：传感器的确存在明显的短周期1次和2次误差。根据误差产生的机理，在信号处理环节对短周期1次和2次误差进行了抑制。样机采用了短周期1次抑制方法后，短周期误差峰－峰值减小约1／2；采用了短周期2次抑制方法后，短周期误差峰－峰值进一步减小约1／4。最终，传感器样机的原始短周期误差为－8.8″～14.7″，整周误差为－11.7″～20.6″。虽然抑制效果比较显著，但从样机最终的短周期误差曲线规律中仍可以看出其包含1次和2次成分，且其他高次误差成分也有凸显，说明该传感器在信号处理环节或结构上仍存在提升的空间。