湿式离合器对偶钢片力学响应特性分析

张志刚，张子阳，梁美林，陈永龙，李佳雪，罗 轩

（1.重庆理工大学 汽车零部件先进制造技术教育部重点实验室，重庆 400054； 2.宁波圣龙（集团）有限公司，浙江 宁波 315104）

湿式离合器作为汽车传动系统的核心部件之一，在起步与换挡过程中，摩擦副滑摩产生大量热，大部分热量被对偶钢片吸收，导致对偶钢片盘面温度梯度和应力梯度过大，接触压力分布不均，频繁接合下容易出现局部热点、表面烧蚀、翘曲变形等典型热失效现象，降低湿式离合器的使用性能和可靠性［1］。对偶钢片温度场分布和应力场分布是影响对偶钢片热失效的直接因素，因此研究对偶钢片接触压力、应力应变等力学响应特性的分布规律，进而为湿式离合器对偶钢片热失效分析奠定基础。

Afferrante L等［2］基于湿式离合器摩擦副接触数学模型分析了其接触面温度场和应力场分布规律；Zhao S等［3］采用瞬态温度—位移耦合分析方法，基于二维轴对称模型研究了多片离合器模拟运行工况下的温度场以及接触压力分布，并分析了离合器片厚度和材料属性对其热力学行为的影响；Abdullah O［4］采用ANSYS软件建立多片离合器二维轴对称热结构耦合有限元模型，仿真得到接合初期多片离合器的温度场和接触压力分布；Zagrodzki P［5］基于热弹性接触机理建立热结构耦合有限元模型，并结合实验研究了湿式多片离合器接合过程中热点的产生以及分布规律；张金乐等［6］通过建立湿式换挡离合器热机耦合三维有限元模型，分析了相对转速差、对偶钢片厚度和工作油压对对偶钢片温度场和应力场的影响；王宏伟等［7］建立湿式换挡离合器总成的三维有限元模型，研究了对偶钢片为碟形的摩擦副温度场及应力场分布规律；杨亚联等［8］采用热机耦合仿真方法建立湿式离合器三维有限元模型，研究了摩擦副内外半径差、接合时间和接合次数等因素对钢片的温度场和应力场的影响；陈瑶等［9］采用热结构直接耦合方法对湿式离合器应力场进行计算，研究了工程上湿式离合器活塞不同加压方式对摩擦副应力场的影响规律。综上所述，学者们常采用热机耦合仿真分析方法，未充分考虑摩擦片油槽内润滑油与对偶钢片摩擦表面之间的热交换，降低了分析结果的准确性。

本文针对现有研究的不足，以热结构直接耦合法为基础，考虑摩擦片油槽内润滑油与摩擦副的对流换热，建立湿式离合器摩擦副三维热流固强耦合有限元模型，研究了湿式离合器接合过程中对偶钢片力学响应特性变化规律，为湿式离合器热失效分析提供理论支持。

1 湿式离合器热流固耦合分析理论

1.1 摩擦副生热模型

湿式离合器摩擦副接合过程中，摩擦副间隙中的润滑油被挤出，摩擦表面处于边界摩擦状态，相互滑摩产生大量热，不考虑材料磨损的影响，所有的滑摩功都转化为摩擦热并全部由摩擦副吸收［10－11］。用热流密度表示单位时间单位面积摩擦表面滑摩产生的热量，热流密度计算模型如下所示。

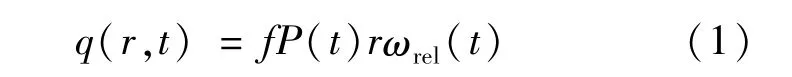
式中：r为湿式离合器摩擦表面任意位置处半径（m）；f为滑动摩擦因数，f＝0.13－0.008log（ωrel）；P（t）为摩擦副控制油压（Pa）；ωrel（t）为摩擦副相对角速度（rad／s）；t为接合时间（s）；q（r，t）为湿式离合器摩擦副热流密度（W／m2）。

由于摩擦副材料物理性能参数的差异，对偶钢片和摩擦片各自吸收的热量不同，为进一步分析摩擦副热量分配情况，基于摩擦副材料物理参数，引入摩擦副热流分配系数如下：

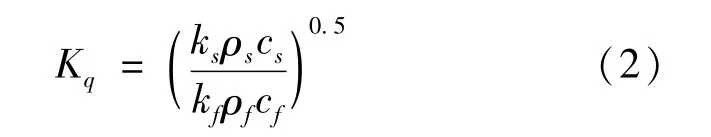
用热流密度表示摩擦副产生的热量，对偶钢片和摩擦片的摩擦表面热流密度分别为

式中：Kq为热流分配系数；ρ、c、k分别表示密度、比热容和导热系数；s、f为下标，分别表示对偶钢片与摩擦片。

1.2 热流固耦合模型

本文采用STAR－CCM＋与Abaqus协同仿真，通过固体与流体交界面上的数据交换实现两个软件之间的耦合，STAR－CCM＋将热通量数据传递给Abaqus，Abaqus将温度信息反馈给STAR－CCM＋，两个软件同时运行，并在每个时间步结束时自动交换数据，属于两个代码之间的强耦合。

在耦合模型中，润滑油迅速流经油槽，润滑时间短，温度变化小，忽略润滑油特性参数随温度的变化，且摩擦副变形小，基本不影响流体流动，因此，忽略变形场对流场的影响以及流场压力对固体变形的影响，分别建立耦合变形场方程和耦合温度场方程。

1）固体耦合变形场方程

假设摩擦副始终处于弹性变形阶段，考虑温度场变化，摩擦副接合过程中产生的变形由外力作用产生的弹性变形和温度变化引起的热变形叠加而成［12］，温度变化不影响切应变，因此摩擦副应变方程为

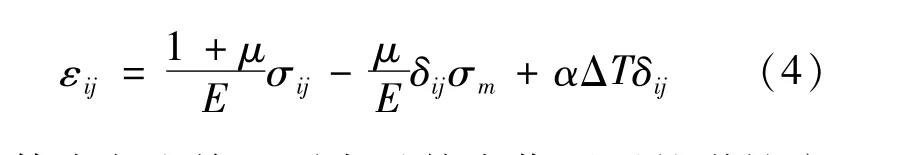
式中：等式右边前两项表示外力作用下的弹性应变，第3项表示热应变。εij表示应变，下标i、j分别取值1、2、3，i＝j为正应变，i≠j为切应变；μ为泊松比；E为弹性模量；σij、σm为应力，其中σm＝σx＋σy＋σz，σx、σy、σz分别表示沿坐标轴方向的正应力；α表示热膨胀系数；ΔT为温度变化量；其中，i＝j时δij＝1，i≠j时δij＝0。

摩擦副在外力作用下处于平衡状态，在内部任取一点M都处于平衡状态，通过对点M领域内的六面体微元受力平衡分析得到其静力平衡方程为

式中：Fx、Fy、Fz为外力沿x、y、z方向的分量（N）；σx、σy、σz为各微元面上沿x、y、z方向的正应力（Pa）；τxy、τyx、τxz、τzx、τyz、τzy为各微元面上的切应力（Pa）。

结合式（4）（5），推导得到摩擦副耦合变形方程为

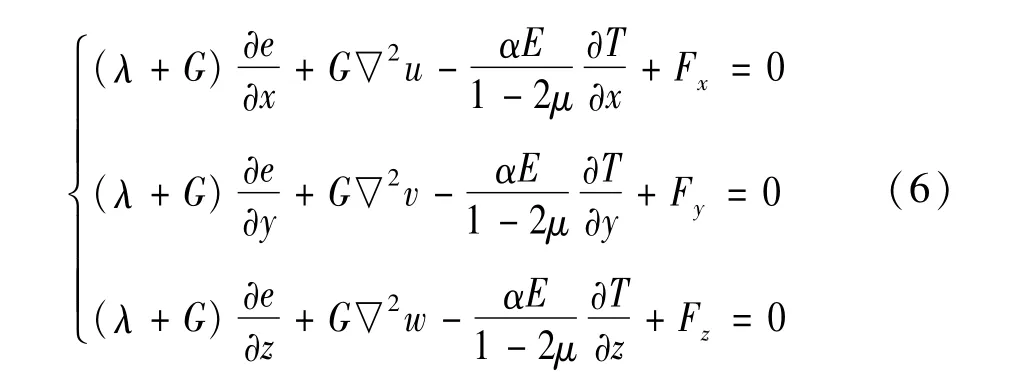
式中：λ、G均表示拉梅常数，也称剪切模量λ＝；u、v、w分别表示沿x、y、z坐标轴的位移分量；Fx、Fy、Fz分别表示外力沿坐标轴方向的分量；e为体积应变，e＝εx＋εy＋εz；▽2为拉普拉斯算子，▽2＝∂／∂x2＋∂／∂y2＋∂／∂z2；该变形方程中有温度场变化的耦合项，体现了温度场对固体变形场的影响。

2）耦合温度场方程

不考虑材料磨损的影响，根据能量守恒，认为所有滑摩功都转换成摩擦热并被摩擦副和润滑油吸收。摩擦副通过热传导吸收热量，单位时间单位体积热传导吸收热量［12］为

摩擦副变形影响温度场分布，单位时间单位体积变形吸收的热量为

综合式（7）（8），得到摩擦副热平衡方程为

润滑油与摩擦副进行对流换热，并通过热对流和热传导吸收热量［12］，单位时间单位体积润滑油热对流吸收的热量为

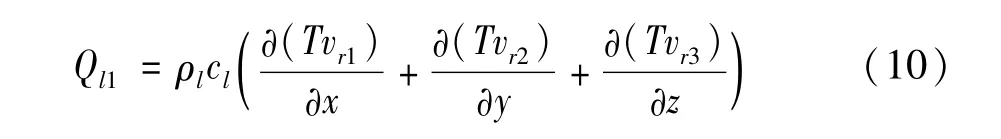
单位时间单位体积润滑油热传导吸收的热量为

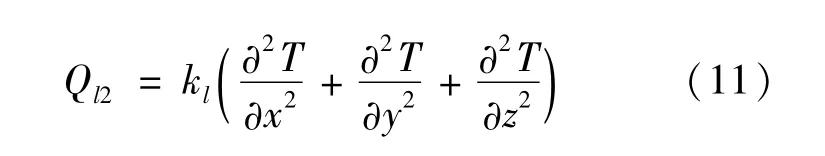
综合式（10）（11），得到润滑油热平衡方程为

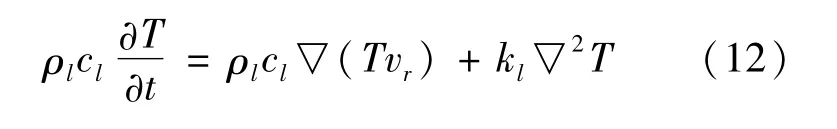
因此，考虑变形场和流场对温度场的影响，综合式（9）（12），得到的耦合温度场方程为

式中：l代表润滑油，i＝1，2，3分别代表对偶钢片、摩擦衬片和摩擦基片；vr1、vr2、vr3分别表示润滑油相对摩擦副的流速沿坐标轴方向的分量。

2 湿式离合器热流固耦合有限元模型

2.1 建立固体有限元模型

2.1.1 固体三维模型

湿式离合器由多片环状对偶钢片和摩擦片相间布置而成，根据湿式离合器实际结构参数，运用CATIA软件建立湿式离合器三维模型，如图1所示。该模型主要由4片对偶钢片和3片摩擦片相间布置而成，摩擦片由摩擦基片和摩擦衬片构成，其上分布有多个油槽，便于对摩擦副冷却散热。摩擦片和对偶钢片通过花键分别与内、外毂相连接，活塞加压使摩擦副接合，卡环与外毂连接，固定不动限制摩擦副的移动。为了便于分析和对比，分别将对偶钢片从左到右编为对偶钢片＃1、对偶钢片＃2、对偶钢片＃3和对偶钢片＃4；摩擦片从左到右编为摩擦片＃1、摩擦片＃2和摩擦片＃3。将所建固体三维模型导入Abaqus软件进行网格划分，如图2所示。

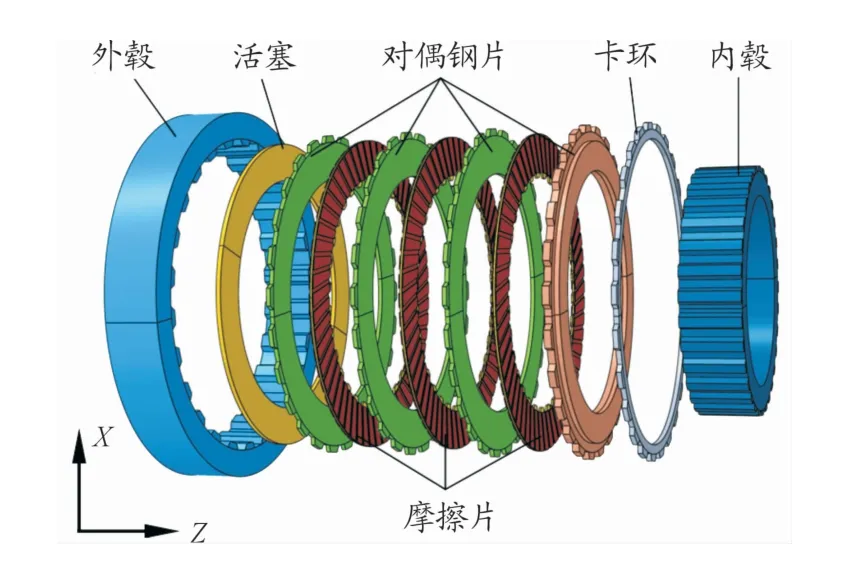
图1 湿式离合器三维模型

图2 湿式离合器固体有限元网格模型

2.1.2 材料特性

对偶钢片和摩擦基片材料相同，摩擦衬片为纸基材料，假设材料为各向同性，工作过程中物理特性参数保持不变［13］，材料参数如表1所示。

表1 摩擦副材料参数

2.1.3 边界条件

1）瞬态热边界条件

湿式离合器接合过程中，对偶钢片与摩擦片存在转速差，在接合油压的作用下，摩擦产生大量热并被摩擦副和润滑油吸收。湿式离合器摩擦副与润滑油之间的对流换热属于一种无相变的强制对流换热，包括摩擦片油槽、摩擦副接合表面及摩擦副内外环面与润滑油之间的对流换热3部分。其中，油槽内润滑油与摩擦副之间的对流换热通过建立热流固耦合仿真模型实现，摩擦副接合表面、内外环面与润滑油之间的对流换热通过实验关联式计算其对流换热系数，并将该对流换热系数添加到固体有限元模型中实现。根据汽车正常工作下变速器实际情况，设定模型初始温度为70℃［6］。

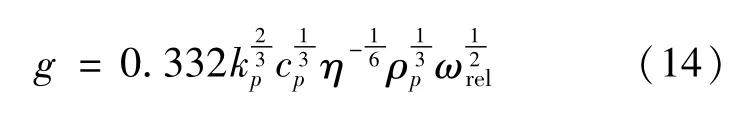
式中：kp为润滑油导热系数（W／（m·k））；cp为润滑油比热容（J／（kg·K））；η为润滑油动力黏度（Pa·s）；ρp为润滑油密度（kg／m3）；p为下标，表示润滑油。

摩擦副内外环面与润滑油之间的换热等效为流体横掠单管对流换热［15］

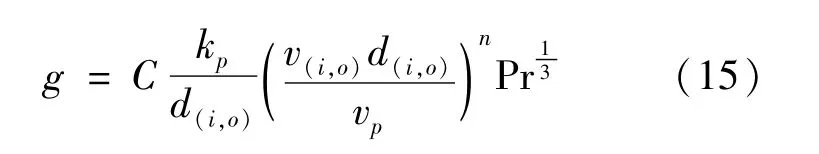
式中：Pr为普朗克常数；C、n为常数，根据雷诺数确定；v为内外环面线速度（m／s）；d为摩擦副直径（m）；i、o为下标，分别表示摩擦副内、外径；vp为润滑油运动黏度（m2／s）。

2）位移边界条件

在湿式离合器有限元仿真建模过程中，将摩擦副的滑摩过程等效为对偶钢片静止不转，摩擦片从初始转速匀减速为零［6］，摩擦片的初始转速即为摩擦副最大相对滑摩转速。根据湿式离合器实际运动关系，在离合器内毂中心设置参考点，控制摩擦片转动，给定摩擦片初始转速为1 500 r／min；对偶钢片静止不动，固定离合器外毂，通过外毂约束对偶钢片运动；选取活塞表面施加均匀压力，活塞只存在轴向运动，约束其余各方向自由度；卡环固定限制摩擦副移动。滑摩时间为0.5 s，接合过程活塞表 面压力P的变化通过拟合试验数据得到

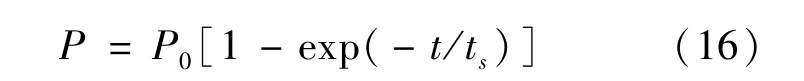
式中：t为滑摩时间；P0为设定达到的接合压力；ts为压力迟滞时间。

2.2 建立流体有限元模型

2.2.1 流体三维模型

湿式离合器工作在封闭浸油的环境中，在工作过程中，润滑油沿径向由内向外循环通过油槽，实现对摩擦副的冷却作用，流体三维模型如图3所示。

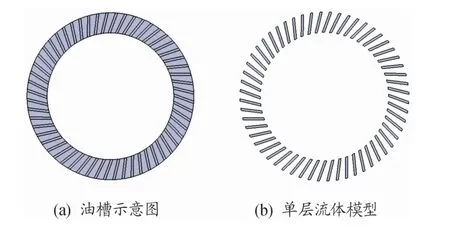
图3 流体三维模型示意图

图3（a）为摩擦片油槽示意图，对该模型在CATIA软件中进行布尔减操作，得到图3（b）所示的湿式离合器油槽内流体三维模型。通过划分网格、选择物理模型、定义边界条件等建立流体域有限元模型。

④IT服务外包作为一种市场化活动，市场规律自然蕴涵其中，管理意识的弱化是服务方减少供给、压缩成本、风险放大的直接诱因，放任式的服务外包会引发因服务外包而带来的新风险。

图4所示为单个油槽内流体网格模型，润滑油由内向外流经油槽，分别定义流体内径速度进口、外径压力出口和周向壁面边界类型，选择表面重构、多面体单元划分流体网格。

图4 流体域网格模型

湿式离合器接合过程中，润滑油速度随时间变化，其特性参数如表2所示，属于不可压非定常层流流动牛顿流体，流体物理模型选择隐式不定常时间格式、分离流体、恒密度状态方程等。

表2 润滑油参数

2.2.2 边界条件

流体边界条件包括进口、出口及壁面边界条件。根据湿式离合器润滑油流量确定入口流速，设置速度进口边界条件，湿式离合器工作过程中不断进行冷循环，假设进油口温度恒定并保持在70℃［16］。设置压力出口边界条件，定义一个大气压。流体与固体通过耦合面交换热量，分别确定流体－摩擦片耦合面和流体－对偶钢片耦合面，设置耦合面热规范条件为温度，指定耦合面与外部程序耦合。流体与摩擦片同步旋转，定义场函数，添加旋转运动，使流体与摩擦片以相同的转速运动。

3 仿真结果分析

应用Abaqus与STAR－CCM＋协同仿真建立湿式离合器热流固耦合模型，针对湿式离合器起步接合工况，对摩擦副温度场、变形场和流场进行耦合计算，得到对偶钢片在接合过程中的接触压力特性、应力应变特性的分布规律。

3.1 接触压力特性分析

图5为湿式离合器对偶钢片接触表面局部示意图，沿径向选取3个结点，分别代表对偶钢片内径、中径和外径，研究其接触压力分布规律。

图5 对偶钢片接触表面局部示意图

图6（a）为湿式离合器接合过程中控制油压与对偶钢片接触表面各结点接触压力随时间变化曲线。从图中可以看出：在摩擦副接合过程中，各结点接触压力变化趋势与控制油压变化趋势一致，但结点2接触压力显著高于控制油压和结点1、3的接触压力。结点1、3在滑摩中后期接触压力较低，且低于控制油压，说明对偶钢片接合过程中盘面接触压力沿径向分布不均匀，中径接触压力较高，内、外径接触压力较低，摩擦副接合过程中较容易发生不均匀变形。图6（b）为接合完成时各对偶钢片盘面接触压力沿径向的变化曲线。从图中可以看出：各对偶钢片接触压力沿径向分布不均匀，高压力区集中在盘面中间区域。对于多对摩擦副，随着对偶钢片逐渐远离活塞端，对偶钢片盘面高压区逐渐向外径移动。

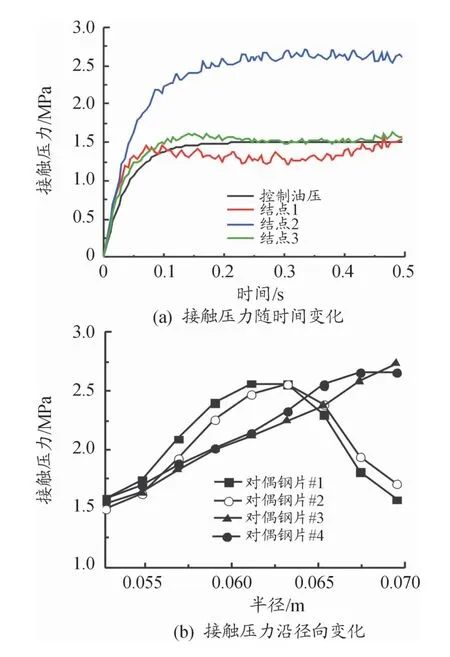
图6 对偶钢片接触面接触压力变化

为进一步分析对偶钢片接触压力特性，得到各对偶钢片最大接触压力和对偶钢片名义平均接触压力随时间变化曲线如图7（a）所示。从图中可以看出：在摩擦副接合过程中，对偶钢片最大接触压力与名义平均接触压力随时间变化趋势一致，但各对偶钢片最大接触压力显著大于钢片的名义平均接触压力。为进一步分析摩擦副接触压力分布不均匀性，引入接触压力扰动系数K，得到各对偶钢片接触压力扰动系数随时间变化曲线如图7（b）所示。接触压力扰动系数K表明了对偶钢片最大接触压力与名义平均接触压力的比值，K值越大，摩擦副接触面接触压力扰动越大，接触特性越差，对偶钢片越有可能出现局部高温与高应力区，进而导致湿式离合器失效［17］，从图7中可看出对偶钢片＃3的承受负荷较大。

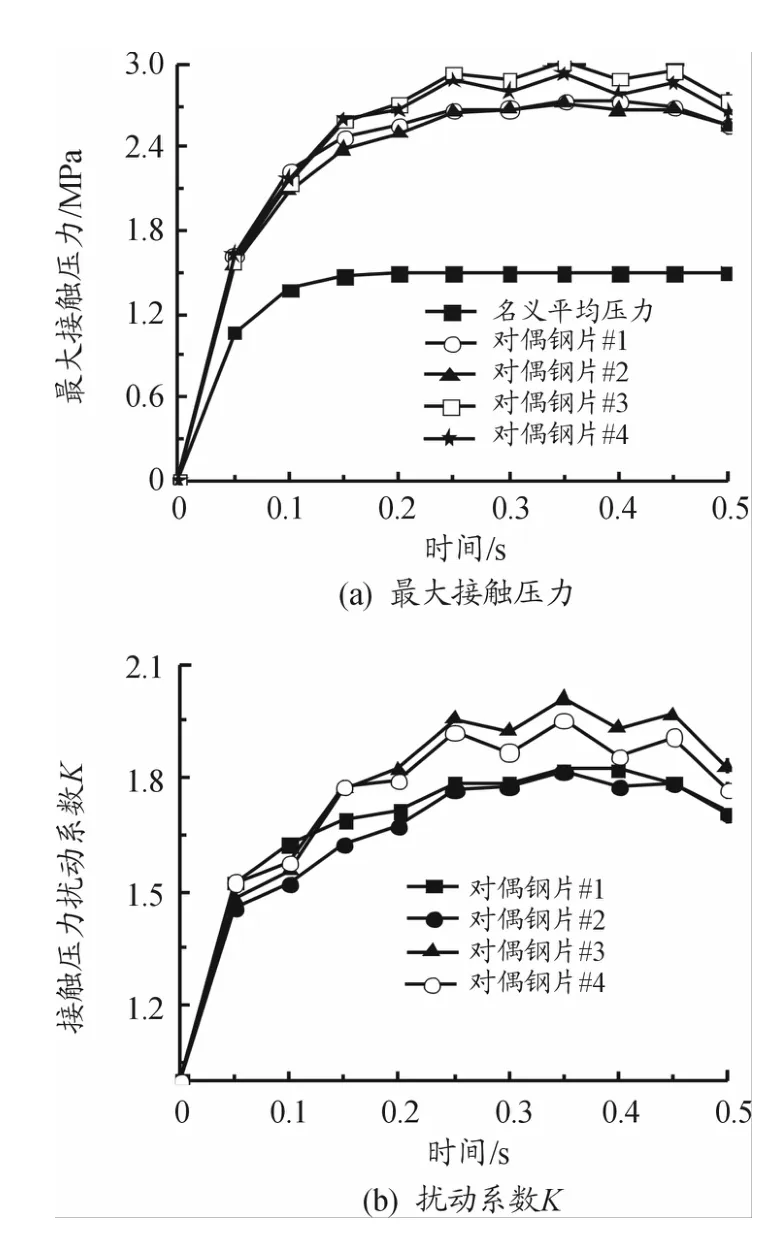
图7 对偶钢片接触压力扰动

3.2 应力应变特性分析

1）应力特性分析

图8（a）为对偶钢片接触面各应力沿径向的变化曲线。从图中可以看出：周向应力远远大于其余各方向应力，认为周向应力是导致对偶钢片失效的主要应力［13］。得到各对偶钢片最大周向应力随时间变化曲线如图8（b）所示，从图中可以看出：摩擦副接合过程中，对偶钢片最大周向应力随时间逐渐增大，在接合后期略有减小。其中，对偶钢片＃2、＃3的周向应力明显大于对偶钢片＃1、＃4，这是因为对偶钢片＃2、＃3位于摩擦副中间位置，两端面均与摩擦片接触，接合过程中承受的负荷较大，温度较高，热应力较大，在湿式离合器接合过程中更容易因热应力过大而出现热失效。下面以对偶钢片＃3为例分析对偶钢片盘面周向应力分布规律。

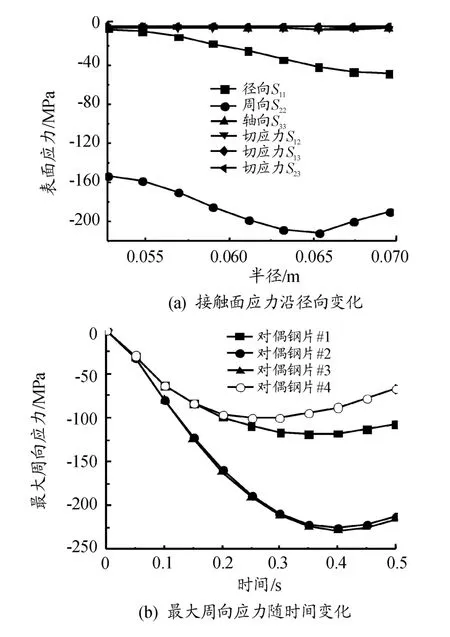
图8 对偶钢片接触面应力分布

图9（a）为摩擦副接合完成时刻对偶钢片接触表面周向应力分布云图。从图中可以看出：对偶钢片周向应力沿圆周方向分布均匀，且该周向应力为负，表现为压缩应力，这是由于对偶钢片在热载荷和外部约束下无法自由膨胀变形引起的［18］。图9（b）为对偶钢片接合过程中不同时刻周向应力沿径向的变化曲线。从图中可以看出：周向应力随时间先增大后减小，径向分布不均匀，沿径向先增大后减小，高应力区集中分布在盘面中间区域，这与对偶钢片接触压力分布规律相似。

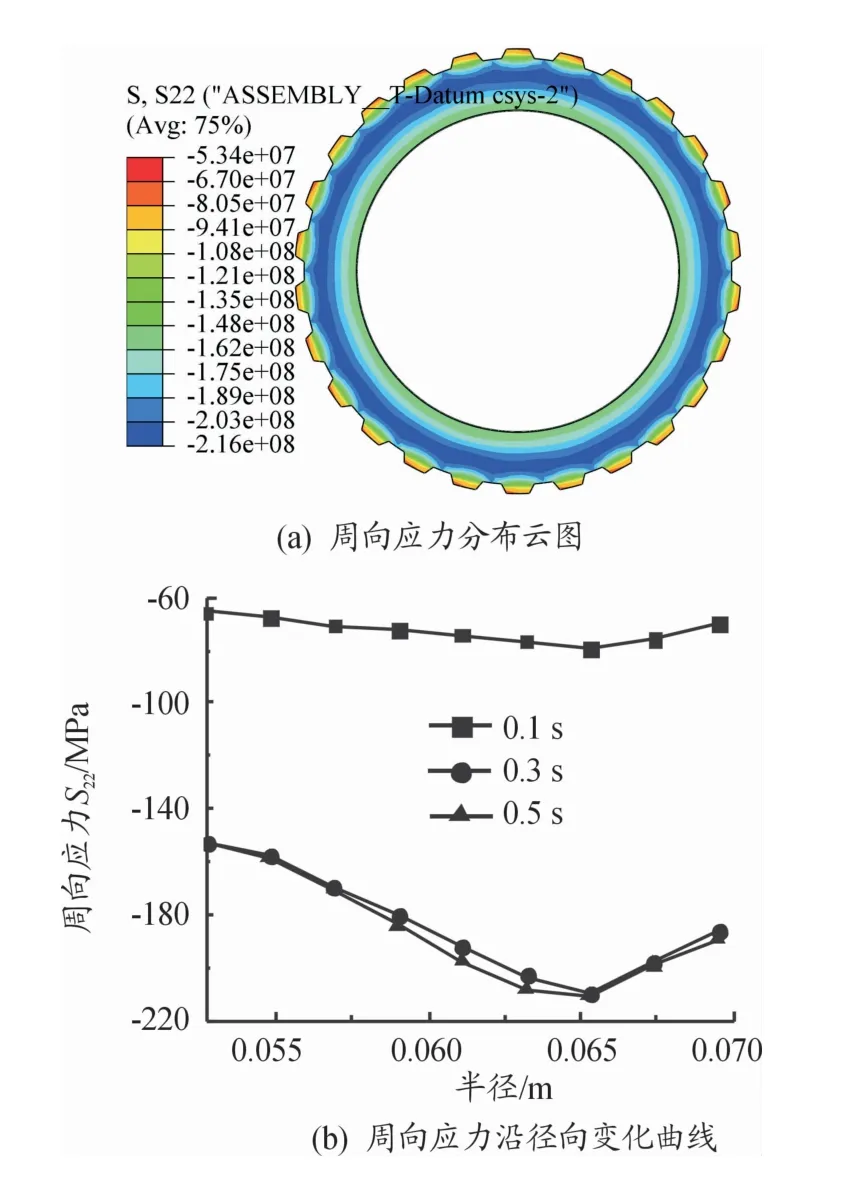
图9 对偶钢片接触面周向应力分布

2）应变特性分析

图10为对偶钢片接触面上各方向总应变沿径向的变化曲线。从图中可以看出：对偶钢片接触面正应变显著大于剪应变。这是因为湿式离合器材料为各向同性，温度变化仅影响材料的正应变，不影响其剪应变，故在考虑对偶钢片变形时忽略其剪应变的影响，主要分析对偶钢片正应变的分布规律。

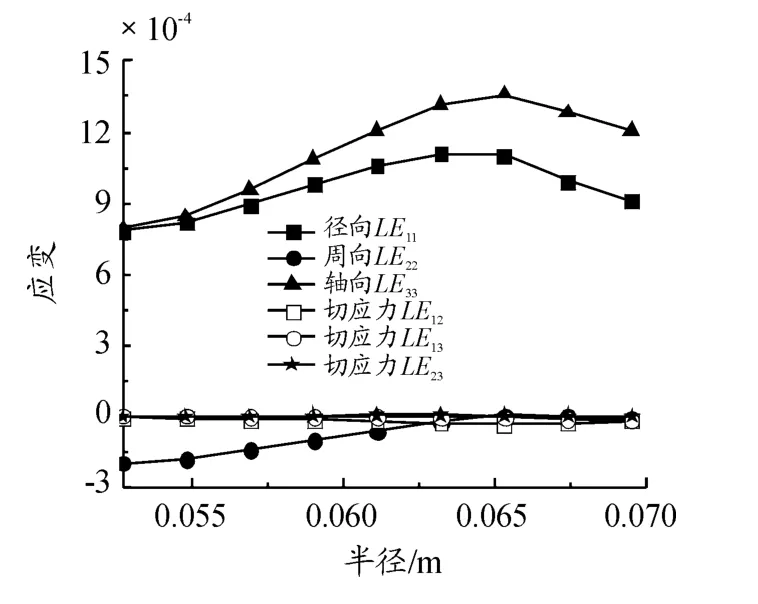
图10 对偶钢片总应变沿径向变化

图11分别为对偶钢片接触面径向、周向以及轴向正应变沿径向的变化曲线。从图中可以看出：对偶钢片材料各向同性，沿各个方向的热应变相同。对偶钢片总应变由弹性应变和热应变共同组成，且热应变略大于弹性应变，认为对偶钢片的变形主要来自于材料热变形，在考虑摩擦副变形时，不能忽略温度的影响。

图11 对偶钢片正应变沿径向变化

图12为各对偶钢片热应变沿径向的变化曲线。从图中可以看出：对偶钢片＃2、＃3的热应变明显大于对偶钢片＃1、＃3。这是因为位于中间位置的对偶钢片＃2、＃3热负荷较大，温度和应力较高，材料受热变形较大。因此在摩擦副的工作过程中，中间位置的对偶钢片发生翘曲变形的可能性较大。

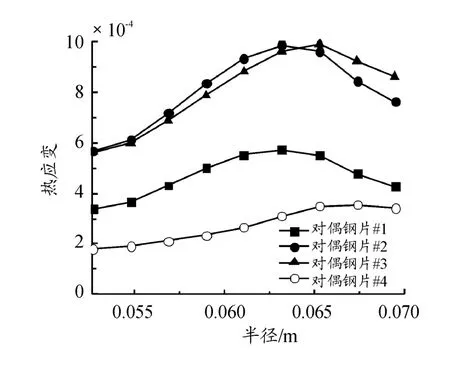
图12 对偶钢片热应变沿径向变化

4 结论

1）对偶钢片接触压力与摩擦副控制油压随时间变化规律一致，接触压力沿径向分布不均匀，高压力区集中盘面中间区域；引入接触压力扰动系数，确定位于摩擦副中间位置的对偶钢片接触特性较差、接触压力扰动较大。

2）对偶钢片周向应力远大于其余各方向应力，是导致对偶钢片失效的主要应力；周向应力沿周向分布均匀，沿径向先增大减小，随时间逐渐增大，位于摩擦副中间位置的对偶钢片周向应力较大，较容易出现热失效。

3）对偶钢片正应变远大于剪应变，材料应变由热应变和弹性应变共同构成，且热应变大于弹性应变，温度变化对对偶钢片变形的影响很大。