基于磁流变液的行星探测器传动装置速度控制策略

李 强，华德正，刘晓帆，刘新华，3

（1.中国矿业大学 机电工程学院，江苏 徐州 221116；2.中国煤炭教育协会，北京 100713；3.姜堰经济开发区科创中心，江苏 泰州 225500）

随着空间技术的飞速发展，行星探测器在未来太空资源开发与利用中的作用将越来越重要［1－3］。在变重力环境下，从电机到负载的传动过程中，不可避免地受到柔性关节的影响。柔性关节给控制系统带来迟滞、非线性耦合、高频共振等问题，对传动系统的精度、平稳性等动态特性有很大影响［4－5］。此外，行星表面的路况复杂，传统的啮合传动元件会因攀爬和障碍物增多而严重磨损。因此，如何保证传动系统的高精度速度控制，延长其使用寿命，对行星车乃至空间机器人的研究具有重要意义。

目前，随着计算机技术的进步，通过改进行星探测车的传动系统结构、建立系统数学模型和优化控制策略等措施，减轻了变重力环境带来的一些不利影响［6－9］。由于探测器传动系统的某些部件具有柔性关节，其动力学模型对每个自由度没有独立的控制输入，因此大多数刚性关节装置的指令算法不能推广到柔性系统［10］。HAO等［11］通过对机械臂关节运动谱的排列，求解了钻机端部轨迹。庞哲楠等［12］提出了一种变重力环境下双臂机器人关节空间轨迹跟踪的自适应模糊控制方法。利用模糊系统的普遍逼近特性，在线逼近系统的重力项，调整未知系统参数的影响，实现稳定控制。然而，整个控制系统跟踪期望轨迹的时间较长，实时性较差。针对空间机器人的传动系统，DU等［13］利用模糊神经网络重构执行器故障。张文辉［14］设计了一种神经网络自适应轨迹控制策略，空间运动的不确定性部分可以自动补偿。根据Lyapunov理论，设计鲁棒控制器来调整神经网络自适应补偿的建模误差，保证系统一致有界性。仿真结果表明：该方法可以提高误差收敛速度，获得较好的控制精度，但该过程需要分配初始调整时间，且计算量大。李富娟［15］采用拉格朗日方法对Stewart并联机器人在变重力环境下的动力学进行分析，并进行了逆动力学仿真。采用蚁群算法和笛卡尔坐标法对全空间Stewart并联机器人进行路径规划，并对其进行姿态和运动控制。但系统控制对复杂环境的适应能力较弱，需要人工调节，运动控制效率低。

在微重力模拟方面，自由落体运动法和抛物线飞行失重法所产生的变重力环境相对较短，远没有达到研究对象运动性能测试所需的时间［16－19］。应用补偿力如水浮、气浮、钢丝绳悬吊法［20－21］等需要对研究对象和实验仪器进行特殊设计，维护成本较高［22－23］，系统稳定性较差［24］。同时，传统啮合传动系统单一优化算法的实时控制能力仍然比较低，啮合连接方式也存在磨损严重、使用寿命短等问题。

本文介绍了一种磁流变液传动装置（MFTD）作为传统啮合传动方式的替代机构。磁流变液是新型智能材料的一个重要分支，其流变特性会在磁场的作用下发生明显的变化［25］。磁流变液在外部磁场的作用下，内部的磁性粒子在毫秒内沿磁场方向链化成链状或柱状结构，呈类固态，然后在撤掉磁场的情况下恢复牛顿流体的原始状态。磁流变液流变特性的变化呈现出迅速性、可逆性与可控性，这些特性使得磁流变液在传动领域中得到了长足的发展。磁流变液传动装置主要分为圆盘式和圆筒式［26］，主要通过调节外加磁场的大小来控制扭矩传递。此外，还可以通过改变磁流变液工作面积［27］、工作间隙［28］等方式来调节传动装置的扭矩传递。目前，磁流变液已广泛应用于离合器［29－30］、制动器［31－32］以及阻尼器［33－34］等传动装置。本文提出了一种磁流变液传动装置的自适应模糊PID控制策略。此外，通过与常规PID控制的比较，对二者进行仿真分析并通过搭建实验平台进行仿真验证，结果表明自适应模糊PID控制策略能有效地解决变重力和复杂路面引起的传动系统速度波动问题。

1 磁流变液传动装置（MFTD）及动力传递模型构建

1.1 MFTD结构

将MFTD应用于行星探测器传动系统中，该系统可以在变重力环境下调节柔性关节引起的速度波动，达到输出稳定速度的目的。磁流变液所传递的扭矩由两部分组成：当无磁场作用时，磁流变液本身具有一定的黏度，能够传递的扭矩有限；将电磁线圈通电，磁流变液中具有的磁性粒子会立即沿磁场方向链化成链状或柱状的结构，传递较大的扭矩。MFTD的原理如图1所示。

图1 MFTD示意图

圆盘结构的MFTD具有结构简单、响应迅速、惯性小等优点，可组成多圆盘形式，有效地提高传动扭矩。励磁线圈绕组设置在MFTD外壳内，装置体积小、磁阻低、磁场利用率高。磁感线垂直穿过磁流变液剪切方向时的剪切应力比水平通道内产生的剪切应力大得多。因此，该设计是合理的，可以保证磁感线能最大限度地与磁流变液剪切方向垂直。

1.2 磁流变液的剪切应力计算模型

在理想条件下，磁性粒子在磁场作用下链化并排列形成链状结构，当发生剪切作用时链状结构会被拉长，如图2所示。

图2 磁链结构（a）和剪切发生时磁链 变化示意图（b）

假设磁性粒子为均匀球体，每条单链的磁矩为

式中：ri为粒子半径；μ0为真空磁导率；χ为磁性粒子的磁化率；H为磁场强度。

忽略磁极化强度的条件下，磁感应强度B可表示为

此时可以得到磁性颗粒的磁极强度为

当只考虑磁相互作用时，2个粒子之间的静磁力可以通过库仑定律求得

式中，kk为库仑常数；d为2个颗粒之间的距离；δ为2个颗粒之间的间隙。

由于重力的影响，磁链可以近似地看作是一条悬链线，如图3所示。

图3 悬链线形式磁链结构（a）和剪切发生时磁链变化示意图（b）

假设磁链的初始悬挂点等高，则悬链线长度可表示为

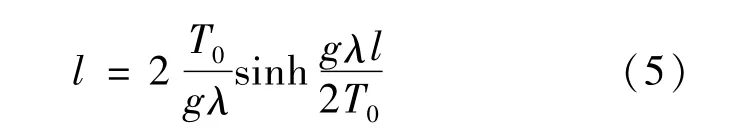
式中：L为板间距离；g为重力加速度；λ为磁链线密度；T0为水平张力，约等于静磁力。

得到单位面积内磁链数为

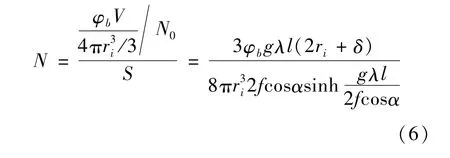
式中：V为磁流变液体积；φb为磁流变液体积分数；S为平板面积；N0为单条链上磁性粒子数。

当剪切作用发生时，磁链在剪切的作用下被拉长，并与磁场方向形成一个切角θ，如图4所示。

图4 磁链剪切变形图

此时，颗粒间距变为d′＝d／cosθ；静磁力为剪切屈服应力为

因此，MRF单位面积剪切屈服应力可以表示为

在变重力环境下，磁流变液单位面积剪切屈服应力为

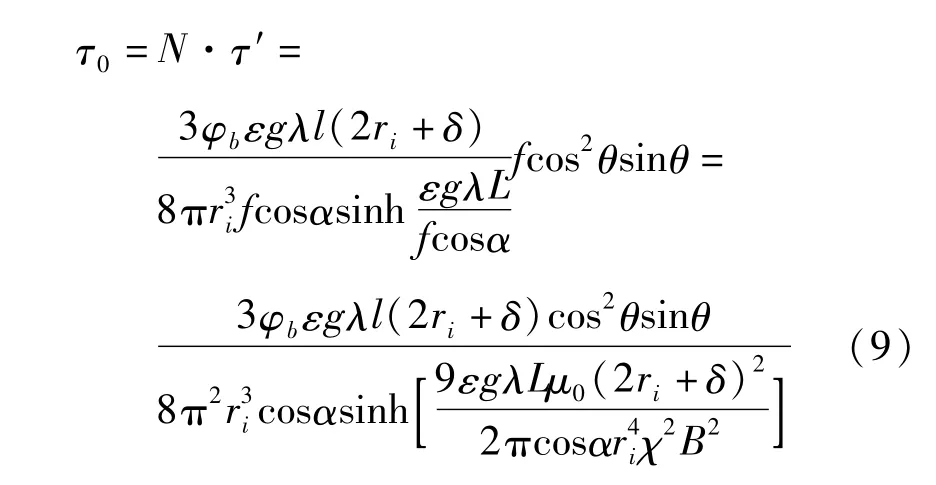
式中，ε为重力系数。

1.3 MFTD中传递扭矩的计算

圆盘MFTD的工作原理如图5所示，其中R1和R2围成的环形区域为MFTD的工作区域。L和H分别为输入盘与输出盘之间的间距和磁场强度。在圆盘半径为r处任取宽度为dr的微环，此微环面上磁流变液所传递的扭矩可以表示为

图5 MFTD工作原理图

式中，τ为磁流变液剪切屈服应力。

设驱动盘和输出盘的转速分别为ω1和ω2，则磁流变液剪切应变率μ为

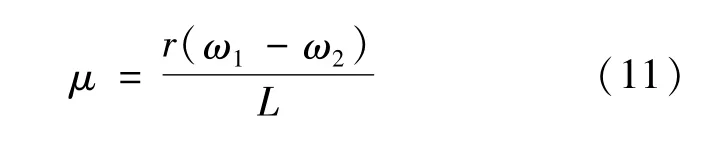
磁流变液的本构关系式为

式中，η为磁流变液的黏度系数。

将式（11）代入式（12）中可以得到磁流变液在磁场作用下的剪切屈服应力为

将式（13）代入式（10）中，得到微环面上磁流变液的微传递扭矩为

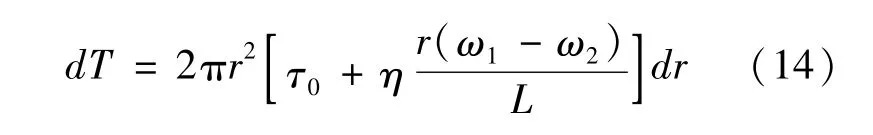
通过积分可以得到圆盘式MFTD工作区内圆盘MFTD传递的扭矩为

从式（15）可以看出，MFTD在工作区内的传递扭矩由两部分组成：①磁流变液的磁性粒子会受到磁场的磁化作用，磁性粒子会沿这磁场方向迅速链化形成链状或柱状结构，增大自身能够传递的扭矩TH数值，不同的磁场强度可以传递不同的扭矩TH数值；②磁流变液基载液本身具有一定的黏性，只能传递有限的扭矩Tη，比TH小得多。

1.4 MFTD控制系统传递函数

为了能够对探测器传动装置的速度进行稳定控制，设计了以磁流变液为工作介质的传动装置。由于磁流变液是由固－液两相材料分散而成，磁性粒子与基载液之间形成的密度差可以改变材料的性能，可能会发生沉降等问题，所以利用理论分析以及精确的数学模型来进行计算具有一定的难度。针对磁流变液的上述特点，本文首先搭建了一个MFTD数据采集实验台。调速系统的机理和实验台布置如图6、7所示。其中MFTD的主要设计参数如表1所示。

图6 MFTD调速系统的机理

表1 MFTD的主要设计参数

由图6可知：I为MFTD线圈励磁电流，T为传递扭矩，Tf为系统的摩擦扭矩，Tl为负载扭矩，ω1和ω2分别是MFTD的输入速度和输出速度，MFTD调速系统的运动方程可表示为

式中：J为MFTD输出端的总惯性矩；dω／dt是系统输出角加速度。将式（16）变形得到

由式（17）可知，当输入速度ω1、摩擦力矩为Tf、负载扭矩为Tl时，MFTD传递的扭矩T可通过I值进行调节，从而改变系统输出端角加速度dω／dt，从而达到控制速度的目的。

从图7可以看出：该实验台主要由三相异步电动机、扭矩速度传感器、DP811A可编程电源、MFTD、磁粉制动器、控制器和示波器等装置组成，可提供0～970 r／min输入转速范围的三相异步电动机，其额定功率是7.5 kW。数显仪表可以将扭矩速度传感器收集到的系统输入端和输出端的扭矩和转速值实时显示。可编程电源可以让MFTD线圈绕组产生可调励磁电流。磁粉制动器可以提供恒扭矩，并通过示波器采集MFTD的响应时间。

图7 MFTD实验平台

利用Matlab系统辨识工具箱对多功能MFTD的数学模型进行辨识和求解。识别数据是在可编程电源调节下的电流值与输出速度，测试数据采用的是另一组数据。MFTD的传递函数为

对MFTD进行系统辨识后，最佳拟合率为94.35%，拟合度较好。式（18）中Kp＝136.73，Tpl＝0.091 379，Tp2＝0.091 928，系统数学模型如下：

2 MFTD速度控制策略

2.1 自适应模糊PID控制器

常规PID控制器原理简单，对模型依赖性小，鲁棒性强。但是，它无法做到依据被控对象的不同要求进行相关参数的在线自整定，对于大非线性且实时变化的系统，控制效果不理想。针对非线性、不确定的复杂系统，模糊控制会产生一定的稳态误差，达到精确的控制效果仍然具有一定难度。自适应模糊PID控制器在实际应用中可以很好地规避常规PID控制以及简单模糊控制具有的不足。图8所示为自适应模糊PID控制系统结构。e和ec分别为输入变量偏差和偏差变化率，用于实时修改PID控制参数KP、KI和KD。其中，自适应模糊PID控制器计算PID参数的方法见式（20）。

图8 自适应模糊PID控制系统结构

其中，MFTD的e（k）和ec（k）是第一次采样时间k的输出速度偏差和偏差变化率；KUP、KUI和KUD是相应的采样时间比例、积分和微分增量系数；KP0、KI0和KD0是传输装置的初始PID参数ΔKP（k），ΔKI（k）和ΔKD（k）分别为KP、KI和KD的修正值。

实验台测得的输出转速偏差范围为［－60，60］r／min，其基本论域为［－60，60］，输出转速偏差变化率［－400，400］r／min，其基本论域为［－400，400］。此外，对于模糊域，将MFTD的速度偏差和偏差变化率的范围定义为［－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6］，其中7个语言值由［NB，NM，NS，ZO，PS，PM，PB］表示，可以表示为负大，负中，负小，零，正小，阳性中、阳性大。偏差e和偏差变化率ec的模糊量化因子分别为Ke和Kec，其表达式如下

根据实验结果，将ΔKP、ΔKI和ΔKD的基本域设为［－6，6］，ΔKP、ΔKI和ΔKD的输出模糊域分别为［－6，－5，－4，－3，－2，－1，0，1，2，3，4，5，6］，其中［NB，NM，NS，ZO，PS，PM，PB］为所取的7个语言值，表示PID控制系统中的负大，负中，负小，零，正小，正中，正大。根据实验数据和PID参数整定规则，可以得出KP、KI和KD为MFTD输出速度的自适应模糊PID控制参数。

2.2 MFTD仿真分析

研究对象的调节效果至关重要的一步就是对常规PID控制的比例、积分以及微分参数进行分析。通过Matlab／Simulink中的信号约束模块，对PID参数进行整定和优化，对得到的参数进行多次实验和调整。最后，确定自适应模糊PID控制器的初始参数KP＝15，KI＝0.7，KD＝0.08，MFTD的自适应模糊PID控制系统模型如图9所示。

图9 MFTD自适应模糊PID控制系统模型

为了分析自适应模糊PID控制器的性能，对MFTD的速度控制系统进行了仿真实验并对实验数据进行了分析，并与常规PID控制器进行比较。两个控制器的阶跃响应曲线如图10所示，将单位阶跃信号输入常规PID和自适应模糊PID两个仿真模型中，理想情况下的响应曲线为曲线1，常规PID控制器的单位阶跃响应曲线为曲线2，自适应模糊PID控制器的单位阶跃响应曲线为曲线3。常规PID控制器的超调量为11.6%，自适应模糊PID控制器的超调量为0。常规PID控制器所需要的上升时间为0.045 0 s，而自适应模糊PID控制器所需要的上升时间减小到0.027 5 s，调整时间也从0.455 2 s减少到0.035 5 s。

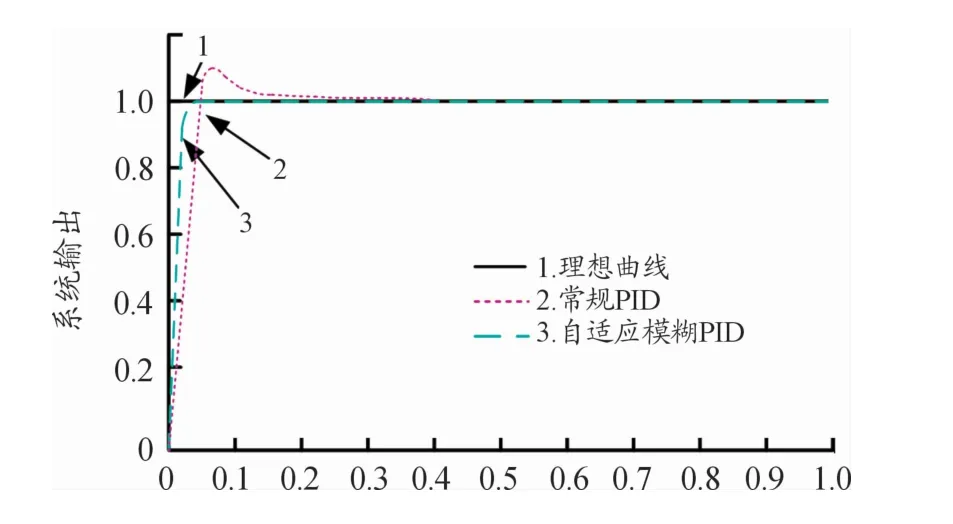
图10 两个控制器的阶跃响应曲线

根据两种控制器速度跟踪性能的仿真实验数据，可以得出2种控制器的速度跟踪性能，两种控制器的速度跟踪曲线如图11、12所示。从图中可以看出：常规PID控制器具有明显的速度跟踪误差，而自适应模糊PID控制器的速度跟踪误差较小，具有良好的速度跟踪性能。

图11 常规PID速度跟踪曲线

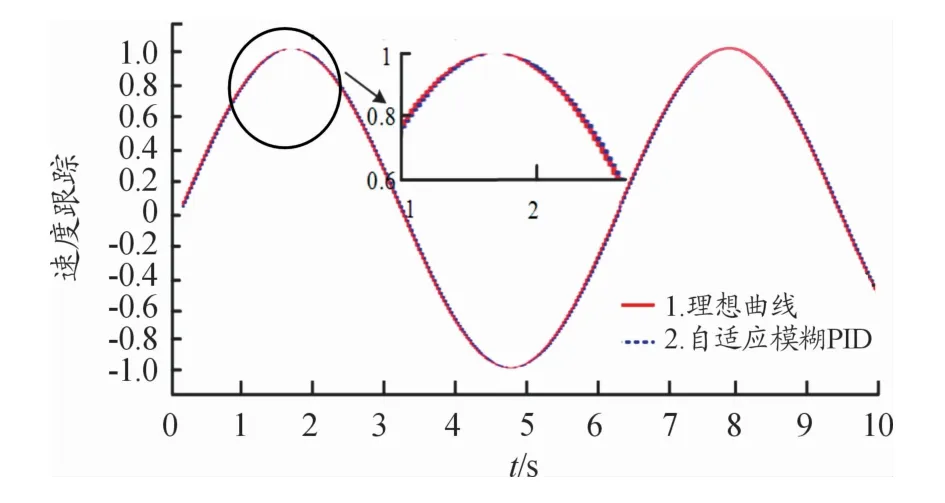
图12 自适应模糊PID速度跟踪曲线

根据以上2种仿真实验结果分析，可以看出自适应模糊PID控制器的响应输出时间减小，可以更快、更稳地达到稳定状态，且无超调。因此，自适应模糊PID控制器的性能更加符合MFTD速度控制系统的要求。

3 实验结果与分析

为了验证MFTD输出速度的稳定性，进行了调速实验，测试了自适应模糊PID控制器保持设定目标转速的能力。首先，将传感器检测到的存储在PCI数据采集卡中的实时速度数据传送到上位机进行进一步处理。然后，控制器、常规PID控制器或自适应模糊PID控制器通过访问处理后的转速值，通过串口通信将信号传送给DP811A可编程电源。最后，通过改变MFTD线圈的电流来改变磁流变液的剪切屈服强度，从而实现速度控制。具体实验设备见图7。

通过调节变频器，将MFTD的输入转速设定为400 r／min，输出转速编程为150 r／min，60 s后输出转速为300 r／min。常规PID控制器和自适应模糊PID控制器的调速曲线如图13、14所示。

图13 常规PID调速曲线

图14 自适应模糊PID调速曲线

静态差速率是调速系统的一个重要评价指标，可以表示为

式中：nmax为最大输出速度；nmin为最小输出速度；Δn为最大输出速度和最小输出速度之间的差值；nm为最大输出速度和最小输出速度的平均值。根据图13、14可知：常规PID控制器和自适应模糊PID控制器在输出速度设置为150 r／min的情况下，静差率达到12.18%和8.76%；在输出速度设置为300 r／min的情况下，其静差率分别达到了5%和3.4%。

速度波动率是速度控制系统的另一个评价指标，可以表示为

式中，n0为设定输出速度的目标值。当输出转速设定为150 r／min时，常规PID控制和自适应模糊PID控制的速度波动率分别为12%和8.7%。当输出转速设定为300 r／min时，其速度波动率分别为5%和3.3%。

4 结论

本文以提高行星探测器传动系统的速度控制精度和减少部件磨损为目标，建立了变重力环境下磁流变液剪切屈服应力计算模型以及磁流变液传动装置（MFTD）模型，阐述了MFTD的结构和原理。此外，通过与常规PID控制器比较，设计了自适应模糊PID控制策略并分别对两种控制器进行仿真和实验。实验显示自适应模糊PID控制可以有效减小传动系统的速度波动，具有较高的运动稳定性。

在未来的研究中，将对MFTD的其他控制策略和优化算法进行研究以获得更好的响应特性并进行变重力环境模拟相关实验测试。