幂级数展开的应用研究

黄 勇 何敏藩

（佛山科学技术学院数学与大数据学院 广东·佛山 528000）

1 研究背景

在本文中，我们主要研究二阶Sturm-Liouville特征值问题，其方程如下：

一般来说，这似乎不太可能以显式的形式获得解析解或是很难获得上述问题的精确值。因此，一些数值方法和近似方法已经实现了确定的Sturm Liouville特征值问题的解决方案。基于渐近校正的Numerov方法和有限元法，Andrew和Paine改进的结果为自然边界条件下的Sturm-Liouville问题。Ghelardnoi采用边界值方法（BVM），对Sturm-Liouville问题进行离散探讨其特征值的近似解，将Andrew-Paine的校正技巧扩展到BVM。在[8]和[9],elik等用Chebyshev配置方法研究高等SturmLiouville方程特征值的近似计算，给出了边界条件的矩阵方程。

在本文中，我们将介绍用于有确定边界条件的Sturm-Liouville问题的特征值的一种简单方法。通过对函数的级数展开，我们将微分方程的未知系数变成一个线性方程组，为使得未知函数有非零解，我们可以由其线性方程组的系数矩阵的行列式为零确定其特征值 。我们将应用该方法计算实例中常用的Sturm-Liouville问题的特征值，并给出其逼近的精度。

2 二阶Sturm-Liouville问题的数值方法

不失一般性，边界条件可以表示如下：

因此，问题就变成求解满足在上述边界条件和二阶常微分方程（1）的未知函数y（x）。

在本部分中，为了避免直接求解微分方程（1），我们介绍一个简单的方法来确定的Sturm-Liouville方程的特征值。首先，我们将y（x）展开成幂级数。如果忽略足够小的误差，那么未知方程y（x）可以近似地展开为：

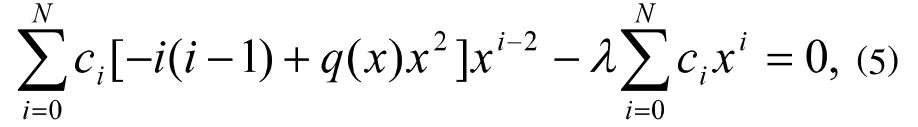
接着我们将方程（5）两侧都乘上（n=0，1，2，…，N-2），然后将新方程关于x在a到b之间求积分，可以得到另外N-1个线性代数方程组的未知系数：

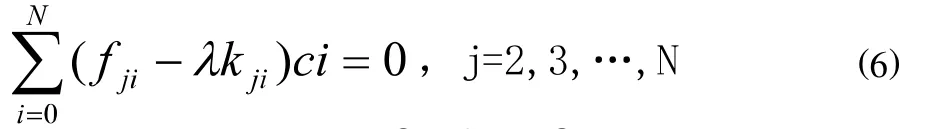
3 Sturm-Liouville问题的数值结果与讨论

为了验证上文所提出的方法的有效性，本节主要讨论常见Sturm-Liouville问题的数值例子，期望得出的精确解和其他数值结果逼近于准确值。我们考虑以下的 Sturm-Liouville问题

例1：特征值的数值结果和绝对误差。

我们考虑以下的Sturm-Liouville问题：

例1：特征值的数值结果和绝对误差

表2：例2特征值的数值结果和绝对误差

4 结论

我们提出一个高效的方法来处理Sturm-Liouville问题。我们不是直接求解微分方程的解，而是利用幂级数将微分方程展开成线性方程组，进一步得到参数的特征方程，通过Matlab编程有效地将特征值计算出来。