一类捕食模型问题解的局部存在唯一性

张璐丹， 张永胜

(洛阳理工学院 数学与物理教学部， 河南 洛阳 471023)

本文针对带有自由边界及变系数和Bedding-DeAngelis响应函数的捕食模型(1)进行研究。

(1)

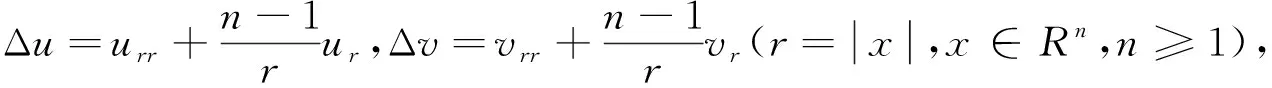
在本文中，假设存在正常数κ1≤κ2使得

0<κ1≤m1(r),m2(r),c(r)≤κ2,kκ1≥λ>0。

(2)

初值函数u0(r),v0(r)满足

u0(h0)=v0(h0)=0,u0,v0>0,r∈[0,h0)。

(3)

1 解的局部存在唯一性

定理1 对任意给定的满足条件(3)的初值函数u0(r),v0(r)以及任意常数γ∈(0,1)，都存在T>0使得问题(1)有唯一解

(u,v,h)∈[C(1+γ)/2,1+γ(DT)]2×C1+γ/2([0,T]);

其中：DT={(t,r)∈R2:t∈[0,T],r∈[0,h(t)]}。T只依赖h0,γ,‖u0‖C2([0,h0])以及‖v0‖C2([0,h0])。

证明：类似于文献[1]，首先引入变量变换将问题(1)化为固定边界条件的初边值问题。令ξ(s)∈C3[0,∞)并且满足

考虑变换

(t,y)→(t,x),x=y+ξ(|y|)(h(t)-h0)y/|y|,y∈Rn。

从而有变换

(t,s)→(t,r),r=s+ξ(s)(h(t)-h0),0≤s<∞。

对于任意t≥0，如果

那么变换x→y是从Rn到Rn上的一个微分同胚映射，从而变换s→r也是一个从[0,∞)到[0,∞)上的一个微分同胚映射。另外，上述变换将自由边界r=h(t)变成固定边界s=h0。

直接计算得

记

u(t,r)=u(t,s+ξ(s)(h(t)-h0)):=U(t,s),

v(t,r)=v(t,s+ξ(s)(h(t)-h0)):=V(t,s),

则自由边界问题(1)化为关于U(t,s)以及V(t,s)的非线性抛物型方程组的初边值问题

(4)

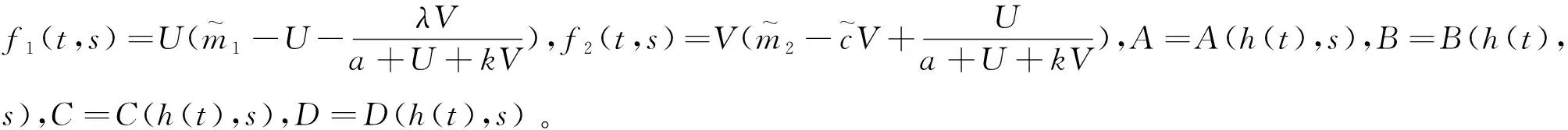
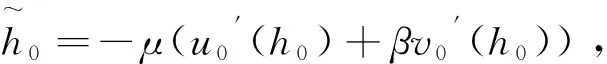
X1T={U∈C([0,T]×[0,h0]):U(0,s)=u0(s),‖U-u0‖C(ΔT)≤1},

X2T={V∈C([0,T]×[0,h0]):V(0,s)=v0(s),‖V-v0‖C(ΔT)≤1},

记XT:=X1T×X2T×X3T，则XT是一个完备的度量空间，其度量为

注意到对于任意h1,h2∈X3T，因为h1(0)=h2(0)=h0，从而有

下面利用压缩映像原理证明问题(1)解的局部存在性和唯一性。对任意(U,V,h)∈XT，考虑线性抛物型方程的初边值问题

(5)

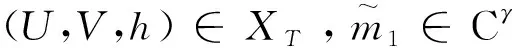
又u0(s)∈C2([0,h0])，由Lp理论以及Sobolev嵌入定理知，问题(5)存在唯一解

(6)

而且

(7)

其中：K1是一个依赖于h0,γ,‖u0‖C2([0,h0])以及‖v0‖C2([0,h0])的正常数。同样地，对任意(U,V,h)∈XT,线性抛物型方程

(8)

存在唯一解

(9)

而且

(10)

其中：K2是一个依赖于h0,γ,‖u0‖C2([0,h0])以及‖v0‖C2([0,h0])的正常数。

定义

(11)

定义如下一个映射F:XT→[C(ΔT)]2×C1([0,T])使得

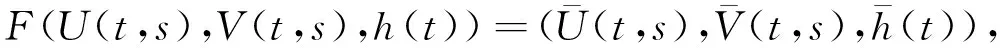
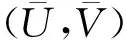
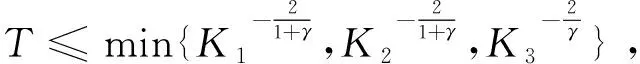
而且

其中：

由LP理论以及Sobolev嵌入定理知

其中：K4仅与h0,‖u0‖C2([0,h0])以及‖v0‖C2([0,h0])有关。同理可得

其中K5，K6仅与h0,‖u0‖C2([0,h0])以及‖v0‖C2([0,h0])有关，又因为

从而当T≤1时有

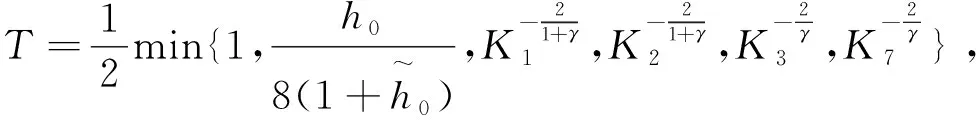
由压缩映像原理知，在XT中存在唯一的不动点(U(t,s),V(t,s),h(t))，即(U(t,s),V(t,s),h(t))是问题(4)的唯一解，从而(u(t,r),v(t,r),h(t))是问题(1)的唯一解。

2 结 语

带有Bedding-DeAngelis响应函数的捕食模型很好地反映了捕食者之间的相互影响。它不仅包含捕食者寻找和处理猎物的时间分配，而且也反映了捕食者之间相互影响的程度。本文利用线性方程理论和压缩映像原理对解的局部存在唯一性进行了精细的分析，这对捕食者与被捕食者的生存与蔓延的研究具有重要的理论意义。