基于矩阵分解的图形渐变避免自交算法研究

吕福起

（重庆财经学院软件学院 重庆 401320）

1 引言

将源图形和目标图形按照某种对应方法[1]并采用合理的插值方法[2]，实现从源图形到目标图形的自然、流畅的过渡为图形渐变技术的核心内容。图形渐变技术在图像融合、计算机动画、矿体形变、计算机视觉等领域都有一定的应用价值，特别是计算机动画技术中实现中间帧能够大幅提高工作效率。图形的对应问题和插值路径问题问图形渐变技术的两大重要问题。关于图形的对应有基于物理模型的对应方法[3]和基于几何图形的对应方法[4]，物理的方法是通过对物体的做功，将伸缩变换、旋转变换和平移变换三个重要指标，应用到顶点对应中去，找到合理的初始图形到目标图形的对应方式。几何的方法是通过建立相似度量函数，通过求解该函数的最有解来寻找最佳对应，该过程可以是动态的。关于插值路径的方法有两大类，一类是通过边角的插值算法[5]，另一类是同构三角网格剖分算法，把图形的插值问题转化成通过三角网格同构剖分后的渐变问题[6]。通过顶点对应方法和边角插值法容易实现，但是对应和插值中难以保证单调一致性的变化，从而出现自交或萎缩现象，见图1和图2。

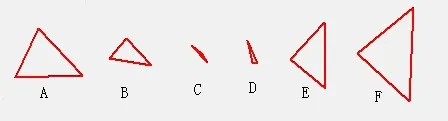
图1 三角形出现萎缩变形序列

图2 直立树到偏向树自交变形序列

2 几何法图形渐变序列算法及存在问题分析

几何法图形渐变序列的形成，主要是基于边角的插值方法，通过插值初始图形和目标图形的边角，通过计算机不断绘制中间图形，从而形成变形序列。但由于方法存在的缺陷，很难在图形的对应中找到最合适的对应，在渐变中出现图形局部扭曲，局部缺失，或局部变动异常，出现图形渐变中的不自然、不光滑现象。

为解决图形渐变序列中的不足，需尽可能使图形简单化，从而更容易处理。为达到此目的，一个常用的方法是将图形进行分解成一个个三角形状态，对三角形顶点进行插值，形成渐变序列。假设初始三角形P和目标三角形Q，三个顶点为，三角形P通过插值算法渐变到Q，中间形成三角形渐变图形序列，为得到光滑自然的变形序列，不出现如上图1和图2中的剧烈收缩直到一个点或者翻转的情况。

三角形通过顶点插值方法从P到Q，需满足,其中矩阵A为仿射变换矩阵，目的让P的图形逐渐过渡到Q的图形，L为平移变换矩阵，通过平移P逐步过渡到Q位置，图形的形状没有变化。在时间t∈ [0,1]某一中间帧的三角形，可由得到。

为保证变形序列的形态，采用SVD分解法。SVD分解法是指把仿射变换矩阵A分解成三个矩阵,,U S V，即A USV= ，U和V为旋转矩阵，S为缩放矩阵。矩阵A的分解如下：

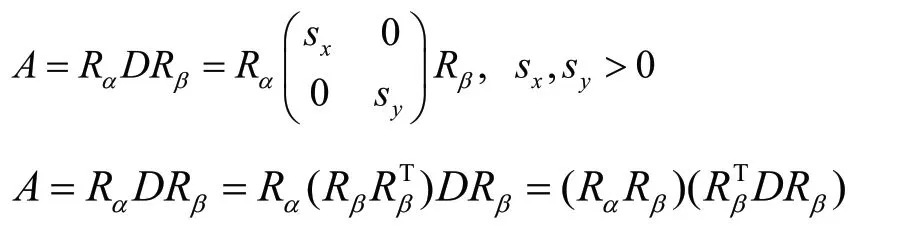
对于中间变形序列t时刻所需构建的三角形，对应的仿射矩阵为，采用线性插值矩阵D，即,得到中间变形序列的矩阵。这种分解方法在计算量不太大的基础上，实现了较理想的渐变效果。

3 本文采用算法

本文采用的方法是综合应用图形渐变对应算法[1]，边角分解与重构算法[7]并基于SVD分解算法[8]和边角插值法避免自交算法[9]对实验图形序列形成光滑、自然、流畅的渐变算法综合。具体步骤如下。

step1:对初始图形IA和目标图形IB采用动态规划模型建立点的对应，在图像渐变序列过程中，始终保持最佳对应状态。

step2：采用边角分解与重构算法，将初始图形进行三角分解，并将对应的顶点进行采用SVD分解算法并进行插值。

step3：将插值后图形采用边角分解与重构算法，进行重构。

step4：采用边角插值法避免自交算法，对图形进行边角的自交检查，并根据设置的阈值ρ0大小，处理图形变形序列。

step5：根据输出的变形序列，是否达到预计效果，调整阈值，重新执行程序，得到合理变形序列图形。

4 仿真实验及分析

算法采用VB6.0计算机程序语言编写，运行电脑采用DELL笔记本电脑，酷睿i5处理器。通过上述算法得到图3、图4和图5。图3是文中图1提到的三角形变形序列中出现的萎缩现象，通过优化算法，萎缩现象得到很好地控制。图4是长角羚羊到短角羚羊变形序列，图形复杂，边角细长，但算法中很好地避免了自交现象。图5是图2中提到的直立树到偏向树自交变形序列，文中算法对自交现象进行了干预，将自交点剔除，实现了无自交情况，并得到了较自然流畅的渐变序列图形。

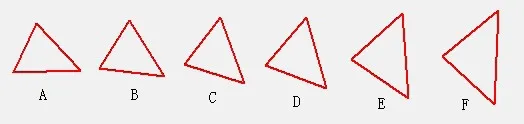
图3 三角形变形序列

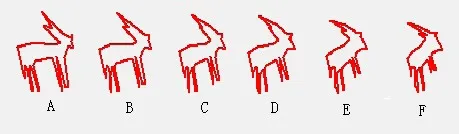
图4 长角羚羊到短角羚羊变形序列

图5 直立树到偏向树变形序列

5 结语

通过算法可以得到较理想的图形渐变序列。该算法综合应用了常用算法，具有一定的实用价值。算法的实现上，需要人工干预，比如阈值的设置。如果得到的图形不满足需要，需重新设置合理的阈值。此外，算法在图形的形态上有一定的要求，尽量让初始图形和目标图形在对应时有较高的相似度，因此在设计相似度量函数时，要综合考虑。对于进行插值的图形，尽量让图形在形态上有较高的相似度，初始图形和目标图形不要有交叉图形，不然在初始阶段，算法很难保证有理想的渐变效果。算法避免自交是舍弃了部分自交点的边和角，难免有一定的不合理情况，这需要算法设计人员再考虑更有效地处理方案，比如可以考虑在自交舍弃处采用更光滑的曲线连接方式，如贝塞尔曲线。希望各位科研人员能够在该算法的基础上，提出更优秀的算法，或弥补算法的不足，得到更合理有效地图形渐变算法。