栎类天然次生林直径结构规律初探

易 烜，朱光玉，王琢玙，张娅妮，黄 靓，陈佳楠

(1.湖南省青羊湖国有林场，长沙 410627； 2.中南林业科技大学，长沙 410004；3.湖南景辉农林生态科技有限公司，长沙 410000)

林分结构是指林分在未遭受破坏的情况下，林分内部存在着一些相对稳定的结构规律，是经营森林的理论基础[1]。林分内各种不同直径林木按径阶大小分布状态形成的林分直径结构，是研究林分结构的基础[1]。林分的直径结构与林分的结构和功能密切相关，一方面林分的出材量表或生长收获量表需要根据林分直径结构来编制；另一方面依据林分直径结构，评估林分产生的经济价值和成效，评价与预测未来林分的直径结构，还可以检查营林技术措施效果等[2]。

栎类是常绿或落叶乔木，系壳斗科，在工业原料、建筑用材、生态修复和绿化环境等方面发挥着必不可少的作用[3]。栎类天然次生林在湖南省境内广泛分布，是本省天然常绿阔叶林的优势树种，经济价值极为可观[4]。但是目前我国栎类经营存在单位面积产量不高、生产力低、经营不合理等问题。研究栎类天然次生林直径结构规律，为指导栎类天然次生林生产经营，提升森林质量发挥着重要作用。

本文以中南林业科技大学芦头实验林场内栎类天然次生林中的甜槠和锥栗为研究对象，调查并研究其直径结构规律，采用Weibull分布函数和正态分布函数分别对学其株数和直径相关关系进行模拟，并且利用卡方检验对模拟结果进行检验，找出较优的拟合函数；采用多项式模型、Logistic模型和Richards模型分别对甜槠和锥栗的株数累积百分数和相对直径关系进行拟合，探讨其直径分布规律。

1 研究区概况

研究区位于中南林业科技大学芦头实验林场境内。芦头实验林场地处平江县的东南面， 113°51′52″ —113°58′24″E， 28°31′17″ —28°38′00″N，属罗霄山脉北端支脉，中山地貌,海拔最高为1 272.5 m，最低为124 m，平均坡度在30°左右;属于亚热带季风气候，光照充足，多年平均日照时数1 930 h，年均降水量为1 450.8 mm。林场经营面积5 308.3 hm2，森林面积5 000.4 hm2，活立森蓄积量37.69万m3，毛竹立竹368.89万株，森林覆盖率94.2%。

芦头林场森林植被系属中亚热带典型常绿阔叶林，植被种类组成丰富、类型多样，珍稀濒危保护植物和地方特色植物品种多,现保存有2 667.6 hm2的天然林，其中的甜槠林原生群落是迄今发现同类型森林中分布海拔最低、面积最大、结构最为完好的森林。

2 数据与方法

2.1 数据采集与整理

2020年9—11月，采用典型取样法，在芦头实验林场栎类天然次生林中设置林分年龄基本一致的样地13块，样地规模为25.8 m×25.8 m。详细调查样地内环境因子和林分因子，对样地内胸径大于5 cm的乔木进行每木检尺，记录其树种、胸径、树高、冠幅、坐标等因子；同时记录样地的经纬度、海拔、坡位、坡度、坡向、土壤类型、土层厚度、群落类型、起源、郁闭度、林龄等。样地调查情况见表1。

2.2 研究方法

直径大小一般以径阶的形式来呈现，直径大小分布对林分的蓄积、断面积和林分株数等林分特征的表达有着十分重要的影响。林分直径结构是林分结构中最基础、最重要的内容,对林分直径分布及其模型的分析与研究有着重要作用[1]。因此，模拟林分直径分布的结果将会影响预测林分未来的收获结果，并影响着不同的森林管理计划实施结果之间的比较结果。制定森林中合理的经营方案，其中最重要的因素是如何根据正确的林分结构来模拟与之对应的林分生长状况[5]。

目前，模拟直径分布规律的方法一般归为两种。其一是相对直径法，它通过计算林分的相对直径及株数累积百分数，由此绘成株数累积百分数的曲线图，进而研究探寻林分的直径分布规律[6]。如邓坤枚等[7]采用直方图法分析生长在长白山地区云冷杉林胸径分布范围及各径阶的林木株数随着径阶的变化而变化；王金山等[8]研究塔里木河流域胡杨各胸径段在样带中所占的百分比，胡杨在流域内的分布也产生了相应的变化,为制定修复塔里木河流域生态环境的方案提供了客观科学的依据。

表1 样地的基本情况样地号海拔/m坡位坡度坡向土层厚度/ cm郁闭度林分年龄/a株数密度/(株·hm2)平均胸径/cm平均高/m优势高/m1999上部斜坡阴850.83631 26722.8311.7117.321 049上部斜坡阴900.88302 43617.2512.2115.831 012上部斜坡阳650.83582 36817.0711.8216.14934上部陡坡阴670.83511 26325.5015.5515.75888上部陡坡阴680.78461 21524.4213.2315.16995上部斜坡阴790.90401 06521.2412.7415.97933上部陡坡阳700.70411 49921.3013.3915.08 955上部陡坡阳950.778180129.6212.3917.19 915上部陡坡阴520.69511 27320.8212.0414.810963上部陡坡阴780.78522 17418.3614.0617.911968脊部陡坡阴850.83522 03519.0912.5116.412989上部陡坡阴750.79621 94621.0913.9517.0131 025上部急坡阴870.794499825.3113.4419.4

另一种方法是概率分布函数法，它根据林分直径分布的具体形状特征和变化规律，选取不同的概率分布函数来模拟林分直径分布，成为众多国内外学者科研的重点对象。近年来，用于描述林分的直径分布的理论概率密度方程多种多样，如正态分布[9]、Weibull分布[10-14]、对数正态分布[15]、Jonson’s SB[16]等，其中Weibull分布用的最为普遍。如孟宪宇等[17]以Weibull分布函数为基础，成功构造了林分直径分布收获预测模型, 并且运用参数回收技术来预估函数的分布参数，较好地对辽宁省抚顺地区的长白落叶松人工林建立收获预估模型；亢新刚[18]通过调查长白山金沟岭林场境内的云杉和冷杉针叶混交林，发现运用Weibull分布函数与负指数分布函数分析伐林区的针叶混交林直径结构，能取得较理想的结果；Sarkkola[19]针对分布于欧洲地区生长在泥炭地中的赤松(Pinussylvestris)，用Weibull方程来研究描述树龄在29～66 a间的赤松林分结构变化情况；陈希英[20]应用 Weibull 分布等 5 种概率密度函数拟合突脉青冈天然林中4个主要树种的直径分布函数，并计算了偏度、峭度等特征数。

2.2.1 概率分布函数法

本文采用正态分布函数和Weibull分布函数，模拟栎类天然次生林的直径结构，并比较分析这两种方法的模拟结果，进而分析芦头实验林场中栎类天然次生林的直径分布规律。

1)正态分布。其公式为：

(1)

2) Weibull 分布。Weibull 分布的概率密度函数为:

参数c是Weibull分布密度函数中最具有实质意义重要参数，其数值不同其分布曲线形状即不同。当a=0，c<1时，函数为反J型分布函数；当13.6 时，函数由正偏分布逐渐趋于左偏。

3)精度检验。卡方检验是数理统计中精度比较高的方法，操作便捷容易。在Forstat软件中，本文采用的卡方检验以林分总体为对象，对芦头实验林场栎类天然次生林的直径分布拟合结果进行检验，判断其直径分布类型。

2.2.2 相对直径法

研究对比不同平均直径、不同株数的林分，采用相对直径法研究林分的直径结构规律更加方便准确。整理筛选栎类天然次生林每木调查结果，用公式(3)和(4)计算出林分平均直径和相对直径。

(3)

Ri=di/Dg

(4)

式中：di为第i株林木的胸径；N为林分内林木总株数；Dg为林分平均直径；Ri—林分相对直径。以径阶为单位，分径阶列出林木株数，按径阶计算出株数累积百分数，绘制株数累积百分数曲线。在本文中，采用传统的多项式模型、Richards模型和Logistic模型对芦头实验林场中栎类天然次生林的株数累积百分数与相对直径进行拟合。

1)三次抛物线模型

y=a+bx+cx2+dx3

(5)

式中：x为自变量，即相对直径；y为因变量，即株数累积百分数；a，b，c和d为方程参数。

2)Richards模型

y=A(1-e-rt)c(A，r，c>0)

(6)

该方程是Richards基于Von Bertalanffy的生长理论扩展而来，通过分析植物生长后，认为m>1是主要的应用范围，故把Bertalanffy方程中参数m的取值范围扩大到m>0[21]。

3)Logistic 模型

(7)

式中：A为树木生长的最大值参数，A=ymax；m为与初始值有关的参数；r为内禀增长率(最大生长速率)参数[21]。

4)模型精度检验指标。模型的精度检验及选型，采用确定系数(R)作为指标，确定系数越接近于 1，模型模拟效果越好[21]。

3 结果与分析

3.1 林分直径结构分析

通过调查，栎类天然次生林中主要树种为甜槠、锥栗，其中甜槠131株、锥栗84株，分别将同一树种按胸径4 cm为一径阶整化。经数据筛选和整理，甜槠、锥栗的株数分布和株数累积分布曲线，见图1，图2。

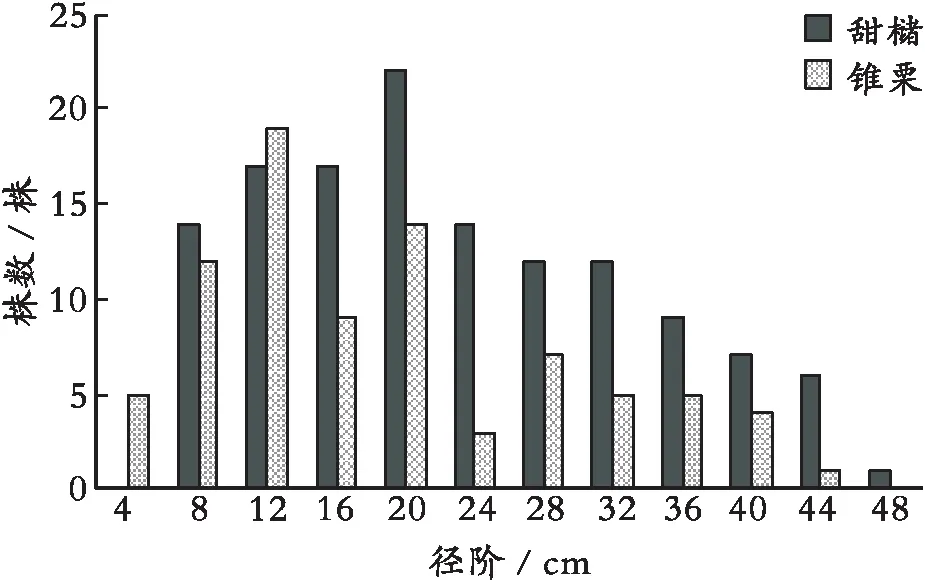
图1 直径分布图

图2 株数累积百分数曲线图

甜槠直径分布主要集中在径阶20 cm处，紧接着是12 cm和16 cm处，其次是8 cm和24 cm处，其它径阶株数分布较少，符合一般的林分直径分布规律；锥栗直径分布大多集中于12 cm处，然后是20 cm处，再是8 cm处，其它径阶株数分布较少，比较符合一般的林分直径分布规律。

甜槠、锥栗相对直径与株数累计百分比的变化规律，与“不论树种、年龄、密度和立地条件如何，其林分平均直径(Dg)在株数累积分布曲线上所对应的株数累积百分数的位置在55%～64%，一般近于60%处的结论是一致的[1]。

3.2 株数累积百分数与相对直径关系拟合

运用对数、线性、多项式、倒数等方程与相对直径拟合得出的株数累积百分数估计值，其结果一般不在0～1之间，这类结果既不符合客观实际，也没有生物学意义。本文运用Forstat 软件，选用符合客观实际且具有生物学意义的Richards模型和Logistic模型及传统多项式模型中具有代表性的三次抛物线模型，对芦头实验林场内的栎类天然次生林进行拟合，并对不同模型的拟合结果进行分析，模型拟合确定系数见表2。

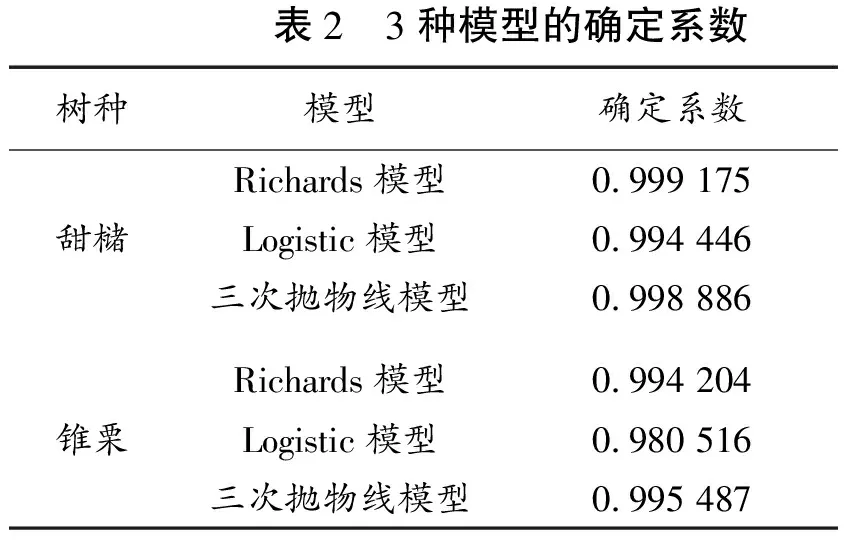
表2 3种模型的确定系数树种模型确定系数Richards模型0.999 175 甜槠Logistic模型0.994 446 三次抛物线模型0.998 886 Richards模型0.994 204 锥栗Logistic模型0.980 516 三次抛物线模型0.995 487

对于甜槠来说，三种模型的确定系数都在0.99以上，系数水平很高。甜槠在3种不同模型下，比较分析累积分布百分数观测值与估计值(表3 )，结果表明 Logistic模型的最大累积株数百分数非常接近于1，Richards 模型和三次抛物线模型的最大株数累计百分数都大于1，不符合生物学意义。

对于锥栗来说，三种模型的确定系数都在0.98以上，系数水平很高，Logistic模型的确定系数略小于Richards 模型和三次抛物线模型的值。锥栗在3种不同模型下，比较分析累积百分数观测值与估计值 (表3)，结果表明Richards 模型的最大累积株数百分数最趋近于1，Logistic模型的最大累积株数百分数也趋近于1，略小于Richards 模型；但三次抛物线模型的最大株数累计百分数大于1，不符合生物学意义。

表3 株数累积百分数观测值与估计值的对比树种观测值模型估计值Richards Logistic三次抛物线0.106 870.108 5110.151 6260.097 9020.236 6410.234 0930.239 3830.246 2500.366 4120.377 3510.356 7550.385 7900.534 3510.516 9350.494 6050.514 9820.641 2210.640 8040.633 8180.632 289甜槠0.732 8240.744 3900.754 540.736 1700.824 4270.827 6650.846 1510.825 0860.893 1300.892 8310.908 8770.897 4980.946 5650.942 8760.948 8610.951 8670.992 3660.980 8020.973 1980.986 65511.009 2720.987 5971.000 3200.059 5240.0810 980.135 3510.0432 070.202 3810.224 9260.230 3890.241 0920.428 5710.388 8040.363 190.408 2310.535 7140.540 8810.518 970.547 6880.702 3810.667 9250.668 2270.662 532锥栗0.738 0950.767 7940.785 9370.755 8280.821 4290.843 4010.865 3130.830 6420.880 9520.899 2650.913 350.890 0410.940 4760.939 8790.940 540.937 0910.988 0950.969 0880.955 350.974 85810.989 9380.963 2491.006 410

比较三种模型，可得到甜槠最适合Logistic模型，而锥栗最适合Richards 模型。通过分析各个模型估计值与实测值的结果对照图(图3和图4)，亦能得到与上述结论相似的结论。

3.3 株数与直径的相关关系模拟

根据栎类天然次生林直径结构的特点，采用了正态分布和Weibull 分布分别对甜槠林和锥栗林直径结构进行拟合。利用Forstat软件，模拟并检验甜槠林和锥栗林的直径结构情况，模拟和检验的结果见表4。

表4 2种分布模拟及检验结果表分布函数树种卡方是否服从正态分布甜槠11.753 800 是锥栗23.721 830否Weibull分布甜槠7.352 755是锥栗14.038 713 是

图3 甜槠各个模型估计值与实测值对照图

图4 锥栗各个模型估计值与实测值对照图

表4可知：正态分布的卡方检验值比Weibull分布的卡方检验值大，Weibull分布的卡方检验值约为正态分布的卡方检验的2/3，说明Weibull分布对甜槠林和锥栗林直径结构分布的模拟效果比正态分布要好；甜槠林的卡方检验值小于锥栗林的卡方检验值，说明甜槠林直径结构分布的模拟效果比锥栗林要好。正态分布对甜槠林和锥栗林直径结构的拟合效果不理想，卡方检验值均较大，甜槠林的卡方检验值不到锥栗林的卡方检验值一半，且锥栗林直径结构不符合正态分布。Weibull分布对甜槠林和锥栗林直径结构的拟合效果和检验效果均较好，卡方检验值均较小，甜槠林和锥栗林直径结构分布符合Weibull分布，甜槠林的卡方检验值约为锥栗林的卡方检验值一半，说明Weibull分布对甜槠林直径分布的模拟效果比锥栗林直径分布的模拟效果要好。

4 结论

以中南林业科技大学芦头实验林场13块样地内栎类天然次生林为研究对象，选取甜槠和锥栗两种主要树种，利用Excel软件和Forstat软件研究栎类天然次生林直径结构规律，得到的结论如下：

1)分析不同立地条件下的13块样地内的甜槠和锥栗林分直径结构，符合一般的林分直径分布规律，立地条件的差异对直径分布无明显影响。本研究中13块样地之间的立地条件、年龄和密度各不相同，海拔相差最大是140 m，坡位有上部和脊部2种，坡度有斜坡、陡坡和急坡3种，坡向有阴、阳2种，土壤厚度相差最大是43 cm，郁闭度相差最大是0.21，林分年龄相差最大是51 a，株树密度相差最大是1635株/hm2。甜槠直径分布主要集中在径阶20 cm处，而锥栗直径分布大多集中于12 cm处，符合一般的林分直径分布规律；甜槠、锥栗相对直径与株数累计百分比的变化规律，与参考文献[1]的结论是一致的，立地条件的差异对直径分布无明显影响。

2)通过分析，甜槠更适Logistic模型，而锥栗更适合Richards模型。采用Richards模型、Logistic 模型和三次抛物线模型拟合栎类天然次生林直径结构，结果表明：Richards模型与Logistic模型对比三次函数而言，不但在精度上更胜一筹，而且有着三次函数所不具备的生物学意义；利用模型预测累计株数百分数时，预测值在0～1只有Logistic 模型，预测值中最大值>1的有三次函数和甜槠Richards模型。

3)对于栎类天然次生林研究，采用Weibull分布函数模拟其株数与直径的关系效果更好。利用Weibull分布函数和正态分布函数2种函数，分别模拟甜槠和锥栗的株数与直径的相关关系，分析结果显示两种函数对甜槠的模拟效果均较佳，两种函数用于模拟甜槠的效果均较理想，且Weibull分布函数较优；正态分布函数模拟锥栗的效果不理想，Weibull分布函数较优。

本文通过研究中南林业科技大学芦头实验林场栎类天然次生林的直径结构规律，得到了较为理想的结果，可为预测栎类天然次生林直径结构和研究栎类天然次生林森林经营及森林质量提升提供参考依据。