一种基于矩阵乘积态的一维量子几何纠缠算法

陈爱民，赵毅婕，刘东昌，苏耀恒

(西安工程大学 理学院，陕西 西安 710048)

0 引 言

自从朗道提出针对二级相变的对称破缺理论以来，多体系统中的量子相变研究一直是凝聚态物理的研究热点[1-3]。量子相变是由量子涨落占主导地位而引起的一种量子效应。近年来，量子信息科学取得的惊人进展，使人们对多体系统中量子相变研究更加深入。如今，在量子信息中用于分析量子相变的不再是可观测的物理量，如比热容、磁化率等，而是直接量化多体系统的波函数基态性质的量子纠缠[4]、保真度[5]等。实际上，量子纠缠可以用来量度指定系统各部分之间的量子关联。由于量子涨落，基态波函数的内部结构在相变点历经了剧烈变化。显然，系统的性质是纯粹由基态希尔伯特空间的几何性质决定的，无论量子多体系统中是否存在可观测的序，量子纠缠都可以用于探测量子相变[6-8]。

用于度量量子纠缠的方法已经在各种不同的系统中进行了大量的测试，其中包括量子Concurrence[9]、von Neumann熵[10]、Renyi熵[11]等，都被证明用于探测量子相变是可行的，甚至有些度量量子纠缠的方法不依赖于模型，是普适的。以上方法基本上是针对于局域的部分纠缠度量，最近人们提出了多体系统中的一种全局纠缠度量的方法——几何纠缠[12]。这种方法本质上是具有几何意义的，与给定的纯态和一组完全分离的乘积态之间的距离相联系。因此，多体几何纠缠的奇异行为揭示了更为丰富系统的量子临界行为，在许多系统中也都得到了验证。

就数值模拟而言，人们也一直在发展不同的算法，用以计算不同系统、不同尺度下的全局几何纠缠[12-15]；WEI等用解析法计算了XY模型的几何纠缠，发现几何纠缠和自旋关联之间的深层次联结[12]；ZHANG等在XXZ模型中首次实现了量子几何纠缠的实验模拟[13]；ORS等应用矩阵乘积态(MPS)表示方法开发算法，计算了SO(n)双线性双二次型模型的全局几何纠缠，得到了此系统极为丰富的相图[14]。最近，CHEN等利用无限投影纠缠对态(iPEPS)表示方法，开发了针对三腿自旋管子模型的几何纠缠算法，首次确定了自旋为3/2的三腿自旋管子的相图[15]。在计算多体系统的几何纠缠时，最关键的步骤是如何寻找到最接近基态波函数的最大乘积态，并且能够准确度量最大乘积态和基态波函数之间的接近程度。因此，发展更为有效的计算全局几何纠缠算法，对深层次理解量子纠缠和量子相变是非常重要的。本文针对于多体系统的几何纠缠模拟，利用近些年才发展成熟的张量网络表示的无限矩阵乘积态(iMPS)表示方法[16-18]，开发了一种基于变分方法的算法，用以计算一维多体系统中基态的全局几何纠缠。与之前的算法相比，本算法的优势在于能够更快地找到所需要的最大乘积态，并准确计算最大乘积态和基态波函数之间的保真度。将本算法在一维横场中的Potts模型和一维双线性双二次型(BLBQ)模型中进行验证，结果显示对于计算一维多体系统的几何纠缠非常有效。

1 几何纠缠算法

如果纠缠态由2个分开的纠缠对子系统组成，量化其中的纠缠是非常有意义的。几何纠缠是用于度量量子基态波函数和与之最近的乘积态之间距离的物理量；几何纠缠测量的是基态波函数中整体纠缠的大小，是纠缠的一个全局量化。这个量度本质上是有几何意义的，因为几何纠缠与给定的纯态和一组完全分离的乘积态之间的距离相一致。

系统的几何纠缠的值随着系统尺寸的增长呈线性增大，所以很容易定义单位长度上几何纠缠的值。对于一维晶格系统，若把每个格点看作一部分，那么单位格点的几何纠缠可以定义为单点几何纠缠[18]。为了介绍清楚如何测量量子多体系统中的单点几何纠缠，此处考虑一个一般的具有N个部分的归一化状态|ψ(α)〉，其中α表示系统控制参量。实际上，量子态|ψ(α)〉和最接近的N体乘积态|φ〉之间的最大保真度Λmax(α)=maxφ〈φ|ψ(α)〉可以量化|ψ(α)〉的全局多体几何纠缠。此处

|φ〉=⊗as|φi〉

其中:|φi〉表示单个自旋纯态;⊗as表示所有自旋态张量积。全局单点几何纠缠GELS定义为[13]

(1)

如果一个量子态与一个乘积态越接近，则由定义可知最大保真度变大并且GELS变小。因为0<Λmax<1，Λmax越大，系统的纠缠越小。如果纠缠态是由2个分离的纠缠对组成的，那么Λmax就表示这2个纠缠对之间的相似度。因此，可以根据几何纠缠广延的性质给出状态|ψ(α)〉的全局纠缠定义

(2)

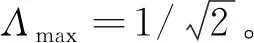
(3)

式中：b是单位格点几何纠缠有限尺寸修正的最大项系数。从量子信息的角度看，一个状态包含的纠缠越多，它的资源也就越多。因此，需要量化量子系统处于临界点附近时的纠缠度。通过纠缠判断量子多体态的性质，将可能会提供一个解决量子多体问题的新视角。

可以利用图1(c)计算出〈ψ|ψ〉对态|ψ〉的归一化，而图1(d)可以计算出单格点约化密度矩阵。为了计算单点几何纠缠GELS，需要计算〈φ|ψ〉，其中|φ〉是一个任意的N体乘积态，每一个部分对应一个格点。因为GELS定义为交叠函数〈φ|ψ〉的极大值，因此，在数值模拟中如何实现取遍所有可能的乘积态|φ〉以计算交叠函数〈φ|ψ〉，显得尤为关键。

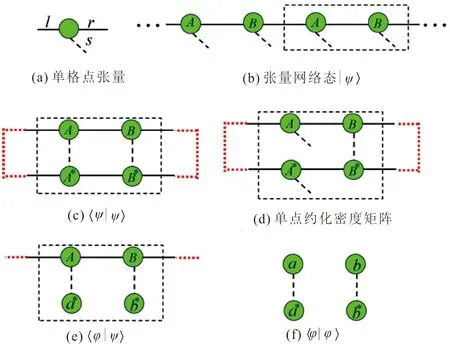
图 1 张量网络表示下的几何纠缠算法Fig.1 Geometric entanglement in the tensor network (TN) representation

的对数对xs(xs∈{as,bs})求导，引入单阶指标张量xs更新过程:

(4)

其中〈φ|φ〉的张量网络表示如图1(f)所示。一旦获得了交叠函数的梯度，则直接可以得到xs的更新

(5)

其中δ表示参数空间的步长。最后，为了获得最好的乘积态|φ〉，使得交叠函数f最大化，重复更新过程直到梯度变为0。这个过程保证了态|ψ〉和|φ〉之间最大的交叠。

2 数值结果

2.1 Potts模型

一维量子模型具有极为丰富的临界性质，是深入理解量子临界现象的最好选择。而一维模型中作为一种量子统计模型，Potts模型一直被人们当作算法验证的首选平台。因此，选择了一维横场中的q态量子Potts模型[19]，其哈密顿量可表示为

(6)

式中：λ表示横向磁场;Mx/z,p(j)(p∈[1,q-1])是格点j处的q态Potts自旋矩阵。q态Potts自旋矩阵写作

(7)

式中：Iq-1是(q-1)×(q-1)单位矩阵；Mx,p=(Mx,1)p。此模型哈密顿量具有Zq对称性[20]。如果哈密顿量的基态不再具有Zq对称性，系统经历了Zq对称性破缺，也就是发生了量子相变。特别地，当磁场在λc=1前后变化时，q态量子Potts模型经历的是一个有序相和无序相之间的量子相变。这个量子相变起源于Zq对称性破缺，并将导致有序相中长程序的出现和q个基态的简并。

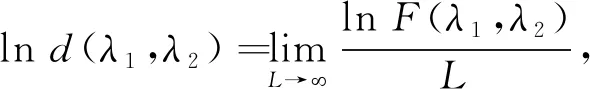
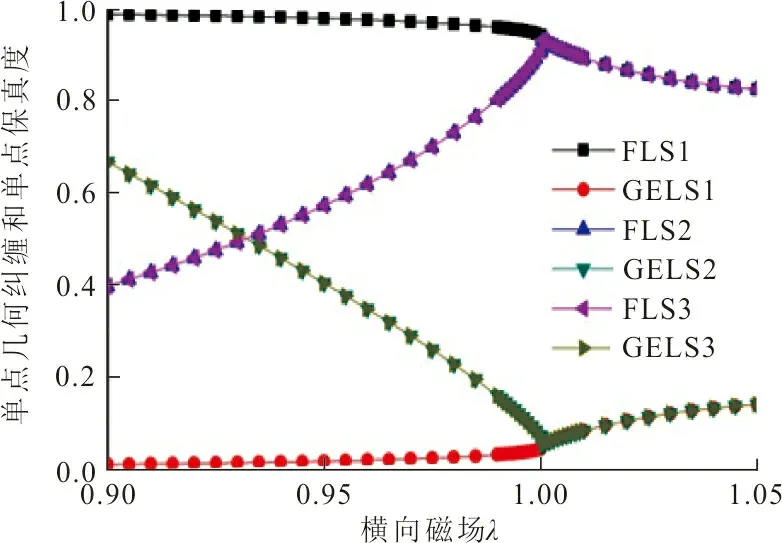
图 2 三态Potts模型几何纠缠GELS和保真度FLS随λ的变化Fig.2 Variation of geometric entanglement per lattice site (GELS) and fidelity per lattice site (FLS) of three-state Potts model with λ

从图2可以看出:单点格点保真度FLS在对称破缺相中出现了2个不同的值，从而分为2支;在λ=1之后2分支合并，从而在λ=1处单点保真度FLS曲线出现奇异。此奇异点对应着量子相变点。说明单点保真度FLS不但确定了模型的相变点，而且也确定了有序相中的对称破缺。对于单点几何纠缠GELS，其性质和单点保真度FLS类似。单点几何纠缠GELS在对称破缺相中也出现了2个不同的值，从而分为2支；在λ=1之后2分支合并，从而在λ=1处单点几何纠缠GELS曲线出现奇异。此奇异点标明了量子连续相变点。所得到的相变点λc=1和单点保真度FLS是相同的，也符合解析解所确定的相变点位置。可见，文中所开发的计算系统几何纠缠的算法，在用来刻画Potts模型量子相变点时和普适的保真度方法是相同的。

2.2 BLBQ模型

为了更全面地验证本算法的正确性，选择了更为复杂、相图更为丰富的一维自旋为1的BLBQ模型。前人针对此模型的各种物理量已经进行了详细的研究，如不同的纠缠量和边缘态的能隙等[23]。已有的研究结果表明，BLBQ模型具有特殊的自发二聚化特性[24]。自旋为1的BLBQ模型的哈密顿量可以写成

(8)

式中：Si是格点i的自旋1算符；J表示最近邻自旋之间的反铁磁相互作用；α是双二次项相互作用系数。BLBQ模型在AKLT点(α=1/3)是可以得到解析解的，其基态是有最低激发能隙的VBS(valence-bond-solid)态。模型在Takhtajan-Bubujian点(α=-1)和Uimin-lai-sutherland点(α=1)也是有解析解的，这2个点都有无能隙的基态。对于α<-1，系统是自发有能隙的二聚化态，而对α>1是没有能隙的三重态。对于在二聚化态和三重态之间的-1<α<1，系统处于Haldane相。

图3计算了BLBQ模型系统的单点几何纠缠和单点保真度随双二次项相互作用系数α的变化。数值计算中所采用的截断维数χ=32。

图 3 BLBQ模型几何纠缠GELS和保真度FLS随α的变化Fig.3 Variation of geometric entanglement per lattice site (GELS) and Fidelity per lattice site (FLS) of the BLBQ model with α

从图3可以看出:随着参数α从-2增大到2，单点保真度FLS在α≈-1.05处达到最大值，在α=1处达到最小值。这2个位置对应着从自发二聚化相到Haldane相，Haldane相到Trimerized相的2个相变点的位置。从单点几何纠缠GELS来看，单点几何纠缠先缓慢减小，在α=-1.05处达到最小，随后迅速增大，在α=1处达到峰值。此变化性质正好和保真度所标定的相变点是符合的，并且较为接近于精确的相变点位置，说明本文中所开发的几何纠缠算法在用于刻画更为复杂的双线性双二次型模型的量子相变点时是正确的。

3 结 语

为研究多体系统中的全局量子几何纠缠和量子相变，本文利用多体系统的张量网络表示，开发了一种基于变分的计算系统量子几何纠缠的算法。通过此算法计算了三态Potts模型和BLBQ模型的单点几何纠缠，并且和系统基态的单点保真度结果相互验证。结果表明，本算法对计算多体系统中的全局量子几何纠缠是可行的、有效的。单点几何纠缠的行为在系统相变点处出现奇异性，可以用于刻画出量子相变点。在对称破缺相中，单点几何纠缠的分叉行为又直接确定了系统对称破缺的性质。计算结果与普适的单点保真度方法是吻合的。因而，本文开发出的系统全局量子几何纠缠算法，为多体系统的量子纠缠和量子相变研究提供了一个全新而有效的技术手段。