石蜡-泡沫铜复合相变蓄热材料热特性的研究 *

宋瀚文，王子龙，闫勤学，朱孟帅，张 华

(1.上海理工大学 能源与动力工程学院，上海市动力工程多相流动与传热重点实验室,上海 200093；2. 南京汽轮电机(集团)有限责任公司,南京 210000)

0 引 言

相变蓄热材料利用潜热储能，具有能量密度高，储能/放能过程近似等温等优点，是太阳能储热系统研究的热点[1]。但是纯相变蓄热材料大多导热率低，限制了其在工程上的应用，提高相变材料的导热率，强化其传热能力，是研究的重点。目前常用的方法有翅片管[2]，相变材料微胶囊[3]，添加金属环，膨胀石墨[4]等以及将相变材料填充入多孔基质，如泡沫金属等。

加入泡沫金属一般采用导热率高的铝、铜和镍。Jourabian 等[5]使用Al2O3作为多孔基质，结果表明，Al2O3作为基质可以有效增强其导热率。Xiao等[6]建立了考虑试样与临近表面接触热阻的试验测量系统，测量了石蜡-泡沫金属复合相变材料的有效导热率。此外，Xiao等[7-8]对比了真空条件与非真空条件下，石蜡注入比例对复合材料导热率的影响。结果表明，真空注入条件下，复合相变材料的导热率为纯石蜡的3倍。同时研究发现，泡沫金属的加入，使相变温度发生了轻微变化。于航等[9]搭建了填充石蜡-泡沫金属的实验台进行熔化蓄热实验。结果表明传热得到明显强化且传热温差越大,自然对流越明显,蓄热时间越短。程文龙等[10]以石蜡-泡沫铝复合材料为研究对象，提出了一种平衡储能能力和传热性能的方法。

多孔基质复合相变蓄热材料的模拟常采用构建多孔结构的孔尺度法。Zhang等[11]建立了泡沫铝中固液相变的三维数学模型，对孔隙率由下至上线性变化的泡沫金属复合材料进行数值研究。结果表明，泡沫金属通过增强底部边角的传热能力，增强了系统的蓄热率。魏高升等[12]基于泡沫金属基3D微观结构，采用W-P模型重点分析了泡沫金属复合相变材料有效导热系数与孔隙率和孔径的关系。研究结果表明该模型能够精确预测泡沫金属复合相变材料的有效导热系数。Hu等[13]建立了可视化的实验，研究了泡沫金属对相变材料的强化效果，采用修正Kelvin模型对泡沫金属进行了数值模拟。研究表明，泡沫金属可以显著提高相变材料的导热率，熔化时间较纯石蜡减少了45%，最大温差减少了83.3%，实验结果与Kelvin模型理论值吻合。Li等[14]建立了六面体金属骨架模型，数值模拟了NaNO3与泡沫铜的复合相变蓄热材料在储能方面的应用。结果表明，当复合材料仍为固态时，传热系数提高了28倍，当复合材料为液态时，热传导及自然对流相结合，使复合材料的传热系数提高了3.1倍，复合材料的熔化和凝固时间都大大缩短。Feng等[15]建立了简化的十四面体的泡沫金属三维模型，通过对称简化，模拟分析了泡沫金属对翅片的强化散热作用。证明了泡沫金属与相变材料之间温差较小，可以采用单温度热平衡模型，并且模拟证实了自然对流的作用不可忽略。

由于相变蓄热材料在熔化过程中，同时存在导热与自然对流，且熔化过程大部分以导热为主，底部尤为明显，相关研究仍然不多。因此，本文建立了可视化的实验装置，研究复合相变蓄热材料在熔化过程中固液界面的变化过程。同时，分析了泡沫金属对石蜡熔化过程的强化机理，并基于焓-多孔介质模型，对复合相变蓄热材料的熔化过程进行了数值模拟，为进一步研究多孔基质复合相变材料热特性提供了理论依据。

1 实验描述

1.1 实验系统

本文研究的多孔基质复合相变蓄热材料由泡沫金属铜和石蜡复合而成。石蜡填充在铝制半圆柱空腔内(R25 mm×90 mm，壁厚2 mm)，填充高度为65 mm。泡沫金属铜孔径为5PPI，高为10 mm，填充率为15%，与铝制容器壁面紧密接触，故不考虑接触热阻。

石蜡的导热系数由热物性测试仪(hotdisk)获得。差示扫描量热仪(DSC)测量曲线如图1所示，测量过程由45 ℃加热到110 ℃，加热速率为5 ℃/min，得到了石蜡的相变温度，比热及相变潜热。材料的热物性如表1所示。

图1 纯石蜡差示扫描量热仪(DSC)曲线Fig 1 Differential scanning calorimeter (DSC) curves of pure paraffin

表1 纯石蜡的热物性

实验系统由直流电源、测试部分和数据获取部分组成，如图2所示。电加热板(测量精度为±0.2 W)固定在铝制空腔侧面及底面，外部为聚四氟乙烯夹板(厚度50 mm)，用以固定电加热板并减小热损失。装置正面为玻璃视窗，便于观察熔化过程中固液界面的变化。在实验过程中，环境的初始温度为298 K。直流电源并联连接电加热板，以恒定热流42 W加热。实验中用铂电阻对石蜡内部温度进行测量，腔体底部至上部依次布置测温点1～4，分别距底面高度为10、30、50和60 mm安捷伦测试仪每1 s记录一次温度变化。

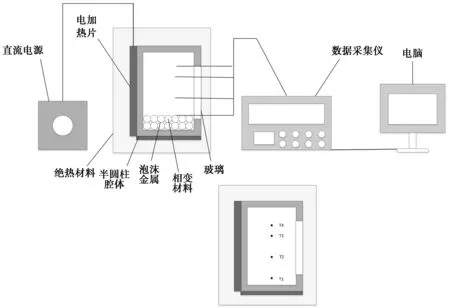
图2 石蜡-泡沫金属复合相变蓄热材料性能测试装置系统图Fig 2 Performance testing device system diagram of paraffin/metal foam composite PCMs

1.2 实验误差分析

温度测量系统由测温传感器、数据采集仪和电脑组成，实验台的误差分析由Kline和Mcclintock提供的方法给出[16]。本实验采用PT-100铂电阻作为测温传感器，精度为±0.15℃。使用的数据采集仪为Agilent34972A数据采集仪，测量精度为0.0004%。因此温度的最大相对误差为：

(1)

2 模型及研究方法

2.1 构建泡沫金属模型

模拟重建了复杂的泡沫金属几何模型，将泡沫金属铜(图3)简化以球体为中心的十四面体，模型采用三维软件构建。

图3 泡沫金属几何模型(a)光学照片(b)理想单元几何结构模型Fig 3 Geometry model of metal foam: (a) optic image; (b) ideal element geometry model

2.2 数值计算模型

为节省计算时间，考虑到模型在y方向对称，取x>0区域为计算域。在计算域内，填充的泡沫金属包含两层金属球，共计26个。图4为该模型泡沫金属的网格划分，为了清晰图4没有显示石蜡的网格。

图4 石蜡-泡沫金属复合相变蓄热材料模型Fig 4 Paraffin/metal foam composite PCMs model

模拟计算域为石蜡填充部分，忽略热辐射的影响。聚四氟乙烯包裹腔体的底部、后部，仅考虑电热板提供的恒定热流，热流边界为5 200 W/m2。腔体内石蜡液面与空气接触，设为对流边界，对流系数为30 W/(m2·K)。模型采用对称简化，侧面为对称边界。正面玻璃与外部空气自然对流换热，对流系数为20 W/(m2·K)。模拟中做出以下假设：

(1)石蜡和泡沫金属的热物性不随温度改变，为常数。

(2)石蜡密度采用Boussinesq假设，忽略熔化过程体积膨胀

(3)研究温度范围内，液态石蜡为不可压缩的牛顿流体，且为层流流动。

多孔介质的相变传热由液相石蜡的连续方程和动量方程以及相变材料的能量方程控制：

3.提高农村幼儿园绘本阅读活动的多元化。农村幼儿园老师应灵活使用游戏式、表演式、亲子式等多种绘本阅读模式。幼儿园老师可以根据绘本阅读教材内容来创造性的设计一些趣味性和互动性强的游戏，帮助幼儿更加准确的理解和把握绘本阅读材料角色的感情和特征，活跃幼儿绘本阅读氛围，提高幼儿绘本阅读的注意力以及培养幼儿绘本阅读的兴趣爱好；幼儿园老师可以先让幼儿独立阅读和了解绘本内容，随后让幼儿扮演绘本材料中不同的角色，幼儿相互配合共同完成绘本所讲述的故事，有利于锻炼幼儿的语言表达能力、记忆力以及团结合作能力等等。

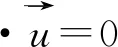
(2)

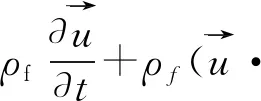
(3)

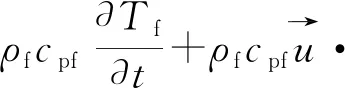
(4)

式中：脚标f表示相变材料；u为速度，m/s；k为导热系数，Wm-1K-1；t为时间，s；g为重力加速度，m/s2；Tm为相变温度，K；ρ为密度，kg/m3；β为热膨胀系数，1/K；μ为动力粘度，Ns/m2；cp为比热容，J/kgK；L为相变材料的潜热，J/kg；fl是相变材料的液化分数。

公式(3)中的系数A与液体分数有关，表达式如下：

(5)

(6)

C是一个非常大的数，S是一个避免分母为0的微小量。

模型中，动量方程选择三阶格式，能量方程选择二阶迎风格式。通过对不同时间步长的测试，在综合考虑计算时间和准确性后，时间步长定为0.02s。每个时间步长内的连续性方程，动量方程，能量方程的残差收敛判断标准分别为10-5，10-5和10-6。选取290w，410w两种数量不同的网格进行网格独立性验证，对比测温点T2温度随时间的变化。如图5所示，两组网格的预测值均方根误差分别为1.79%和1.95%，且290w的温度曲线与实验相吻合。因此，本文选择290w数量的网格模型。

图5 网格独立验证Fig 5 Mesh independency study

2.3 瑞利数(Ra数)

以英国科学家Rayliegh命名的瑞利数是评价自然对流强度的重要参数。假设石蜡熔化过程中，密度不变，则瑞利数可由下式计算得出[17]：

(7)

式中：ρ为密度；g为重力加速度；α为体膨胀系数；W为腔体当量边长，mm；Th为高温壁面温度；Tm为相变温度；μ为动力粘度；a为导温系数，m2/s。

2.4 误差分析

(8)

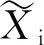
3 结果与分析

3.1 温度场分析

纯石蜡和复合相变蓄热材料在熔化过程中的温度变化如图8所示。由图1可知，石蜡的相变过程发生在一个温度范围内(348～365 K)。在这个范围内，石蜡发生相变，释放潜热，整个过程包括固相的显热蓄热、相变阶段的潜热蓄热以及液相的显热蓄热。当温度上升至350 K左右时，石蜡升温速度加快，这是因为石蜡熔化后，液相石蜡出现自然对流，伴随固体沉降扰动加速了内部传热，使得各测温点温度迅速上升。

对于纯石蜡的熔化过程，t=640 s前传热过程以导热主导，T1温度高于T2、T3和T4，且T2、T3和T4温度基本相同。640 s后，随着熔化过程的进行，自然对流在传热过程中的影响逐步加剧。在浮升力的作用下，热流体向上运动冷流体向下运动，形成自然对流，进而加速上部石蜡熔化。测温点T4、T3、T2的温度依次超过T1，顶部温度高于底部且上下温差逐渐增大，对流强度增大。t=901s时熔化结束，T4温度为418 K，高于其余各点，上下部温差为31 K。

同纯石蜡实验相比，泡沫金属的加入，加速了热量从加热面向内部传递速率，强化了底部导热作用，进而提高了石蜡熔化速率。由图6可知，泡沫金属铜使腔体底部对流受阻，T1受到的对流影响减弱，温度未出现明显振荡。腔体底部导热为主导，强化效果显著，T1温度明显升高。熔化结束时，T1温度为402 K，同纯石蜡相比上升15 K。T2、T3位于中部，同时存在导热与对流作用。600 s后，T2、T3温度均略高于纯石蜡，表明整体仍呈现强化效果。T4位于顶部，对流为主导，因为纯石蜡对流强度更高，故700 s前纯石蜡T4温度更高。700 s后，泡沫金属实验T4温度略高，由下述原因所致：一方面由于固/液界面下降，纯石蜡实验由重力驱动的自然对流相应地减少；另一方面复合相变蓄热材料实验熔化速率更快，中下部液态石蜡温度更高，导热作用加强了复合相变蓄热材料实验上部温度。t=700 s时，T4、T3、T2温度依次超过T1，表明液相区内自然对流已经形成，较纯石蜡延迟约60 s。泡沫金属的加入，使得内部温度分布趋于一致，上下部温差减小。t=870 s时，熔化结束，熔化时间减少了3.44%，上下部温差为16 K，较纯石蜡减少48.39%，即泡沫金属能有效减少热量不均的问题。

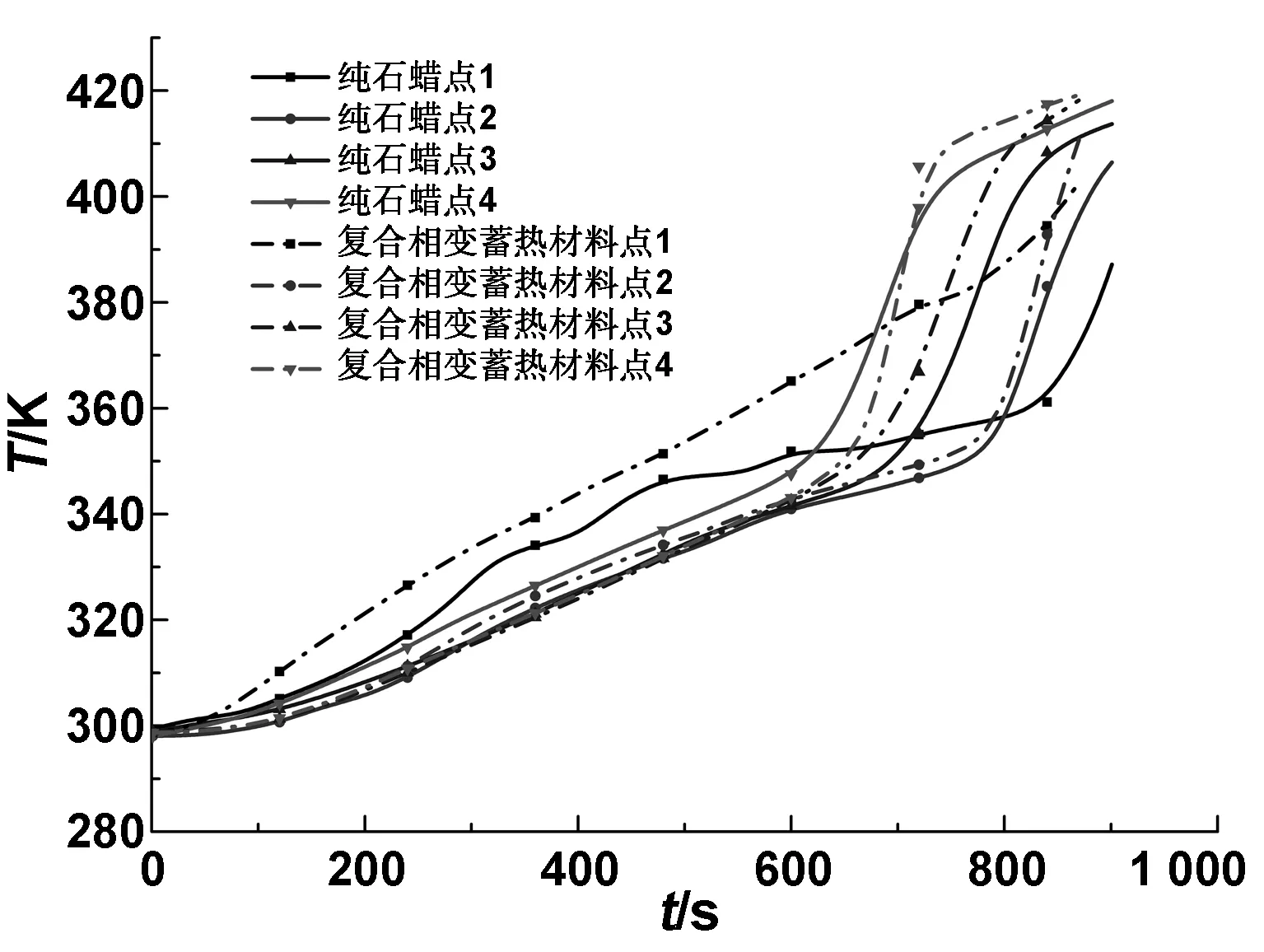
图6 纯石蜡与复合相变蓄热材料在熔化过程中的温度变化Fig 6 Temperature change of pure paraffin and composite PCMs during melting

3.2 数值模拟

图7和图8示出了实验与模拟熔化过程的固/液界面变化对比。在Boussinesq假设下，液态石蜡虽忽略体积膨胀，但是仍考虑了密度差所产生的浮升力。由图可知，t=600 s时，靠近加热壁面的底部与侧面石蜡首先熔化，固液界面与加热面近似垂直。在固态与液态密度差的影响下，液态石蜡体积膨胀，加热壁面附近高温的液态石蜡向上流动，固液界面处低温液态石蜡向下流动，在重力作用下形成自然对流。随着熔化过程的进行，液态石蜡沿着上界面向容器的中心移动，液相区逐渐增大。腔体内上部熔化速率大于下部熔化速率，相变界面逐渐倾斜，石蜡液化速率加快。t=780 s时，上部液态石蜡完全包裹固态石蜡并呈三角状，表明右上方形成涡流区。

图7 纯石蜡熔化过程的实验和数值分析Fig 7 Experimental and numerical analysis of the melting process of pure paraffin

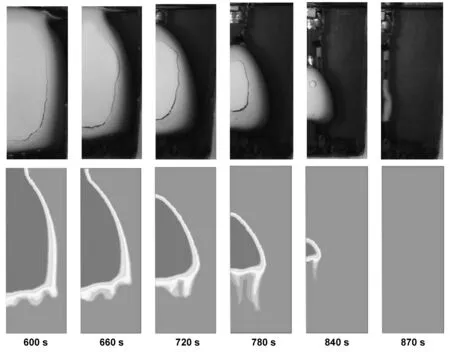
图8 复合相变蓄热材料熔化过程的实验和数值分析Fig 8 Experimental and numerical analysis of melting process of composite PCMs

模拟结果显示t=882 s时，纯石蜡模型熔化结束，较实验结果快了19s。t=842 s时，复合相变材料模型熔化结束，较实验结果快了28 s，模拟与实验结果吻合较好。与纯石蜡模型相比，在同一时间，复合相变蓄热材料模型的熔化速率更高，且底部固液界面上升。这表明泡沫金属能显著强化底部导热，底部温度高于纯石蜡。两者模拟的过程均快于实验结果，原因是在实际实验中，绝热材料会吸收一部分热量，产生一部分热损失。且模拟计算中材料热物性的数值与真实值有偏差，如粘度、热膨胀系数等，特别是忽略了液态石蜡的体积膨胀，会对模拟结果造成一定程度的影响。

图9为模拟与实验测温点2的误差对比，由图可知，实验的终温均高于模拟终温。原因是实验进行至800 s后，中上部石蜡熔化为液态，对流占主导地位，处于由层流至湍流的过渡状态，因此会有误差。RMSE均方根误差分别为0.0223和0.0179。

图9 纯石蜡与复合相变蓄热材料实验和模拟温度对比曲线Fig 9 Experiment and simulation contrast curves of pure paraffin and composite PCMs

3.3 自然对流强度分析

基于瑞利数，本文对石蜡在融化过程中自然对流的强弱变化进一步分析。

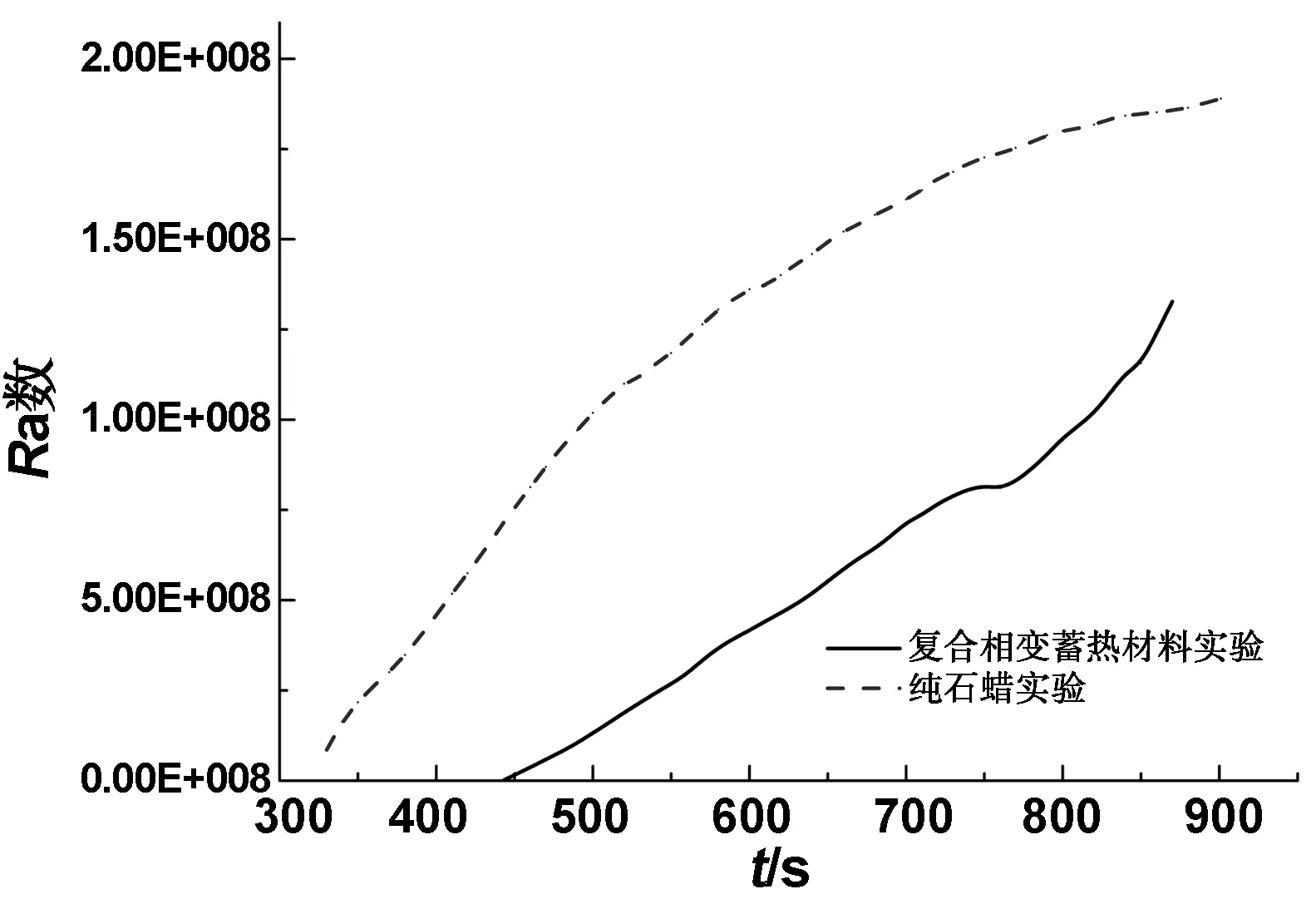
如图10所示，实验装置的对称剖面为矩形腔体，底部填充泡沫金属，内部充满相变材料。底部与左侧为热流边界。泡沫金属孔径小，故内部的自然对流可以忽略。Tm为相变材料的相变温度，Th为加热面温度，Tc为冷源温度。对于泡沫金属实验，因为泡沫铜具有高导热率，所以认为泡沫金属温度为壁面温度，即Th由监测点1测得；对于纯石蜡实验，Th为壁面温度，由实验测得。熔化时Tc和Th满足不等式Tc

图10 固液界面示意图Fig 10 Schematic diagram of solid-liquid interface

图11所示为纯石蜡与复合相变蓄热材料实验瑞利数对比与理论计算值对比。从图中可以看出，纯石蜡实验的瑞利数更大，因此其自然对流更加强烈。随着熔化过程的进行，两者瑞利数之差呈先增大后减小的趋势，在t=650 s时，两者之差最大为9.4×107。文献[18]采用理论N-S方程对三维方腔内自然对流从过渡状态到湍流状态的转变进行了数值研究，提出当瑞利数达到108时，将会使得层流向湍流状态转变。因此，当t=497 s和t=814 s时，纯石蜡实验和复合相变蓄热材料实验分别向湍流状态转变，过渡状态时长分别占熔化过程总时长的44.8%和6.4%。泡沫金属的加入，减弱了石蜡在熔化过程中的自然对流强度，但增强了其底部导热，总体上呈强化效果，强化导热可以有效提高石蜡在相变过程中的蓄/释热速率，进而提高蓄热装置热特性。

图11 纯石蜡与复合相变蓄热材料实验的自然对流对比曲线Fig 11 Comparison curves of natural convection between pure paraffin and composite PCMs

4 结 论

本文通过对复合相变蓄热材料熔化过程进行实验和模拟研究，分析了石蜡-泡沫金属铜复合相变蓄热材料强化传热机理，并进一步研究了泡沫金属铜对相变材料导热性能及对流强度的影响，结果表明：

(1)泡沫金属铜强化了复合相变蓄热材料的导热性能。纯石蜡完全熔化需901 s，复合相变蓄热材料的熔化时间为870 s，较之缩短了3.44%。与纯石蜡熔化过程相比，复合相变材料底部温度升高更快，终温升高15K，且内部温度分布趋于一致，上下部温差为16 K，较纯石蜡减少48.39%。

(2)泡沫金属的加入减小了复合相变材料的瑞利数，纯石蜡和复合相变蓄热材料的瑞利数之差呈先增大后减小的趋势，t=650 s时两者之差最大为9.4×107。泡沫金属减弱了石蜡在熔化过程的自然对流强度，但强化了底部导热能力，缩短了整体熔化时间。过渡状态时长分别占熔化过程总时长的44.8%和6.4%。

(3)实验验证了模拟结果，纯石蜡与复合相变材料模型熔化时间分别快于实验结果19和28 s。RMSE均方根误差分别为0.0223和0.0179。

通过复合相变蓄热材料相变过程的研究，可以进一步了解泡沫金属铜对相变材料导热性能及对流强度的影响，为热能储存装置的设计提供参考。