Li2MSiO4(M = Mn,Fe,Co)力学性能对电化学特性的影响 *
郑寿红,李 伟,姜茗浩,闫小童,侯育花,陶小马
(1. 南昌航空大学 材料科学与工程学院,南昌 330063; 2. 广西大学 物理科学与工程技术学院,广西 南宁 530004)
0 引 言
能源作为人类生产生活的基石与保障,是社会繁荣与发展的重要推动力。然而随着人口数量、能源消耗的增加以及化石燃料的枯竭和生存环境的日益恶化,迫使人们不断发展新型能源材料及储能材料[1]。锂离子电池因具备较高的工作电压、能量密度、输出功率以及对环境友好等特点[2]而受到广泛关注。自从Sony公司上个世纪九十年代,首次将LiCoO2作为正极材料的锂离子电池成功商业化之后,锂离子电池进入了飞速发展的时期。紧接着以尖晶石型LiMn2O4、橄榄石型LiFePO4和硅酸盐类Li2FeSiO4等作为正极材料的锂离子电池也相继被发明与应用[3-4]。其中硅酸盐类正极材料Li2MSiO4(M = Mn, Fe, Co)因为具有高放电比容量(理论比容量高达330 mAh/g)[5]、主体结构稳定性(具有稳定的Si-O共价键)[6]等特点而受到广泛关注。
然而,硅酸盐类正极材料Li2MSiO4(M = Mn,Fe,Co)在电化学特性和循环稳定性等方面的不足限制了其进一步发展。Dominko等[5]采用溶液-凝胶法合成了Li2MnSiO4正极材料,其最大的特点就是具备高的理论放电比容量(高达330 mAh/g),但是较差的导电特性和循环稳定性限制了其发展。研究表明Li2MnSiO4具有较差的循环稳定性主要归因于脱锂过程中非晶化现象的发生[7]以及Mn3+/4+离子的Jahn-Teller效应[8]。对于Li2FeSiO4正极材料,其最大特点是具备较好的循环稳定性,但是其实际放电比容量在首次充放电循环时只有165 mAh/g,并最终稳定在140 mAh/g[9],这与理论放电比容量330 mAh/g相差较大,较大程度上限制了Li2FeSiO4成为高性能锂离子电池正极材料。此外,Li2CoSiO4正极材料因其较高的充放电平台导致现有的电解液无法满足其使用要求以及较差的循环特性也使得其应用受到限制[3]。
研究者们从实验和理论的角度出发,对硅酸盐类正极材料Li2MSiO4(M = Mn,Fe,Co)的性能改善和机理研究均做了大量工作[10-13],由于实验条件的影响,对Li2MSiO4(M = Mn,Fe,Co)的力学性能研究是鲜有报道,而力学性能的优异与否将对正极材料的各项性能产生非常重要的影响,因此对正极材料各项力学性能参数的研究是非常有必要的。本文运用基于密度泛函理论框架下的第一性原理计算方法,尝试计算了硅酸盐正极材料Li2MSiO4(M = Mn, Fe, Co)的弹性常数Cij、体积模量B、剪切模量G、泊松比ν、杨氏模量E以及德拜温度θD等参数,在一定程度上对Li2MSiO4(M = Mn,Fe,Co)体系力学性能对其电化学特性的影响进行了预测与分析。
1 计算方法与模型
1.1 计算方法
本文采用VASP(Vienna Ab initio Simulation Package)软件包作为主要的计算软件[14],并运用以密度泛函理论为基础的投影缀加波法projector augmented wave(PAW)进行计算[15]。截断能取值经过测试选取500 eV,用Monkhorst-Pack方法生成9×9×9的布里渊区K点网格。交换关联近似则选取广义梯度近似Generalized Gradient Approximation(GGA)条件下的Perdew-Burke-Ernzerhof(PBE)泛函[16]。自洽过程中电子的能量收敛标准为1.0×10-6eV,且原子间的相互作用力不大于0.01 eV/0.1 nm。此外,因为过渡族金属M(M = Mn,Fe,Co)3d轨道电子间的强关联相互作用,本文为提高计算的准确性,加入了Hubbard参数Ueff进行修正[17]。在GGA+U条件下,经过测试不同Ueff值条件下理论平均脱嵌电压与实际放电平台之间的关系,过渡族金属Mn、Fe和Co的Ueff值分别选取4.5、4和5.5 eV,其具体测试结果如图1所示。

图1 不同Ueff值条件下理论平均脱嵌电压与实际放电平台之间的关系Fig 1 The relationship between theoretical averagedeintercalation voltages and actual discharge platforms under different Ueff values
1.2 计算模型
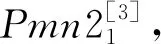
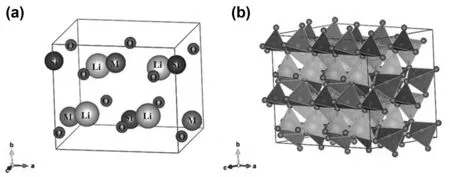
图2 (a)Li2MSiO4(M = Mn,Fe,Co)晶胞结构;(b)相应的超胞结构Fig 2 Crystal cell structure of Li2MSiO4 (M = Mn, Fe, Co) and the corresponding supercell
2 结果与讨论
2.1 结构分析
本文在GGA+U的计算条件下,计算得出了Li2MSiO4(M = Mn,Fe,Co)体系的具体晶胞参数,如表1所示。计算所获得的晶胞参数与实验值符合较好,表明本文所采用的GGA+U算法符合该体系。此外,通过分析比较计算理论值和实验值可知, Li2MnSiO4拥有最大的晶胞体积,其次分别为Li2FeSiO4与Li2CoSiO4,这种晶胞体积的变化趋势一定程度上取决于M(M = Mn,Fe,Co)的原子半径大小。

表1 Li2MSiO4(M = Mn,Fe,Co)的晶胞参数
2.2 理论平均放电电压分析
通过计算脱锂前后正极材料反应物与生成物的基态能量差值,便可得出相应的理论平均脱嵌电压[10],其计算公式如下所示:
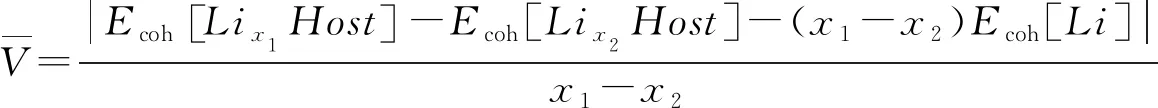
(1)
式中Ecoh[Lix1Host]与Ecoh[Lix2Host]分别代表脱锂前后体系的晶胞能量,Ecoh[Li]表示BCC结构Li单质的晶胞能量,x1与x2分别表示脱锂前后晶胞中Li+的浓度。计算得出Li2MSiO4(M = Mn,Fe,Co)的理论平均脱嵌电压如图3所示。
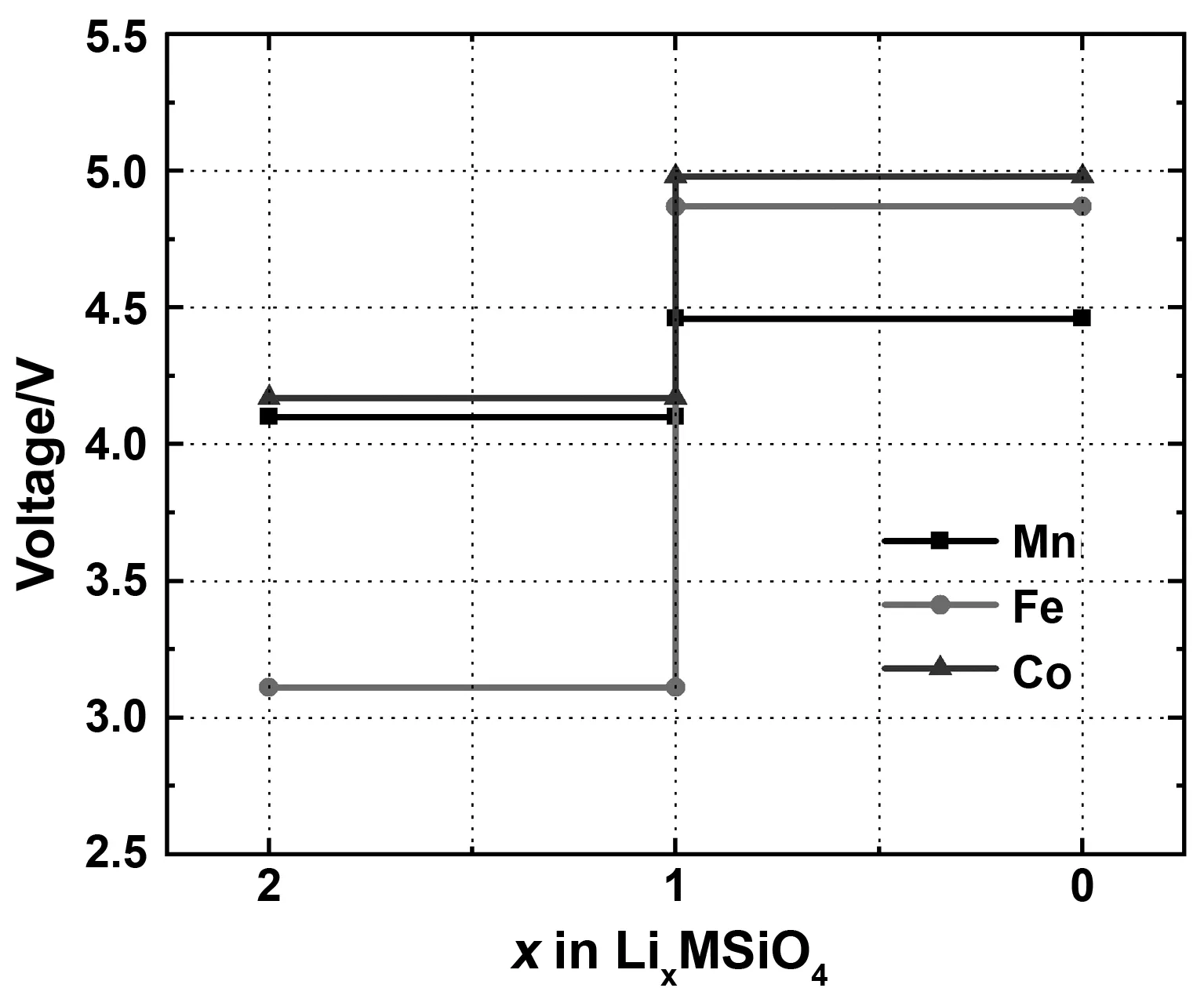
图3 Li2MSiO4(M = Mn,Fe,Co)的理论平均脱嵌电压Fig 3 Average deintercalation voltages of Li2MSiO4 (R = Mn, Fe, Co)
由图3可知,Li2MnSiO4,Li2FeSiO4与Li2CoSiO4单位公式内第一个Li+脱嵌时的理论平均电压分别为4.1,3.11与4.17 V,与实验结果一致[7,9,18]。此外,分析图3中数据可知,对于Li2MnSiO4体系,与Li2MSiO4(M = Fe,Co)相比,其一次脱锂与二次脱锂之间的理论平均脱嵌电压差值最小为0.36 V。对于Li2FeSiO4体系,与Li2MSiO4(M = Mn,Co)相比,虽然其一次脱锂时的理论平均电压最低,但是其一次脱锂与二次脱锂之间的理论平均脱嵌电压差值却最高为1.76 V,这主要归因于Li2FeSiO4一次脱锂时,Fe离子将由+2价氧化至+3价,相应的其3d轨道的电子排布也由3d6变为更为稳定的3d5半满结构,这一过程仅需要较少的能量。而当体系进行二次脱锂时,Fe离子将由+3价氧化至+4价,其3d轨道的电子排布将由稳定的半满结构排布3d5向不稳定的3d4排布转变,这一过程将需要较高的能量,因此对于Li2FeSiO4正极材料来说,使其完全脱锂是十分困难的[19]。而对于Li2CoSiO4体系,与Li2MSiO4(M = Mn,Fe)相比,在整个脱锂过程中其理论平均脱嵌电压均为最高值,其原因之一是Co2+对其3d轨道电子的强烈束缚作用[20]。
此外,为了更好的厘清Li2MSiO4(M = Mn,Fe,Co)的电化学特性,本文还计算了Li2MSiO4(M = Mn,Fe,Co)的理论放电比容量及其能量密度,其具体的计算数值如表2所示。

表2 Li2MSiO4(M = Mn,Fe,Co)的理论放电比容量及能量密度
分析表2中数据可知,Li2MSiO4(M = Mn,Fe,Co)的理论放电比容量依次降低,其主要原因是Mn、Fe和Co的相对原子质量是依次递增的进而使得体系的理论放电比容量呈现出不断下降的趋势。此外,分析表2中的能量密度参数可知,Li2FeSiO4表现出最低的能量密度,而Li2CoSiO4却表现出最高的能量密度,这主要是因为正极材料的能量密度主要由体系的理论平均放电平台与理论放电比容量共同决定,因此Li2FeSiO4(Li2CoSiO4)所表现出最低(最高)的理论平均脱嵌电压,对体系的能量密度产生了影响。
2.3 力学性能分析
为了厘清Li2MSiO4(M = Mn,Fe,Co)体系的力学性能,本文采用应力-应变法[3],对Li2MSiO4(M = Mn,Fe,Co)体系的弹性常数矩阵[Cij]进行了计算,其具体数值如表3至表5所示。
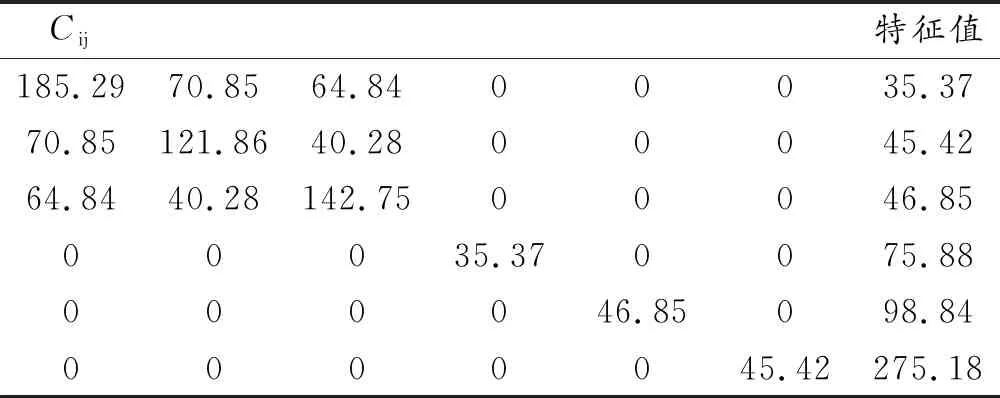
表3 Li2MnSiO4的弹性常数

表4 Li2FeSiO4的弹性常数
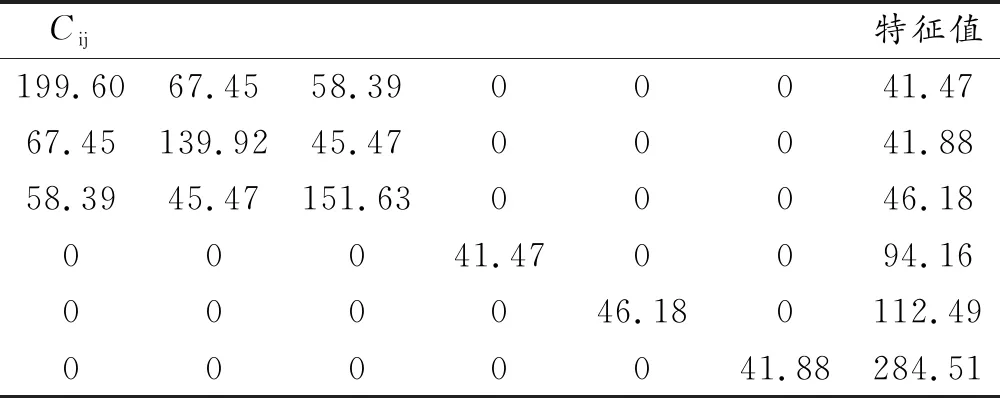
表5 Li2CoSiO4的弹性常数
由表3至表5中的特征值可知,Li2MSiO4(M = Mn,Fe,Co)体系的特征值均为正,表明Li2MSiO4(M = Mn,Fe,Co)体系的晶体结构是稳定存在的[21]。根据表3至表5中的弹性常数矩阵[Cij],本文采用Voigt-Reuss-Hill近似的方法[22-24],运用公式(2)至(14),对Li2MSiO4(M = Mn,Fe,Co)体系的体积模量B、剪切模量G、模量比B/G、泊松比ν、杨氏模量E和德拜温度θD等进行详细计算。具体的力学性能参数如表6所示。

表6 Li2MSiO4(M = Mn,Fe,Co)的体积模量B、剪切模量G、模量比B/G、泊松比ν、杨氏模量E和德拜温度θD
9BV=(c11+c22+c33)+2(c12+c23+c31)
(2)
15GV=(c11+c22+c33)-(c12+c23+c31)+3(c44+c55+c66)
(3)
BR=1/[(s11+s22+s33)+2(s12+s23+s31)]
(4)
GR=15/[4(s11+s22+s33)-4(s12+s23+s31)+3(s44+s55+s66)
(5)
[S]=[C]*/│C│
(6)
公式(2)至(6)中的BV、GV是根据Voigt理论获得,而BR与GR则是根据Reuss理论获得。Hill认为根据Voigt与Reuss理论计算获得的结果可以看做体系模量的上下限,所以其提出用算术平均值来表示体系的体积模量B与剪切模量G,具体公式如(7)和(8)所示。公式(6)中的[S]为相应体系的柔顺系数,其具体数值是对相应体系的弹性常数矩阵[Cij]取逆来获得。
B=(BV+BR)/2
(7)
G=(GV+GR)/2
(8)
公式(9)与(10)是计算体系泊松比ν与杨氏模量E的具体公式。
ν=(3B-2G)/[2(3B+G)]
(9)
E=9BG/(3B+G)
(10)
公式(11)为计算体系德拜温度θD的具体公式. 公式(11)至(14)中的ħ为普朗克常数,kB为玻尔兹曼常数,vm为平均声速,vt为横向声速,vl为纵向声速,ρ为体系的密度。
θD=(ћ/kB)(3n/4πV)1/3νm
(11)
(12)
νt=(G/ρ)1/2
(13)
νl=[(3B+4G)/3ρ]1/2
(14)
模量比B/G的引入是为了对材料的延展性进行评估。其数值高(低)值与体系的韧性(脆性)有关,评判材料韧性或脆性的经验标准数值为1.75[23]。由表6可知,Li2MSiO4(M = Mn,Fe,Co)的B/G值分别为1.97,2.19和1.94,表明Li2MSiO4(M = Mn,Fe,Co)体系均表现出良好的韧性,特别是Li2FeSiO4的B/G值最高,表现出最好的延展特性。类似的,泊松比ν也是判断材料延展性的重要指标,其评判标准约为0.3[24],根据计算所得的泊松比ν可知,Li2MSiO4(M = Mn,Fe,Co)体系也均表现出良好的力学性能,与模量比B/G的比较结果相似,Li2FeSiO4也表现出最优的延展性特性。通过分析模量比B/G和泊松比ν可知,在Li2MSiO4(M = Mn,Fe,Co)体系中Li2FeSiO4具有最佳的力学性能,这与Li2FeSiO4具备良好循环稳定性的实验报道是相符的[9]。此外,杨氏模量E的大小和德拜温度θD的高低,则在一定程度上体现着体系原子之间相互作用力的大小。理论上杨氏模量E和德拜温度θD数值越小,其原子之间的相互作用力就越小,这对正极材料来说,将有助于Li+的脱离[23]。由表6可知,Li2FeSiO4与Li2CoSiO4分别具备最小(最大)的杨氏模量E和德拜温度θD,这与文献中报道的Li2FeSiO4具备最低的放电平台,Li2CoSiO4具备最高的放电平台且Li+难以脱离的报道是相符的[3,25]。
3 结 论
本文运用第一性原理的计算方法对Li2MSiO4(M = Mn,Fe,Co)正极材料的力学性能进行了系统的研究。研究发现,对于Li2MSiO4(M = Mn,Fe,Co)体系,其模量比B/G与泊松比ν均高于和接近其韧脆转变临界值,表明Li2MSiO4(M = Mn,Fe,Co)正极材料均表现出较好的延展特性,其中Li2FeSiO4正极材料的力学性能最为优异。此外通过对体系的杨氏模量E与德拜温度θD的研究可知,Li2CoSiO4电极材料具备最高的杨氏模量E和德拜温度θD,表明其具有较强的原子间作用力,不利于Li+的有效脱离,与已有的实验结果符合较好。

