三坐标测量机接触模型构建及数值算法研究
薛 秦,朱僖禧
(中国矿业大学徐海学院 信息与电气工程系 ,江苏 徐州 221008)
0 引言
在精密制造领域中,球类零件的应用日趋广泛,对球面的精度要求也越来越严格。球面的形状误差,其精度高低对球类零件的质量、工作性能和使用寿命有很重要的影响。在精密测试领域,计算机辅助测试技术不仅能完成尺寸、曲线、曲面的精密测量,还能进行形位误差的精确评定[1-3]。微纳米坐标测量机(CMMs)作为一种测量仪器,它的出现标志着计量仪器从传统的手动测量向现代化的自动测试技术过渡的一个里程碑。通过对三坐标测量机探头球面中心的坐标测量,将其转换为被测表面各点的坐标。这个过程通常称为测量探头半径的补偿[4-6]。在实际测量中,曲面在形状和位置上的偏差量总是与计算机辅助设计测量模型不同。对于探测球头上的点的坐标,它是在一定误差下确定的[7-8]。复杂曲面确定点的坐标与被测表面的曲率以及探头球体的半径有关,被测表面曲率和探头球体的半径越大,确定表面点的坐标时产生的误差就越大[9-11]。
在实际测量轴承、凸轮、机床、机身和涡轮叶片等零件的复杂表面时,通常需要在探测球头球体形状等方面考虑以提高其精度[12]。针对目前CMM在复杂曲面测量中缺乏一个完整的数学体系,提出了一种新的球头与零件表面接触点的数学模型和数值算法。即使在球面上使用了大量的点,也具有良好的收敛性。实验在测量圆环形标称表面的滚珠轴承内圈与凸轮轮廓时,成功地测试了球形探针半径补偿形状误差的方法,并且得到实际的凸轮轮廓线。
1 复杂曲面与球体半径补偿
以前能够实现三维补偿确定曲面法向经常用的是微平面法。为了确定被测曲面的法向,如图1所示,可以在Q点附近测若干个点,例如测Q1、Q2、Q3,三个点(也可以取多个点),然后通过Q1、Q2、Q3三点作一个平面,这一微小平面的法线即近似为曲面的法线。为了确定Q点的法线方向,通常采用方形网格,如图2所示。但不是简单地在Q点附近再去测4个点,而是利用与它相邻近的4个网格点Q1、Q2、Q3、Q4,然后用最小二乘法确定它的最佳拟合平面及其法线方向。值得注意的是,在实际测量中,直接得到的并不是测量点Q与Q1、Q2、Q3、Q4的坐标,而是测量Q点和Qi点时测端球心位置Q及Qi的坐标,必须根据这些拟合平面的法向进行测头半径补偿,才能得到Q和Qi各点坐标值。
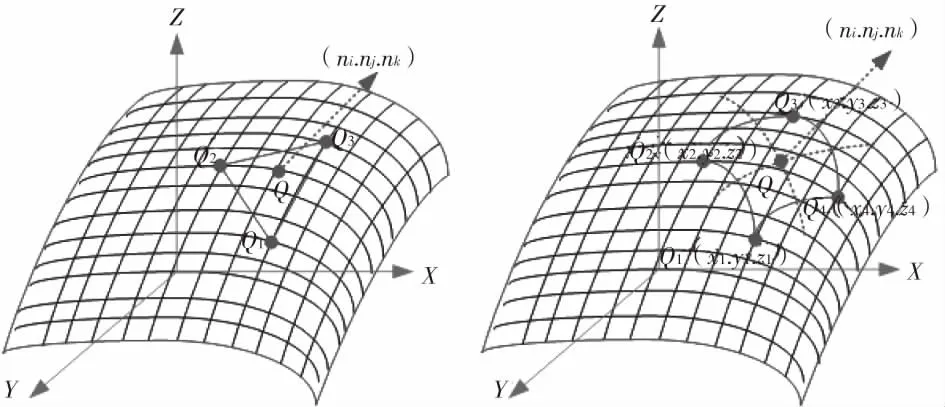
图1 微平面法三维补偿 图2 微平面法求曲面法向
在计算复杂曲面与球体之间的接触点坐标时,通常因为名义曲面和实际曲面两者的法线不一致而产生误差。这跟曲面的形状和控制点的错误排列有很大的关系,而这些因素在现阶段无法确定。因此,现在的很多研究人员倾向于借助于各种算法来优化法线的位置,从而使误差最小化。接触点坐标的准确度与探头球体的形状和尺寸密切相关。大量的测量实验表明球内误差占总测量误差的10.4%以上,这对于复杂曲面的相关研究工作及其不利[13-14]。因此针对探测球头形状偏差,本文提出了一种新的方法来测量复杂曲面。在该方法中,对测得球面上的点进行双三角多项式逼近并建立其三维模型。图3则为半径补偿的测头和零件的理想接触示意图。
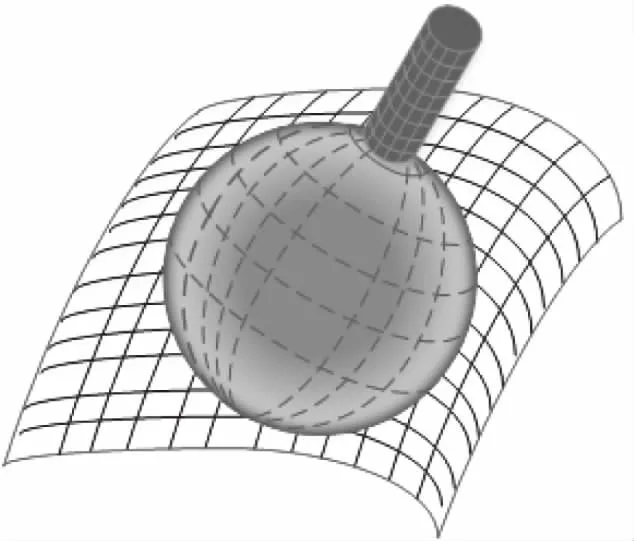
图3 测头和零件的理想表面
本文提出的方法主要针对探测球头的形状偏差,需要建立一个新的数学模型。算法使用球体表面任何点的法线通过其中心。因此,复杂曲面与探测球体接触点的计算是通过一种数值算法来实现。利用球面上的点在法向上与标称表面的距离最小。因此探测球体面向被测表面部分上的所有点形成一个循环,然后在与法向相交的条件下,在名义面上均有一个对应点;最后从找到的所有距离值中选择一个最小距离,根据最小距离值δi,可以认为球体与复杂曲面的接触点位置即对应于找到的最小距离的方向。
2 三坐标测量曲面模型构建
使用三个笛卡尔坐标系(图4)进行坐标测量。其中包括:(1)坐标测量机固定系统(X0,Y0,O0,Z0);(2)固定件系统(X1,Y1,O1,Z1);(3)移动探针系统(X2,Y2,O2,Z2)。一般情况对于三个坐标系而言,它们的相互位置是已知的。通过使用CMM软件来完成一个坐标系到另一个坐标系的转换。
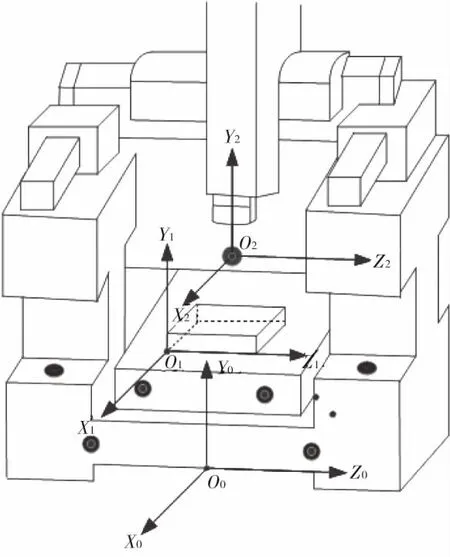
图4 CMM测量坐标系模型
计算的初始数据:1)坐标x1、y1、z1和法线方向n1X、n1Y、n1Z的零件标称表面;2)中心坐标为x20,y20,z20和表面坐标为x2i,y2i,z2i的球体。
接触点处标称表面的法向参数方程为:
(1)
其中t是标准参数。
球体的参数方程可以表示为:
(2)
其中,θ,φ是球体在经纬度上的角度;ri是球体上第i个点的半径。具体示意图如图5所示。球面点的半径ri可以以数组的形式给出(θ,φ,ri)或通过依赖关系近似:
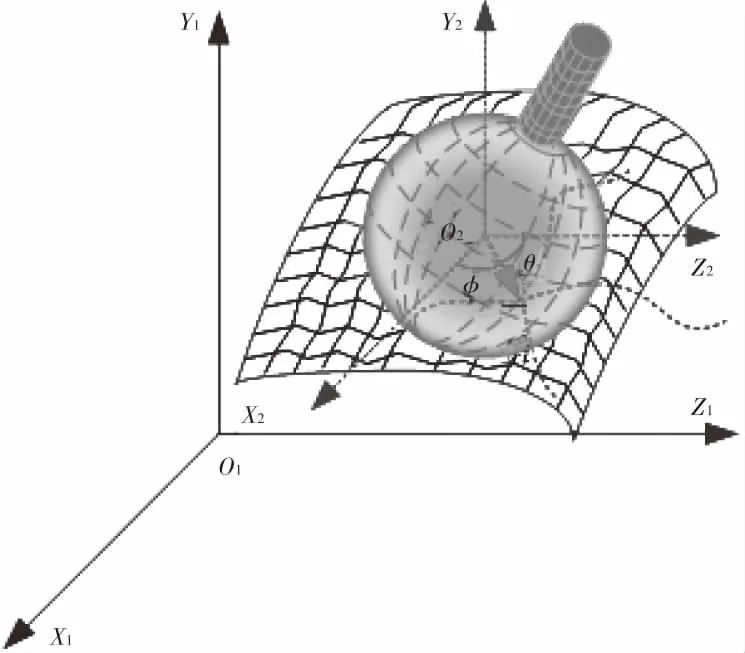
图5 切点计算空间模型
(3)
式中,r0是球体的平均半径,k、m是经纬度中的谐波数,ak、am、φk、θm是谐波的振幅和初始相位。
通过将方程组(1)和(2)的右侧相等,可得出:
(4)
由式(4)可以得到法向与名义面和球面相交点的坐标。如式(5):
(5)
在坐标轴上的投影中,法向方程的形式为(式中,u、φ是零件标称表面的曲线参数):
(6)
结合公式(5)和(6)可得出:
(7)
对(7)式用数值方法进行求解。将计算出来的参数θ和φ的值带入(2)式中,计算球面上点的笛卡尔坐标。假设用实线表示实际的复杂曲面,虚线则表示标称表面。分别计算从球体上的第i个接触点到零件标称表面的距离δi。从得到的δi值中,选择与实际接触点对应的最小值。
上面提出的数值方法收敛的条件可以归纳为:1)被测量表面不存在奇异点;2)被测曲面曲率小于测球曲率。在实际测量实验中,可以对测头进行正确选择以达到这些条件。本文所提出算法的优点明确,对于复杂曲面测量测点位置分布不均匀的问题,测头探测的精度以及收敛性不受其影响。
3 实验验证
通过实验测量凸轮轮廓以及测量圆环形标称表面的滚珠轴承内圈,成功地测试了球形探针半径补偿形状误差的方法。坐标测量机作为一台高精密的测量系统,它对于环境因素(空气、温度、湿度)要求非常高。因此本文中CMM安放在精密恒温箱内,高精密恒温箱本身放置在一间温度变化在20 ℃±0.05 ℃、相对湿度值(RH)为50%的恒温室内。这样做的目的是尽量减小外界因素对CMM测长系统的影响,以便提高微纳米三坐标测量机的稳定性情况。坐标测量机的体积误差为1.76+L/332 μm,探头长度为58 mm,探头球体直径为1.89 mm。CMM将测量结果保存为探头球体中心点的坐标。根据CMM软件中的标准算法和自行开发的MATLAB算法对数据进行处理。
凸轮轮廓经三坐标测量机测量后,以文本文件格式输出,直接读取测量结果,可以根据需要设定直角坐标或极坐标输出。表1以及表2为得到的红宝石测球中心点的坐标及测头经过补偿后的被测轮廓点的坐标,以直角坐标的形式显示,补偿后的点形成的轮廓线即为凸轮的实际廓线。
从表1以及表2可以看出,补偿后实际轮廓线点的坐标更加准确。将上述数据读入相关工程软件,即可快速得到凸轮的实际表面廓线。然后根据软件的功能,可以根据需要与理论廓线进行比较,或做出所需的零件三维实体模型,快速直观地了解产品的形状,为设计制造提供可靠的理论依据。如图6所示的是在软件中表示的凸轮轮廓线,外侧的曲线为测量形成的测头球心轨迹线,内侧的曲线为测头直径经过补偿以后的凸轮实际轮廓线。如果凸轮为内凹型,则应向外侧补偿测头半径,以得到实际的凸轮轮廓线。
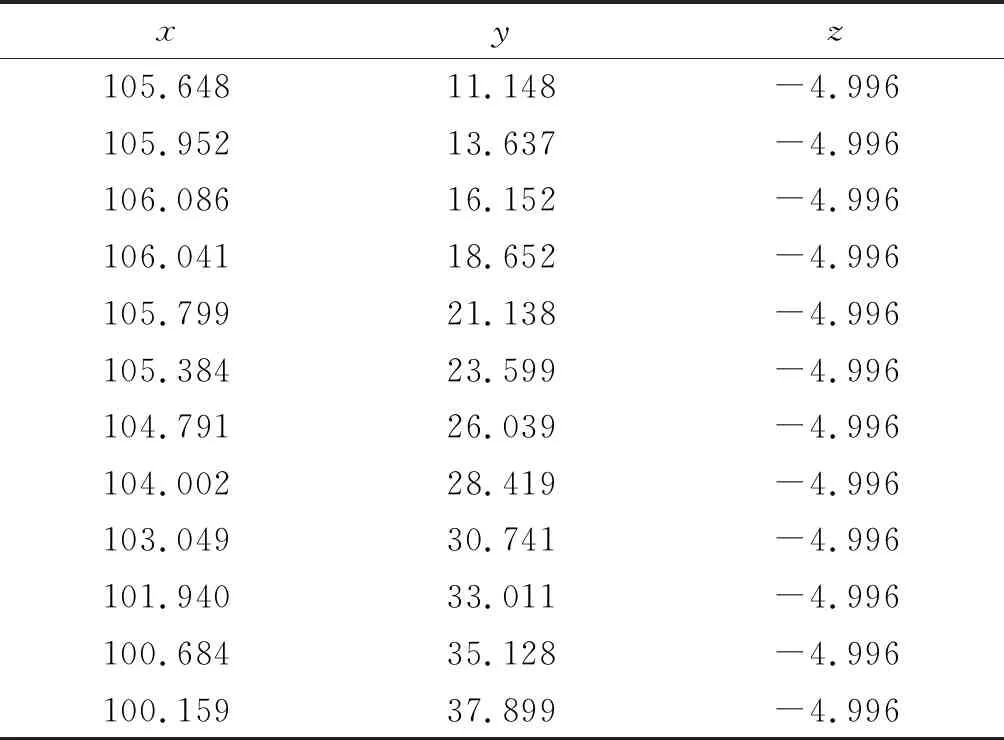
表1 测头中心点坐标(单位:μm)

表2 补偿后实际廓线点的坐标(单位:μm)
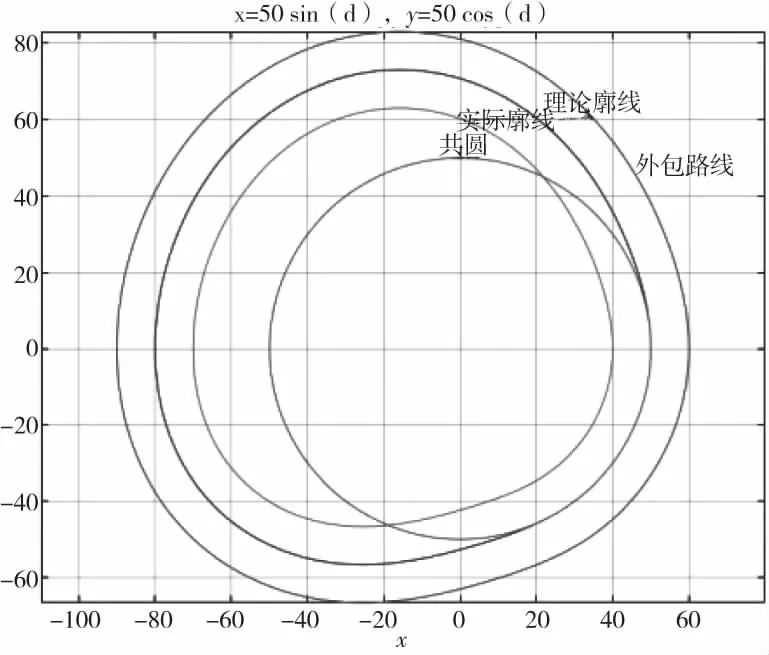
图6 凸轮轮廓线
圆环体经三坐标测量机测量后,根据标准算法与本文提出算法所测得的形状误差数据拟合图如图7和图8所示。
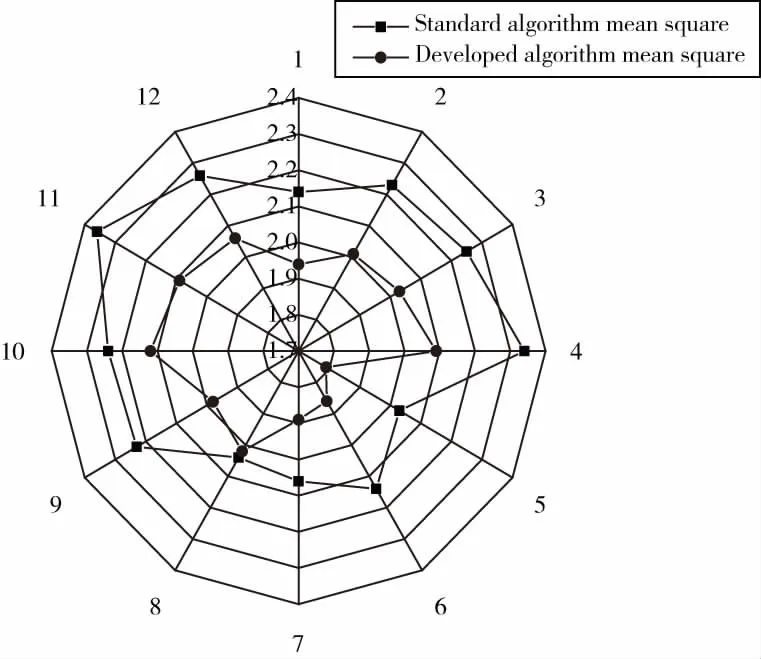
图7 圆环体被测量表面形状误差均方差对比
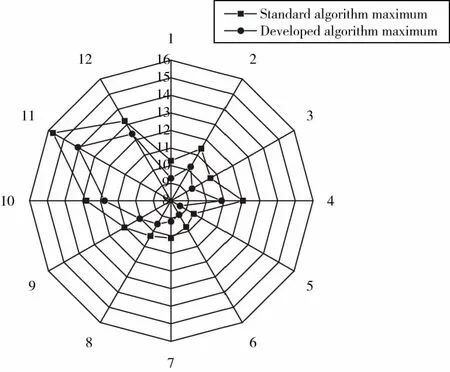
图8 圆环体被测量表面形状误差最大值对比
由图7和图8中的数据分析表明,本文所提出的算法在考虑了探头球体形状的情况下,所得出的测量结果误差小。在圆环体的12个被测截面中,标准算法的形状误差在9.48~15.71 μm之间,改进算法的形状误差在8.59~14.08 μm之间,采用新的数学模型和数据处理算法,使测量误差平均降低了11.88%。
4 结果分析
本文建立了一种新的球头与零件表面接触点的数学模型和数值算法。研究过程中充分考虑球面探针的形状,可以减小复杂曲面的测量误差。该算法的核心思想是球面上的点阵列在法向上与标称表面的距离最小。实验测量凸轮轮廓以及测量圆环形标称表面的滚珠轴承内圈,成功地模拟出凸轮轮廓线形状。通过对滚动轴承内圈环面测量算法的验证,表明该算法可以将形状误差降低11.88%。实验成功地测试了球形探针半径补偿形状误差的方法。因此,所建立的数学模型将有助于在CMMs上测量复杂而精密的曲面,进一步阐明了测头补偿技术的核心问题与关键技术,具有较强的实用性,将对曲线、曲面的测量具有重要的意义。

