基于推断模型(IM)的配对试验优势比检验方法
王枝宁
(韩山师范学院 数学与统计学院,广东 潮州 521041)
随着经济社会的发展,新的生物制药不断推陈出新.一般来说,新药品必须具有一些目前广为使用的药品(或称为“标准药品”)所不具有的新的优点.本文聚焦生物医学统计研究中关于两种药物试剂的非劣效性的评估.对于配对试验而言,它常常包含新旧两种药物的有效率的比较,这主要来源于医学上的前瞻性研究和回顾性研究中.如果新药具有较大优势,如无副作用、易于生产或者价格低廉,那么我们常常关心这些新药是否与目前广为使用的标准药品具有一样的效果,或者不差于现有的标准药品.对于前瞻性研究和回顾性研究,人们常常用优势比来评估两种新旧药品在统计学上的差异.在已有的统计学文献中,这一问题受到了许多统计学者的重视[1-4].
为方便起见,本文仅考虑前瞻性研究的情形.一个医学背景就是对N个病人采用标准药物来治疗某种疾病,与其配对的另外N个病人(这N个病人与标准药物对应的病人有相同的病情、年龄、身高、职业等)采用新药来治疗.基于上述的背景,可构建统计模型如下:假设有N对配对的随机试验,记为(Y1j,Y2j),j=1,2,…,N,其中对于第j对而言,Y1j和Y2j分别为二项分布随机变量,用1 表示“有效”,2代表“无效”.表1给出了配对试验后的四种结果以及相应的概率,其中a,b,c和d分别表示观测结果为(1,1),(1,2),(2,1)和(2,2)所对应的配对数,p11,p12,p21和p22为上述四种观测结果所对应的概率.易知四元随机变量(a,b,c,d)服从于p11+p12+p21+p22=1的三项分布.

表1 配对试验中观测值和概率的2×2 列联表
为了检验新药是否不差于标准药物,需要作如下非劣性假设检验:

其中δ=p12/p21,δ0(0<δ0<1)是事先给定的、临床上有意义的非劣边界值.
Liu et al.[5]提出了作假设检验(1)的两种检验方法.一种是Delta检验,其检验统计量为:

另一种是Score检验,其检验统计量为:

在原假设δ=δ0前提下,上述两个检验统计量都是服从渐进标准正态分布.由于其渐进性,其检验的决策准则可能是不精确的,并未像他们所声称的都能够控制住第一类错误率,尤其在小样本的情形下.为克服上述检验方法的缺点,Jin[6]构建了一种基于推断模型(Inferential Model)的检验方法(以下简称IM检验).所谓推断模型,是由Martin和Liu[7]提出的一种合适的无先验概率推断方法,其在医学统计中具有重要的应用.模拟研究显示IM检验对于给定显著性水平,都能够控制住第一类错误率,但是这种方法显得过于保守,以致跟Delta检验和Score检验相比,其统计功效不高.
本文重新考察了IM检验,并基于推断模型构造了一种新的合适且有效的检验方法称为随机化推断模型检验,即RIM(Randomized Inferential Model)检验.这种方法不仅对于给定的显著性水平都能够控制住第一类错误率,并且其统计功效也不比Delta检验、Score检验和IM检验差.
1 方法论

1.1 IM检验
Jin[6]所提出的IM检验包括如下三个步骤:
A-步(Association)对于上述分布模型而言,其联结模型为

其中Fn,θ(⋅)表示二项分布B(n,θ)的累积分布函数,v为服从(0,1)均匀分布的辅助变量.
P-步(Prediction)对于给定的断言A={θ:θ≤θ0},关于v的最优随机预测集是

C-步(Combination)将Θb(v)和S组合起来就得到
因此关于断言A的合理性函数(Plausibility function)为
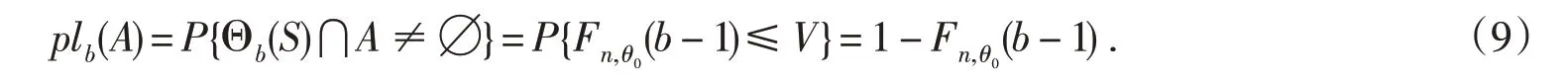
基于上述合理性函数,对于断言A来说,其检验准则为:若plb(A)≤α,则拒绝H0.
根据Martin 和Liu[7]的理论,易知上述检验准则对于给定显著性水平都能够控制住第一类错误率,模拟研究也证实了这一点[6].然而,这种方法太过于保守,导致其检验功效比频率学派的方法低.因此,本文将IM检验拓展为基于随机化合理性函数的RIM检验.
1.2 RIM检验
注意到(6)式中联结模型Θb(v)是关于θ的不等式(其本质上是由抽样模型的离散性决定的),尽管(7)式是关于v的最优随机预测集,但是组合后的Θb(S)却不是最优的.由此导致关于参数θ的推断可能不是有效的.基于此,将上述关于θ的不等式联结模型修正为一个精确的等式联结模型,以此提高组合步中Θb(S)关于参数θ的有效推断.事实上,观察(6)式可知,由于辅助变量v落在区间[Fn,θ(b-1),Fn,θ(b)),因此存在一个权数w∈(0,1),使得v=wFn,θ(b-1)+(1-w)Fn,θ(b).
进一步,通过研究发现,当权数w 在均匀分布(0,1) 中随机取值时,随机变量wFn,θ(b-1)+(1-w)Fn,θ(b)确实是服从(0,1)上的均匀分布.
定理1 给定b+c=n,假设b服从二项分布B(n,θ).令w服从(0,1)上的均匀分布.b与w之间是相互独立的,则有
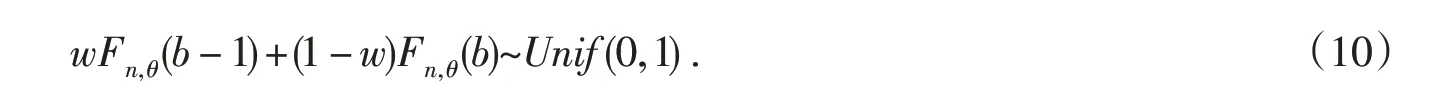
证明对于任意给定的α∈(0,1),存在一个k=0,1,2,…,n,使得Fn,θ(k-1)≤α 由此可知wFn,θ(b-1)+(1-w)Fn,θ(b)~Unif(0,1).证毕. 以下均假设w服从(0,1)上的均匀分布,利用定理1将上述IM模型构造的三步法重新改写如下: A'-步(Association)记H(θ)≡wFn,θ(b-1)+(1-w)Fn,θ(b).易见对于给定b,c 和w,Fn,θ(b-1),Fn,θ(b)和H(θ)都是关于θ的严格单调递减函数.令H-1(⋅)为H(⋅)的反函数,则新的随机联结模型表示如下: P-步(Prediction)根据Martin和Liu[7]定理4,仍然使用上述(7)式的最优随机预测集来预测辅助变量v. 则相应地关于断言A的合理性函数为 由于w 是取自(0,1)上的均匀分布的一个随机数,故式(13)是一个“随机化”(randomized)的合理性函数,简称为“随机化合理性函数(randomized plausibility function)”.基于式(13),可以定义如下的准则. 定义1 (RIM检验)基于表1的配对试验统计模型,对于给定数据b和c,先在区间[0,1]中随机选择一个权数w.对于给定显著性水平α,若 则拒绝H0.称基于此随机化合理性函数的统计模型为随机化推断模型(Randomized Inferential Model,以下简记为RIM),基于该模型的检验准则称为RIM检验. 定理2 RIM检验不仅是合适(Valid)的,并且是有效(efficient)的.即对任意给定α∈(0,1), 证明事实上,只需证明,对于给定的α∈(0,1), 这等价于证明当θ=θ0, 或者 成立.这实际上已由定理1保证了.证毕. 本文采用4个蒙特卡洛模拟试验来评估RIM检验在控制第一类错误率和提高统计功效上是否优于Jin[6]提出的IM检验和Liu[5]提出的Delta检验、Score检验. 为考察样本量、标准处理方法有效率的大小、基于原假设和备择假设下优势比的差异对随机试验的影响,本文在设置试验参数时,对于大样本试验而言选取N=100 500,对于小样本而言选取N=20,30;p21按步长0.05从0.20增加到0.30;非劣边界值δ0=0.8,0.9;在研究统计功效时其对应的非劣边界值为δ1=1.25,1.11. 首先,为评估4种检验方法控制第一类错误率的表现,利用计算机R语言随机模拟实验100 000次.由中心极限定理,在给定显著性水平5%下,第一类错误率的95%的置信区间为(0.048 6,0.051 4).表2和表3给出了对于大样本和小样本两种情形下4种检验方法在控制第一类错误率的比较结果.正如表2 和表3 中结果所示,由于Delta 检验和Score 检验的检验统计量都是渐进服从正态分布的,因此,在一些情形下其第一类错误率超出95%的置信上限0.051 4,即使是大样本的情形也是如此.另一方面,对于IM 检验而言,在模拟研究的所有情形下,其第一类错误率均低于95%的置信下限0.048 6,表明它显得过于保守.与上述3种方法对比,RIM检验在所有模拟情形下既不保守也不过于自由,因为其第一类错误率均非常接近给定的显著性水平0.05.这与定理2中RIM检验的有效性证明是一致的.从这个意义上讲,RIM检验在这4种方法中是最优的. 表2 大样本下100 000次模拟试验4种检验第一类错误率的比较 表3 小样本下100 000次模拟试验4种检验第一类错误率的比较 其次,考察4种检验方法的统计功效.类似地用计算机R语言进行100,000次模拟试验,表格4和表格5分别给出了大样本和小样本情形下4种检验方法的功效比较情况.从表格中可以看出,4种方法中,由于IM检验的保守性,其统计功效是最差的;从表4中易知,大样本试验中,在一些情形下RIM检验的功效比Delta 检验和Score 检验高,而在其余的情形中,RIM 检验的功效非常接近Delta 检验和Score检验.总的来说,RIM检验在4种方法的表现中也是最优的. 表4 大样本下100 000次模拟试验四种检验统计功效的比较 本部分将运用RIM检验分析一个实际数据的例子,并与其它3种检验方法作比较.该数据来源于Lachin[8]的一个回顾性配对试验研究.该研究想评估女性服用结合雌激素与子宫内膜癌的发生是否有关系.该实验的数据结构如表6所示. 表6 女性服用结合雌激素与子宫内膜癌的观测数据的2×2 列联表 假设想要证实女性服用结合雌激素,其发生子宫内膜癌的可能性至少是未服用者的2倍,则意味着假设检验(1)式中的δ0=2.容易计算Delta 检验统计量zD=2.279,Score 检验统计量zS=2.378,它们的检验p值分别为0.011和0.009.对于IM检验而言,其合理性函数的值为0.010.上述3种检验方法的p值均小于0.05. 为了运用RIM检验,首先需要先选择一个随机数w~Unif(0,1),然后基于(13)式计算随机化合理性函数.基于R语言程序,例如,取w=0.829,则随机合理性函数的值为0.009.读者可能注意到,在δ0=2 这种情形下,无论随机权重w如何取,其随机化合理性函数的值均小于0.010.综上所述,在5%的显著性水平下,上述4种方法均得出同样的结论,即女性服用结合雌激素,其发生子宫内膜癌的可能性至少是未服用者的2倍. 但是,假设想证实女性服用结合雌激素,其发生子宫内膜癌的可能性是否至少是未服用者的2.8倍,则意味着假设检验(1)式中的δ0需改为2.8,此时有趣的现象发生了.对于Delta检验和Score检验,它们的检验p值分别为0.064和0.061.对于IM检验,其合理性函数的值为0.081.因此,在5%的显著性水平下,这3 种方法均不能得出拒绝原假设的结论.换句话说,为了得到女性服用结合雌激素,其发生子宫内膜癌的可能性是否至少是未服用者的2.8 倍的结论,需要更多的试验数据来支撑.然而事实上,对于RIM检验方法来说,却有32.9%的可能性得出拒绝原假设的结论.因为当随机权重w<0.329 时,随机化合理性函数的值将不超出0.05.因此,在本例中虽然并未获得更多的试验数据,但是通过RIM检验可以得出女性服用结合雌激素,其发生子宫内膜癌的可能性至少是未服用者的2倍提升至2.8倍.从这个角度而言,RIM检验告诉人们更多有用的信息.这个有用的信息对进一步揭示女性服用结合雌激素与其发生子宫内膜癌的真正联系具有重要价值. 推断模型(IM)旨在发展一种新的统计推断框架.它是一种合适的无先验的概率统计推断模型.感兴趣的读者可以进一步参考关于IM体系的文章[9-12].事实上,构造合适且有效的假设检验准则仅仅是IM体系的一个“副产品”.然而,Liu和Martin[7]所建议的关于“默认”的联结模型的构造可能无法得到离散情形的有效检验.本文利用随机联结模型[13-14]将试验数据和未知参数联结起来,并利用基于随机合理化函数的RIM检验进行决策.RIM检验已经被证实不仅是合适的而且是有效的.本文中还展示了RIM检验在配对试验中基于优势比的非劣检验中的运用,结果显示RIM检验比起频率学派和贝叶斯学派的方法更优.因此,实际上,推断模型在检验的有效性方面比起传统的方法更有优势. 关于运用随机检验(randomized tests)来解决离散模型中参数检验问题的历史已有很长时间了.对于二项分布和其他的离散分布中,事实上存在所谓一致最优势(uniformly most powerful,UMP)检验,包括UMP单侧检验和无偏UMP双侧检验(Lehmann[15]).上述检验都是最优检验步骤.然而,这些随机化检验在实际生活中几乎没有运用,主要是因为实践者反对在同一个具体问题中,对于相同的数据,由于随机化的原因却给出了不同的决策准则. 本文中,虽然基于推断模型得到的RIM检验也是一种随机化的方法,但它却是以一种简单直观的方法呈现出来.因此,是时候以另一种方式重新考虑随机化检验了:对于离散模型,由于离散分布的本质特点,所观测到的数据可能不是“完整”(full)的或“完全”(complete)的数据,在某种程度上只能把这些数据视为不完全数据(incomplete data).为了运用UMP检验,实践中需要从(0,1)上找到一个随机数来“完善”(complete)这些不完全数据.可能有些读者会有争议:因为两个统计学家分析同样的试验数据、运用同样的检验过程却得到不同的决策结果.为了澄清这样的疑惑,对于离散的模型,本文以另一个视角来解释随机化检验:或者随机化的检验过程并不是“完全一样”的,或者离散模型的数据是丢失部分信息的不完全数据. 事实上,随机化方法经常被运用在统计决策理论(theory of statistical decision)和博弈论(game theory)中,以提高决策的质量.而假设检验问题实际上也可视为普通决策理论的一种特殊情形,并且本文所提出的基于RIM 检验的决策准则也可视为一种随机决策函数(randomized decision func⁃tion).因此,我们认为随机决策函数应该在统计决策中发挥出应有的应用价值,而不是束之高阁,并且随机化决策思想的数学理论基础应该是后续统计理论研究的一个方向.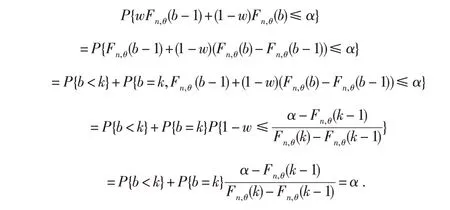
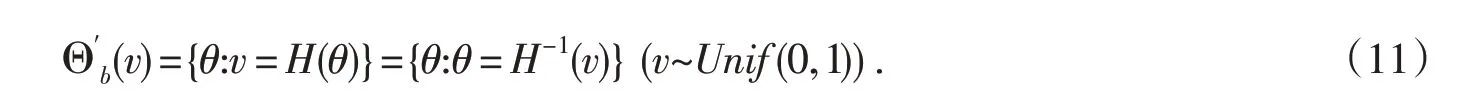
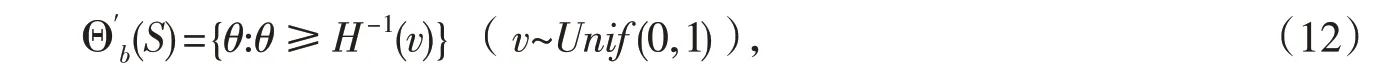

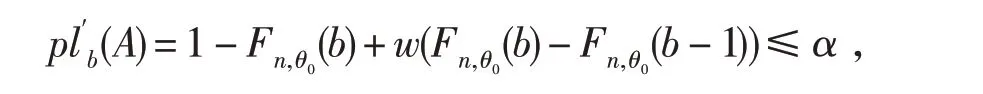

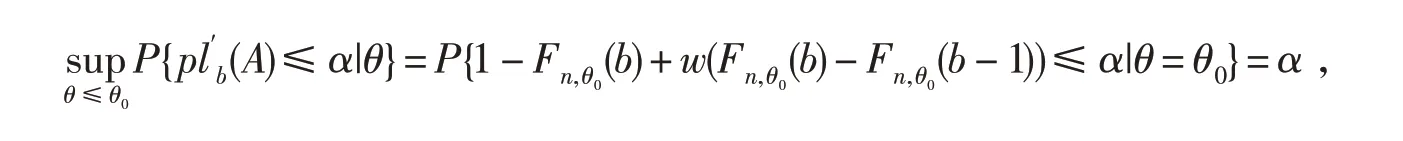
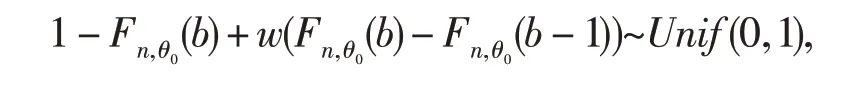

2 模拟研究
2.1 第一类错误率比较


2.2 统计功效比较

3 实证研究

4 结论

