放置状态及变参数对热声不稳定工作特性分析

刘浩哲, 严红

(1.航空工业西安飞行自动控制研究所, 陕西 西安 710000;2.西北工业大学 动力与能源学院, 陕西 西安 710072)

热声不稳定现象普遍发生在航空发动机、火箭发动机和燃气轮机等高性能动力装置中，这一现象很早就引发了国内外的探究[1-6]。早在1878年，Lord Rayleigh[7]就定性解释了热声振荡即热释放脉动与管内声学脉动之间耦合造成一种热声振荡现象。但由于热声学集合了声学、传热学、流体动力学等多个学科，导致其研究内容复杂，研究难度大，故对于热声振荡机理的完整解释至今仍存在较多困难。

Rijke管是典型的热声不稳定系统，由于其结构简单，故经常被用于燃烧热声不稳定性的机理研究[8-10]。陈福连[11-12]发现热声频率与Rijke型燃烧器的尺寸，形状和气体温度分布有关，与燃料性质无关，且当声能在管内的耗散等于声强梯度的负值时，系统就维持热声振荡的状态。韩飞等[13]用电加热放热的经验公式发展了一种预测热声不稳定发展的模型，且模拟结果与实验结果基本一致。慕尼黑工业大学Hantschk等[14]通过设立恒温板叠，首次对Rijke管内起振进行了模拟，并对管内高次谐频与换热规律结合进行研究。清华大学严红等[15]采用TVD格式模拟燃烧器，对管内的二维脉动流场及温度场进行分析，在入口加入周期性脉动速度，但与实际情况的自激振荡有不符之处。浙江工业大学钟英杰等[16]对Rijke型燃烧器研究，采用内外流场耦合的建模方法研究了Rijke管内流场，得到管口压力及声泄漏值，发现两端收口燃烧器对燃烧器设计有参考意义，但也因此造成计算量大大增加。浙江大学李国能等[17]对水平四分之三波长Rijke管计算模型使用多孔介质热源模型进行模拟，分析了工管内各参数对管内振荡影响的热声振荡规律。Rijke管作为燃烧不稳定的基础，如果要进一步应用于各动力装置中，就必须考虑变角度工作对燃烧室振荡的影响。现有的变角度Rijke管实验大多无法实现起振[18-20]，这就需要从数值模拟方面尝试对该实验中产生的热声机理进行解释。本文基于CFD采用数值模拟方法，对3种不同放置态下的Rijke管热声不稳定振荡进行考察，并通过对比三者间的振荡参数进而分析重力对热声振荡现象的区别及影响，以及由重力产生的热浮力对管内振荡的影响，并对加入温度对动力黏性系数和导热系数的变参数影响进行对比考察，提出了多模态及变参数对Rijke管振荡的具体影响及结论。

1 数学模型

本文在Kunz[21]的实验装置基础上发展了Hantschk和李国能构建的物理模型。实验采用方管，但前人研究[22-24]表明，当管声波波长和方管截面最大尺寸比小于0.5，方管内声波传播可认为与圆管相似。

模拟的Rijke管如图1所示，二维计算区域长0.989 m，宽0.015 8 mm。实验中加热丝得到的平均加热功率为54.5 W，在模拟中对应设置的加热丝温度为745 K。左端进口截面为声学封闭端，给定均匀的进口速度为0.15 m/s；右端为声学开口，给定压力为101 325 Pa。由于实验中所采用的电热丝建模较为复杂，根据前人研究，在数值模拟中平行板叠代替热源，这种方式也曾被Hantschk采用。板叠置于管中间(x=0.495 m)，该模型对应第二阶热声不模式。由文献[25]结论可知，板叠间距取2～4倍热渗透深度较好，更易激发热声振荡，故选取对应孔隙率为0.63。另外，Heckl认为，压力在管口开口端存在辐射和反射，并不是严格的波节，但由于管口效应对管内振荡影响不明显，故在本文中对此均做以简化。由于主要探究的是放置状态对Rijke管振荡的影响，故考虑管壁绝热。模拟的工质为空气。所有模拟首先均进行稳态计算，待管内流场稳定后，进行非稳态计算，在入口给定大小为100 Pa的瞬时扰动[15]。

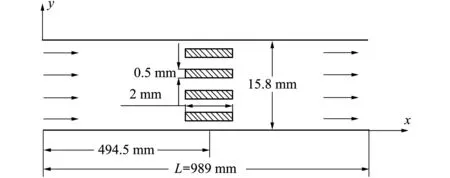
图1 物理模型图

2 计算结果及分析

本文首先对3种不同放置状态下的Rijke管进行考察，设置3种放置状态时主要通过设置商用软件Fluent17.1中重力加速度选项。对于忽略重力状态，即不对该项设置，而竖直放置和水平放置的设置依次对应为x=-9.8 m/s2和y=-9.8 m/s2。

另外，本文依次考察了动力黏性系数和导热系数对管内振荡的影响。具体参数设置在气体特性中对黏性系数设置为萨特兰公式，并对导热系数采用分段多项式置入参数。

2.1 不同放置对Rijke管振荡影响及分析

2.1.1 忽略重力下Rijke管振荡变化

图2给出管中心位置处(x=495 mm，y=7.9 mm，后述监测点统一为此)的压力和轴向速度的起振，最终达到极限周期的整个过程。值得注意的是，初始的100 Pa扰动只作用在瞬间，在下一个时间步长已经不再存在[16]。

通过对图2分析，发现Rijke管内压力和轴向速度，两者均在约1 s后迅速加强。在2.7 s时管内各项参数振荡均呈现饱和状态，热声学称之为极限周期。其中，压力振幅已超过600 Pa；速度振幅为0.43 m/s。温度和密度的振荡分布与前两者类似，故在此不再赘述，且温度振幅约为24 K，气体密度振幅则为0.042 5 kg/m2，这一结果也符合设定的理想气体公式。通过快速傅里叶变化捕捉到的管内频率为298 Hz。

图3给出了管内压力和速度的相位分析和压力与密度的相位分析。可以看出，压力峰值领先速度峰值0.000 88 s，对应角度为93°，故管内压力领先轴向速度四分之一周期，这也符合瑞利准则。根据图中的参数对比，发现压力与温度也基本同相，这也从侧面说明在最大压力输入热量，在最小压力时抽取热量可维持系统的达到极限周期时的热声振荡。

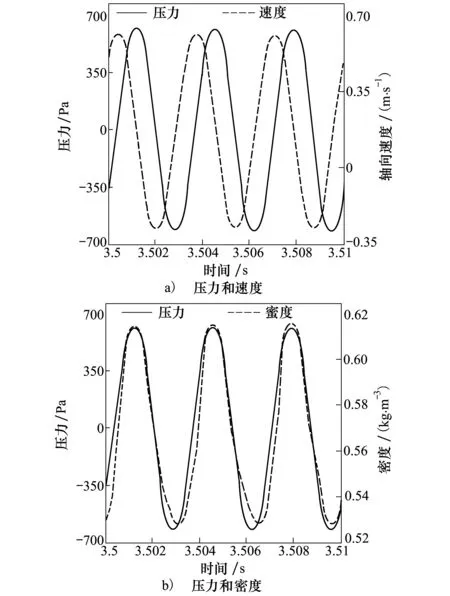
图3 忽略重力时的相位分析

2.1.2 竖直放置下Rijke管振荡变化

与前述对应，本章结果是在仅考虑动量方程中x方向质量力的基础上得到的[17]。因此本文着重考虑管内关键参数压力的变化，其他参数之后不再赘述。

图4给出了竖直放置时，Rijke管中心位置处的压力最终达到极限周期的整个过程。其中，压力振幅约为600 Pa。同样的，由图4中的压力振幅即可捕捉到管内振荡频率为298 Hz，与忽略重力时的频率相同。

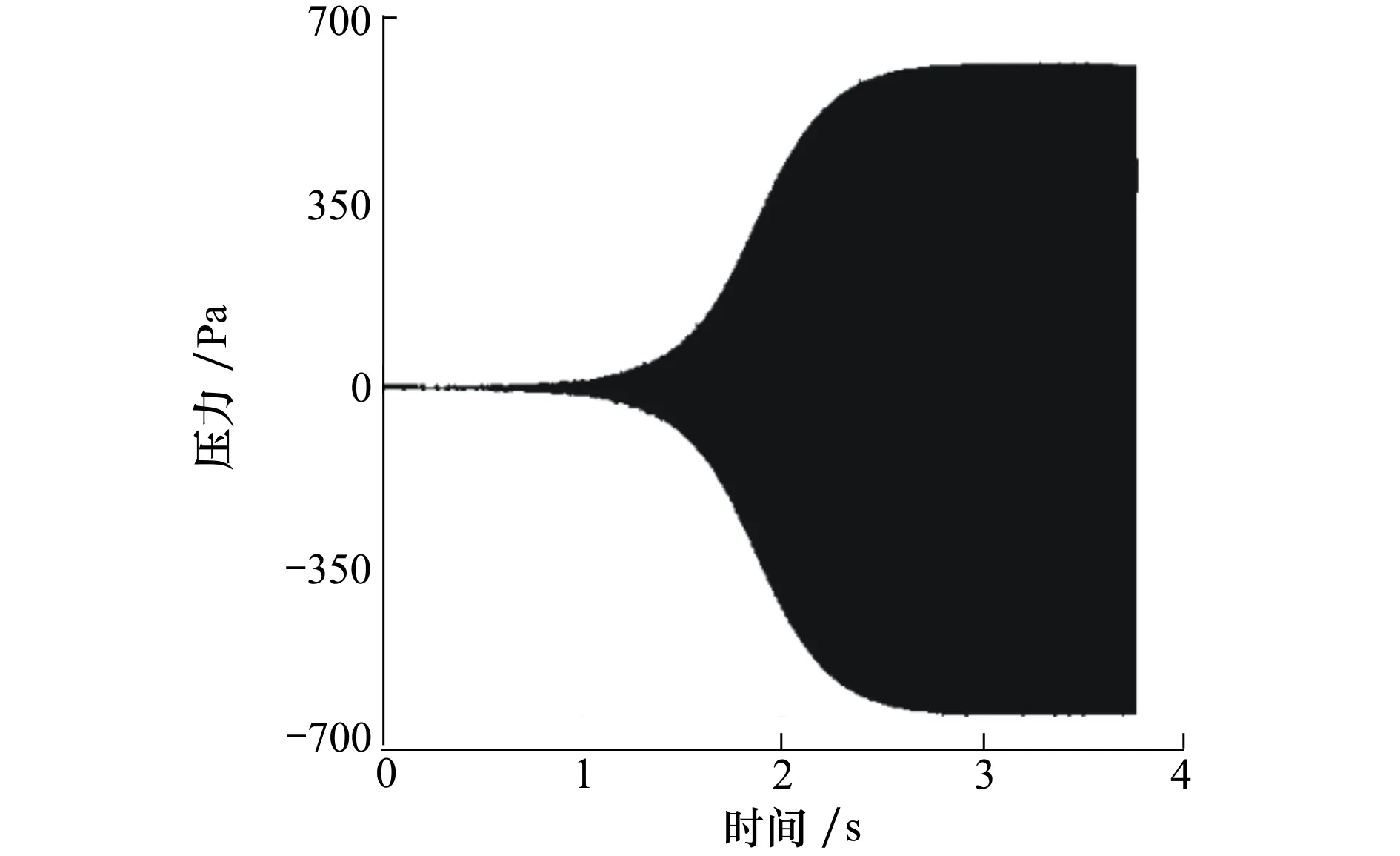
图4 竖直放置时的压力振幅

2.1.3 水平放置下Rijke管振荡变化

接着，在仅考虑动量方程中y方向质量力的基础上得到管内压力振荡变化。其中，图5给出了考虑水平方向时，Rijke管中心位置处的压力最终达到极限周期的整个过程。

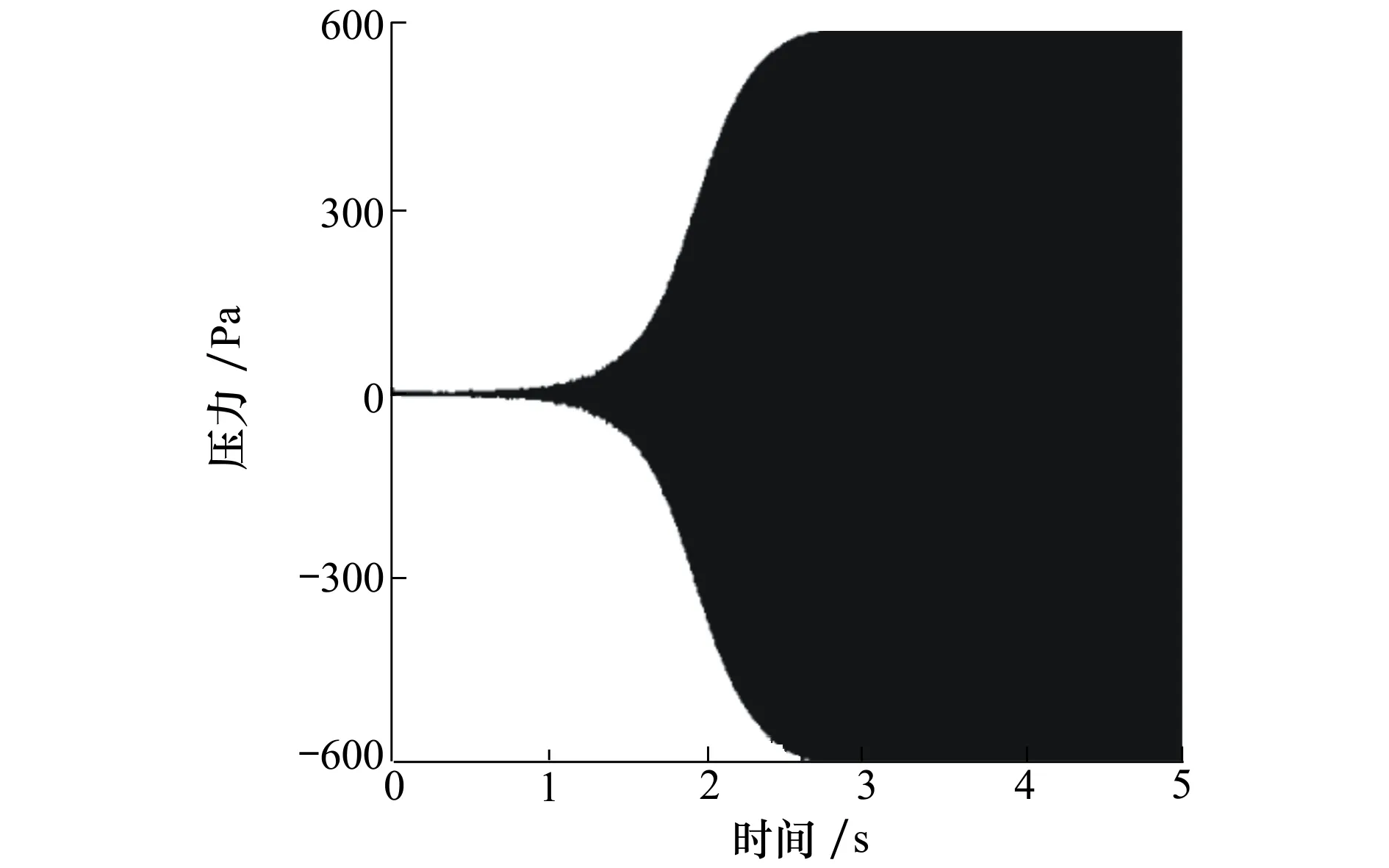
图5 水平放置时的压力振幅

其中，压力振幅略小于590 Pa。同样，可捕捉到管内频率为297 Hz，与前述2种情况的频率基本一致。这也证明无论是何种放置情况，基本对振荡频率没有影响。实际上，对于封闭开口的声学系统的热声频率解析解为f=c/l(不考虑模态的情况下)，其中c为声速，l为管长。且同一气体的声速随温度和压力变化很小，故多数情况下，管内压力频率变化并不明显。

但仔细对比可发现图2和图5存在较明显的变化区别。图2的振荡中从过渡段至极限周期的过程中存在较明显凸起，之后压力振幅存在较小程度减弱。这主要是由于在忽略重力时，板叠附近温度梯度较高，不存在由于气体重力产生的机械耗散，这部分热量在短期内无法与管内最终达到稳态的振幅相平衡，故在达到饱和后振荡通过减小振幅的耗散形式来达到管内真正的平衡，这一点与图5有较大区别。图5在这个过程中的变化相对平滑，这也印证了由于重力产生的机械振荡耗散会使得达到平衡的时间缩短且不会出现凸起，整个过程平缓有序。

图6是将忽略重力、竖直放置与水平放置3种情况的压力振幅进行对比。显然，前2种情况下压力变化基本一致。但进一步观察发现，饱和后竖直方向比忽略重力所产生的压力略大约5～10 Pa，这主要是由于重力方向产生的热浮力会促进振荡，进而增大压力振荡的幅值。

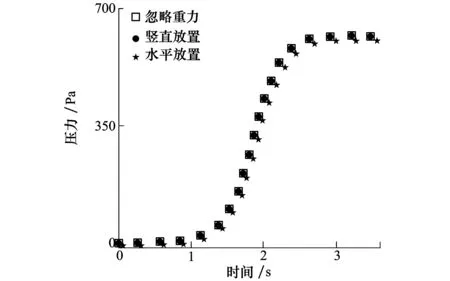
图6 3种放置状态时压力振荡情况

进一步比较水平放置下与前两者的压力情况。发现水平放置时，压力从起振时比忽略重力及竖直放置时的压力振幅均要小且起振时间变长。在达到饱和后明显比忽略重力下的压力要小一些，并一直在保持。仔细观察可以发现，在即将达到饱和时，水平放置明显比前两者的压力均要小约20～30 Pa，且在饱和后继续维持这个压力差。另外如前所述，竖直放置和水平放置过渡段的变化基本一致，在此不再赘述。

通过之前的对比发现，竖直放置与忽略重力的压力振荡幅值基本相差不大。但由于气体需要克服重力振荡，导致竖直放置时的压力振荡与速度振荡均相比于忽略重力时两者的情况会变小，且振荡也不如水平放置时剧烈，虽然竖直放置会有热浮力影响，但因此产生的速度也相对入口速度较小，对于振荡影响不明显。而对于水平放置，由于重力产生的加速度与入口速度进行叠加导致的结果是总体运动趋势向管口的两边，进而会使得振荡变慢，振幅减小，导致起振相对忽略重力慢一些。而重力产生热浮力的影响也必然会导致管内压力速度分布的不均，即管的下端堆积的气体更多，且热源附近的温度较大，热浮力明显，远离热源的位置热浮力减弱。综上所述根据所得结果，发现重力对管内振荡剧烈程度的影响要比热浮力所导致的热声振荡影响大，至少从结果看影响有限。

Kunz的实验如前所述，其实验结果在表1中给出。而浙大的李国能则采用Fluent6.1对Kunz结果进行数值模拟，本文在设置上与其一致，仅在热源作以优化，将多孔介质修改为平行板叠。根据表1对比，发现结果与实验基本相符，但均存在一定差别，由于实验需要在管壁打孔对各参数进行测量，且测量设备不可避免地存在一定的阻尼，故会导致模拟结果与实验的误差。而文献结果之所以在振幅上相差巨大，主要是由于其所建立的多孔加热介质模型不够精确。而本文在考虑热渗透深度的基础上仅仅加入十个板叠，在对流换热时必然导致更多热量散失，进而使得振幅降低，且由于本文网格设置相比文献要稀疏，结果会影响计算精度。但由于本文着重考虑各因素和参数带来的规律性，故结果对规律影响不大。

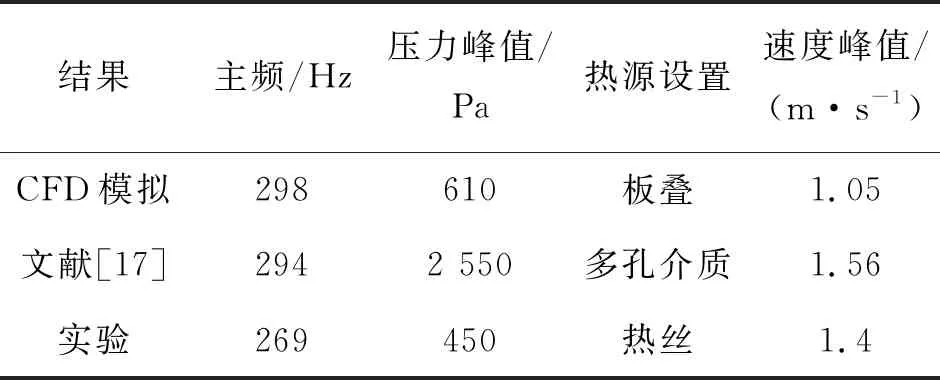
表1 水平放置CFD模拟与文献及实验对比

在结果对比中，数值模拟结果基本满足要求，为之后的参数计算提供可靠性保证。

2.2 黏性系数对Rijke管振荡影响及分析

前述工质为空气，故模拟时黏性系数恒定为μ= 1.724×10-5kg/(m·s)，但在实际管内振荡过程中，管内气体黏性系数一般会随着温度增大而增大。为精确考察黏性系数对Rijke管振荡全过程影响，探究影响管内振荡其他因素，在模拟中加入萨特兰公式(Sutherland formula,SF)。通过该式可得不同温度下对应的黏性系数，且适用范围为T<2 000 K。其中，μ0为参考值，一般为1.716×10-5kg/(m·s)，T0为参考温度，一般为273.11 K，s为有效温度，一般为110.56 K。

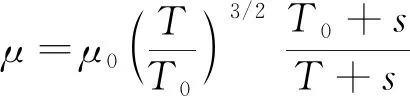
(1)

现仅通过对比忽略重力时在加入萨特兰公式前后，Rijke管中心位置处的参数变化，进而分析黏性系数对热声振荡的影响。由图7可知，其基本变化与图2相似，图中压力振幅约为385 Pa，温度振幅为16 K。且其第二阶热声不稳定的模式频率约为296 Hz，略低于黏性系数为定值时的频率。对于压力来说，发现加入萨特兰公式后的管内振荡明显变慢。

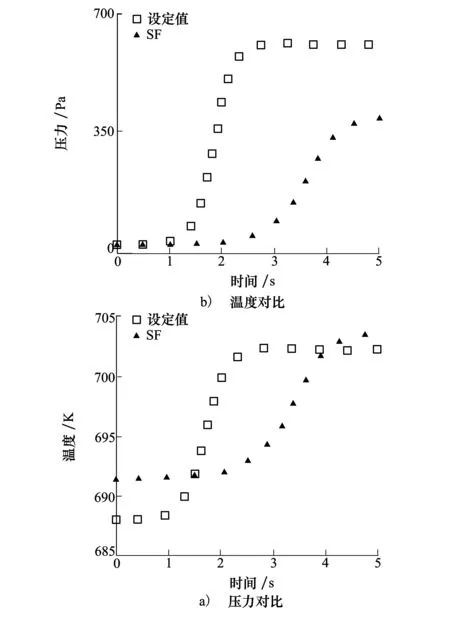
图7 萨特兰公式与黏性系数为定值时的参数对比

黏性系数为定值时，Rijke管约在2.7 s达到饱和，但加入萨特兰公式后，管内在4.9 s后才达到饱和。且振幅相比黏性系数为定值的小了约200 Pa。同样对于速度来说，萨特兰公式下的振幅相对黏性系数为定值时的振幅小了约0.2 m/s。

总的来说，由于萨特兰公式中，管内黏性系数随着温度变大，故当温度增大时，管内的损耗也同时增加，为了维持管内振荡，因此导致振幅会减小，管内振荡程度减弱。因此管内需要较长时间进行调节振荡饱和后的情况，故达到饱和的时间相应增加。

但值得注意的是，对于温度，虽然加入萨特兰公式后，管内振荡温度明显减小，振荡减弱，但振荡温度的最大值比之前要略微大一些。这是因为，虽然黏性系数的增大导致机械能以热量的形式耗散，但这部分热量并不会很快从管内出去，所以这部分热量会继续堆积，由此导致管内的温度会适当增大。在此，密度与温度变化规律一致，因此不再赘述。

2.3 导热系数对Rijke管振荡影响的变化

除黏性系数以外，导热系数对管内振荡的影响同样较大。前人一般在不影响结果分析的基础上，将导热系数扩大十倍来加速模拟计算过程。但实际上导热系数同样会随着温度的增大而增大，为更确切地得到贴近实际的结果，在萨特兰公式基础上，根据手册[18]提供的经验公式加入导热系数随温度变化的经验关系式,λ=A+BT+CT2，其中λ为导热系数A=0.005 12，B=7.234 2×10-5，C=-9.220 7×10-9，温度适用范围200 K≤T≤1 500 K。

在萨特兰公式基础上，加入导热系数随温度变化影响下，忽略重力时Rijke管中心位置时各项参数变化也不再赘述，其中压力振幅约为1 000 Pa，速度振幅为0.6 m/s，温度振幅为30 K，密度振幅为0.046 kg/m3。且管内各参数均明显相比之前振荡加快，约在0.5 s开始快速起振，饱合后振荡剧烈。进一步对压力做快速傅里叶变换，得到频率为302 Hz。相比之前同种工况下的频率明显变大，说明导热系数通过影响管内温度进而改变管内频率情况。接着，在考虑萨特兰公式的基础上，即黏性系数随温度变化时，再将导热系数为定值和考虑导热经验公式的2种情况进一步比较。

如图8a)所示，发现当导热系数随温度变化时，无论从其起振时间还是饱和状态下的振幅，都要远大于导热系数为定值时的情况。对于压力，当导热系数为定值时压力振幅仅不到400 Pa，但当导热系数随温度变化的时候，其振幅比其2倍还要大，且达到饱和的时间缩短了约二分之一。

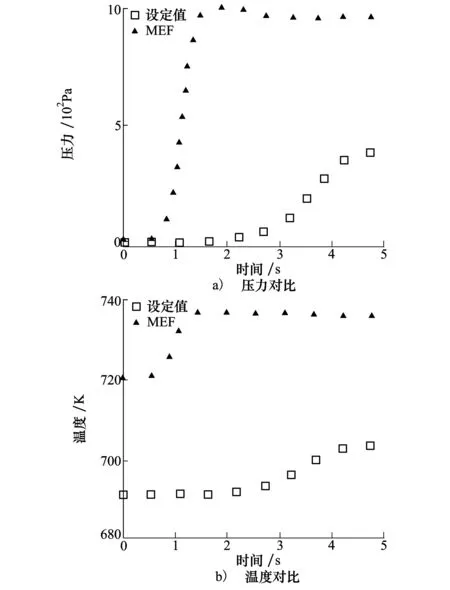
图8 萨特兰公式下导热系数随温度变化与定值时的参数对比

对比图6发现，当黏性系数和导热系数均为定值时，其压力约为600 Pa，达到饱和的时间约为2.7 s，萨特兰公式不仅减小振幅且拉长了饱和时间，虽然如此，当导热系数和黏性系数均随温度变化，占主导仍然是导热系数，其不仅加快达到饱和的时间(从2.7 s加快到1.6 s，且振幅从600 Pa增大到接近1 000 Pa)，这也充分说明导热系数对于热声振荡的影响要比黏性系数的影响大。这一点通过温度的振荡情况更加明显，在图8b)比对中可以发现，当导热系数随温度变化时，其起振开始的温度远超导热系数为定值时的温度，约从720 K就开始起振，而导热系数为定值时的起始温度仅为691 K，温度提高了约30 K，且振荡剧烈，振幅超过30 K。

但前述中，导热系数和黏性系数均为定值时，其温度振幅仅为20 K，振荡情况不如前者剧烈，且起始温度更低。如之前所述，这充分证明了导热系数是决定热声振荡的主导因素，因此在工质及管材料的选取上，通常需要选取导热系数随温度变化大，黏性系数则随温度变化小的材质，但文章仅探究工质为空气时的情况，对应其他工质及管壁的耦合选取还需进一步讨论。另外，这也说明当考虑导热系数随温度变化的情况下，会让三者振幅在极短的时间内快速增加，达到极为剧烈的振荡强度，并且会增大水平状态下的振幅，从而缩小振幅方面的差距。

图9是忽略重力下，考虑黏性系数和导热系数随温度变化与否综合影响的情况。

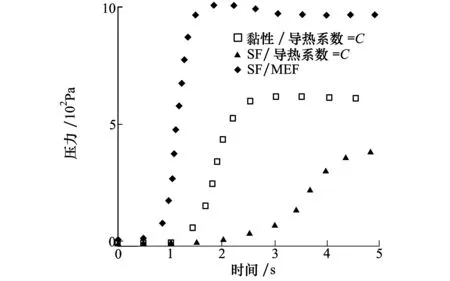
图9 忽略重力下黏性系数和导热系数对压力影响

从图9可以更加直观地看出当黏性系数随温度变化且导热系数为定值时比两者均为常数时的振幅缩小0.53倍，而比两者均随温度变化缩小1.05倍，倍率净变化49.5 %。这一结果远远超过黏性系数自身带来的影响。导热系数单纯对振荡幅值的提升及其显著。

3 结 论

本文以Rijke管为研究对象，基于二维可压缩NS方程及理想气体状态方程，采用数值模拟方法对Rijke管内的热声振荡进行了从起振到饱和状态的全过程数值模拟研究。通过考察3种不同放置状态对Rijke管内热声不稳定特性的影响，研究了重力以及随温度变化的动力黏性系数和导热系数对热声振荡现象影响，得到以下结论：

1) 忽略重力与竖直放置时刻的热声振荡情况基本一致，但水平放置下的热声振荡要相对小一些。由于重力本身产生的加速度会阻碍振荡，且热浮力产生的速度则会激励热声振荡，结合上述分析发现重力对管内振荡剧烈程度的影响要比热浮力所导致的热声振荡影响大。另外，忽略重力时压力过渡段存在凸起，这是由于此时比另外两者的板叠附近温度梯度高，因此在达到饱和后振荡通过减小振幅的耗散形式来达到管内平衡。

2) 加入萨特兰公式后，其结果与黏性系数为常数时的变化规律较为接近，但各参数差值都增大一倍。这是由于萨特兰公式下的耗散增强，振幅变小。由于黏性影响使得其振荡速度也会变小，更加影响热声振荡达到饱和的过程。这在文献的实验中有明显变化，即阻尼系数对振荡的具体影响。

3) 在结论2)基础上，考虑导热系数随温度变化的情况，发现依然会让管内振幅在极短的时间内快速增加，达到极为剧烈的振荡强度，并且会减小忽略重力下的振幅，从而缩小振幅方面的差距。对于两者综合比较的模拟情况，在之前文献中未见此方面研究。当黏性系数随温度变化且导热系数为定值时比两者均为常数时的振幅缩小0.53倍，而比两者均随温度变化缩小1.05倍，倍率净变化49.5 %。这一结果远远超过黏性系数自身带来的影响。