基于带RBF核的SVM模型对红酒品质的精准分类
李琴,朱家明,郎红,宋国锋
(安徽财经大学统计与应用数学学院, 安徽 蚌埠 233030)
0 引言
随着人们生活水平的不断提高,近年来,红酒已然成为了大众的日需品,使得红酒产量不断加大,同时关于红酒品质的鉴定也是一大问题.传统的人工品鉴存在很多弊端,人工品鉴没有统一的评估标准,效率低、易导致较大误差、且成本较高.故根据红酒的各项理化指标,对红酒品质进行精准鉴定,探究不同理化指标对红酒品质的作用效力,以此为目的建立数学模型,进行探究分类预测,对红酒企业提高红酒品质、减少品质错评误差、提高企业竞争力有很大的现实意义.同时,解决如何精准预测红酒品质鉴定的问题在节约成本、调高效率方面也具有重要意义.
基于以往的红酒品质分类问题和典型分类模型研究,梁书绮[1]通过收集大量数据,运用朴素贝叶斯原理以及机器学习,构建基于朴素贝叶斯原理的红酒品质预测模型,在小错误率下对其进行准确预测,证明了朴素贝叶斯算法在红酒品质预测中的实际实用性.刘攀[2]则通过利用RBF神经网络和朴素贝叶斯分类算法相结合的机器学习理论构建分类模型来提高红酒品质分类的准确度,并通过改进算法发现该方法具有较高的分类精度,但泛化能力不理想.毕艳亮等[3]使用人工智能理论中的BP神经网络构建分类模型,实现对红酒品质的高效分类,虽使用改进的遗传算法对其优化后,分类效果显著,但分类准确率还有待提高.聂树林和姚仰新[4]基于Beyes思想与RBF核结合的B-RBFN分类器进行一定数量的样本算法学习之后达到了较好的分类性能,且给出较具体的“属于”参数.朱芳等[5]采用改进的网络搜索法选取核参数,通过UCI数据集验证了带RBF的SVM模型的有效性,较其他核函数更具优势.
本研究针对以往红酒品质分类过程中复杂且低效的问题,使用带RBF核的SVM模型解决数据分类问题.同时在挖掘不同因素重要程度上,通过将RFE、深层次回归分析和ANPVA结合,构造作用效力挖掘模型进行研究.
1 数据来源及假设
本研究数据来源于2020宁夏大学生数学建模竞赛E题,依据红酒的11个理化指标[14]:酒精的浓度、pH 值、 糖的含量、非挥发性酸含量、 挥发性酸含量、柠檬酸含量、氯化物含量、游离二氧化硫、总二氧化硫、密度、硫酸盐含量,来综合评价红酒品质属于0~11的某个等级.为了便于处理问题,提出以下假设;1)数据真实可用;2)认为红酒的品质只受附件所给的理化指标影响;3)所有红酒在口感等方面一模一样,不影响品质;4)假设数据分布均匀.
2 相关模型、算法和建立求解
2.1 模型和算法1)带RBF核的SVM(支持向量机)模型[6].SVM(支持向量机)[7]是一种分类模型,它定义在空间中的一个可以将所有数据划分的超平面上,且使得所有数据集中到这个超平面的距离最短.例如a·x+b=0为分离超平面,对于线性可分的数据集来说,这样的超平面有无穷多个,但距离之和最小的超平面是唯一的.
针对带RBF核的SVM模型,其模型算法简单方便,可直接用于分类预测.模型整体准确率较高,且在面对较少样本时也能具有显著的准确率.在一定情况下,较准确的函数参数可以显著提高SVM模型的准确率,且大量训练集样本也可显著提高模型准确率.
2)作用效力挖掘模型.①深层次回归模型.回归模型是极其常见的探究多个自变量与因变量之间关系的模型.设有n个自变量分别为x1,x2,…,xn,因变量为Y,则建立多重线性回归模型,形如Y=β0+β1x1+β2x2+…+βnxn+ε,其中ε为误差项.
接着使用深层次回归分析计算相对权重,对所有可能的子模型中添加一个预测变量引起的拟合优度平均增加量的一个近似值,从而计算出每个自变量解释回归模型拟合优度能力,即得到各个自变量的相对重要性.
②单因素方差分析模型.单因素方差分析是指试验中只有一个影响试验指标的条件改变,并对试验数据进行分析,判断单因素对试验指标的影响是否显著.设单因素A有r个水平,分别记为A1,A2,…,Ar,在每个水平下,需考察的指标可以被看作是一个总体Xi(i=1,2,…,r),且Xi~N(μi,σ2).在各水平下进行ni次独立检验,样本记作如下所示Xij(i=r,j=ni),Xij~N(μi,σ2)且相互独立.
假设:H0:μ1=μ2=…=μr,H1:μ1,μ2,…,μr不全相等.
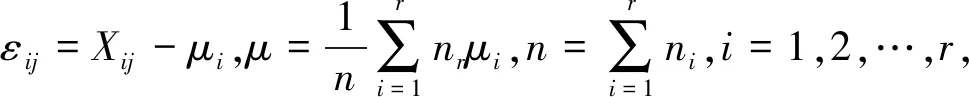
2.2 建模过程
2.2.1 SVM模型
1)数据预处理.首先,利用R将数据集中显示为“N”的设置为缺失值,进行行删除处理.同时利用R的as.numeric()函数将所有数据转化为数字型数据,供后续建模使用.接着使用递归特征删除模型[8],将红酒的理化指标进行筛选,并且为提高准确率,选择整个红酒品质数据集作为模型的训练集.
2)模型的建立.假设给定一个特征空间上的训练数据集T={(x1,y1),(x2,y2),…,(xn,yn)}.其中,xi∈Rn,yi∈{+1,-1},i=1,2,…,N,xi为第i个特征向量,yi为类标记,当它等于+1时为正例;为-1时为负例.
3)模型的求解.使用R构建带RBF核的SVM模型,将数据集中quality作为分类目标,其余变量作为判断标准,构建第一个普通SVM模型.接着,通过R中tune.svm()函数对SVM模型中的gamma参数值和cost参数值进行择优,拟合出新的SVM模型.通过带回红酒品质数据集进行对比分析,我们发现利用带RBF核的SVM模型的准确率高达74.01%,其中准确分类个数为2 862个,错误分类个数为1 005个.
同时,对错误分类的数据进行分类分析,我们发现数据的误差绝对值也大多为1,即错判致相邻品质的红酒数量,占比为23.89%,还有极少数错判分类误差绝对值为2或3的数据,占比分别为1.91%和0.18%.
2.2.2 作用效力挖掘模型 其模型示意如图1.

图1 作用效力挖掘模型示意图
1)数据预处理.首先,在进行RFE[9]指标筛选及后面的深层次回归分析,需要先将附件表格内的数据转换为数字型,通过R的as. numeric()函数即可进行快速转换.
2)模型的建立.首先根据递归特征删除进行红酒理化指标的筛选,接着构建回归模型,利用深层次回归分析[12]计算指标的相对权重,从而对理化指标的重要性进行描述并排序,得到影响品质的前三种理化指标.最后利用单因素方差分析,若不同品质间的红酒的三种理化指标皆具有显著差异,则可认为其对红酒品质分类有着显著性影响,即可证明结论成立[10].
3)模型的求解.首先,运用R进行递归特征删除,结果显示11种理化指标特征值相接近,说明无法剔除任何一种理化指标,即根据特征值,11种理化指标都是影响红酒品质分类值的重要因素[13].
于是对各指标的重要度进行分析,构建多元线性回归模型,利用深层次回归分析计算相对权重,得出影响红酒品质分类的前三个指标分别为alcohol(酒精)、density(密度)和volatile acidity(挥发性酸含量).其中alcohol(酒精)这一指标对红酒品质分类值的解释能力达到43%,density(密度)和volatile acidity(挥发性酸含量)的解释能力则分别达到20%和13%,如图2所示.
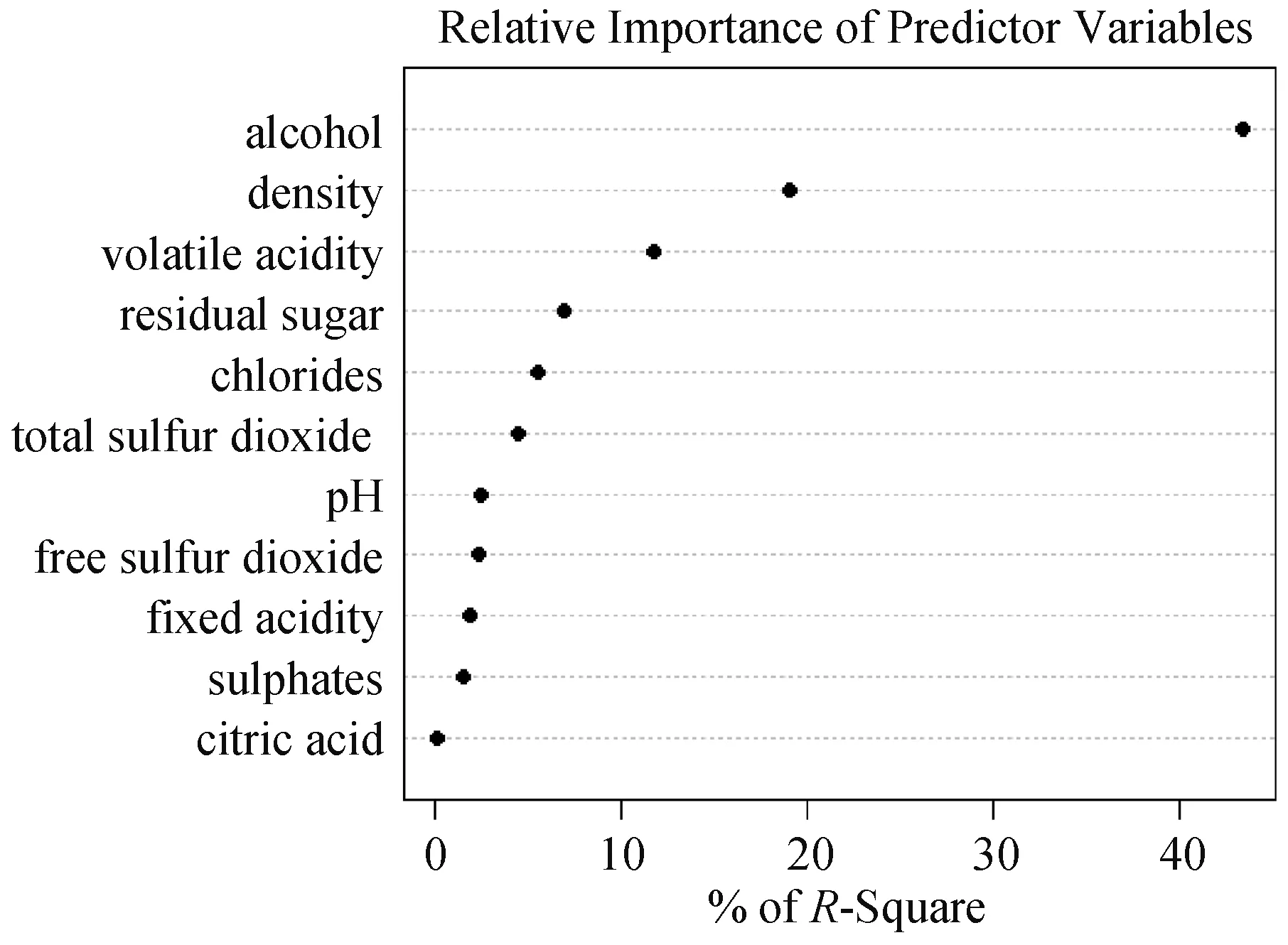
图2 各理化指标的重要程度
4)回归检验.分别通过对酒精、密度和挥发性酸含量三种理化指标数据进行ANOVE分析,验证以上结论,结果如下表1所示.结果显示,不同品质之间的酒精、密度和挥发性酸含量皆具有显著的差异性,即可验证上述深层次回归分析得到的结论.
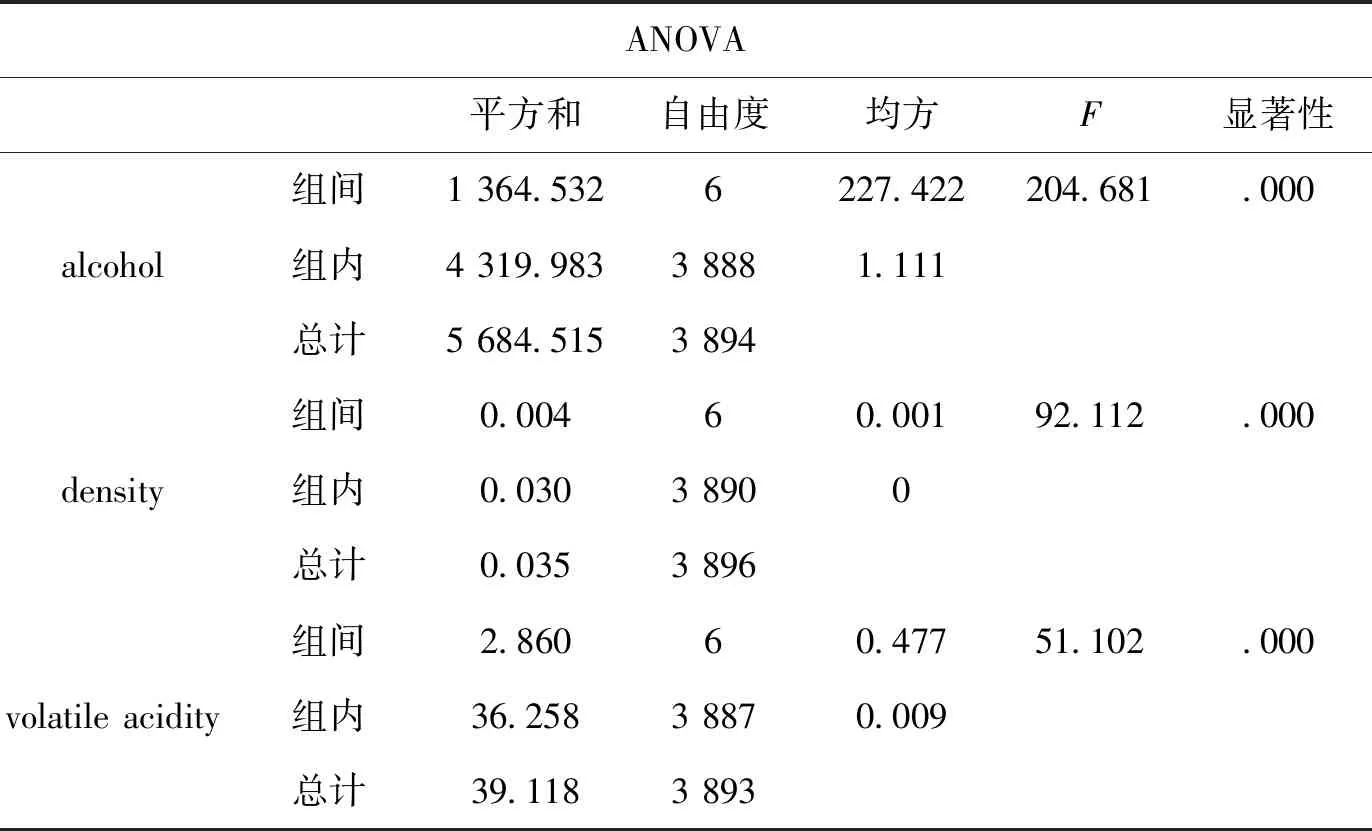
表1 方差分析表
3 SVM模型的改进
运用试点法,利用R分别构建gamma值为0.1,0.2,0.3,0.4,0.5,0.6的SVM模型,并分别对测试集进行分类预测.将附件中数据拆分为训练集和测试集,比例分别为70%和30%,使用相同训练集数据及不同gamma参数构建的不同SVM模型对测试集进行分类预测,并计算准确率和收集误差类型,从而进行误差值分析.
同时,通过绘制不同gamma值对应的SVM模型准确率趋势图,可以清晰看到,当不断增加gamma值时,其SVM模型的准确率也在不断上升,如图3所示.则说明,所提出的方法二,通过改变SVM的gamma参数值,可以提升SVM模型的准确率.
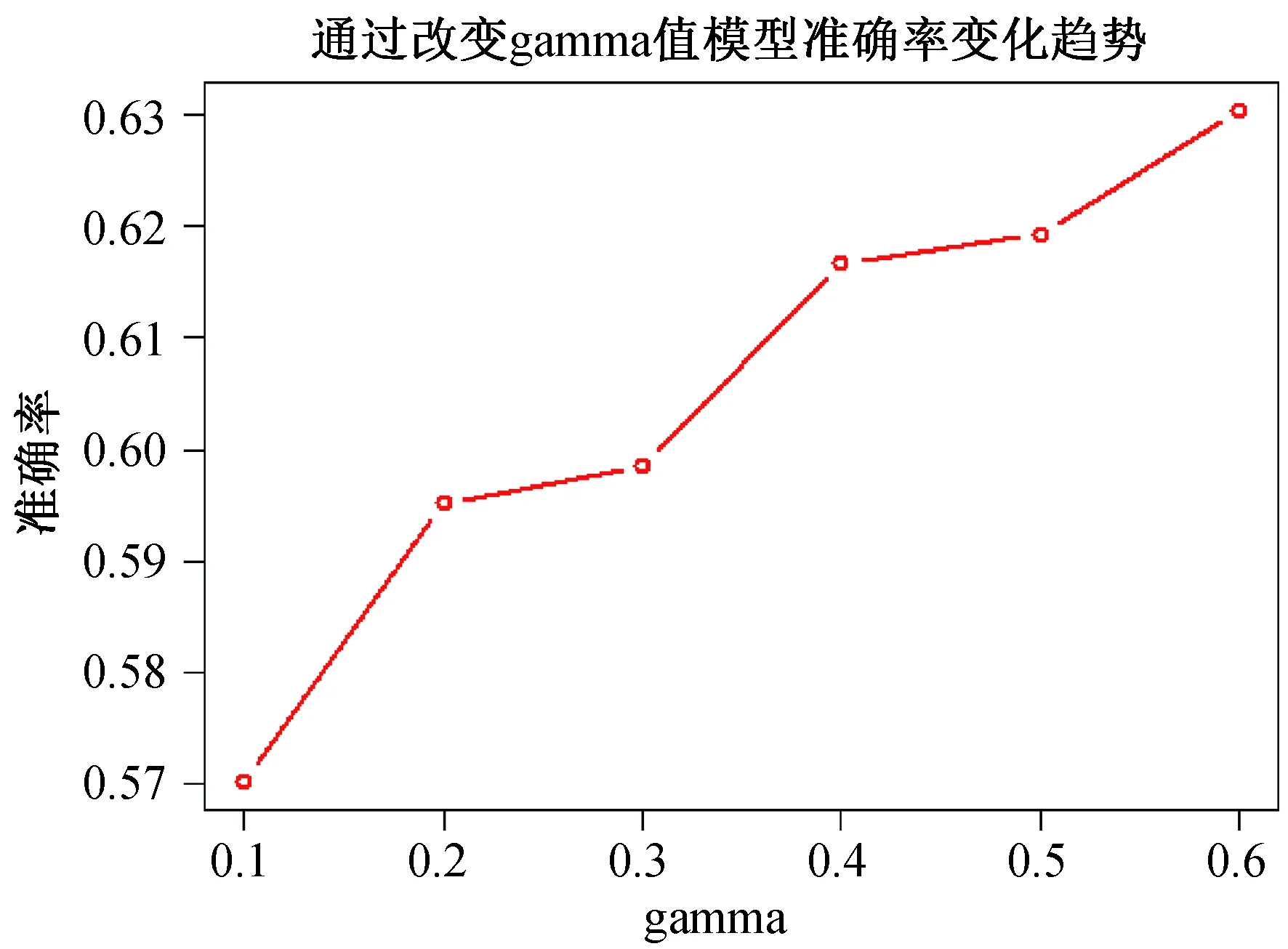
图3 不同gamma水平下模型准确率变化趋势
同时,对不同类型的误差值进行误差分析,可以发现改变gamma模型可以显著降低错判误差为1的数据.但同时,我们发现不同gamma水平下误差值为2和3的数据个数却并非呈现出单调趋势.
综上,我们通过分别对准确率和大误差进行赋权,构建出择优模型.
Z=100γ0-0.045γ1-0.25γ2-0.5γ3,
当择优模型达到最大值,所输出的gamma值即为最佳SVM模型的gamma参数值,如图4所示.

图4 舍去gamma水平的模型z得分
4 结果与分析
研究显示,利用带RBF核的SVM模型的准确率高达74.01%.同时,对错误分类的数据进行分类分析,我们发现数据的误差绝对值也大多为1,即错判至相邻品质的红酒数量.由此可说明SVM模型对红酒进行品质预测的结果具有较高的准确率,且SVM模型误差值小,能够在极大程度上避免产生以次充好、高品质被错判成差品质而导致的欺骗顾客、成本浪费的情况,对于红酒企业也具有现实意.
递归特征删除结果显示11种理化指标特征值相接近[15],说明无法剔除任何一种理化指标,即根据特征值,11种理化指标都是影响红酒品质分类值的重要因素.于是对各指标的重要度进行分析,构建多元线性回归模型,利用深层次回归分析计算相对权重,得出影响红酒品质分类的前三个指标分别为alcohol(酒精)、density(密度)和volatile acidity(挥发性酸含量).其中alcohol(酒精)这一指标对红酒品质分类值的解释能力达到43%,density(密度)和volatile acidity(挥发性酸含量)的解释能力则分别达到20%和13%.最后,分别通过对酒精、密度和挥发性酸含量三种理化指标数据进行ANOVE分析,以验证以上结论.结果显示,不同品质之间的酒精、密度和挥发性酸含量皆具有显著的差异性.
模型改进结果显示:当不断增加gamma值时,其SVM模型的准确率也在不断上升.则说明,所提出的方法二,即通过改变SVM的gamma参数值,可以提升SVM模型的准确率.最后发现当gamma值为0.6时,择优模型得到最大值,则可认为gamma区间为[0.1,0.6],gamma值达到0.6时,SVM模型分类精准率达到最优.同时,对不同类型的误差值进行误差分析,可以发现改变gamma模型可以显著降低错判误差为1的数据.但同时,我们发现不同gamma水平下误差值为2和3的数据个数却并非呈现出单调趋势.通过观察gamma值分别为0.4和0.5的得分可知,虽然gamma值为0.5的模型精准率高,但同时产生的大误差数量也多,所以在权衡比较z得分后,gamma值为0.4时的模型准确率更高,相比之下更优.
5 结束语
若取附件数据内不同品质的红酒的各项理化指标的平均值进行SVM模型构建,再次进行预测.结果显示,准确率能够保持在较高水平,数值为85.7%.同时其中错误估计的误差不大于1,对红酒品质错误判断也只会错判至相邻的品质,不会造成过分误差及损失,能够在极大程度上避免产生以次充好、高品质被错判成差品质而导致的欺骗顾客、成本浪费的情况.对红酒企业而言,这对营造企业形象、获取经济利益也具有现实意义.
基于SVM模型解决精准红酒品质分类问题的模型,可以进行拓展推广.本研究将改进的SVM模型用以解决分类问题,在原有的基础上显著提高分类准确率,对各大企业提高商品品质、减少品质错评误差、提高企业竞争力上有很大的现实意义.同时,解决如何精准预测不同商品品质鉴定的问题在节约成本、调高效率上具有显著意义.
此外,本研究将递归删除法、深层次回归分析及单因素方差分析相结合,构建作用效力挖掘模型,以此解决不同变量间作用效力的描绘排序.该模型针对经济、科技、农业、医学、环境乃至社会发展等方面的影响因素相关性分析上具有广泛的应用,如研究地区旅游经济的影响因素效力作用等问题.

