抗剪强度参数不确定性对库水及降雨作用下边坡可靠度的影响研究

何国顺 刘 飞 张 健 吕 平 王延磊

(1.北京建筑大学 土木与交通工程学院，北京 100044; 2.北京未来城市设计高精尖创新中心，北京 100044)

三峡库区地质条件复杂，在库水位骤降和降雨联合作用下容易发生滑坡灾害[1-3].目前国内外学者针对库水联合降雨作用下边坡的渗流稳定性进行了大量研究.梁鑫等[4]研究了库水位升降和强降雨作用下干井子滑坡的渗流、稳定性及应力-应变的变化规律，认为库水位下降是边坡稳定性降低的主要原因.张俞等[5]探讨了库水位骤降联合降雨作用下麻柳林滑坡的边坡稳定性，并进一步运用正交试验和极差分析法比较了黏聚力、内摩擦角和降雨量3个因素的敏感性.陈园等[6-8]对不同类型降雨联合库水位骤降下的边坡渗流稳定性进行研究，得出了降雨类型、库水位骤降速率对孔压和稳定系数的影响规律.

事实上，由于受到自然因素及人为因素的影响，土体内部性质存在较大差异，仅根据确定性安全系数评价边坡安全性是不够客观的，因此考虑不确定性的可靠度分析逐渐得到了重视.刘文洁等[9-10]在假定材料为同一变异系数并服从正态分布的前提下进行了库水、降雨作用下边坡的可靠度分析，比较了不同工况对失效概率和可靠度指标的影响.骆飞等[11]利用Monte-carlo法比较了不同抗剪强度指标变异水平对边坡安全系数和失效概率的影响，并给出了相应的可靠度指标与均值安全系数间的函数表达式.袁葳等[12]研究了抗剪强度参数空间变异性对边坡稳定性的影响，认为内摩擦角和黏聚力的相关系数与变异系数、失效概率成正比，且黏聚力的空间变异性对边坡稳定性的影响大于内摩擦角的影响.蒋水华等[13]针对无限长边坡在降雨作用下的失稳机理与可靠度进行了分析，认为土体渗透系数及抗剪强度参数的变异性会通过影响安全系数分布区域、滑动面位置的确定以及湿润锋的推进来影响边坡的稳定性.

为此，本文以三峡库区白家包滑坡为例，对库水联合降雨作用下的边坡渗流稳定性进行分析，在此基础上，考虑c、φ的不确定性，进行不同c、φ的变异系数与概率分布形式组合下的可靠度分析，得到了库水、降雨及c、φ不确定性相互作用下边坡的失效概率和可靠度指标.为边坡工程的设计与安全性评价提供参考.

1 计算理论

1.1 抗剪强度指标的不确定性

抗剪强度指标(c、φ)的不确定性主要体现在c、φ变异系数的不确定性、c、φ互相关系数的不确定性以及c、φ概率分布形式的不确定性3个方面[14].其中，变异系数δ通常被用来评价岩土样本的离散程度[15]：

(1)

式中：σ为标准差；μ为均值.

根据骆飞等[11]土体参数变异系数的整理结果，将黏聚力变异系数δc和内摩擦角变异系数δφ划分为小、中和大3个变异水平并给出了本文的计算取值，见表1.

表1 参数变异水平划分及计算取值

李亮等[16]通过研究发现，多数情况下c、φ存在较大的负相关性，而可靠度计算考虑其负相关性时，可靠度指标会偏大，故工程中不考虑c、φ的互相关性偏安全，本次计算取c、φ互相关系数为0.目前学者们普遍认为c、φ的概率分布形式为正态分布，然而陈立宏等[17]通过大量的计算和资料收集后发现，将非正态分布简化为正态分布会造成较大的误差，并建议当数据不充足时应采用对数正态分布.基于此，本文针对c、φ的不同变异系数、不同概率分布形式组合下的边坡可靠度进行了对比研究.

1.2 Monte-carlo法可靠度分析原理

Monte-carlo法分析滑坡的过程：选取滑坡的影响因素(主要有重度、黏聚力、内摩擦角、库水位升降速率、降雨强度、降雨类型、降雨持时等)以及它们的统计值和概率分布，将这些因素作为自变量，根据滑坡稳定的极限状态建立稳定性与影响因素的关系：

F=f(x1，x2，x3，x4，x5，x6，…)

(2)

式中：F为运用非饱和极限平衡理论计算所得的稳定系数；x1，x2，x3，x4，x5，x6，…为滑坡稳定性的影响因素.

利用Monte-carlo法对滑坡稳定性影响因素进行随机抽样，由式(2)算出每次抽样所得的安全系数Fi，重复进行，可得到N个独立的安全系数样本值F1，F2，…，Fn.F=1为极限状态，当F>1时，y=1为稳定；当F<1时，y=0为失效.若在N次迭代计算中，y=0出现了M次，则失效概率为：

(3)

其均值和标准差可表示为：

(4)

(5)

定义滑坡体的临界安全系数为μ′，可靠度指标可定义为：

β=(μF-μ′)/σF

(6)

在标准正态空间分布中，失效概率可定义为：

Pf=1-Φ(β)

(7)

2 案例分析

2.1 工程概况

白家包滑坡位于秭归县归州镇向家店村，距香溪河右岸河口2.5 km，距三峡大坝41.2 km，属于堆积体滑坡.滑坡纵长600 m，宽400 m，后缘高程275 m，前缘浸入香溪河，剪出口高程约为135 m，坡体平均厚度约为35 m，滑体面积约为24×104m2，体积约为840×104m3，其平面图及剖面线如图1所示.

图1 白家包滑坡平面图及剖面线

2.2 计算模型及参数

利用软件Geo studio2007建立计算模型如图2所示.

图2 计算模型

模型网格由四边形加三角形组成，共有节点4 380个，单元4 338块.整个模型划分为滑体、滑带和滑床3个区域，边界条件设定bc为定水头237 m，ab、cd为不透水边界，af为降雨入渗边界，def为库水位变动边界，并在滑体中设置了上(168，238)、中(293，200)、下(503，165)3个孔压监测点.

参考《白家包滑坡地质勘察报告》[18]并反复类比后得到土体基本参数见表2.鉴于模型的大部分区域位于地下水位以下，为简化计算，滑体和滑带的γ、c和φ采用饱和状态参数值，滑床为基岩.

表2 土体基本参数

2.3 计算工况设计

为研究库水位骤降及降雨作用下白家包滑坡的渗流稳定性，设置了工况①仅库水位骤降：库水位骤降速率分别为0.5 m/d、1.0 m/d、1.5 m/d；工况②库水位骤降联合降雨：库水位骤降速率为1.0 m/d，降雨发生在库水位骤降中的不同时间段(0～10 d、10～20 d、20～30 d)，强度为0.1 m/d，见表3.

表3 计算工况

3 边坡稳定确定性分析

3.1 孔压变化

如图3所示，随着库水位的骤降，坡内部分土体逐渐从饱和状态转变为非饱和状态，孔压逐渐消散，上、中、下3个监测点的孔压整体上都呈减小的趋势，且同一监测点库水位骤降速率越大的孔压减小越多；最终土体中稳定后的孔压大小以及孔压下降的幅度顺序均为：下部>中部>上部，这是因为前缘土体浸在库水中，受库水的影响最大；同时，由于滑坡土体渗透系数较小，土体孔隙水在库水位骤降过程中不能及时排出，上部和中部的孔压变化对库水位下降的“响应”有些滞后，且表现为距离库水越远的监测点滞后越明显；其中，下部监测点孔压在库水位骤降一开始便减小，中部监测点孔压在库水位骤降5 d左右开始减小，而上部监测点孔压在库水位下降14 d左右才开始减小.

图3 库水位骤降各监测点孔压变化

如图4所示，库水位骤降叠加降雨入渗后，3个监测点的孔压总体上仍呈现下降的趋势；最终土体中稳定后的孔压大小顺序仍为：下部>中部>上部，但孔压下降幅度顺序为：上部>下部>中部.值得注意的是，随着雨水的入渗，边坡表层土体迅速形成暂态饱和区，降雨停止后表层土体含水量又迅速减少，因此上部监测点和中部监测点的孔压在降雨刚开始和降雨刚结束时分别出现了“陡增”和“陡降”的现象，而下部监测点的孔压受降雨作用的影响较小.同时，在降雨期间以及降雨停止后的10多天里，上部监测点孔压几乎不变，存在“响应”滞后现象.

图4 库水位骤降联合降雨作用下各监测点孔压变化

3.2 安全系数变化

综合白家包滑坡的重要性及各种外部因素对其稳定性的影响程度，对白家包滑坡稳定性状况进行了划分(见表4).

表4 按安全系数划分白家包滑坡稳定性状况

如图5所示，在仅库水位骤降工况下，随着库水位的下降，边坡安全系数整体上呈先减小后增大的趋势；0.5 m/d工况下边坡始终为基本稳定状态，而在1.0 m/d和1.5 m/d工况下，边坡在库水位降至145 m左右时为欠稳定状态.同时，库水位下降速率越大，边坡安全系数降低也越快，所达到的最小值也越小，在库水位降至最低并最终稳定后的边坡安全系数反而越大.

图5 不同库水位骤降、降雨作用下边坡安全系数变化

库水位骤降联合降雨工况下的边坡安全系数同样表现出先减小后增大的规律，3种工况下边坡在库水位降至145 m左右时均为欠稳定状态，且总体上边坡安全系数的数值略小于仅库水位骤降工况下的边坡安全系数.可见，相较于库水位骤降工况，发生在不同时间段的降雨入渗对边坡稳定性的影响较小；其中，降雨发生在库水位骤降的10～20 d时，边坡安全系数达到的最小值最小，且在库水位降至最低后安全系数的变化趋于一致.

4 可靠度分析

表5为本次可靠度计算中滑体和滑带的土体参数的计算取值，同时以滑体为例给出了仅考虑c不确定性时其概率分布形式的示意图如图6所示.由于重度γ的变异系数较小，且对可靠度计算结果影响较小，本次分析不予考虑.将c、φ的变异系数与概率分布形式进行了不同组合，利用Monte-carlo法对工况①中的1.0 m/d库水位骤降和工况②中的1.0 m/d库水位骤降联合降雨发生在10～20 d的两种情况进行完全指定滑移面上的可靠度分析，抽样次数为10 000次，得到了边坡在各个库水位下对应的瞬态失效概率.

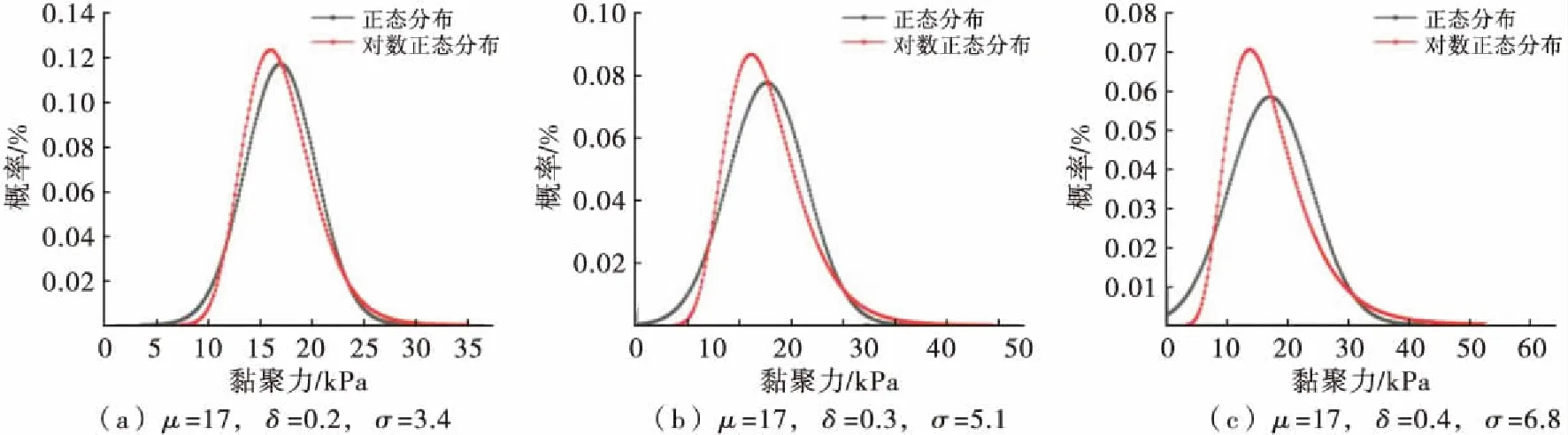
图6 概率分布形式示意图

表5 可靠度计算中参数取值

4.1 仅考虑c或φ不确定性时失效概率变化

参照徐卫亚等[19]依据失效概率对滑坡稳定性状况的划分得到了白家包滑坡的划分表(见表6).

表6 按失效概率划分白家包滑坡稳定性状况

如图7所示，随着库水位骤降和降雨入渗，边坡在各个库水位下对应的瞬态失效概率总体上都是呈现先增大后减小的趋势.其它情况相同时，变异系数越大失效概率越大.

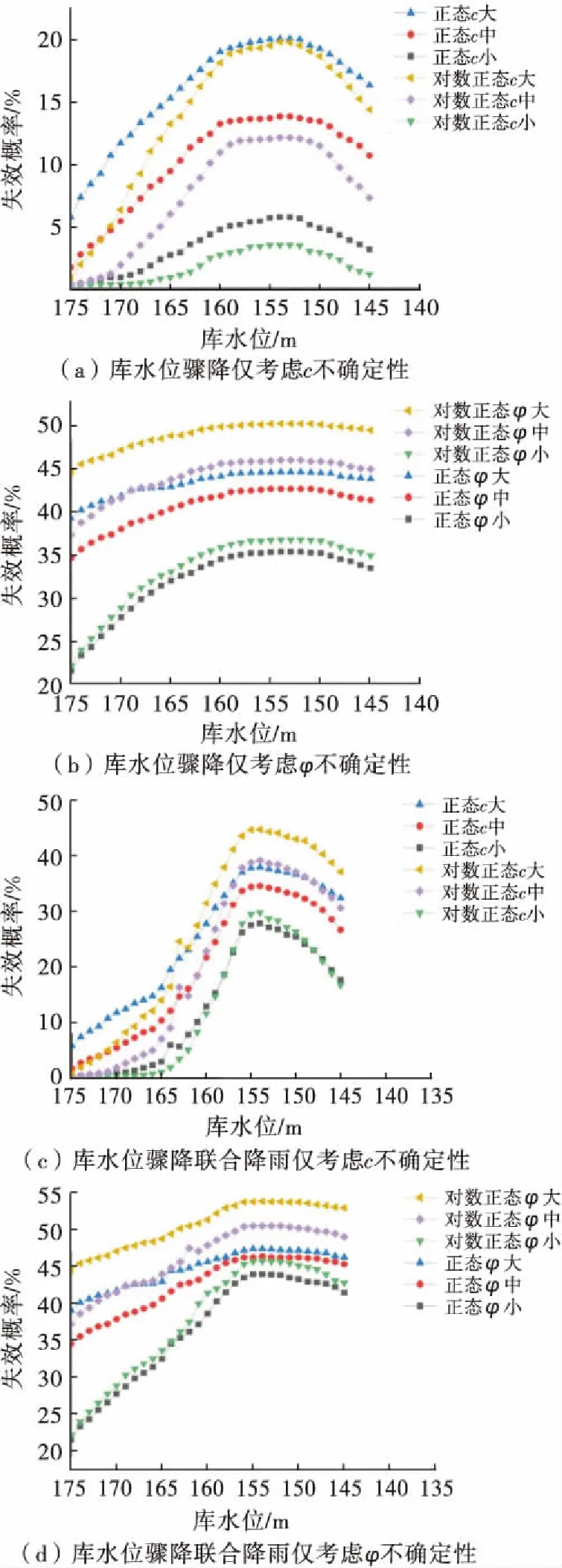
图7 仅考虑c或φ不确定性时各库水位对应的瞬态失效概率变化

由图8可知，变异系数越大，边坡的安全系数分布范围越大，安全系数小于1的占比也越大，安全系数最小值也更小；同时随着较小值和较大值等极端情况的随机获取概率的增大，其组合下的不利情况概率也相应增大，因此失效概率也变大.库水位骤降联合降雨入渗下的边坡失效概率大于仅库水位骤降下的边坡失效概率，仅考虑φ不确定性时的边坡失效概率大于仅考虑c不确定性时的边坡失效概率.

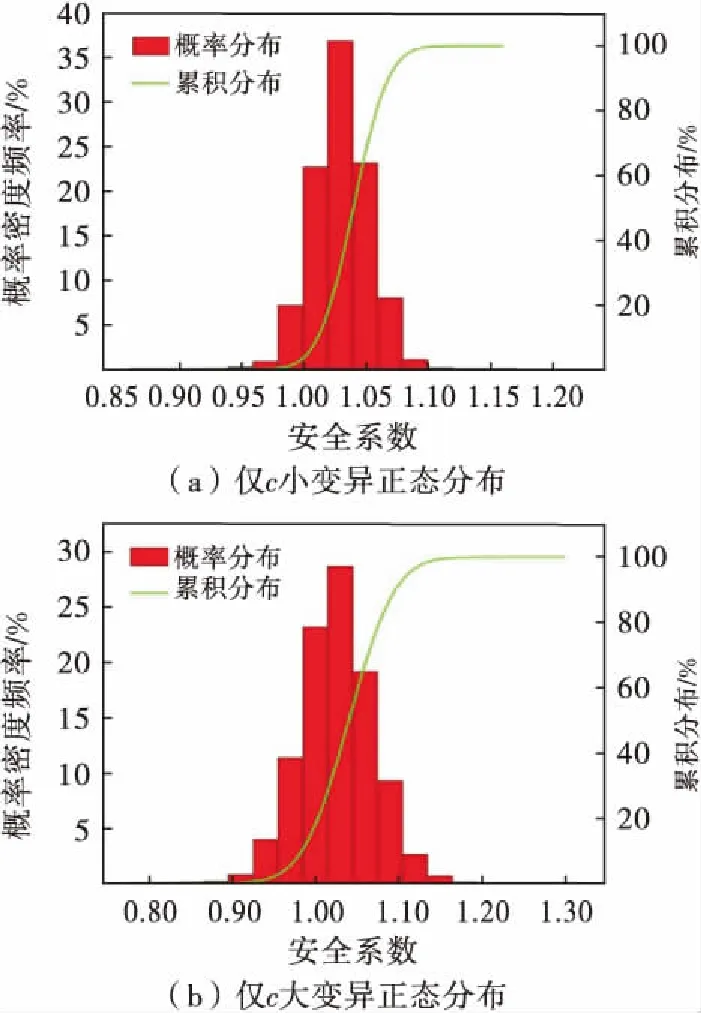
图8 库水位骤降安全系数频率直方图及累积分布函数

与此同时，库水位骤降仅考虑c不确定性时，边坡失效概率始终<30%，边坡为基本稳定状态，同一变异系数服从正态分布时的边坡失效概率始终大于服从对数正态分布时的边坡失效概率；而在此基础上叠加降雨入渗作用后，库水位降至155 m左右时边坡变为欠稳定状态，且对数正态分布下的边坡失效概率逐渐超过了服从正态分布下的边坡失效概率；仅考虑φ不确定性时，在库水位从167 m降至145 m期间边坡失效概率都超过了30%，为欠稳定状态，而在前面确定性分析仅库水位骤降工况中，边坡仅在库水位降至155 m左右时为欠稳定状态，这说明，仅通过确定性分析不能全面反映边坡稳定性状态；同时，在仅库水位骤降以及库水位骤降联合降雨作用下的边坡失效概率则始终表现为同一变异系数服从对数正态分布下的边坡失效概率大于服从正态分布下的边坡失效概率；这说明，仅考虑c不确定性时，降雨入渗作用对服从对数正态分布下的边坡失效概率的影响更为显著，边坡失效概率增长幅度更大.

4.2 同时考虑c、φ不确定性时失效概率变化

如图9所示，同时考虑c、φ不确定性时，库水位由167 m降至145 m期间边坡失效概率均>30%，为欠稳定状态；不同工况下的边坡失效概率图形变化规律大致集中分布在4个区域，库水位骤降叠加降雨入渗后边坡失效概率有小幅度的增大；当φ的变异系数相同而c的变异系数不同时，边坡失效概率变化几乎相同.

图9 同时考虑c、φ不确定性时各库水位对应的瞬态失效概率变化

对比图6可知，同时考虑c、φ不确定性时的边坡失效概率变化与仅考虑φ不确定性时的边坡失效概率变化也十分接近；这说明，同时考虑c、φ不确定性时，φ的不确定性在二者中占了主导地位，决定了边坡失效概率的变化规律.

此外，当φ的变异系数为小变异水平时，服从对数正态分布和服从正态分布下的边坡失效概率相差无几；而当φ的变异系数为中变异水平或大变异水平时，服从对数正态分布下的边坡失效概率明显大于服从正态分布下的边坡失效概率，其中φ的变异系数为大变异水平时，服从两种概率分布形式下的边坡失效概率相差最大.

5 结 论

1)随着库水位骤降，孔压总体上均有所下降，且降速越大孔压下降幅度越大；同时，上部和中部监测点孔压变化存在“响应滞后”现象，其中距离库水较远的上部滞后最明显；库水位骤降叠加降雨后，上部和中部监测点孔压在降雨的开始和结束时分别出现了“陡增”和“陡降”现象，下部监测点孔压则受降雨作用的影响较小.

2)库水位骤降及库水位骤降叠加降雨入渗下，边坡安全系数整体上均呈现先减小后增大的趋势；同时，库水位骤降速率越大，边坡最小安全系数越小，而降雨发生在库水位骤降中的10～20 d时边坡最小安全系数最小.

3)随着库水位骤降以及降雨入渗，边坡在各库水位下的瞬态失效概率均呈现先增大后减小的趋势.其它情况相同时，c、φ的变异系数越大，失效概率越大，可靠度指标越小；仅考虑φ不确定性时的边坡失效概率大于仅考虑c不确定性时的边坡失效概率，且同时考虑c、φ不确定性时，φ的不确定性占主导地位；降雨入渗作用对服从对数正态分布下的边坡失效概率的影响更为显著.

4)当边坡土体的c、φ变异系数较大时，建议假定c、φ服从对数正态分布，得到的边坡失效概率较大，结果偏安全.研究成果对进一步完善涉水边坡的可靠度研究工作有积极的促进作用.