HTPB推进剂装药蠕变行为及影响因素
王 鑫,赵汝岩,卢洪义,刘 磊,伍 鹏
(1.中国人民解放军91851部队,辽宁 葫芦岛 125000;2.海军航空大学,山东 烟台 264001;3.南昌航空大学,江西 南昌 330063)
引 言
固体火箭发动机在点火发射之前,一般需经历长时间的贮存阶段,对于垂直发射的导弹而言,还需经历立式贮存状态。固体推进剂作为装药的主要材料,由于其黏弹特性,性能会随着时间和环境发生变化,进而导致松弛和蠕变等特殊行为。基于此,长时间的定负载作用下,固体推进剂装药会产生蠕变行为,积累蠕变损伤,严重时将使装药构型发生变化,影响内弹道性能,对于体积大、质量高且需经历立式贮存的发动机而言,蠕变现象将更加明显[1-3]。因此,自重载荷作用下发动机装药的蠕变行为及影响因素研究显得尤为重要。
国内外研究者针对不同种类推进剂蠕变特性展开了相关研究,Bihari[4]采用Kelvin-Voigt模型对HTPB推进剂黏弹性进行了研究,利用动态力学分析仪记录蠕变过程,建立蠕变数学关系式。Khokhlov[5]研究了黏弹塑性材料的非线性Maxwell本构关系,可用于材料耗散、松弛及蠕变等多种现象的定性模拟。李冬等[6]利用-10~50℃范围内4种应力水平下的蠕变试验,研究了某双基固体推进剂的非线性蠕变特性。Zhang等[7-8]开展了20℃和50℃下双基推进剂的蠕变实验,并采用不同模型进行了验证。王鸿丽等[9-10]为描述材料的力学性能,利用一系列改性双基推进剂蠕变—回复试验和定加载率—回复试验结果,相继推导了黏弹性—黏塑性和黏弹性—黏塑性—黏损伤本构模型,且后者预测能力明显提高。胡义文等[11]开展PBT基复合固体推进剂的高温蠕变特性研究,证实蠕变性能与应力和温度的强烈相关性。但上述研究仅限在推进剂范围,并未对发动机装药的蠕变特性展开深入研究。
同时,研究者针对发动机立式贮存特性展开了一定的研究,王永帅[12]对某舰载固体发动机蠕变进行研究,得出了发动机装药的蠕变规律。袁军等[13]开展了大型固体发动机立式贮存状态下多种载荷联合作用下的有限元仿真及立式贮存试验,并进行了对比分析。张波等[14]开展了粘接界面疲劳强度试验和立式贮存发动机在振动载荷下的有限元仿真,计算了不同海况界面累积损伤。王鑫等[15-16]针对HTPB推进剂先后开展了蠕变试验以及交互试验,拟合了蠕变及交互损伤本构方程,并基于固化降温、重力和振动载荷作用下的数值模拟结果,获取了装药静态立式贮存的蠕变损伤和动态立式贮存的耦合损伤,但是上述文献主要集中于装药立式贮存有限元分析和损伤计算,文献[16]虽然分析了装药的蠕变行为,但未针对推进剂及发动机蠕变特性的影响因素展开系统研究。
为了研究立式贮存固体发动机装药蠕变行为及影响因素,开展接近装药实际应力水平下的推进剂试件蠕变试验,通过应变结果对比分析,验证Norton方程的有效性。分别针对卧式贮存与立式贮存两种状态开展推进剂装药长时自重载荷下的有限元分析,获取装药蠕变特性。开展不同老化时间和立式贮存次数下的蒙特卡洛随机有限元模拟,获取各参数影响蠕变结果的重要度,为发动机设计和后续的可靠性及寿命评估提供依据。
1 试验方案及模型
1.1 蠕变试验
试验对象为某型固体发动机装药所用的HTPB复合固体推进剂方坯,填充质量分数为91%,试件为哑铃型,按照QJ924-85标准制备。
文献[16]采用SDMS系列位移传感器开展了较高应力水平(0.55~0.8 MPa)下的蠕变试验,获取了特定应力范围下试件从加载至断裂全过程的应变—时间曲线,并基于Norton本构方程拟合了蠕变参数,即
(1)
式中:ε为应变;σ为等效应力;t为蠕变时间;A、m、n通过试验结果拟合得到,分别为0.028、-0.829 4和1.14。
通过初步模拟分析结果获取蠕变过程装药最大应力低于0.05 MPa,为验证该方程用于低应力水平的有效性,展开相关试验。经计算,0.05 MPa下试件断裂时间长达1010s,无法监测其蠕变完整过程;且加载应力水平较低时,较短时间内即有明显的蠕变规律体现。因此,采用MTS电子试验机进行低应力水平下的蠕变试验,从0.01~0.2 MPa中选取5个应力水平,加载方式为力保载,试验时间为3 600 s,试验在常温下进行。试验过程中实时记录并保存位移值,通过初始工程标距和位移计算实时应变,并计算各时间点的应变率。
1.2 老化试验
为开展不同贮存期的推进剂装药蠕变有限元仿真,根据航天工业部标准QJ 2328A-2005和QJ 2487-93中的规定开展相关试验。选取50、60和70℃对推进剂老化1年时间,以月为计数单位,选取8个老化时间测点取出推进剂,进行干燥后开展力学性能试验,试验温度为20℃,拉伸速率为100 mm/min,进而获取推进剂初始模量E0,推进剂的最大抗拉强度和最大延伸率变化规律见文献[17]。而后选取-20、0、20、50和70℃五个温度开展松弛试验,初始应变为5%,松弛时间为1 000 s,最后利用式(2)的Prony级数形式对试验结果进行拟合,获取推进剂平衡模量E∞、E0和E∞变化规律。
(2)
式中:t为松弛时间;Ei和τi为待定系数;E∞=E(t=∞),定义为推进剂平衡模量;E0=E(t=0),定义为推进剂初始模量。
1.3 仿真模型
所选模型为某型具有三维对称结构的固体火箭发动机,该发动机在发射之前经历长时反复的卧式与立式交替贮存。综合考虑温差、重力和充气内压载荷的作用,基于结构与载荷的对称性,发动机卧式存放时选用全尺寸结构模型进行仿真,立式存放时选取1/16结构模型进行仿真[17]。
计算过程中,通过改变E∞建立老化与仿真之间的联系,通过调整立式贮存次数(周期为半年)来改变蠕变时间。
2 试验结果及分析
2.1 蠕变试验结果
低应力水平下应变ε和应变率ε′随时间的变化规律如图1所示。由于短期内应变率变化较快,若从0 s开始,各应力水平在1 000 s后的应变率差异不明显,因此应变率初始时间设为100 s。
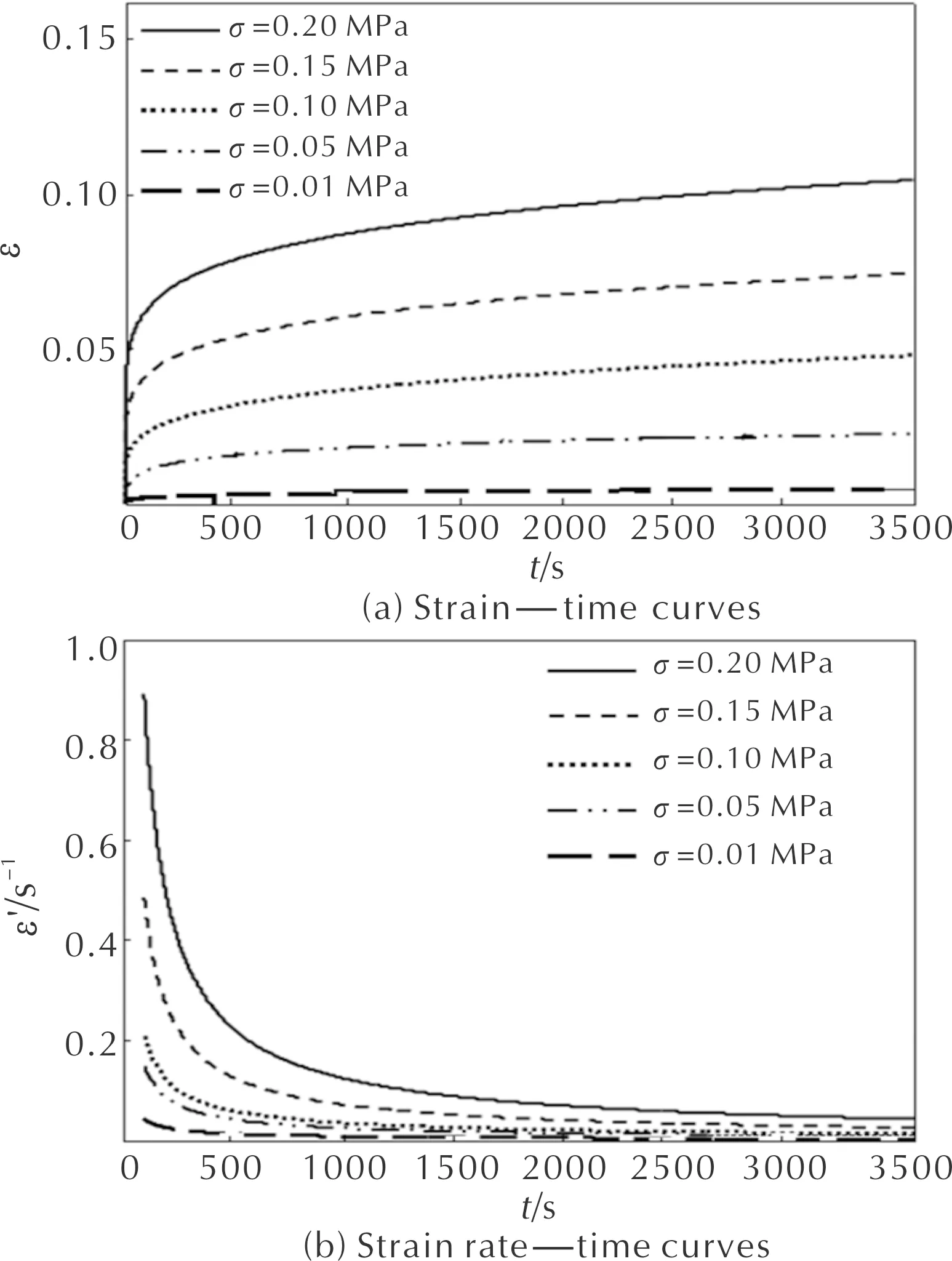
图1 低应力水平下蠕变试验的应变—时间及应变率—时间曲线Fig.1 Strain—time and strain rate—time curves of creep test at low stress level
由图1可见,各应力水平下试件应变随着蠕变时间呈增加趋势,应变率呈减小趋势;应力水平增加时,同时间段的应变和应变率也相应增加。图1(a)能较清晰地分辨出蠕变初始阶段和稳定阶段,在初始阶段,应变增加迅速,应变率急剧减小;在稳定阶段,应变缓慢增加,应变率减小缓慢。且在后续的长时蠕变过程中,应变持续缓慢增加,而应变率持续缓慢降低最后保持不变,直至进入蠕变破坏阶段。
将试验结果与式(1)的拟合结果进行对比分析,如图2所示。其中黑色线条为试验数据,红色线条为拟合数据。

图2 应变试验结果与拟合结果对比Fig.2 Comparison of strain test and fitting results
由图2可见,在3 600 s前,试验数据与拟合数据两曲线一致性较高,各点应变平均相对误差小于5%。虽然在0.2 MPa和0.15 MPa时存在一定偏差,且发动机贮存都是以年为基准,偏差随着蠕变时间逐渐增大,但在0.05 MPa和0.01 MPa时几乎完全一致,且3 600 s时应变率已接近10-8量级,后续应变变化更加缓慢,故认为方程参数可以模拟发动机蠕变规律。
2.2 老化试验结果分析
经过推进剂老化试验,获取E0和E∞的变化规律如图3所示。
由图3可见,随着老化时间的增加,推进剂初始模量和平衡模量呈线性增加,老化温度越高,模量变化越明显。根据标准QJ 2328A-2005中试验数据处理方法,采用线性方程对试验数据进行拟合,结果如表1所示。


图3 推进剂试件老化后的力学性能Fig.3 Mechanical properties of aging propellant specimens
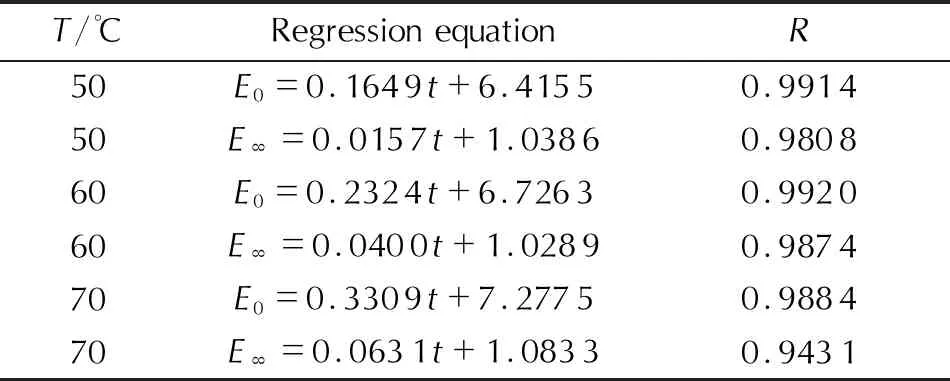
表1 各温度模量回归方程Table 1 Regression equations of modulus at different temperatures
最后推导得到常温条件下初始模量和平衡模量的关系式为:
E∞=0.002 164t+1.037
(3)
E0=0.055 98t+5.937
(4)
3 确定性有限元分析结果
3.1 卧式贮存模拟结果
从未老化发动机固化降温后经卧式存放1~10年中选取6种状态进行数值模拟,贮存10年的模拟结果如图4所示。

图4 固化降温和卧式贮存10年模拟云图Fig.4 Simulation clouds under solidification cooling and horizontal storage for 10 years
由图4(a)可见,装药在前人工脱粘层根部和前翼槽与中孔交汇处产生应力集中,贮存10年后,最大Von-Mises应力为0.023 69 MPa。由图4(b)可见,由于受壳体约束及前期热应力作用,装药前后人工脱粘结构处位移较中孔位置大,越靠近壳体,装药位移越小,药柱上下靠近中孔位置位移相差不大,最大不超过10 mm。
为清晰地看出卧式贮存状态下装药应力σ、应变ε及位移U随着贮存时间的变化,将不同贮存期的计算结果列入表2中。
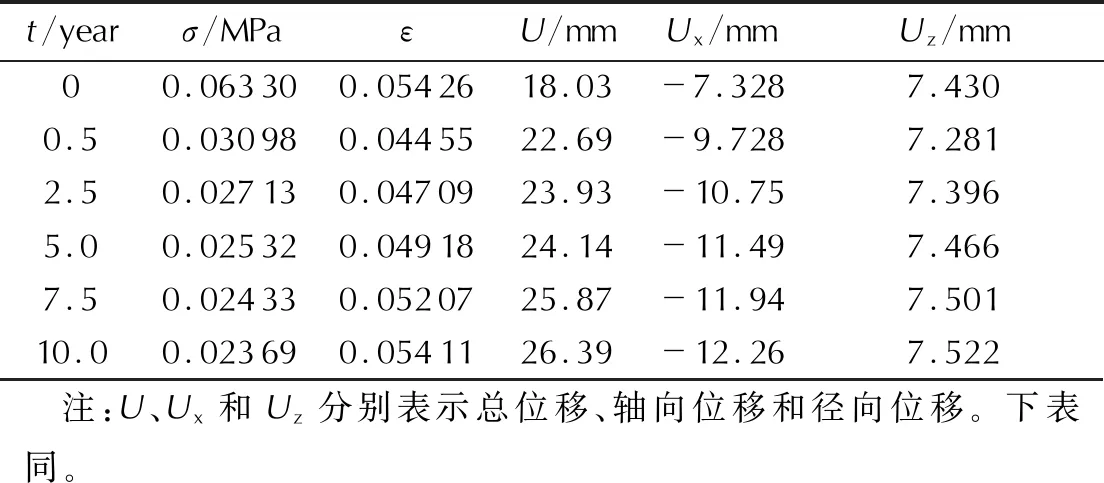
表2 装药卧式贮存不同时期仿真结果Table 2 Simulation results of grain with different periods under horizontal storage
由表2可见,随着贮存时间从0.5年增至10年,装药应力逐渐减小,应变和位移缓慢增加,增幅为20.52%和16.3%,年增长率在2%左右,且应变没有达到固化降温后的初始值。贮存10年时,总位移中仍有60%是由热应力所引起的,径向位移变化小于1 mm,轴向位移虽然增加了3~4 mm,但是其位置靠近前人工脱粘结构,对装药影响不大。
3.2 立式贮存模拟结果
3.2.1 未老化发动机蠕变结果
发动机未老化时,各参数随立式贮存次数的变化规律如表3所示。
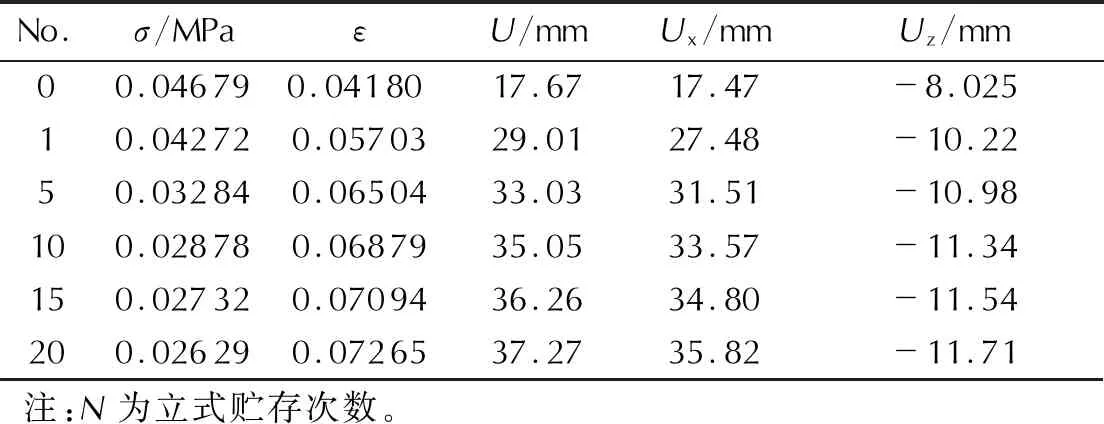
表3 未老化装药立式贮存不同时期模拟结果Table 3 Simulation results of unaged grain with different periods under vertical storage
由表3可见,随着立式贮存次数的增加,由于初始热应力较大,且蠕变所引起的应力较小,导致装药应力逐渐减小,应变和位移由于受蠕变影响逐渐增大。经过20次立式贮存后,位移和应变分别增加了110.9%和73.8%,相比于卧式贮存,发动机立式贮存状态下的蠕变效应更应引起重视。
未老化发动机立式贮存5次后的应力和位移云图如图5所示。

图5 固化降温和立式贮存模拟云图Fig.5 Simulation clouds of solidification cooling and vertical storage
由图5可见,装药前人工脱粘层根部和前翼槽内部有明显的应力集中,随着贮存时间增加,装药逐渐向尾部下沉,且下沉量从头部至尾部依次减少。
3.2.2 老化发动机蠕变结果
发动机老化后再经立式贮存,应力、应变及位移随着老化时间和立式贮存次数的变化规律如图6所示。

图6 模拟变量随老化时间和立式贮存次数的变化Fig.6 Variation of simulation variables with aging times and vertical storage times
由图6可见,同等老化时间下,随着立式贮存次数的增加,装药位移和应变逐渐增加,应力逐渐减小,且变化率逐渐减小,整体规律与发动机未老化时一致;老化时间从0年增至20年时,发动机贮存20次对应的应力、应变和位移的增减幅度分别从43.8%、73.8%和110.9%变化至60.8%、87.8%和106.7%,考虑老化因素后,应力和应变进一步增加38.8%和19%,位移变化不足4%,说明老化加速了装药的应力和应变变化,并将持续影响后续点火发射过程,但由于老化使推进剂模量变大,推进剂变硬,故位移受老化因素影响较小。
同时,随着贮存时间增加,推进剂延伸率逐渐降低,蠕变应变逐渐增加,可能诱发后期点火过程危险点应变增加,进而促使推进剂延伸率与点火应变越来越接近,导致装药寿命降低。同时,装药随着贮存时间的增加趋于定应力负载,根据线性损伤理论,其蠕变损伤会随着时间线性增加。
4 随机有限元分析
4.1 计算方法及结果分析
选取推进剂模量E、泊松比v、蠕变参数A、m、n等材料参数和温差T、充气内压p等7个变量作为随机变量,忽略其他部组件的材料属性及发动机结构尺寸变化。由于实际研制、使用以及各试验环节难以获取发动机所受载荷及材料属性的大量样本,概率模型获取较为困难。而正态模型可以描述大多数不确定参数的分布规律,本研究也将各随机变量看作正态分布,抽样方法选择蒙特卡洛拉丁超立方抽样[18],各变量变异系数分别取0.01、0.003、0.03、0.01、0.01、0.06和0.06[19]。
老化5年立式贮存1次时装药应力、应变和位移的计算结果如图7所示。

图7 老化5年发动机立式贮存1次随机有限元计算结果Fig.7 Stochastic finite element calculated results of motor aging for 5 years and vertical storage once
由图7可见,100次抽样下的计算结果服从正态分布。选取几种工况为例,列出随机有限元分析计算均值与确定性有限元分析计算结果,如表4所示。

表4 随机有限元与确定有限元模拟结果对比Table 4 Comparison of simulation results between stochastic finite element and deterministic finite element methods
由表4可见,相对误差随着立式贮存次数的增加而增加,经计算,平均值在5%以内。结合前期的正态分布检验结果,认为100次抽样可以进行装药蠕变结果的随机模拟。
4.2 蠕变影响因素分析
根据随机有限元分析结果,发动机经立式贮存后,应力和应变远达不到推进剂最大抗拉强度和最大延伸率,说明装药在贮存期间不会发生结构性破坏,但蠕变所引起发动机药型变化和积累的蠕变损伤不可忽视,应关注导致蠕变行为的主要因素。
以老化5年发动机立式贮存1次为例,列出各参数的重要度η,如图8所示。

图8 老化5年发动机立式贮存1次灵敏度分析结果Fig.8 Sensitivity analysis results of motor aging for 5 years and vertical storage once


图9 各参数的变化规律Fig.9 The variation of the importance of all parameters
由图9可见,随着t和老化后N的变化,各参数的重要度不断变化。对参数m而言,由于m与位移和应变呈正相关,与应力呈负相关,随着老化时间的增加,m对应力和位移的重要度降低,对应变的重要度增加,进而促进应力、位移值的减小和应变的增加,与其他参数共同引发了图6的变化结果。


5 结 论
(1)推进剂试件在接近实际立式贮存应力水平下短期内的蠕变试验结果与Norton本构方程拟合结果一致性较好,平均相对误差小于5%,Norton蠕变方程可以较好地模拟发动机蠕变行为。
(2)推进剂高温老化试验和松弛试验表明,随着贮存温度的升高和贮存时间的增加,推进剂模量逐渐增大,其初始模量和平衡模量表达式分别为E0=0.055 98t+5.937和E∞=0.002 164t+1.037。
(3)卧式贮存时,装药应力缓慢减小、应变年增长率约为2%,仅通过改变推进剂模量实现模拟中的贮存老化;经过20次立式贮存后,位移和应变分别增加了110.9%和73.8%,考虑老化因素时,应变进一步增加。
(4)抽样结果表明,装药蠕变结果满足正态分布,且与确定性有限元分析结果相对误差低于5%,但为减小误差,提高模拟结果的精度,后续仍应开展大量抽样次数下的随机有限元分析。
(5)各参数对蠕变结果的影响程度随着老化时间和立式贮存次数的变化而变化,m、E和v与蠕变结果相关性较强,m相关性始终最高。后续应有针对性地开展与相关参数有关的试验及模拟研究,且可添加其他部件、材料与载荷的随机分析。

