选择：决定到达方式的不同样态

贾敏

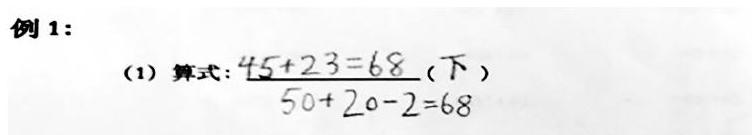
【摘 要】学生的学习过程犹如GPS导航，只要输入目的地，可以有不同的到达路径。即使过程中出现了失误，还可以重新规划新的路线再出发。相同的学习内容，学生的认识选择不同，教师的处理方式也不尽相同。而决定到达方式的不同路径，主要取决于当下的选择。不同的选择会有不同的学习过程，不同的数学思考，不同的体验与收获。这样的数学学习才是生动的、丰富的、生长的。

【关键词】数学 学习 教学 选择

（一）

笔者在执教苏教版数学二年级下册“两位数加两位数口算”一课时，让学生研究45+23和45+28两道算式。

大部分学生的算法如下。算法①：先算5+3=8，再算40+20=60，最后算8+60=68。算法②：先算5+3=8，再算4+2=6，合起来是68。算法③：先算45+20=65，65+3=68。算法④：先算40+23=63，63+5=68。

比较小结：先对加数进行分解，再将稍难的口算转化成之前学习过的比较简单的口算。

这时（如下图）学生1说：“我把45凑成50，先把23个位上的3给45，还剩20，再从20里面拿走2个。这样就算出来是68。”

多数学生满脸迷茫，教师问：“听懂他说的方法了吗？他用了以前学过的什么？”“凑十法。”学生感叹：“还能这么算！”接下来部分学生受启发有了新想法。

（二）

“解决问题的策略——假设”一课上，小组汇报交流环节，学生出现了不同的想法。或画图，或列式，或方程，解释得头头是道。

提问：“还有不同的想法吗？”学生2犹豫举手，表达了她的想法。

表格一出现，同学们齐说：“这是凑数！”

教师示意安静，听她说完。

学生2：“我用的是列表的方法。先把小杯的容量当作10毫升，小杯的容量是大杯的三分之一，大杯是30毫升，6小杯和1大杯的总量是60+30=90，不等于720毫升。再把小杯当作20毫升，大杯是60毫升，6个小杯和1个大杯的总量是6×20+60=180，不是720毫升。这样一直找下去，发现80和240正确。”

“听出什么了？”“用到假设了吗？”“如果用了假设，是怎样假设的？”

（三）

执教苏教版数学四年级下册“平移和旋转”一课时出示了一道练习：右面的这个图案可以通过平移得到吗？对于这个问题学生的认识产生了分歧，教师让学生展示、讨论、交流、质疑、反驳。

A组：我们可以先把每个圆标上序号（图2）。把上边的三个圆看作一个整体，在平移前拆分开三个圆分别平移得到左边的图（图1）。

（B组认为对，并鼓掌）

师：好像有道理，真的可以吗？

C组反驳：平移前的图案看成三个部分，可以分别进行平移。平移后，图形的形状和大小没有发生变化，只有位置发生了变化。假如这样，许多通过旋转得到的图案就可以通过“这样的平移”得到，那还学旋转做什么呢？所以我们认为A组不对，虽然三个圆平移的方向是一致的，但是平移的距离却不一样呀！

师：有道理，部分要素运动和整体运动距离不一致，图就不是原来那个图了。

一、允许不同想法的差异，寻求共同认可的思考

数学课堂上，一些同学有想法，交流了，但并不意味着所有学生都认同了，理解了。某些学生可能还有其他的想法。这些想法的背后，可能隐藏着对这个问题的其他认识。口算两位数加两位数时，学生1观察了数字的特点，有了别样“凑十”的思考。虽然也是对加数进行分解，但是他分解的思路还是有别于其他学生的。这种方法的出现打开了其他学生的計算思路，让我们不禁感叹：“还能这么算！”凑十的思维是一年级学习“20以内进位加法”的基本思维方式，学生1的介绍让我们有了耳目一新的感觉。“假设”一课中学生2有新想法，之所以犹豫，是因为自己感觉答案正确，又不太确定。更是因为大家觉得她用的不是假设，是“凑”出来的答案。是不是假设，学生2内心有想弄明白道理的愿望，表面又显得不够自信。

“学”是什么？学就是解惑，解答内心的疑惑及别人的疑惑。抓住关键条件720毫升和小杯的容量是大杯的1 —3。学生呈现六种不同的假设思考方法和解题过程，假设的方法在学生心中一点点生根，慢慢得到了大家的认同。这时突然出现的“凑数”，犹如一颗突然落在平静水池中的石子，激起了层层涟漪，将刚建立起的平衡打破了。学生心中的疑惑出现了：这个“凑数”的方法是假设吗？两位数加两位数时，学生顺着分解加数的思路，想出了不同的口算方法。学生1的不同方法打破了这种平衡，不仅用了数的分解，还巧妙地用到了凑十，为以后的简便计算做了铺垫。所以其他同学惊叹：“还可这样算！”这种凑十分解的方法也启发了其他同学进行深入思考，很快出现了不一样的凑十计算。学生思考、解释的过程就是解惑的过程、学习的过程。

“教”是什么？教就是将个体的想法在组际交流碰撞中，求得大家的理解认同。口算两位数加两位数时，学生1的方法一开始大家没太明白，满脸迷茫。分解转化是大家认同的，分解凑十是个人的认识。此时，多数学生的思路是加数分解再转化成以前学过的口算。教师问：“听懂他的方法了吗？他用了以前学过的什么？”这促使学生思考：原来学生1的想法不仅用到了分解，还要用到凑十。“还能这么算”的惊叹实际上是对这种新想法的认可和理解，因此才有了其他学生的新凑十法。此时，学生的思维由单一水平上升到了关联水平，进而向更高的创新水平进发。

二、直面不同选择的表象，剖析相同本质的理解

上“假设”一课时，开始大家的直观感觉学生2的方法就是“凑数”，听她解释以后，大部分同学仍然觉得是凑出来的。一开始，只是学生2一个人的思考和想法，从答案来说她的方法与前几种方法是相印证的，但感觉说不清楚，所以不太确定。此时教师不在各种方法上纠缠，而是直奔核心的问题理解：“用到假设了吗？如果假设了，是怎样假设的？”这样促使原来没朝这个方向思考的学生，突然有了新发现：“凑数”里用了假设。这样从原来个体模糊认识的“凑数”，经过接力思考解释，就成了部分人的当下认识：凑数里有假设。最后一言惊醒梦中人，得到所有人的认同：这里的凑数实际上就是用了假设。“前面方法中哪里用了假设？”进而进一步聚焦对比，剥离非本质属性干扰，让所有同学都认识到无论是画图、列式、方程还是列表，其实都用到了假设。这样从个体差异的“学”到部分认可再到集体认同的过程，所有人的认识都得到了补充和完善，是有意义的学。学习好比导航，输入目的地，你可以有不同的选择。你先到了，这很好，但说明不了什么问题，重要的是最后都到了目的地，即使中途走错了，又有什么关系，重新搜索仍然可以到达目的地。

很多时候，我们都受制于一种短板理论的思维。教学时让所有学生都按统一的教材、统一的要求齐步走，同时出发，也要求学生同时到达。“还能这么算！”提供的是长板理论！学习时，可能在一些方面有些板都短，比如语言表达、解决问题、实践欠缺。但是有一根长，就是有不一样的思考。面对这种不一样的思考，教师要给予学生展示的机会，这能带给学生光荣，带给学生荣誉，足以弥补学生在其他方面的缺陷。这样，人格在学习过程中才不会扭曲，性格成长才可能是良好的。这就有了成功的重新定义：成功是感到学得幸福、感到学得有意义、感到学习没有那么多的挫败、感到还不错。“还能这么算”是学生的感叹，有惊奇和发现;是老师的赞许，有意料之外的惊喜;是不经意推开的一扇窗，看到不一样的风景。“凑数用了假设吗？”是不同思想交流的场，让不同的想法在课堂上飞。这时的想法犹如许多金色的沙子，每一种看上去都很美，都想抓住，越是紧攥越留不住。这时学生的交流、沟通、理解、认同和选择，就像攥着的拳头慢慢舒展，让不适合自己的，不能理解认同的想法像流沙一样，顺着指缝流走，最后留下的是适合自己的能理解的想法。这样的教学，提供了不同的可能，让不同的人有不同的收获。

三、宽容不同学习的路径，检视共同目标的达成

当学生的认知出现分歧时，教师选择宽容不同学习的路径，让学生们交流、讨论、质疑、反驳。学生对平移的认知是有差异的，多数学生关注的是图案运动前后位置、形状、大小变化，很少关注到运动前后距离的要求。A组想到了“给每个圆标序号”的更简洁、更方便的符号化表达方式。他们将整体拆分成三个要素，分别平移再组合。这样的认识过程有一定的迷惑性和欺骗性：将①号、②号和③号所形成的组合图形看作一个整体。忽略了它们大小不同，易出现零散状的认识;每次提取单个圆平移易受圆的运动特殊性的限制。单个圆从一个位置到另一个位置，既可以看成是平移运动，也可以看成绕点进行的旋转运动。当把三个圆看成整体，进行旋转时，其内部要素会产生与A组同学想法一致的平移运动，只是这种运动就图形的整体而言不符合平移要求，因为每一个要素运动的距离不一致。

面对现状，教师及时引导：“好像有道理，真的可以吗？”这引起了学生自省式反思，才有了“看上去像是平移得到，还学旋转做什么呢？平移的方向一致但平移的距离不同”“运动前后距离不同导致图变形了，形状变了当然不是平移”的思考。这样的平移学习，引导了学生关注点的转移。从教师提炼“部分要素运动和整体运动距离不一致”开始，学生从关注要素本身的移动到关注平移本质——位置变化，形状、大小、距离不能变，关注点发生了质的变化。平移时，让学生在观察实际操作中感知并进行概念建構。建构学习的过程中教者不做过多约束，让学生自主探索不同的学习路径，让学生从不同角度进行思考，通过交流、碰撞、质疑和反驳，最后形成共同的比较全面的思考过程。这样的思考过程，学生实现了几度跨越：从单个要素认识向整体要素认识的跨越，从单个圆到整个图案的平移运动的认识跨越，从单一方向认识向多方向运动认识的跨越，从单一层面思考向全方位思考的跨越。经历多次思维碰撞后，学生从内部自觉改变认识上的偏差，形成了对平移概念的本质理解：平移可以是单一图形的移动，也可以是组合图形的整体移动。平移可以是水平或垂直或斜向移动，图案可以一次平移得到，也可以多次平移得到。达成共同的认知：无论是什么平移，平移前后，图形的位置发生变化，形状和大小不变，运动距离相同。

【参考文献】

[1]史宁中.基本概念与运算法则——小学数学教学中的核心问题[M].北京：高等教育出版社，2013.

[2]潘小福.小学数学教材的专业化解读[M].南京：江苏凤凰教育出版社，2017.