考虑局部作用力的内河渡船吊臂强度有限元分析

邵伟

摘 要：本文对内河渡船的吊臂强度分两种情况进行了有限元计算，发现在校核吊臂强度时，必须考虑吊臂受到的局部力的作用。最后，提出了对吊臂局部受力区域强度的加强方案。

关键词：吊臂强度;有限元;局部受力

中图分类号：U653        文献标识码：A            文章編号：1006—7973（2021）04-0092-03

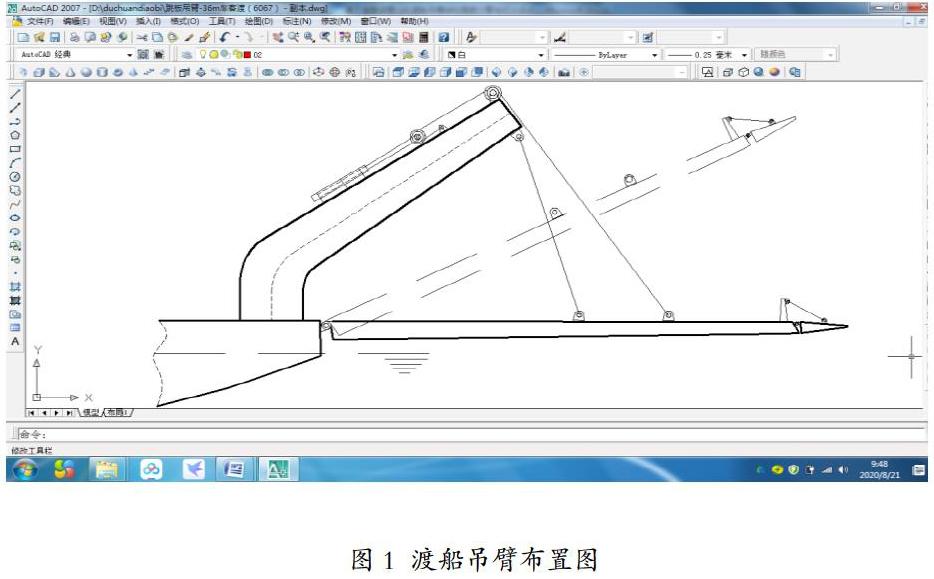
随着经济的不断发展，人们对出行的要求越来越高。在未架设桥梁的的河流上利用汽车渡船载运汽车成为很多地方的首选。相较架设桥梁，汽车渡船具有成本低、见效快的优势。汽车渡船一般设有供汽车驶入渡船甲板的跳板。在航行过程中，为防止甲板上浪以及保护汽车和乘客的目的，一般用吊臂将跳板收起，航行至渡口后，再使用吊臂将跳板降落以供汽车和乘客上下渡船。

跳板一般为重达数吨的钢质结构，因此吊臂的结构强度至关重要。《钢质内河船舶建造规范》（2016）第1篇第11章对吊臂的剖面尺寸做出了明确的规定：吊臂的结构强度可按直接计算或按梁理论计算的规定来校核。

1研究对象

本文以某渡船的吊臂为例，按照直接计算方法对吊臂强度进行计算分析。该吊臂设有液压升降系统，其中液压杆通过钢索连接动滑轮，动滑轮又通过钢索连接跳板。工作时，液压泵驱动液压油使液压杆进出液压缸，从而带动动滑轮，进而升降跳板。其中跳板自重23t。

2受力分析

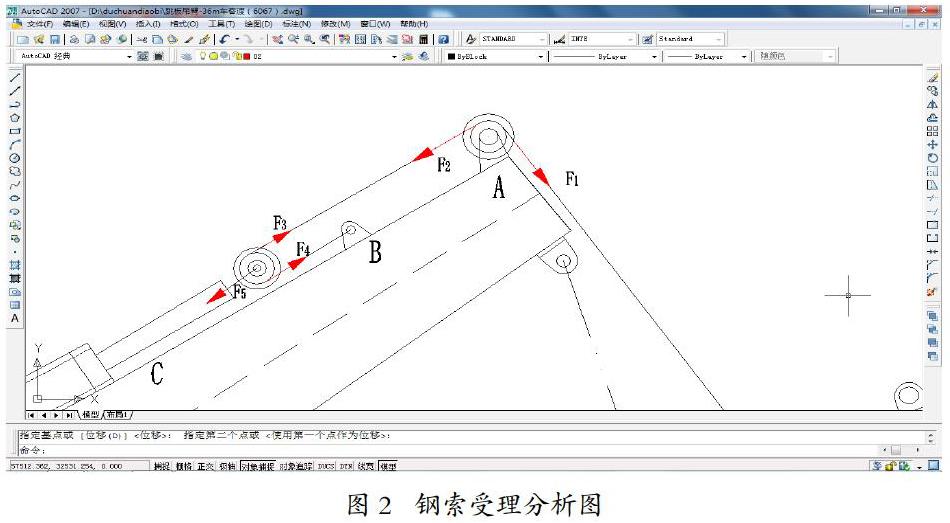
吊臂主要承受钢索的拉力，因此以钢索为受力分析对象。受力分析如图2所示。

在图2中，F1拉动跳板使其绕铰链（跳板与甲板通过铰链连接）转动。F1、F2、F3、F4为同一钢索上的拉力，因此F1=F2=F3=F4;液压杆通过动滑轮升降跳板，因此F5=F3+F4=2F1。因跳板左右对称，且左右舷对称设置一个吊臂，因此按照跳板重量的一半（G/2）进行分析。跳板绕渡船端部的铰链转动，对铰链的销钉中心取转矩，则*L1+*L2=0，其中L1为钢索与吊臂的连接点距铰链的垂直距离，L2为跳板重心与铰链的垂直距离。根据理论力学[1]，当力与转轴相交或力与转轴平行时，力对该转轴的矩等于0。计算得F1=92684.75N。根据《船舶与海上设施起重设备规范》（2007），取1.1倍的安全系数，则F=1.1F1=101953N。

3有限元计算

3.1 吊臂有限元模型

在图2中，A处的滑轮受F1和F2作用，B处的眼板受F4的作用，C处的液压筒支座受F5的作用。整个吊臂受钢索的作用力为F1、F2、F4、F5，如果不考虑A、B、C处的局部作用力（F2和F4相加之和与F5抵消），那么钢索对吊臂的作用力只有F1。本文分两种工况对吊臂的强度进行分析，工况1是只考虑F1对吊臂的作用力，不考虑A、B、C处的局部作用力;工况2考虑F1、F2、F4、F5对吊臂的作用力。

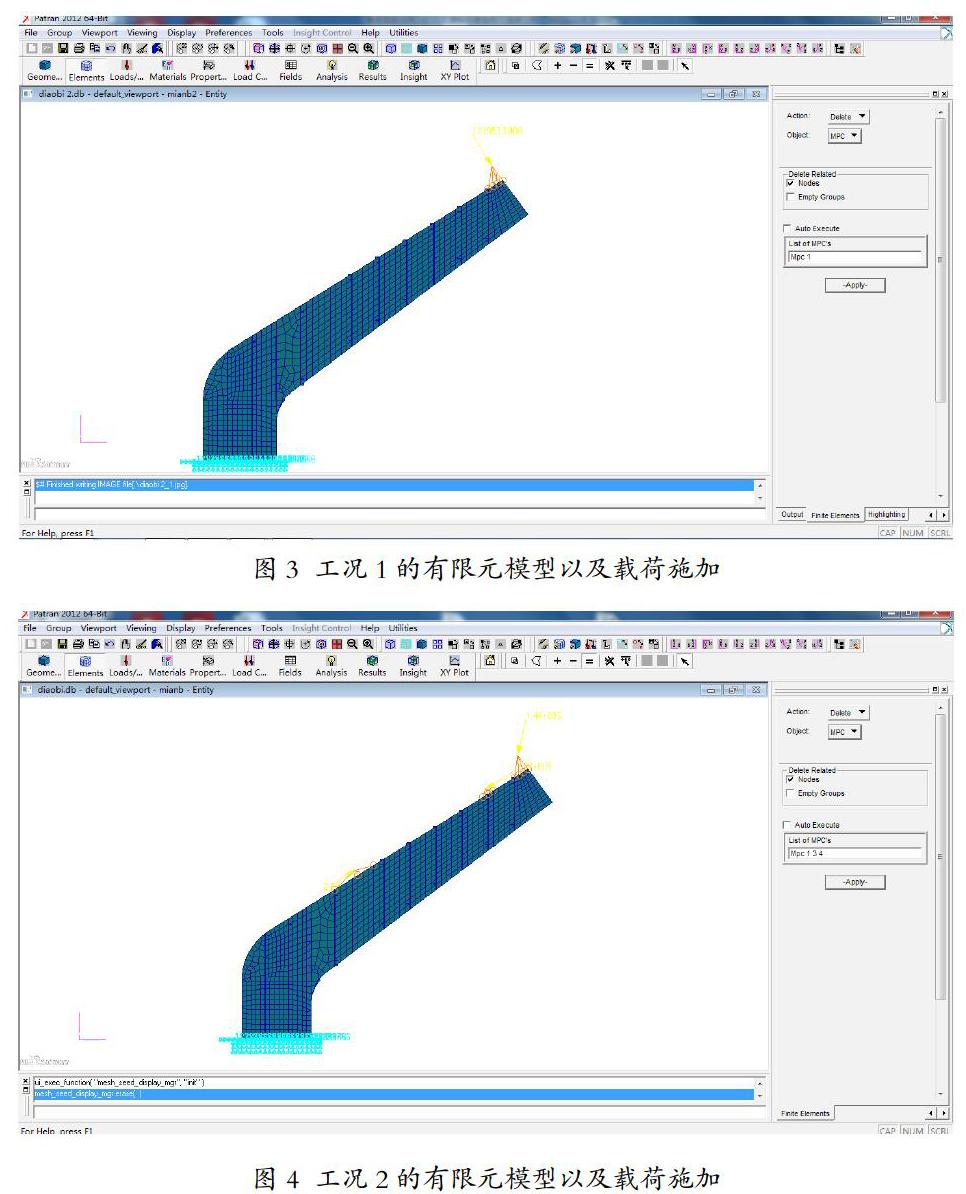
本船在船尾设两个对称布置的吊臂，因此仅建立一个吊臂的有限元模型。该模型包含3695个单元，3179个节点，坐标原点取吊臂与甲板接触区域的中心位置，吊臂纵向为X轴方向，吊臂横向（船宽方向）为Y轴，吊臂背离甲板的方向为Z轴。吊臂受到的力以MPC方式施加到相应的单元节点上。吊臂有限元模型和施加的载荷如图3和图4所示。

3.2 计算结果分析

经过计算后，工况1的最大应力为115N/mm2，满足规范要求（规范要求得许用应力衡准为135N/mm2），最大应力出现在吊臂弯曲区域，具体见图5;工况2的最大应力为157 N/mm2，明显大于许用应力衡准，最大应力出现在B处眼板区域，具体见图6。

规范只对吊臂的壁厚有明确的要求，但是对吊臂内部骨架的结构及尺寸却没有明确要求。规范同时规定对于吊臂的强度校核可采用直接计算或采用梁理论的规定进行校核。如果采用梁理论计算吊臂的强度，则假定吊臂为一端固定的悬臂梁，并承受由跳板产生的拉力。这种方法考虑的载荷和工况1采用的载荷一致，都不考虑局部力对吊臂局部区域强度的影响。虽然在整体上吊臂只承受F1的作用力，但在A、B、C处的应力是F1、F2、F4、F5对吊臂产生的应力叠加的结果。

如果不考虑局部力的作用，该吊臂的结构强度满足规范要求。而考虑局部力的作用后，则该吊臂的结构强度不满足规范要求的许用应力衡准。因此必须考虑局部力作用区域的结构加强或对该处的结构重新设计，才能确保吊臂的强度满足要求。

方案a：尽可能避免在吊臂上产生局部力。可以在A处直接设一小型的电动卷扬机来收放跳板。这样整个吊臂只承受F1的作用，无论采用直接计算还是梁理论计算吊臂的强度都不用考虑局部力的影响。工况1的模型和计算结果就是对应的方案1。

方案b：对承受局部力的区域进行结构加强。本方案在眼板下面设置沿吊臂方向的加强结构，长约0.6m的角钢（L100×63×8，和吊臂内部横框架结构的尺寸一致）。采用该方案后，局部受力区域的应力明显降低，而且最大应力的位置也发生了变化，整个吊臂的应力状态和工况1类似。

方案a和方案b的最终应力大小和分布基本一致。对于方案a，匹配到一个起重能力强且体积小、价格便宜的电动机可能会有难度;对于方案b，只要在设计的时候对局部受力区域进行相应的结构加强，就可以保证吊臂具有足够的强度。方案b较方案a有较大的可取性。

4结论

（1）对吊臂强度进行直接计算时，应考虑局部区域受力的影响。

（2）规范提出对于吊臂的强度也可按照梁理论进行计算，但是根据本文的计算结果，即使使用梁理论计算吊臂强度满足要求，但是局部受力区域的强度无法保证是否满足要求。规范可要求在设计的同时使用直接计算和梁理论对吊臂强度进行计算，以保证吊臂具有足够的强度。

参考文献：

[1]哈尔滨工业大学理论力学教研室. 理论力学（Ⅰ）[M].第六版.北京：高等教育出版社，2002：76-78.