普适的基于能量的分块局域激发态聚类算法

杜嘉辉，廖 康，洪本坤，王钟烨，马 晶，李 伟，黎书华

（南京大学化学化工学院,理论与计算化学研究所,介观化学教育部重点实验室,南京210023）

利用量子化学方法计算电子激发态是研究和预测物质光化学性质的重要手段.近50年以来，提出和发展了多种激发态方法并广泛应用于中小体系的激发态计算，如含时密度泛函理论（TD-DFT）［1，2］、运动方程单双激发耦合簇（EOM-CCSD）［3，4］和完全活性空间二阶微扰理论（CASPT2）［5］等.这些方法可以较为准确地预测体系的吸收光谱和荧光光谱.然而，传统激发态方法的计算标度过高，如基于线性相应理论的含时密度泛函理论（LR-TD-DFT）的时间标度为O（N4），高精度的EOM-CCSD的时间标度为O（N6），高计算量限制了这些方法在大型体系中的应用［6］.因此，大体系的激发态计算仍然是量子化学领域的重要挑战.

为了降低大体系激发态的计算时间，提出了多种理论方法，可以分为4类.（1）半经验激发态方法，主要通过实验数据拟合或其它近似手段快速构建哈密顿矩阵元，典型的有用于激发态的间略微分重叠（Intermediate neglect of differential overlap，INDO）方法，包括Zerner’s INDO（ZINDO）［7］和INDO for eXcited states（INDO/X）［8］，简化的Tamm-Dancoff近似（Simplified Tamm-Dancoff approximation，sTDA）［9］方法等.（2）量子力学（QM）与分子力学（MM）结合的QM/MM激发态方法［10～13］，该方法将特定的激发中心区域用量子力学处理，周围环境则利用分子力场处理，通过避免整个体系的QM计算来降低计算量.尽管上述两类方法能够有效降低计算时间，但对于具有较强长程静电和极化相互作用的复杂体系，如溶剂与溶质之间存在较强相互作用的团簇［14］或分子间产生π-π堆积的分子晶体［15］等需要对较大的中心区域或模型体系使用全量子力学的激发态计算以获得更高的精度.（3）基于局域轨道的方法，通过仅考虑激发中心区域的激发来降低计算量，可以处理大体系局域激发的情形，这类方法包括局域激发近似方法（Local excitation approach，LEA）［16］、局域框架激发方法（Local framework for calculating excitation energies，LoFEx）［17］、重整化激子方法（Renormalized excitonic method，REM）［18］等.（4）基于分块的激发态方法，包括分块分子轨道方法（Fragment molecular orbital，FMO）［19］、分而治之方法（Divide-and-conquer，D&C）［20］、分块局域分子轨道方法（Fragment localized molecular orbitals，FLMO）［21］、普适的基于能量的分块方法（Generalized energy-based fragmentation，GEBF）［22］、静电嵌入的扩展化的分子碎片共轭帽方法（Electrostatically embedded generalized molecular fractionation with conjugate caps，EEGMFCC）［23］、多层的基于能量的分块方法（Multi-layer energy-based fragment，MLEBF）［24］等，这类方法将大体系的局域激发能近似表示为一系列子体系激发能的组合.已经被运用到蛋白质、分子团簇等多种体系.

2007年，我们［25］提出了用于基态计算的GEBF方法.首先将目标大体系按照一定规则切割为若干分子片段（块），并给每块加上其周围的环境块从而产生初始子体系，再根据容斥原理产生衍生子体系；为了考虑远程和静电相互作用，在子体系周围其余原子处引入全背景电荷（在同类方法中首次）；最终整个大体系的能量可以被近似表示为一系列背景电荷嵌入的子体系能量的线性组合.经过十几年的发展，GEBF方法不仅能够成功重现多种传统电子结构方法下的单点能量，还被推广到了各种大分子和凝聚相体系的结构优化、振动光谱和核磁等［22，25～31］，相关程序被包含在免费的LSQC软件中［32，33］.2016年，GEBF方法被成功推广到大体系的局域激发态能量的计算［22］.在局域激发GEBF（LE-GEBF）方法中，体系的激发中心区域（如溶液或生物体系中心区域的生色团等）被定义为活性区域，对应的块被称为“活性块”.在构建子体系时，包含活性块的子体系被定义为“活性子体系”，其余子体系为“非活性子体系”.对于前者采用激发态方法计算其激发态能量，后者仍然计算基态能量.总体系的激发态能量可表示为所有活性子体系的激发态能量与所有非活性子体系的基态能量的线性组合.LE-GEBF方法已经成功应用于团簇及荧光蛋白等体系中［22，29，31］.

尽管LE-GEBF方法可成功预测一些大体系的局域激发态能量，但是该方法在实际应用中的鲁棒性却仍待提高，对于某些多重激发态体系组合得到的激发能可能不正确.归因于每个活性子体系激发中心周围的环境不同，可能会导致相同的局域激发在每个子体系中的能级位置不同，使得在组合激发能时不易选出对应的激发态，从而难以正确地组合得到总体系的激发能.在前期的LE-GEBF方法［22］中，采用了将活性子体系的激发能按照其对应的谐振强度由大到小排序，将排序后每个活性子体系位于相同位次的激发能进行线性组合的方法.EE-GMFCC方法则是直接取每个子体系谐振强度最大的能量进行组合［23］.由于谐振强度可以在一定程度上反映激发态的特性，并且许多局域激发具有较强的谐振强度，前期的组合方式存在一定的合理性.但是，考虑到电子激发的本质是电子态之间的跃迁，涉及电子密度的转移，仅从谐振强度这个特征来判断电子激发的特性仍然不足.如果子体系中出现其它谐振强度较大但其它激发特性明显不同的激发态就可能产生错误的能量组合，导致最终的结果出现定性错误.此外，以上激发能组合方式虽然处理具有单个较强吸收峰的体系有一定的成功率，但对于含有多个局域激发特征的体系往往只能得到其中一个激发特征对应的激发态能量，无法很好地预测其它特征对应的激发态能量.

在LE-GEBF方法［22］基础上，本文提出了一种有效的算法来自动地组合激发态.该方法可以自动分析活性子体系的激发特征，通过机器学习中的基于密度的聚类算法（Density-based spatial clustering of applications with noise，DBSCAN）来组合活性子体系中的激发能.并使用新的LE-GEBF方法计算了荧光分子衍生物、溶剂中的染料分子、绿色荧光蛋白等多种复杂体系的激发态，并与传统方法进行了比较.结果表明，新算法有效地改善了LE-GEBF方法在计算局域激发态时的稳定性，并且可以在有多种激发特性的情形下仍然对每个激发态给出较好的结果，成功重现了传统方法下的激发态能量.

1 理论方法

1.1 LE-GEBF局域激发态的计算方法

在LE-GEBF方法［22］中，（1）首先将目标大体系的激发中心区域定义为活性块，将其余部分划分为多个互不重叠的块.（2）为了考虑环境对块的影响，对于每一块（称为中心块），在其周围加上与之距离（块-块之间的最近距离）在阈值ξ（ξ通常取0.3～0.4 nm）以内的块（称为环境块）构建初始子体系.（3）为了限制初始子体系的大小以降低计算量，可设置最大块参数λ，当某个中心块周围的环境块的数量超过λ-1时，只取相距最近的λ-1块作为环境块（λ一般取4～8）.如果某个初始子体系被完全包含在了另一个更大的初始子体系中，则删除该较小的子体系.（4）为了考虑更多的多体效应，如果体系中存在一些距离较近的三块项（互相距离小于1.5ξ）或两块项（距离小于2ξ），且未被包含在之前产生的初始子体系中，则可以将这些项构建为额外的初始子体系.（5）将所有初始子体系的系数均设置为1，根据容斥原理算法，产生衍生子体系及相应的系数，对子体系末端断键的部分使用氢原子进行饱和，从而总体系可以近似表示为全部子体系通过其系数的线性组合.（6）通过子体系的基态密度泛函理论（DFT）的自然布居数分析（Natural population analysis，NPA）［34，35］组合得到的自然电荷作为目标体系的背景电荷，并嵌入每个子体系中，替代原先总体系中原子的位置，得到静电嵌入的子体系.（7）将包含活性块的子体系（M个）定义为活性子体系并进行激发态TD-DFT计算，其余子体系（N个）定义为非活性子体系并进行基态DFT计算.（8）目标体系的激发态总能量（EES）可以通过组合活性子体系的激发态能量、非活性子体系的基态能量及库伦矫正项得到［22］：

1.2 LE-GEBF组合激发能的新算法

为了准确地组合激发态能量，需要将LE-GEBF中各个活性子体系中具有相似特征的激发态进行组合.整个组合算法的流程如Scheme 1所示.首先需要对所有活性子体系的所有激发态进行分析.使用了空穴-电子分析［36］来对所有的激发态进行特征分析.该方法考虑了所有的轨道跃迁对激发的贡献，有效克服了单独的跃迁轨道对往往不能够完全描述激发特征的问题，并且还能够有效考虑退激发的情形，对不同类型的激发具有较强的适应性.利用Multiwfn程序［37］对子体系的所有激发态进行空穴-电子分析并自动使用Mulliken布居［38］计算该子体系中的每个原子i对空穴（或电子）的贡献对于激发态α，设原子i对空穴的贡献值为则构造以为元素的P维向量Aα［其中P为贡献值大于阈值（取0.5%）的原子数］.由于所有P个原子对空穴的贡献值之和近似为100%，因此Aα的模近似为1.同理对于激发态β构造P维向量Aβ.则两个激发态空穴分布的差异可用余弦相似度计算：

式中：第2项为向量Aα和Aβ夹角的余弦值，因此r A体现了两个激发态的空穴在原子贡献分布上的差异.类似地，可以计算激发态电子分布的差异：

利用式（4）可以计算出所有子体系中全部激发态之间的差异程度.

再利用DBSCAN算法来找出所有子体系中具有相似特征的激发态.该算法是一种基于密度进行聚类的算法，可以有效地处理噪声，找出空间中形状不规则的簇，并且不用指定簇的数量［39］.该算法已经在理论化学其它领域取得了应用，如寻找分子动力学的介稳构象［40］以及表征超临界流体局部密度不均匀性［41］等.由于DBSCAN无需预先指定簇的数目（在激发态分类中难以提前获知），采用该算法对所有子体系的全部激发态进行聚类.首先，设定一个较小的邻域半径eps和核心点阈值n作为参数并且用DBSCAN算法进行聚类，如果其中存在某个簇，其中包含的M个元素一一对于全部M个活性子体系的激发态特征，则将其视作一个合格的簇并从所有数据点中取出并删去，否则以步长δ（一般取0.01）增加eps的值并进行新一轮聚类.重复此过程直到当前数据集为空或eps超出上限.经过上述聚类流程，得到了多个簇，其中每个簇包含全部M个活性子体系中具有最高相似度的激发态.将簇中的M个激发态对应的激发态能量代入式（1）中进行组合即可得到总体系相应特征的激发态能量.

总之，在LE-GEBF中采用了空穴-电子分析方法得到每个子体系的所有激发态对应的电子和空穴的分布情况，并计算态-态间的差异度，最后利用DBSCAN算法对具有高相似度的激发态进行聚类，最终组合得到总体系的激发能.

2 结果与讨论

使用改进的LE-GEBF方法计算多种复杂大体系的局域激发态，这些体系包括荧光染料分子的衍生物、分子团簇以及绿色荧光蛋白（Green fluorescent protein，GFP）.所有体系的传统激发态以及所有子体系的激发态计算均使用Gaussian 16程序［42］.所有体系的空穴-电子分析使用了Multiwfn-3.8程序［37］.团簇体系的动力学和半经验优化则使用xtb-6.4.0程序［43］计算得到.LE-GEBF方法是利用LSQC程序包［32，33］实现.所有体系的结构和空穴-电子分析等值面图均是利用VMD-1.9.3［44］结合Multiwfn-3.8绘制.在DBSCAN算法中，初始邻域半径eps和核心点阈值n分别设为0.01和2.在计算过程中每完成一轮聚类后会以0.01为步长增大eps，进行下一次聚类（迭代）直到数据集中没有元素或达到上限0.3为止.所有轮聚类结束后，对每个合格簇中的元素（激发能）分别组合即得到目标体系的所有局域激发能.

2.1 荧光染料分子衍生物

首先，研究了一系列具有多个局域激发特性的荧光染料小分子衍生物的吸收光谱，包括3种典型的荧光染料分子咪唑啉、香豆素以及芴的衍生物体系.每个体系均在原来的分子基础上添加长碳链而成.3个体系的基态结构如图1所示，图中红色虚框标注部分为活性中心区域（生色团）.所有体系的结构都是在ωB97XD/6-31G（d）水平下优化得到，并在TD-ωB97XD/6-31G（d）下分别使用传统方法与LE-GEBF方法计算激发态.在LE-GEBF计算中，活性中心区域作为完整的活性块，其余部分使用LSQC程序自动分块，计算中的距离阈值取0.3 nm.

识字量大，学生任务重，对识字不感兴趣，回生快，识字教学方法单一，效果不好，使识字成了学生的难点，也成了教师教学中最头疼的问题。

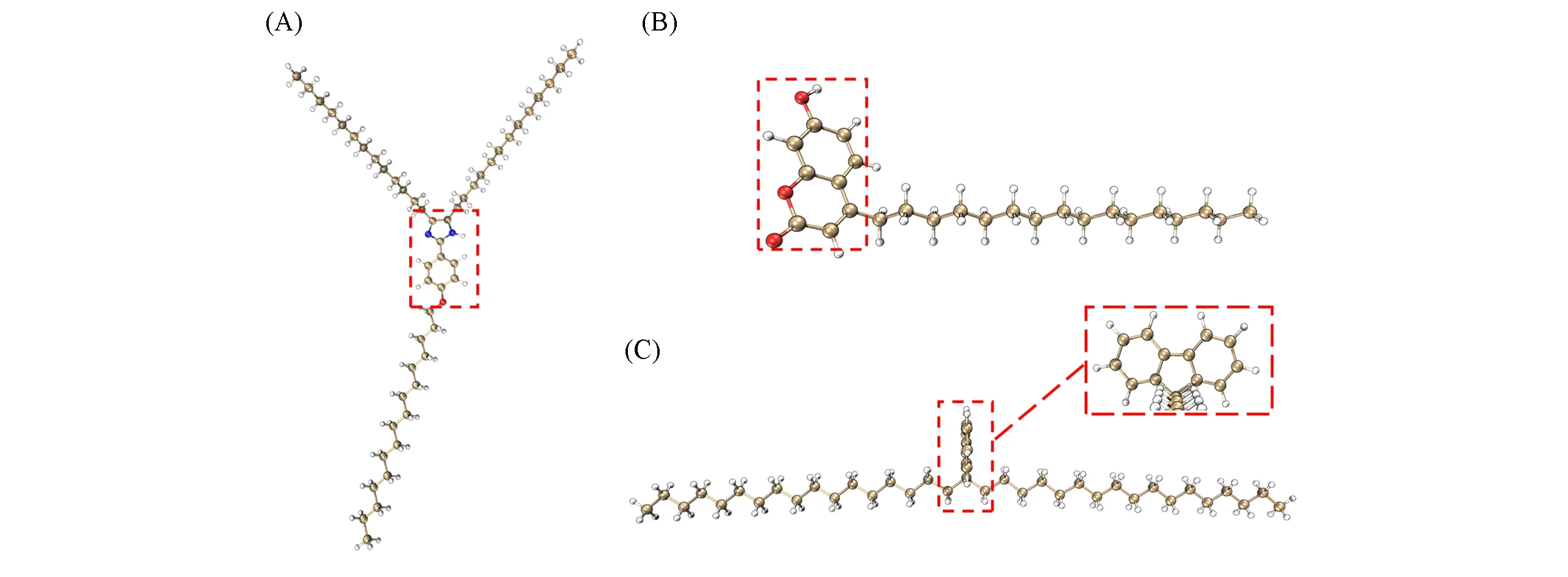
Fig.1 Derivatives of fluorescent dyes of imidazoline derivative(A),coumarin derivative(B)and fluorine derivative(C)

对于咪唑啉的衍生物，传统TD-DFT方法计算的前5个态中，所有激发态均是以体系中央的生色团为激发中心的局域激发，且所有态都存在激发特征和能量上的差异，电子-空穴分析的结果如图2所示.第一、二、四、五激发态为π→π*跃迁，且其中第二激发态存在一定的从咪唑环向苯基的电荷转移.第三激发态则是从五元环上氮原子的孤对电子到整个咪唑啉的n→π*跃迁.其计算结果与传统方法计算结果列于表1，结合了新的激发态组合算法的LE-GEBF方法成功地复现了所有不同的局域激发特征所对应的激发能.该体系中不同激发态对应的LE-GEBF与传统TD-DFT激发能的偏差均不超过0.02 eV.如对于较高的第五激发态，LE-GEBF和传统TD-DFT的激发能非常接近，分别为6.44和6.45 eV.

Fig.2 Hole-electron analyses of the first five excited states of imidazoline derivative

Table 1 Comparisons of the conventional TD-DFT and LE-GEBF-TD-DFT excitation energies(eV)of three types of fluorescent dyes

类似的，对于香豆素衍生物和芴衍生物体系，传统方法计算了每个体系的前5个态，体系的激发中心区域也均分别存在5个局域激发.两个体系所有激发态的空穴-电子分析结果分别如图3和图4所示.对于香豆素衍生物，其第一、二、四、五激发态为π→π*的跃迁，第三激发态则表现出了明显的从氧原子到整个生色团的n→π*跃迁性质.对于芴衍生物体系所有的5个激发态均表现为整体生色团上的π→π*跃迁.相应传统TD-DFT方法和LE-GEBF计算的局域激发能结果见表1，两者的误差都在0.02 eV以内.可见，改进后的LE-GEBF算法对这两个体系所有的局域激发能均能够给出很好的预测.

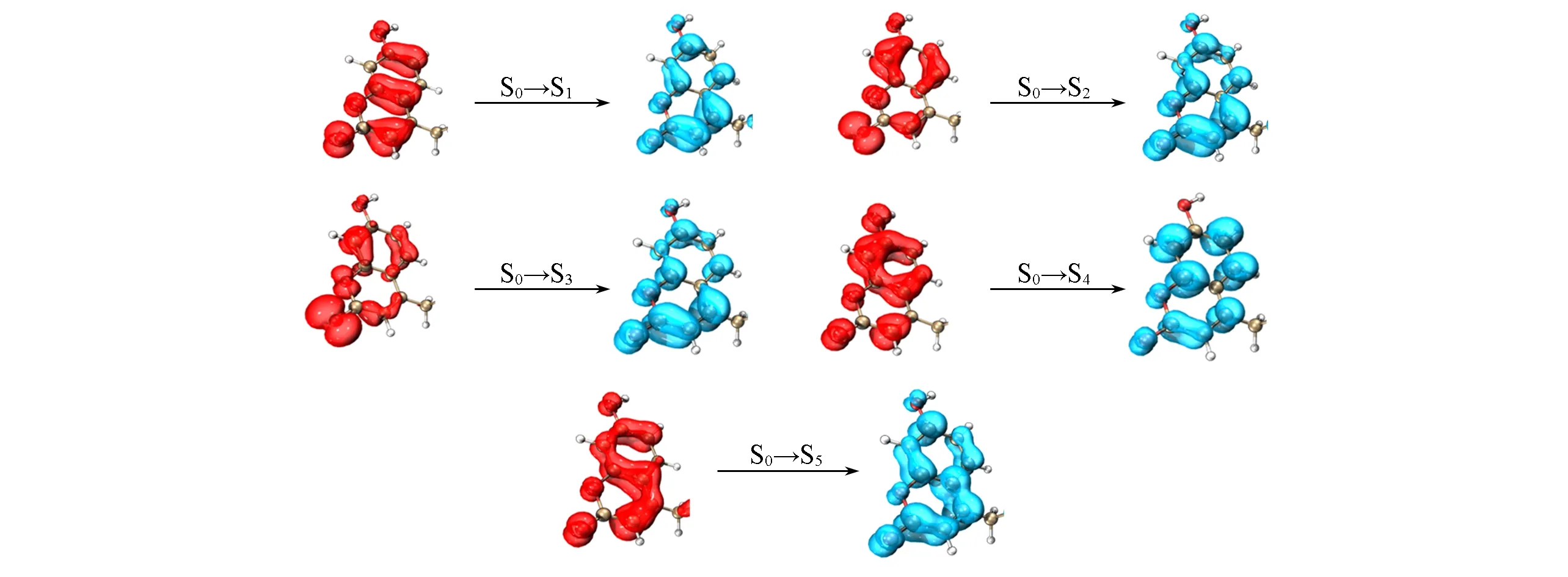
Fig.3 Hole-electron analyses of the first five excited states of coumarin derivative

Fig.4 Hole-electron analyses of the first five excited states of fluorine derivative

通过对比上述所有的计算结果不难看出，对于上述所有体系，改进了激发态组合算法后的非曲直LE-GEBF方法可以成功地复现出体系所有可能出现的局域激发能.即使体系存在两个或更多局域激发态，新的算法也可以有效地将其分别识别出来并自动进行组合得到相应的准确激发能，克服了以往的组合方案往往只能预测一个较强吸收峰的缺陷，使LE-GEBF方法可以有效处理激发中心存在多个局域激发态的体系.

2.2 分子团簇

除了以上3种模型体系，该算法的另一个潜在应用是能够更好地预测分子在溶液中的吸收光谱.在计算分子的构象平均下的吸收光谱时，往往需要计算得到体系大量构象对应的所有激发能和对应强度并进行统计平均.在计算显示溶剂模型体系的情况下，LE-GEBF方法虽然能够大大降低具有较大溶剂-溶质团簇的激发态的计算耗时，但是在之前排序方法下的LE-GEBF方法往往仅能够预测每种构象中最强的吸收峰，对于每个构象的一些较弱的峰有时需要手动挑选对应激发态进行组合，这在活性子体系较多的团簇类体系需要耗费较多时间.而新的组合算法则可以自动地寻找并组合所有子体系中相似度最高的激发态.

利用改进的LE-GEBF方法分别计算了尿嘧啶［29］、HN12分子［45］和3HAB分子［46］在水溶液中团簇的激发能.每个团簇均在取自于相应溶液的分子动力学模拟（GFNFF力场［47］）后，并在GFN2-xTB［48］下优化得到结构.优化后的团簇结构如图5所示.3个团簇均在TD-ωB97XD/6-311G（d，p）水平下分别使用传统方法和LE-GEBF方法计算了激发能，结果见表2.

Fig.5 Clusters of uracil(A),HN12(B)and 3HAB(C)in aqueous solutions

Table 2 Comparisons of the conventional TD-DFT and LE-GEBF-TD-DFT excitation energies(eV)of three clusters in aqueous solutions

首先，对比尿嘧啶-水团簇的空穴-电子分析结果，可见在该体系的前5个激发态均是位于中心尿嘧啶分子上的局域激发（图6），其中第一和第三激发态均是从氧原子到六元环上的n→π*跃迁，其余则对应于整个环上的π→π*跃迁.其激发能计算结果（表2）表明，所有5个激发均被新的算法成功找出并组合得到与传统方法相近的激发能，误差均≤0.05 eV.其中偏差最大的为第四激发态，LE-GEBF和传统TD-DFT激发能分别为6.32和6.37 eV，其余4个激发态的LE-GEBF计算偏差均≤0.03 eV.

Fig.6 Hole-electron analyses of the first five excited states of uracil-water cluster

第2个团簇为HN12分子在水中的团簇，该体系在传统方法下计算所得到的前8个激发态中共有4个态的激发中心区域位于溶质分子，空穴-电子分析如图7所示，其中S0→S2的跃迁是从氧原子到醛基上的n→π*跃迁，其它3个态均是在整个生色团上的π→π*跃迁.激发能对比结果表明，改进的LEGEBF方法也能够比较好地复现出传统方法下的局域激发能结果，最大偏差仅为0.03 eV（对应于第四个局域激发态）（表2）.

Fig.7 Hole-electron analyses of the first five excited states of HN12-water cluster

最后一个团簇为3HBA分子在水溶液中的团簇，TD-ωB97XD/6-311G（d，p）水平下计算的前5个激发态均是位于生色团上的局域激发，空穴-电子分析结果如图8所示.其中第三激发态表现为明显的从氧原子到苯基和羧基的n→π*激发，其余激发态则表现为π→π*的激发.激发能对比显示，对于该体系，改进的LE-GEBF方法仍能给出与传统方法相当的结果（表2）.其中最大偏差出现在第三激发态，相应的LE-GEBF和传统的TD-DFT激发能分别为5.95和6.00 eV.而对于最低激发态，LE-GEBF-TDDFT给出的激发能（4.67 eV）与传统结果一致.

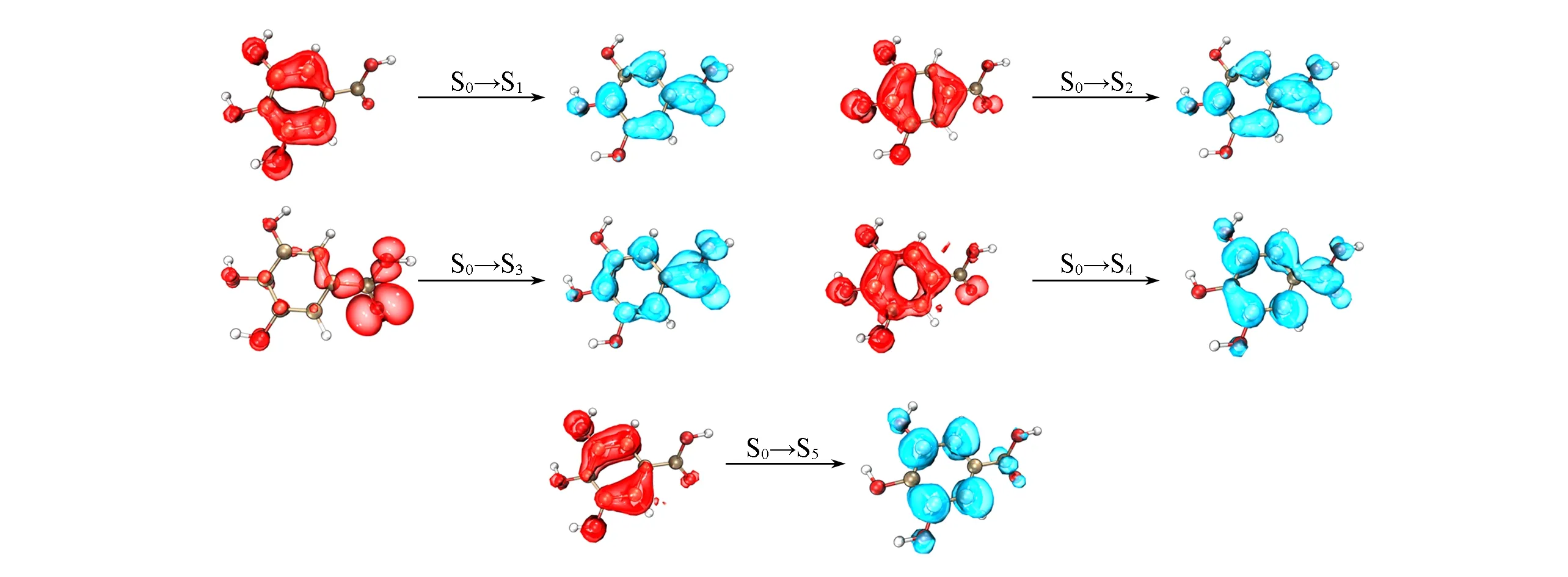
Fig.8 Hole-electron analyses of the first five excited states of 3HBA-water cluster

综上，对于溶液团簇体系，改进的LE-GEBF方法可以非常准确地复现与传统方法结果相当的激发能，且其结果对于具有多个位置和强度的吸收峰均能给出较好的结果，未来可以应用于预测如热激发延迟荧光材料（TADF）、金属杂多酸等具有多重吸收峰结构的分子在溶液中的吸收光谱.

2.3 绿色荧光蛋白

荧光蛋白是一类具有重要发光性质的生物大分子体系.其中绿色荧光蛋白（GFP）及其衍生物的研究引起了广泛关注.GFP呈β-桶状结构［图9（A）］，存在于许多发光的水生生物中［49，50］.其生色团是位于GFP结构中央的Ser65，Tyr66和Gly67 3个残基.由于其显著的生物光化学性质，GFP作为重要研究工具被广泛应用于分子生物学等领域，在基因表达及荧光成像等方面有着重要的应用价值.使用改进后的LE-GEBF方法计算了两个GFP模型体系的局域激发能.第一个模型体系结构（模型I）来自于Kaila等［51］的研究［图9（B）］，初始构型来自于PDB数据库［52］（ID：1EMB），包含了T62，Q69，Q94，R96，H148，V150，T203，S205，E222残基以及生色团和附近水分子.在LE-GEBF-TD-B3LYP/6-31G（d）水平下，计算得到其激发能为3.18 eV，与相应TD-DFT计算的激发能（3.17 eV）及实验值（3.12～3.14 eV）［50］均相符.

Fig.9 Structures of green fluorescent protein(GFP)of whole system(PDB ID:1EMB)(A),GFP model I(161 atoms)(B)and GFP model II(733 atoms)(C)

为了更好地考虑周围环境对激发的影响，还对取自相同蛋白中的更大的GFP模型体系（模型II）［图9（C）］［31］在GEBF-TD-ωB97XD/def2-TZVP水平下进行了计算.该模型体系包含生色团周围环境0.7 nm内的残基，共733个原子.该体系在其计算水平下有13204个基函数，传统TD-DFT单点激发态能量计算在常规服务器上难以实现.因此使用改进的LE-GEBF方法计算了其吸收光谱，所得结果为3.15 eV，与实验值更加接近.对于GFP模型Ⅱ体系无法进行传统的激发态计算，故对以生色团为中心的活性子体系进行空穴-电子分析（图10），结果显示，该体系的局域激发是位于五元环上的π→π*激发.因此，改进的LE-GEBF方法对于具有局域激发的较大的实际生物体系也能给出稳定并令人满意的结果.

Fig.10 Hole-electron analyses of the first excited state of a GEBF active subsystem(centered on chromophore)in GFP modelⅡ

3 结 论

在普适的基于能量的分块局域激发态计算方法框架下，利用机器学习中的聚类算法，提出了一种新的子体系激发能组合算法，可以在原有LE-GEBF方法的基础上自动地比较子体系各激发态的相似程度，并进行分类线性组合，进而得到目标体系所有可能的局域激发态的能量和相应的激发能.该方法利用空穴-电子分析的分布特征作为描述符，并利用DBSCAN密度聚类机器学习算法，在子体系中找到具有高度相似特征的激发态，克服了以往GEBF方法在计算具有多个局域激发体系时的组合困难.测试了包括荧光染料分子衍生物、染料-水团簇和绿色荧光蛋白模型在内的各种体系，激发能计算结果显示，新的组合算法可以有效地识别并分类子体系中各种不同的局域激发态并进行组合，得到目标体系局域在生色团上多个激发态能量和相应的激发能.当前的激发态聚类算法虽然已经可以自动计算多种类型大体系的吸收光谱，但尚未考虑相位因素对激发态的影响，对于一些包含高对称性生色团的体系未必能完全表征激发态的特性.此外，原子对空穴或电子部分的贡献基于Mulliken布居数分析，不适用于弥散函数的基组.需要进一步改进算法，引入相位因素并拓展至弥散基组，并实现激发态能量导数的计算，以进行激发态的结构优化、发射光谱及振动光谱预测，从而将LE-GEBF方法应用于更多复杂体系的电子光谱.