无迹卡尔曼滤波法估计锂离子电池的SOC

高博洋,刘广忱*,张建伟,王生铁

(1. 内蒙古工业大学电力学院,内蒙古 呼和浩特 010080; 2. 内蒙古自治区电能变换传输与控制重点实验室,内蒙古 呼和浩特 010080; 3. 内蒙古电子信息职业技术学院,内蒙古 呼和浩特 010070)

锂离子电池具有电压高、循环寿命长等诸多优点,但有时会出现严重事故,如过充电或过放电导致电池自燃或爆炸[1]。 荷电状态(SOC)是电池管理系统(BMS)衡量电池性能的主要因素。 准确地估计电池的SOC,不仅能防止出现过充或过放,还能降低事故的发生率。 常用的电池SOC 估算方法有开路电压法、安时积分法、神经网络法和卡尔曼滤波(KF)法等[2-3]。 对于电池这样的非线性系统,目前大多采用改进的KF 算法对SOC 进行估计[4-6]。 锂离子电池内部电化学反应比较复杂,必须建立合适的模型,将锂离子电池内部和外部工作特性联系起来[7]。 目前常用的模型主要有电化学模型、神经网络模型、耦合模型和等效电路模型等4 类。

本文作者选择二阶RC 等效电路模型,通过对电池进行大量充放电实验得到的数据,离线辨识出模型中的各个参数,利用无迹卡尔曼滤波(UKF)法和扩展卡尔曼滤波(EKF)法对电池SOC 进行估计。 通过对比仿真,验证UKF 法对锂离子电池SOC 估计的准确性和可行性。

1 模型建立和参数辨识

1.1 电池模型的选取

大量实验表明,二阶RC 等效电路模型与三阶或更高阶模型的精度差别不大,计算量相对较小,又比Thevenin 等效电路模型精度高,还很好地模拟电池不同的极化特征,因此,实验选用图1 所示的二阶RC 模型作为研究模型。

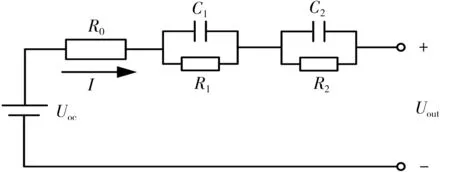
图1 二阶RC 等效电路模型Fig.1 Second-order RC equivalent circuit model

图1 中:Uoc为开路电压;R0为欧姆内阻;I为流过电阻R0的电流;Uout为端电压;C1和C2分别为两个极化电容;R1和R2分别为两个极化内阻。 得到相关的数学表达式为:

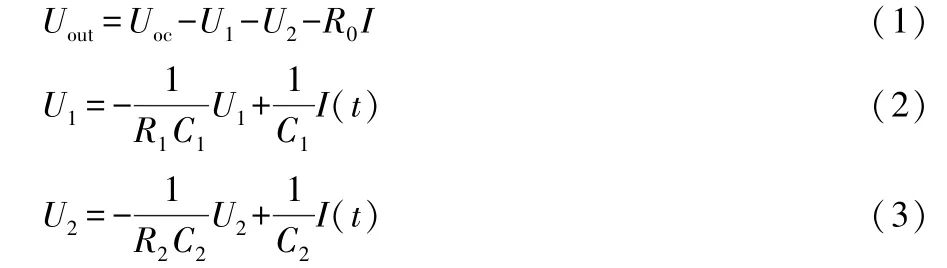
式(1)-(3)中:U1为极化回路R1C1两端的电压;U2为极化回路R2C2两端的电压;t为充放电时间。

结合安时估计法,SOC 定义如式(4)所示。

式(4)中:S0、Sts分别是初始和ts时刻的SOC 值;Qv是额定容量;ηi是库仑效率;i为ts时刻的电流。

将电池模型进行离散化处理,得到离散的状态方程和输出方程为:

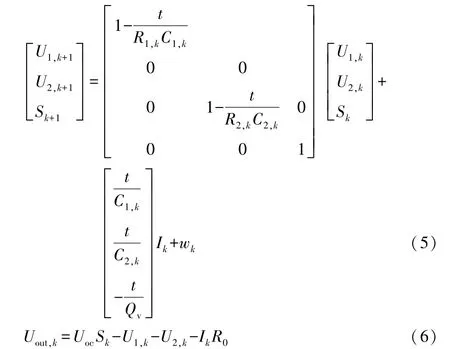
式(5)-(6)中:t为采样时间;k表示时刻;Ik为系统工作电流;wk为系统过程噪声;S为SOC 值。

1.2 电池模型参数离线辨识

二阶RC 等效电路模型需辨识的参数有:开路电压Uoc、欧姆内阻R0、极化内阻R1和R2、极化电容C1和C2等。

对满充电池进行脉冲放电,测量每次脉冲放电后的Uoc,对放电实验得到的SOC 和Uoc关系进行非线性拟合,可以辨识Uoc。 实验对象为3 只LGABC21865 型钴酸锂锂离子电池(南京产,额定容量为2.8 Ah)串联组成的电池组。 实验步骤为:在室温环境下,以1.00C(2.80 A)恒流充电至12.6 V,转恒压充电至电流小于0.05C(0.14 A),此时电池视为已充满。 以0.20C放电15 min,放出额定容量的5%,静置30 min,得到开路电压,再重复放电过程1 次,此时SOC=0.90;然后以0.20C放电30 min,静置30 min,重复此过程8 次,此时SOC=0.10;记录每次静置后的电压,最后,以0.20C放电15 min,静置30 min,此时SOC=0.05。 根据所得数据,对实验数据进行6 阶多项式拟合[8],Uoc-SOC 拟合的关系曲线如图2 所示。

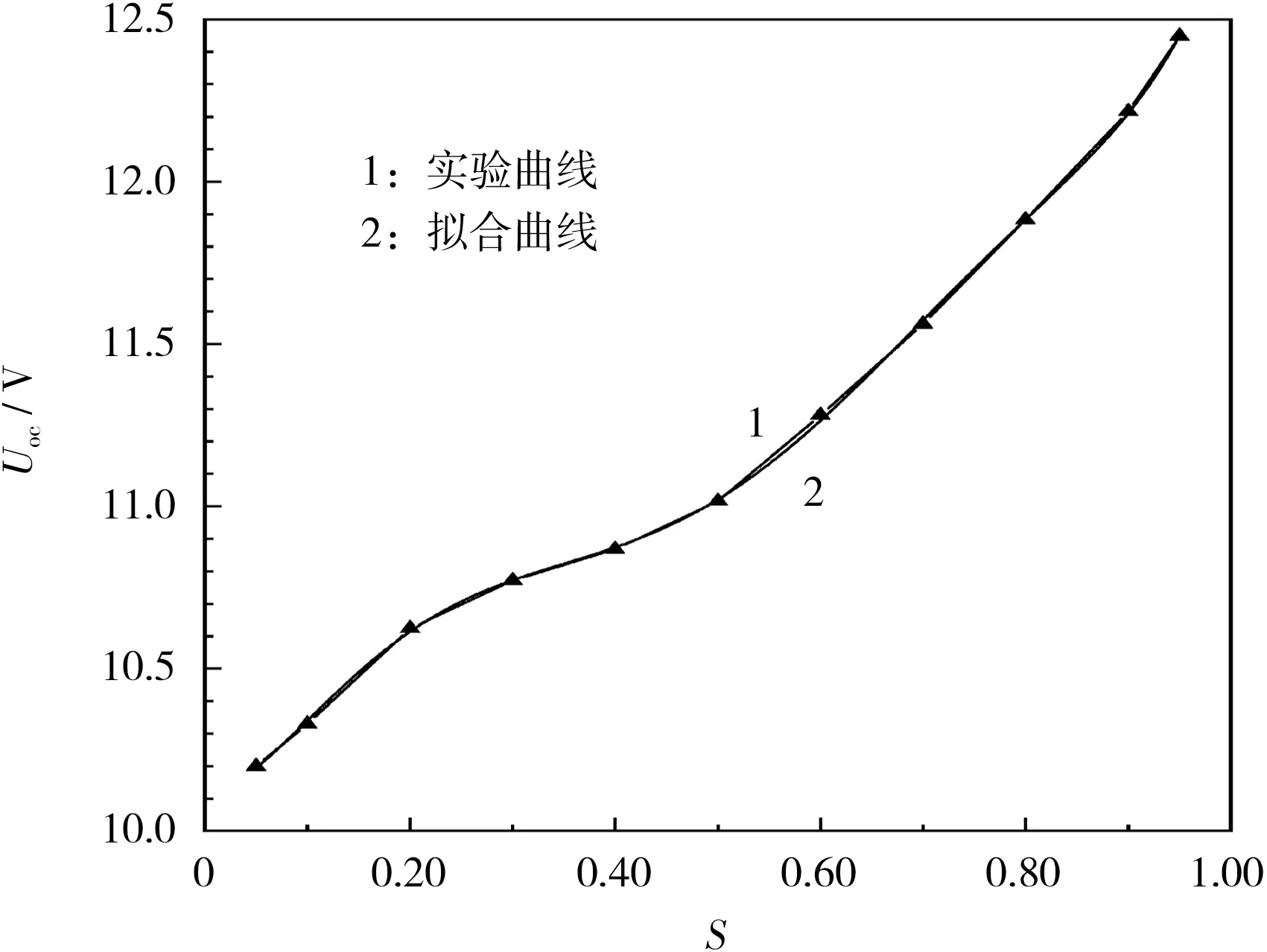
图2 Uoc 与SOC 的关系Fig.2 Relation between Uoc and SOC

从图2 可知,拟合曲线与实验曲线基本一致,说明采用6阶多项式的拟合度较高,有助于提高SOC 的估计精度。

采用脉冲放电实验来辨识模型中的其他参数,以1.00C电流放电,放电时间为3 min,电池放出额定容量(2.8 Ah)的5%,此时电池SOC=0.95,静置30 min;再重复放电过程1次,此时SOC=0.90;以1.00C放电6 min,静置30 min,重复此过程8 次,此时SOC=0.10;最后,以1.00C放电3 min,静置30 min,此时SOC=0.05。 SOC=0.80 时,脉冲放电端电压与电流的关系如图3 所示。

图3 脉冲放电电流与端电压Fig.3 Current and terminal voltage of pulse discharge

从图3 可知,电池在放电开始或放电结束的瞬间,端电压都会发生突变,此现象是由欧姆内阻R0引起的,R0的计算公式为:

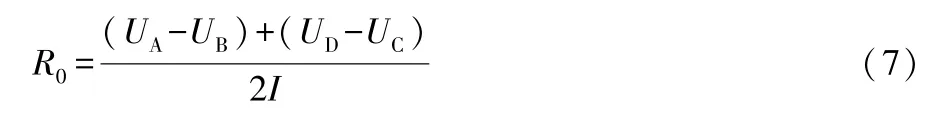
式(7)中:UA、UB、UC和UD为图3(a)中相应各点处的端电压值。

电池在脉冲放电结束后,从C 点到静置时间E 点的响应可视为电路的零输入电压响应。 利用Origin 软件对图3 中的DE 段进行二阶指数拟合,拟合曲线如图4 所示。

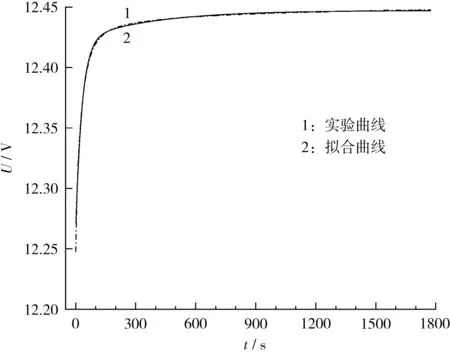
图4 DE 段端电压的拟合曲线Fig.4 Fitting curve of terminal voltage in DE section

拟合公式如式(8)所示:

式(8)中:y等效为端电压;y0等效为开路电压;A1等效为极化回路R1C1两端电压的负值;A2等效为极化回路R2C2两端电压的负值;t1、t2为极化时间常数;e 为自然常数。

根据式(8),并结合电路的零输入电压响应,得到模型的各参数值,如表1 所示。

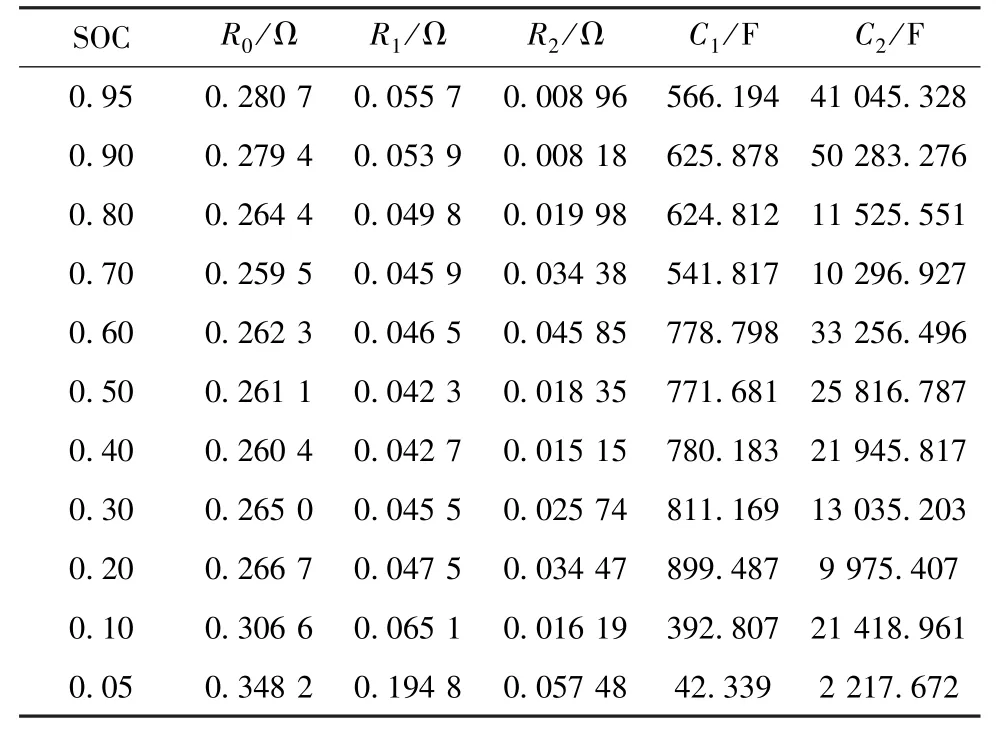
表1 电池模型参数离线辨识结果Table 1 Offline identification results of battery model parameters

1.3 模型验证

在MATLAB 中建立二阶RC 等效电路仿真模型,根据得到的模型参数及实验得到的电压和电流数据,验证离线辨识模型参数的准确性。 仿真验证结果如图5 所示。

图5 脉冲放电仿真结果Fig.5 Simulation results of pulse discharge

从图5 可知,测量电压与仿真电压曲线在17 040 s 之前基本吻合,但之后两者的差别较大;同样,从误差曲线可知,在17 040 s 前,误差(E)在[-0.04 V,0.04 V]区间内上下波动,说明在此区间内测量值与仿真值差别很小;在17 040 s后,测量值与仿真值差距急剧增大,主要原因是:当电池放电到截止电压附近时,端电压下降速度急剧加快,且此时放出的电量很少,另外,利用安时积分法计算时,放电时间越长,误差积累越大。 从整体来看,采用离线辨识法辨识出的等效电路模型参数,能较好地模拟锂离子电池的工作特性。

2 电池SOC 估计

KF 法一般针对线性系统,对于电池这样的非线性系统不再适用,因此,实验采用EKF、UKF 法等改进的KF 法对电池SOC 进行估计。

EKF 法在计算时,首先要对非线性模型进行线性化处理,再利用KF 法完成对状态的预估。

非线性离散系统的状态空间模型方程一般为:

式(9)-(10)中:yk为k时刻的输出值;xk为k时刻的状态变量;uk为系统的控制输入变量;vk为系统观测噪声;f(xk,uk)为系统的非线性状态转移函数;g(xk,uk)为系统的非线性观测函数。

将f(xk,uk)和g(xk,uk)非线性离散系统局部线性化后,对式(5)按一阶泰勒级数展开,得到模型线性化处理后的状态转移矩阵Ak、输入矩阵Bk、输出矩阵Ck和前馈矩阵Dk:

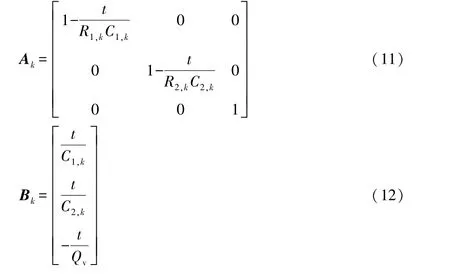
线性化处理后的离散模型为:

将模型线性化处理后,再根据KF 法的递推步骤,完成对锂离子电池SOC 的估计。

UKF 法的核心是无迹(UT)变换,UT 变换的关键是确定σ采样点个数、位置和对应的权值。

基于UT 变换及式(9)、(10)的非线性系统,UKF 法实现的具体步骤如下。

①初始化状态变量的均值x与协方差P

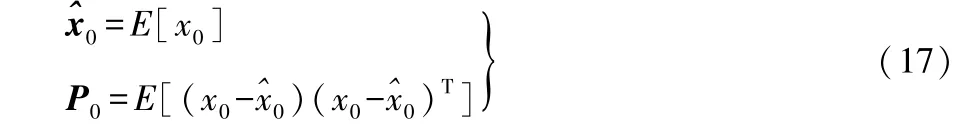
式(17)中:E为期望值;下标0 为初始状态。

②经UT 变换,获取2n+1 个σ采样点

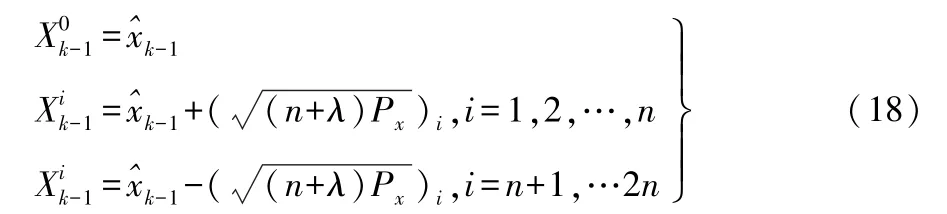
式(18)中:Xk-1为构造的点集;λ为尺度调节因子。

③计算状态变量的状态协方差矩阵

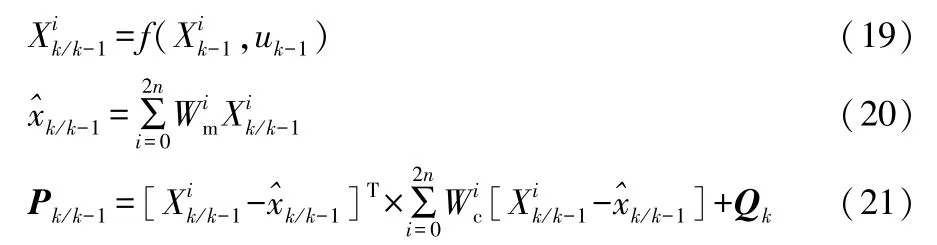
式(20)-(21)中:Wm为均值权重;Wc为对应的协方差权重;Qk为过程噪声协方差矩阵。

④计算系统观测的均值

⑤计算系统观测的互协方差矩阵和协方差矩阵

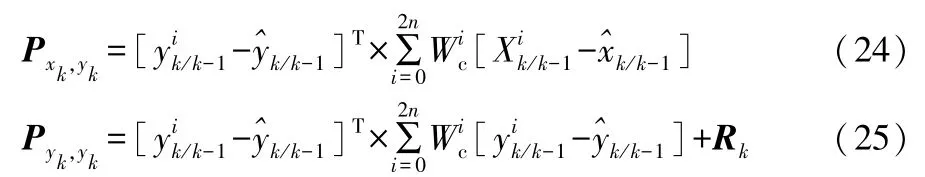
式(25)中:Rk为观测噪声协方差矩阵。

⑥计算卡尔曼增益K

⑦更新系统的状态矩阵和误差协方差矩阵

与EKF 法相比,UKF 法无需对非线性函数进行线性化处理,可直接代入非线性形式的电池模型,进行SOC 估算,减小系统估计误差,提高算法的精度。

3 仿真与结果分析

有关EKF 法的研究较深入,为突出UKF 法的优越性,在MATLAB/Simulink 环境下,分别搭建基于EKF 法和UKF 法的锂离子电池SOC 估计仿真模型,并对比两种算法模型的精度。 仿真验证采用脉冲放电和恒流放电等两种工况。

3.1 脉冲放电工况下的SOC 估计

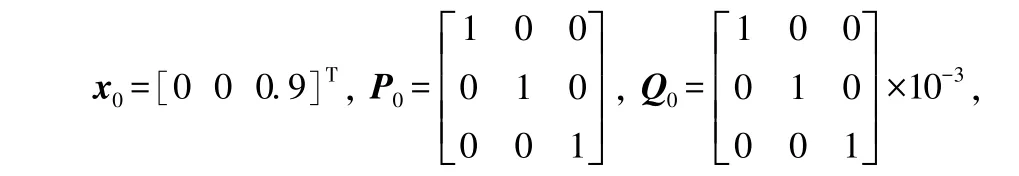
仿真结果如图6 所示。

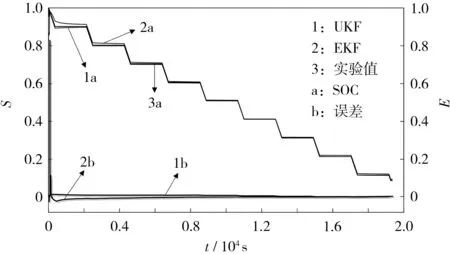
图6 脉冲放电工况下SOC 估计曲线Fig.6 SOC estimation curves at pulse discharge condition

从图6 可知,在仿真初始阶段,由于电池内部电化学反应还未达到稳定状态,估计结果波动都比较大,但随着放电的进行,仿真误差逐渐减小并趋近于0。 EKF 法估计的整体误差稳定在0.04 以内,而UKF 法估计的整体误差稳定在0.01 以内,原因是UKF 法无需对非线性函数进行局部线性化处理,可以直接代入非线性形式的电池模型中进行SOC 估算,提高了算法的精度。 实验结果表明,UKF 法的精确性较好,对误差有良好的矫正性。

3.2 恒流放电工况下的SOC 估计

在常温下,利用电池测试实验平台对满充的锂离子电池进行恒流放电实验,放电电流为0.50C,当电池放电到截止电压时,停止放电。 采集放电过程的端电压、放电电流与放电容量,与仿真结果对比,如图7 所示。

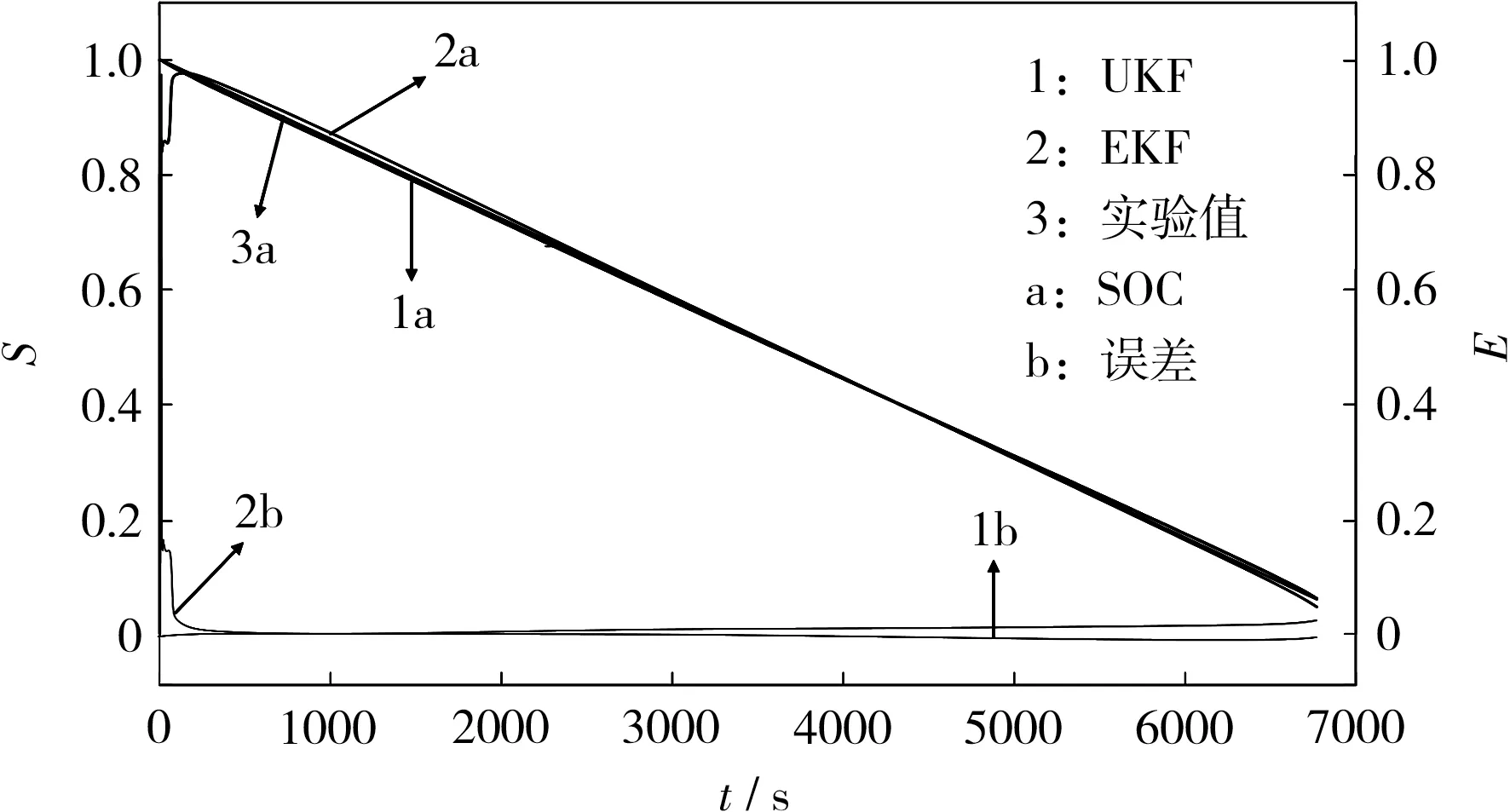
图7 恒流放电工况下SOC 估计曲线Fig.7 SOC estimation curves at galvanostatic discharge condition

从图7 可知,仿真开始时,恒流放电工况仿真结果与脉冲放电工况一样,波动都比较大,但随着放电的进行,仿真误差逐渐减小并趋近0。 EKF 法估计的整体误差稳定在0.012以内,UKF 法估计的整体误差稳定在0.007 以内,再次证明利用UKF 法对电池SOC 进行估计,精确度较高。

4 结论

本文作者首先建立电池二阶RC 等效电路模型,并通过脉冲放电工况实验获得放电端电压曲线,再对端电压曲线进行二阶指数拟合,经计算获取模型离线辨识参数,验证搭建仿真模型验证离线辨识的可行性及准确性。 分别研究EKF法和UKF 法的基本原理,并进行详细介绍;再利用MATLAB仿真软件,在Simulink 环境下,搭建基于EKF 法和UKF 法的电池SOC 估计仿真模型,并分别采用脉冲放电和恒流放电等两种放电工况,验证模型的准确性及算法精度。

从仿真结果可知,对于脉冲放电实验,EKF 法估计整体误差稳定在0.04 以内,而UKF 法估计整体误差稳定在0.01以内。 对于恒流放电实验,EKF 法估计整体误差稳定在0.012 以内,UKF 法估计整体误差稳定在0.007 以内。 相比于EKF 法,UKF 法估计精度更高,收敛性更好,因此UKF 法可以更好地满足电池估计的要求。