“摆球推方块”模型中二者分离位置的数理分析

李 力 高 远 张邦忠

(1. 重庆市清华中学，重庆 400054； 2. 重庆市实验中学，重庆 401320)

在中学物理教学中，常见如下“摆球推方块”模型：[1]如图1所示，长为L的轻杆上端固定一质量为m的小球A(可视为质点)，杆的下端用铰链固接于水平面上的O点，置于同一水平面上质量为M的立方块B恰与A接触。今有微小扰动使杆向右倾倒，从而摆球推着方块向右运动.若不计各处摩擦，试问摆球与方块在何处分离？

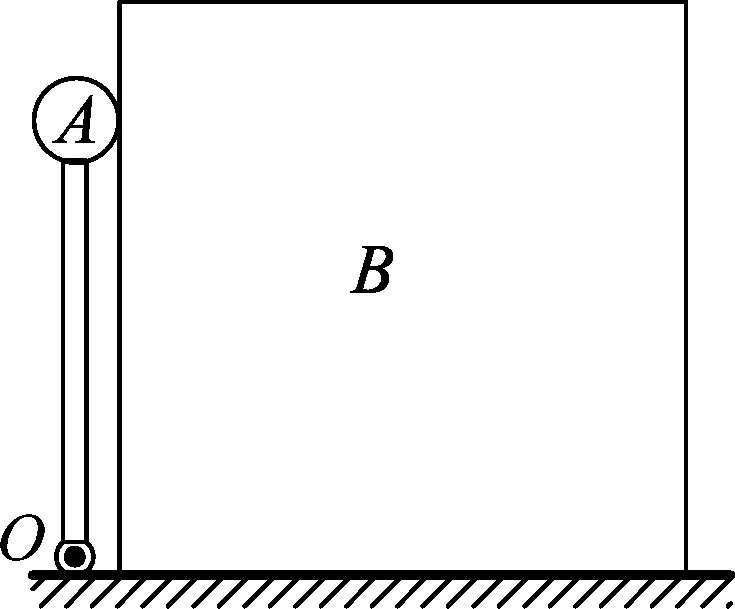
图1

通常凭直觉会判断出，二者分离瞬间轻杆转过的角度θ应该与方块、小球质量比k=M/m有关，而且质量比越大时，即越轻的小球推越重的方块，推动会越困难，所以分离位置应该越滞后.本文将通过数理分析得到它们之间的定量关系，最后探讨与之紧密相关的3个结论及其物理意义.

假设经一段时间，二者位形如图2所示.由速度关联和机械能守恒定律分别得

vAcosθ=vB.

(1)

(2)

令k=M/m，则解得

(3)

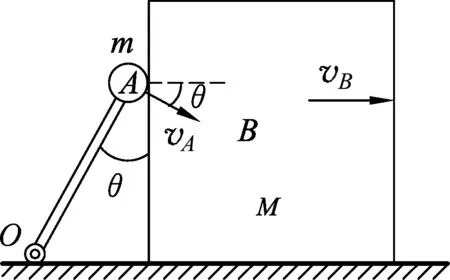
图2

二者分离时方块速度vB最大，从而vB2达到最大.为简便计，可等价考虑以下函数f(θ)的最值：

(4)

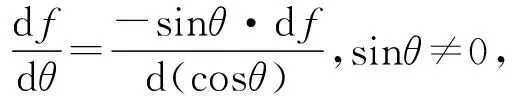
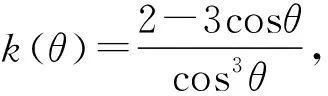
kcos3θ+3cosθ-2=0.

(5)

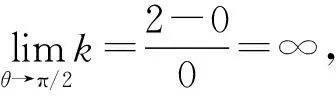
图3

现在研究分离时轻杆对小球的作用力F.首先，通常轻杆对小球的作用力未必沿杆，但本问题中此力必然沿杆方向，原因是：对轻杆考虑对转轴的转动定律，0转动惯量(值为0)乘以有限的角加速度(可以为0)等于为0的外力矩，从而球对杆的作用力必然通过转轴沿杆方向，再由牛顿第三定律知杆对小球的作用力沿杆.换言之，如果小球对杆的作用力不沿杆方向，则外力矩不为0，在不计转动惯量的轻杆上会产生与实际不符的无穷大角加速度.

其次，由于分离瞬间方块加速度为0，从而小球的水平加速度也为0.另一方面，小球所受重力竖直向下，如果沿杆方向轻杆对小球作用力不为0，则水平方向必有其分力，故水平加速度不可能为0，这个矛盾说明分离瞬间必有F=0.由以上分析不难判断出“在分离之前轻杆向外顶小球，之后向内拉小球”.这样可得结论3：“无论质量比k与分离角度θ如何，分离时杆对小球的作用力F均为0”.

分离位置以后，方块以分离瞬间速度水平向右匀速前进，小球继续沿圆弧下摆，其水平速度一直减小直至竖直落地时水平速度为0，可见分离位置之后二者完全分开没有接触.

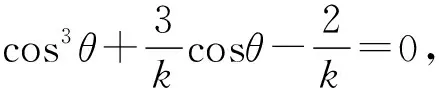
(6)

从(6)式也可看出k→∞时有θ→π/2.(5)式和(6)式其实是分离角度θ与质量比k之间函数关系的两种显式表达和一种隐式表达，它们彼此是等价的.