基于混沌初始化和高斯变异的飞蛾火焰优化算法

刘 倩， 冯艳红,2， 陈嶷瑛

(1.河北地质大学 信息工程学院，河北 石家庄 050031； 2.河北地质大学 河北省智能传感物联网技术工程研究中心，河北 石家庄 050031 )

0 引言

飞蛾火焰优化算法(moth-flame optimization algorithm，MFO)[1]是一种新颖的群体智能算法。该算法由飞蛾和火焰2部分构成，通过横向定位导航机制来解决探索和利用之间的平衡问题。MFO具有参数简单、容易实现且鲁棒性好等优点，因此，自提出以来，便受到国内外学者的广泛关注，使其在诸多领域得到应用[2-5]。当前，国内外学者对其改进研究主要分为对飞蛾飞行方式的优化和对进化机制的优化。

尽管已有文献对MFO算法的改进在一定程度上提高了算法的性能，但是这些改进措施在解决高维多峰复杂问题时效果不尽如人意。

基于此，本文提出一种基于混沌初始化和高斯变异的飞蛾火焰优化算法(moth-flame optimization algorithm based on chaotic initialization and Gaussian mutation, CGMFO)。CGMFO采用立方混沌映射初始化种群以增强飞蛾勘探未知空间的能力，从而提高求解精度；采用高斯变异对部分较差个体进行局部扰动以提高算法的收敛速度；采用阿基米德曲线飞行机制以增强种群的多样性，并抑制算法的早熟收敛，进而实现全局最优化。CGMFO对CEC14经典测试函数[6]和21个可扩展Benchmark函数[7]进行求解，实验结果验证了该算法具有良好的收敛能力和竞争实力。

1 飞蛾火焰优化算法的基本原理

在MFO算法中，用式(1)表示飞蛾种群规模为n，维数为d的飞蛾所处空间位置，且用式(2)矩阵存储飞蛾个体的适应度值。火焰是算法的另一个核心，其在空间的位置矩阵与飞蛾的空间矩阵类似，用式(3)表示，使用式(4)矩阵存储相应火焰的适应度值。

(1)

OM=[om1,om2,…,omn]T；

(2)

(3)

(4)

火焰减少过程如下式所示：

(5)

式中：t和T分别为当前迭代次数和最大迭代次数；N为最大火焰数量。

Di=|Fj-Mi|。

(6)

式中：Di为飞蛾Mi到火焰Fj的距离。

假设飞蛾Mi会朝着距离自己最近的火焰Fj移动，移动的路径选取了对数螺线曲线,并将该曲线作为飞蛾的主要更新机制，算法的对数螺旋曲线定义如下：

S(Mi,Fj)=Di·ebt·cos 2πt+Fj。

(7)

式中：S(Mi,Fj)为更新后的飞蛾位置；Di表示第i个飞蛾与第j个火焰的距离；b为与螺旋形状相关的常量；t为随机数，取值区间为[-1,1]；ebt·cos 2πt为对数螺旋曲线表达式。

总结前文所述，飞蛾火焰优化算法的一般步骤如下：

步骤1初始化算法参数：飞蛾数量n、维数d、最大迭代次数T等，随机初始化种群；

步骤2计算种群中飞蛾的适应度值，并按适应度值升序排序；

步骤3利用式(5)更新火焰数量；

步骤4利用式(6)计算飞蛾到火焰的距离；

步骤5利用式(7)更新飞蛾位置；

步骤6若满足给定的迭代次数，算法结束，获得最优解；否则，返回步骤2。

2 CGMFO原理

2.1 混沌初始化

在原始MFO中，飞蛾的位置通过随机初始化的方式产生，会造成飞蛾的位置分布不均匀，进而降低求解精度。而基于混沌理论的混沌序列具有伪随机性和边界性等特点，故许多学者提出了嵌入混沌序列的多种算法[8-9]。在诸多混沌映射中，立方映射的性能较优[10]，因此，本文采用立方混沌映射对MFO进行初始化：

(8)

利用立方混沌映射初始化飞蛾种群的3个步骤如下：

步骤1按照式(8)随机产生d维空间中的n只飞蛾，即Y=(y1,y2,y3,…,yd)，yi∈[-1,1],i=1,2,…,d；

步骤2将每只飞蛾的每一维迭代n次，从而产生n只飞蛾；

步骤3在所有的飞蛾迭代完成后，按照式(9)映射到解空间中。

(9)

式中：Ud、Ld为搜索空间的上、下界；yid是利用式(8)产生的第i只飞蛾的第d维坐标；xid是第i只飞蛾在搜索空间第d维的坐标。

本文将基于立方混沌映射初始化的飞蛾火焰优化算法记为CMFO。

2.2 高斯变异机制

观察MFO算法中解的更新公式(式(5)和式(7))，可以发现每只飞蛾空间矢量位置的更新与离其最近的火焰空间位置有直接的关系。而此火焰空间位置仅靠适应度值来确定，这就导致对当前全局最优飞蛾的有效利用能力不强。

因此，在对飞蛾按适应度值进行排序后，选取适应度值最差的n×ω个个体，并对其应用高斯变异Gaussian(μ,σ2)，其中，n是飞蛾种群规模；ω是变异的比例；μ表示均值；σ2表示方差。根据经验，本文ω取值为1/6，便于控制和缩小更新范围，并适度地提高算法的种群多样性。改进后的飞蛾产生公式描述如下：

(10)

本文将基于CMFO，对种群每一代中少数较差个体用高斯变异进行微小扰动的飞蛾火焰优化算法记为GCMFO。

2.3 基于阿基米德曲线的飞行机制

由于MFO中飞蛾的飞行机制会影响算法的性能，与对数螺旋曲线相比，阿基米德螺旋曲线使飞蛾扩大了搜索范围，且阿基米德螺旋曲线在诸多优化领域得以应用[11-12]。为了增强MFO算法的种群多样性，加快算法的收敛速度，本文将原MFO算法中的对数螺旋曲线替换为阿基米德螺旋曲线。其平面笛卡尔坐标方程式为

(11)

其中，当θ=0时，α为起点到极坐标原点的距离，β为螺旋线每增加单位角度随之对应增加的数值。当θ>0时，α相当于旋转螺线，而β则控制相邻两条曲线之间的距离。

则飞蛾位置的移动如下式所示：

S(Mi,Fj)=Di·ebt·(α×γ)·sin 2πβ(γ-α)+Fj。

(12)

其中，b=1，β=10，α、γ定义如下：

(13)

γ=(α-1)×rand+1。

(14)

式中：rand为随机数，取值区间为[-1, 1]。

本文将基于GCMFO，应用阿基米德螺旋曲线的飞行方式的飞蛾火焰优化算法记为CGMFO。

2.4 CGMFO算法流程

根据2.1～2.3节描述的算法改进思想，提出的CGMFO算法步骤如下：

步骤1按式(8)和式(9)初始化种群；

步骤2计算种群中飞蛾的适应度值，按适应度值升序排序；

步骤3选择排序后适应度较差的1/6飞蛾，按式(10)进行高斯变异，然后求解飞蛾和火焰的适应度值，选择其中最好飞蛾个体的位置并将其保存为火焰适应度值矩阵；

步骤4利用式(5)更新火焰数量；

步骤5利用式(6)计算飞蛾到火焰的距离；

步骤6利用式(13)和式(14)初始化螺旋曲线的相关参数，按式(12)更新飞蛾位置；

步骤7若满足给定的迭代次数，算法结束，获得最优解；否则，返回步骤2。

3 数值实验及分析

3.1 环境与参数

为了比较不同改进策略对MFO的影响程度，本文进行了2组实验。第1组实验对CGMFO、GCMFO、CMFO与MFO这4种算法，选用CEC14测试集[6]中f1～f6进行仿真实验比较。第2组实验对CGMFO、MFO、GA[13]、ABC[14]、PSO[15]、DE[16]、FPA[17]和BOA[18]这8种算法，利用21个可扩展Benchmark函数[7]进行仿真实验比较。

仿真硬件环境为LENOVO Intel i7-8750H CPU 2.21 GHz，8.00 GB RAM，操作系统为Windows 10，利用MATLAB R2018b编程实现。

所有算法均采用相同的种群规模n=30，最大迭代次数T=1 000，第1组实验中，维数d=100，第2组实验中，d=10，重复实验次数RepeatCount=30。各算法的其余参数设置如表1所示。

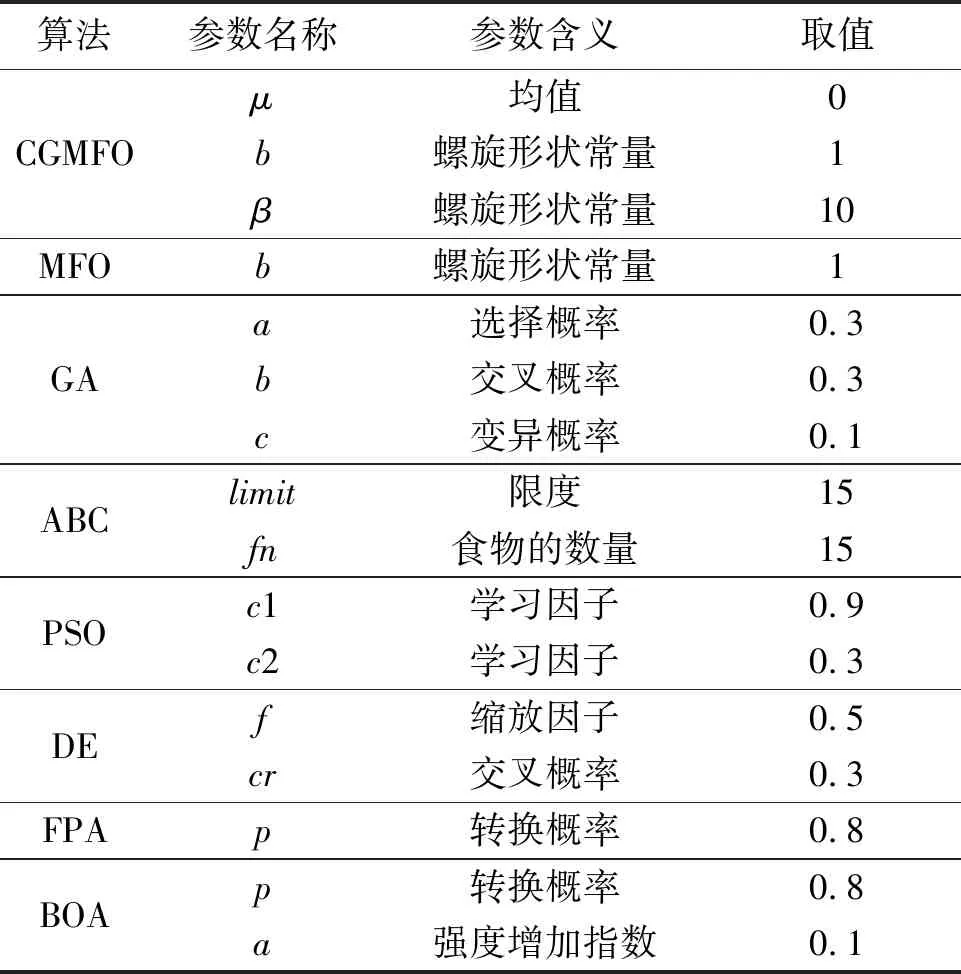
表1 8种算法的参数设置Table 1 Parameter settings for 8 algorithms

3.2 算法性能评价指标

本文的2组实验都采用优化均值误差(Average)和标准方差(Std.Dev)评价算法的优化能力，其中

优化均值误差计算如下：

Average=f(x)-f(x*)。

(15)

式中：x表示算法得到的解；x*表示每个测试函数的理论最优解。Average越小，则解的质量越好。

第2组实验中增加了Best最优解和Worst最差解的比较，这2个值越小，说明解的精度越高。

同时，为了比较算法在统计意义上的差异性，利用Wilcoxon秩和检验(显著水平α=0.05)分别对21个函数的实验结果进行统计分析。

3.3 实验结果分析

3.3.1 第1组实验结果分析

由于篇幅有限，表2给出了4种算法对CEC14中每个函数进行30次独立实验的部分计算结果， 由表2的计算结果可以得出如下结论：

表2 4种算法对于CEC14测试函数的实验结果比较Table 2 Comparison of the experimental results of the 4 algorithms for the CEC14 test function

(1)3种改进算法对于CEC14中的测试集函数f1～f6，无论是优化均值误差还是标准方差均优于原始的MFO。

(2)CMFO只使用立方混沌映射产生混沌序列，保证了飞蛾个体初始化位置在整个搜索空间的均匀分布，优化均值误差和标准方差在绝大多数测试函数上均有提高。

(3)GCMFO的改进效果优于CMFO，这是由于GCMFO不仅采用了立方混沌映射初始化，而且通过高斯变异对每代中少数较差的个体进行扰动，帮助算法跳出局部极值区域，提高了算法收敛速度。

(4)CGMFO的改进效果明显优于其他2种改进算法，多个函数的误差均值和标准方差都接近理论最优。

3.3.2 第2组实验结果分析

表3为8种算法对21个可扩展Benchmark函数进行30次独立实验的计算结果，其中Best为最优解，Worst为最差解，Average和Std.Dev定义与第1组实验相同。表3中的符号†、≈、■分别表示CGMFO算法的实验结果优于、相当于和劣于对比算法，其中结果加粗表示最优。为了进一步比较CGMFO与其他7种算法的收敛趋势，图1给出了8种算法求解Benchmark函数f1～f3、f9～f11各30次的平均进化曲线。经多次实验发现，当>设定每种算法的迭代次数均为T=160时，进化曲线的效果明显，故这里将T设置为160。

由以上实验结果可知：

(1)由表3可以看出，对于21个Benchmark函数，针对4种评价指标，CGMFO在求解几乎全部问题上均优于其他7种比较算法。其中14个函数求解结果达到了理论最优(f1～f8、f11～f13、 f18、 f20、f21)。其余未达到理论最优值的7个函数，与其他算法相比，CGMFO也最接近理论最优。

表3 8种算法对于测试函数f1～f21的部分实验结果比较Table 3 Comparisons of some experimental results of 8 algorithms for test functions f1 to f21

(2)由图1的平均迭代进化曲线可以看出，在21个可扩展Benchmark函数中,CGMFO对应的目标函数下降曲线比其他7种算法的下降曲线具有更快的下降速度，并很快达到了最优值。这再次表明，CGMFO在函数全局优化方面具有更好的有效性，收敛速度更快。

图1 部分平均迭代进化曲线Figure 1 Some average iterative evolution curves

4 结论

针对MFO求解精度不高及易陷入局部最优等缺陷，本文从3个方面对算法进行改进：立方混沌映射初始化，有效地防止飞蛾的位置分布不均匀；高斯变异对较差个体的扰动，减少了算法陷入局部最优的可能；阿基米德曲线飞行机制的应用使种群的多样性有所增加。从实验结果看出，CGMFO在搜索性能上均优于CMFO和GCMFO，且CGMFO在求解精度和收敛速度上与文中的其他进化算法相比，均表现优秀。由于MFO提出时间不长，故算法的参数分析和在工程问题中的应用将是下一步的研究课题。