基于时延和负载均衡的多控制器部署策略
刘振鹏, 王鑫鹏, 李 明, 任少松, 李小菲
(1.河北大学 电子信息工程学院,河北 保定 071002;2.河北大学 信息技术中心,河北 保定 071002)
0 引言
随着网络规模的增大,如何优化网络性能成为至关重要的问题。软件定义网络(software define network,SDN)是近年来新兴的一种网络结构,它将网络的控制层和数据层解耦,利用集中式的控制器对底层设备进行可编程化管理,进而实现对网络资源的灵活调配[1]。然而,随着大数据时代的到来,在大范围的SDN网络中部署健壮的控制平面仍然是一个主要的挑战。为了解决这些问题,引入了一个逻辑上集中、物理上分布的控制平面[2]。这种类型的控制体系结构通常由多个控制器组成,这些控制器之间彼此相互通信,Kandoo[3]就是这种类型的一个例子。但在引入这一体系的同时,也出现了多个控制器如何部署的问题。
目前,已经有很多对SDN控制器部署研究的文献。文献[4]首次提出控制器部署问题是一个NP问题,以平均时延和最大时延为指标,选择控制器位置。文献[5-8]提出了几种基于群体的智能优化算法,通过考虑时延作为单一目标参数来求解控制器最优部署位置。以上文献在研究控制器时延问题上均取得不错的效果,但在实际SDN环境下,控制器的负载能力也是一个不可忽略的因素。文献[9]提出了基于控制器的负载平衡因子,在已知控制器数量的情况下,通过最小化负载平衡因子和总流请求代价来获得特定控制器的位置。文献[10]为了保证控制器负载均衡和相对较低的时延,提出了一种基于层次K-means算法的多控制器部署方案,但该方案只考虑控制器子域如何分配交换机数量,在单个控制器的负载能力上未作考虑。文献[11]提出一个控制器位置-分配模型,引入公平负载分配函数来平衡控制器负载,并减少控制器之间的时延,但该方案未对整个网络总体性能进行分析。
为此,本文综合考虑SDN环境下控制器的时延和负载问题,提出控制器部署算法(MCP),并用改进的粒子群算法(APSO)和MCP算法结合的APSO_MCP算法解决多控制器部署问题。
1 控制器部署模型
1.1 问题描述
在SDN架构中,控制平面的控制器作为决策和信息收集的角色管理着数据平面的交换机,交换机与控制器之间的请求时延和处理时间影响了SDN网络的整体性能。数据包到达控制器和完成处理返回的时间由2个因素共同决定,分别是交换机与控制器之间的距离和控制器管理的交换机数量。交换机与控制器之间的距离决定了传播时延;而控制器管理的交换机数量决定了控制器的负载容量,即决定了流量转发请求处理的时间。
时间延迟是影响网络性能的一个重要因素。在SDN网络中,时间延迟包括4个方面:传输、传播、排队和处理时延。对广域网而言,在控制器不过载的前提下,传播时延远超过其他时延,其他3种时延影响很小,可以忽略[12]。因此,在考虑时间延迟因素时选择控制器和交换机之间的传播时延。
负载是控制器的重要指标。如果控制器负载过重就会导致其无法掌握实时的网络状态,造成网络性能瓶颈。因此,将SDN的广域网划分为多个子域的网络,合理分配各个子域内的交换机数量,可以提高控制器的服务质量,并且还可以限制广播风暴。
因此,本文考虑在平衡控制器负载能力的同时,最小化交换机和控制器之间的传播时延。
1.2 系统模型
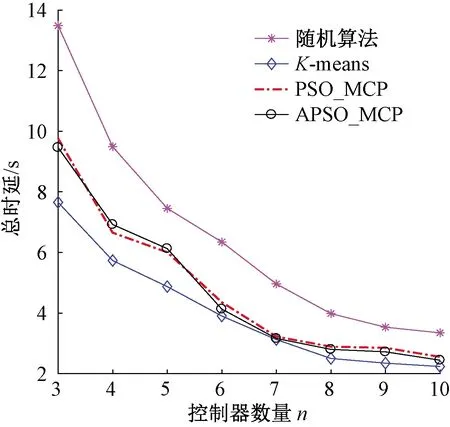
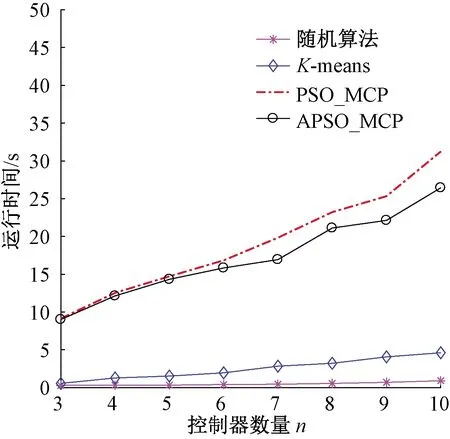
用无向图G(V,E)来表示物理网络拓扑,V和E分别表示节点集合和边的集合。n=|V|表示节点的个数。节点集合的每个节点都是交换机的位置,则有交换机集合S={s1,s2,…,sn}。假设节点集合中的每个节点都可能是控制器部署的位置,需要在网络中部署k(k Dp∩Dq=∅,∀p,q∈[1,k],p≠q。 (1) 每个交换机只能由一个控制器控制,即 (2) 其中,当交换机Si由控制器Cj控制时,δSiCj=1,否则δSiCj=0。 每个控制器可以同时管理多个交换机,每个交换机只在一个控制器子域内,则有: (3) (4) 式中:m为单个控制器管理的交换机个数;n为k个控制器管理的交换机个数之和。 1.2.1 时间延迟 交换机和控制器之间的时延在控制器部署问题中是一种常用的度量方式,单个交换机和控制器之间的传播时延可用式(5)表示: (5) 式中:dSiCj为交换机Si和控制器Cj之间的传输距离;vc为数据在链路中的传输速度。 各个控制器子域的传播时延和整个网络的总时延可由式(6)和式(7)分别表示: ; (6) (7) 为了衡量整个网络的控制器部署在时延方面的合理性,引入传播时延标准差ξT来评判各个控制器子域的传播时延与整个网络的总传播时延之间的差异,由式(8)表示: (8) (9) 式中:ξTmax为最差传播时延标准差;ξTmin为最优传播时延标准差。 1.2.2 负载均衡 在网络G(V,E)中,存在n个交换机,每个交换机的负载请求表示为λSiCj,则每个控制器子域的负载请求λCj为: (10) 其中,每个控制器子域内的负载λCj不能大于控制器Cj自身的最大负载能力λCj max,即满足: λCj≤λCjmax。 (11) 整个网络的总负载和平均负载可由式(12)和式(13)表示: (12) (13) 为了衡量整个网络在负载方面的合理性,引入了负载均衡标准差ξL来评判各个控制器子域的负载与整个网络的平均负载的差异,如下所示: (14) (15) 1.2.3 控制器部署模型 针对以上以传播时延差异性和负载差异性为指标的多控制器部署问题,可以找到一个合适的部署方案,即使以上指标最小化,为此提出控制器部署模型为 (16) 其中, α+β=1,0≤α,β≤1。 (17) 式中:F为优化目标,是整个网络的性能;参数α、β为调节目标函数的影响权重,参数α越大,越注重网络整体的传播时延差异性,参数β越大,越注重网络整体的负载差异性。 为解决上述问题,根据建立的模型提出多控制器部署算法(multi-controller placement,MCP)。MCP算法的目的是在保证整个网络较高的负载均衡性能的基础上降低各个控制器子域的传播时延,从而保证整个网络的总时延相对较低。 控制器部署算法分为3个阶段:①网络拓扑数据预处理(Step 1~3);②选取控制器部署位置(Step 4);③控制器子域部署交换机(Step 5~18)。在网络拓扑数据预处理阶段,将无向图G(V,E)中节点和边的数据矩阵转换成距离矩阵,并通过Johnson全源最短路径算法可以计算出每个节点到其他所有节点的最短距离。在选取控制器部署位置阶段,采用粒子群算法初始化控制器部署位置。在控制器子域部署交换机阶段,以距离最近原则开始构建子网(Step 5~10),当各个控制器子域管理的交换机个数相同且均等于⎣n/k」时,如果网络中还有未被分配的交换机节点,对剩下的交换机节点继续按照距离最近原则进行分配,直到所有控制器节点都被分配(Step 11~18)。至此,k个负载均衡的控制器子域分配结束。 通过改进的粒子群算法初始化控制器部署位置,确定控制器管理的交换机数量⎣n/k」,这样可以保证整个网络的负载均衡,接着选择与各个控制器距离最近的交换机进入各控制器子域,这样可以保证每个控制器子域的传播时延尽可能小。当各个控制器子域管理的交换机个数相同且均等于⎣n/k」时,优先按照距离最近原则分配交换机。这样可以保证剩余的交换机和控制器间的传播时延,牺牲了部分负载均衡性能。整个过程2种目标互相折中,从而使得整个网络的性能达到最优。 由于整个网络系统的负载不均衡主要集中在初始分配时期,使用MCP算法可以更好地确定控制器的位置和各控制器子域管理的交换机,使得整个网络的初始分配时期获得一个更良好的布局,可以有效降低动态网络中多控制器部署中出现的阈值过载现象。MCP算法的描述如下。 算法1控制器部署(MCP)。 输入:网络拓扑G(V,E),控制器个数k; 输出:控制器部署矩阵place_value。 Step1使用Haversine公式[13]计算出拓扑上节点间距离; Step2使用Johnson全源最短路径算法计算出单个节点到所有节点的最短距离; Step3使用式(5)计算出单个节点到所有节点的最小时延; Step4使用粒子群算法选择k个控制器的初始位置作为被部署的控制器集合C={c1,c2,…,ck}; Step5找到控制器集合C={c1,c2,…,ck}与所有交换机集合S={s1,s2,…,sn}之间的最小时延; Step6将最小时延放到控制器部署矩阵place_value(n,k)对应位置; Step7将最小时延对应的交换机节点si放到被挑选的交换机集合select_switch{si}; Step8将最小时延对应的控制器节点cj放到被挑选的交换机集合select_controller{cj}; Step9统计select_controller集合中c1,c2,…,ck的个数; Step10重复Step 5~9直到select_controller集合中c1,c2,…,ck的个数都等于⎣n/k」; Step11从交换机集合S中选择select_switch集合中没有出现的元素si,形成集合S′={si}; Step12找到交换机S′={si}集合与控制器集合C={c1,c2,…,ck}之间的最小时延; Step13将最小时延放到控制器部署矩阵place_value(n,k)对应位置; Step14将最小时延对应的交换机节点放到被挑选的交换机集合select_switch{si}; Step15将最小时延对应的交换机节点si从S′集合中移除; Step16将最小时延对应的控制器节点cj从C={c1,c2,…,ck}集合中移除; Step17统计select_switch集合中所有元素的个数; Step18重复Step 12~17,直到select_switch集合中所有元素的个数等于n; Step19返回控制器部署矩阵place_value。 2.2.1 粒子群算法(PSO) 粒子群算法(particle swarm optimization,PSO)是一种源于自然的基于种群的随机优化算法[14]。粒子群算法在群体中寻找最优解,并从两种学习方式中获益:基于个体历史的认知学习和基于群体历史的社会学习[15]。初始阶段,认知学习需要确定最优位置,在获取局部最优后,社会学习来决定全局最优位置。 假设有n个群体表示潜在的解决方案,每个群体都可以用d维向量表示。在粒子群算法中, 每个粒子包含2个分量:速度和位置[16]。当前的粒子群位置向量用Xi=[xi1,xi2,…,xid](i=1,2,…,n)表示。当前的速度向量用Vi=[vi1,vi2,…,vid]表示。粒子群的局部最优位置为Pi=[pi1,pi2,…,pid],Pgb为全局最优位置向量。 在t+1时刻,更新粒子群的位置Xid和速度Vid分别表示为: (18) (19) 式中:ω为惯性权重;r1和r2为[0,1]的随机数;c1和c2分别为调整个体部分的局部学习因子和调整社会部分的全局学习因子。 一个大的惯性权重ω有利于展开全局寻优,而一个小的惯性权重值有利于局部寻优。因此,采用时变权重,在迭代过程中采用线性递减惯性权值,则粒子群算法在开始时具有良好的全局搜索性能,能够迅速定位到接近全局最优点的区域,而在后期具有良好的局部搜索性能,能够精确地得到全局最优解。时变权重的表达式如下: ω=ωmax-((ωmax-ωmin)/Imax)×I。 (20) 式中:Imax为最大迭代;I为当前迭代;通常ωmax和ωmin分别取0.9和0.1。 每个粒子的最优位置向量为 (21) 2.2.2 改进的粒子群算法 针对PSO算法出现的收敛速度慢的缺点,采用改进的粒子群优化算法(advanced particle swarm optimization,APSO)以改善种群的收敛速度。 由于PSO算法的搜索过程是一个非线性的复杂过程,采用惯性权重线性过渡的方法并不能正确地反映真实的搜索过程。因此引入文献[17]中收敛因子概念,从提高种群的收敛速度方面对粒子群算法进行改进。其中收敛因子表达式为 (22) 对粒子群算法的速度方程稍加改进,可得到: (23) 根据式(23)可以更新粒子的飞行速度。文献[18]证明了采用收敛因子的优化算法相比于采用惯性权重的优化算法有更好的收敛速度。 2.2.3 改进的粒子群算法实现控制器部署(APSO_MCP) 在改进的粒子群算法中,通过迭代,使多个粒子并行搜索最优解,并确定最小合适度时控制器的位置。控制器位置向量是上述目标函数的次优解,每个个体都表示控制器部署的一种方式。在给定控制器数量为k个的情况下,单个粒子的位置向量为Pi=[pi1,pi2,…,pik]。APSO_MCP算法将所有节点的经纬度latlon、需要被部署的控制器数量k、最大迭代maxIt作为输入,最后得到控制器的最终部署位置Pgbest,整个网络的最优合适度F(Pgbest)。APSO_MCP算法的描述如下。 算法2APSO_MCP算法。 输入:所有节点的经纬度latlon,被部署的控制器数量k,最大迭代次数maxIt; 输出:最终的控制器部署位置Pgbest,全局最优合适度值F(Pgbest)。 (1)初始化阶段: ①初始化学习因子c1,c2,收敛因子χ,粒子群nPop,将粒子群全局最优合适度F(Pgbest)设置为∞ ; ②fori=1 tonPop ③ 随机部署k个控制器部署位置Pposition,并将当前位置设为当前最优位置Ppbest; ④ 初始化粒子的速度Pvelocity为0; ⑤ 调用控制器部署算法(MCP),调用合适度函数F; ⑥ if(F(Ppbest) ⑦ 将局部最优位置Ppbest设为全局最优位置Pgbest; ⑧ 将局部最优合适度F(Ppbest)设为全局最优合适度F(Pgbest); ⑨endif ⑩endfor (2)优化阶段: 粒子合适度函数F通过式(5)~(17)来计算。 相关算法均在MATLAB中运行,选择的仿真环境是MATLAB 2018a,系统配置是Windows 10 64位系统,i5处理器,8 GB内存。实验采用的网络拓扑选自于网络拓扑动物园的Xspedius网络。Xspedius网络有34个节点和49条边。设置控制器的最大负载为1 600 flows/s,各个交换机的流请求相互独立且为100 flows/s[19]。设置vc为3×108/s,设置粒子群种群数量为50,迭代次数为300。设置控制器部署模型权重因子α为0.5,β为0.5。 为了使实验仿真更具有说服力,选用随机算法和K-means算法做对比。随机算法是面对大量的数据,从其中随机选取一些数据来进行分析。K-means算法是输入聚类个数k,以及包含n个数据对象的数据库,输出满足标准方差最小的k个聚类的一种算法。将APSO_MCP算法、随机算法[7]、K-means算法[20]和PSO_MCP算法[7]在网络总时延、负载均衡比、总体性能以及运行时间方面进行比较。 实验1验证随机算法、K-means算法、PSO_MCP算法和APSO_MCP算法在控制器传播时延上的差异。如图1所示,由于改进的粒子群算法是在收敛速度的基础上进行改进,故APSO_MCP算法和PSO_MCP算法在控制器传播时延上的差异不大;在控制器数量为3、4、5时,APSO_MCP算法和K-means在总时延的差别较大;随着控制器数量的增加,APSO_MCP算法在总传播时延方面接近于K-means算法。出现这种情况的原因是K-means算法在部署控制器时根据最小距离原则选择和更新控制器位置,而本文算法选择增加部分传播时延来平衡负载均衡指标。 图1 网络总时延比较Figure 1 The comparison about the total latency of the network 实验2验证随机算法、K-means算法、PSO_MCP算法和APSO_MCP算法在整个网络最大负载控制器子域和最小负载控制器子域之间的差异。实验结果如图2所示,APSO_MCP算法和PSO_MCP算法的实验结果相近,始终接近于理想参数1,优于K-means算法和随机算法。分析其原因是:网络拓扑中节点分布不均匀,小部分分散,大部分相对集中,而K-means是以减少传播时延为目标,在划分控制器子域时未考虑控制器子域的负载,从而导致部分控制器子域内的负载大幅增大。 图2 网络负载均衡比比较Figure 2 The comparison about the load balance ratio of the network 实验3验证随机算法、K-means算法、PSO_MCP算法和APSO_MCP算法在整个网络的性能上的差异。实验结果如图3所示,APSO_MCP算法和PSO_MCP算法在整个网络的总体性能上相近。在控制器数量为3、4、5时,随机算法、K-means和APSO_MCP在整个网络的性能的差别较大。出现这种现象的原因是网络拓扑结构中节点分布不均匀,使用K-means算法划分子域后,各个控制器子域的传播时延和整个网络的总时延、各个控制器子域之间的负载和整个网络的平均负载相差较大,从而导致整个网络的性能降低。随着控制器数量的增加,K-means算法和随机算法在整个网络的性能方面接近于APSO_MCP。分析其原因是随着K-means算法划分的控制器子域数量的增多,每个子域管理的交换机数量逐渐减少,整个网络被划分成的控制器子域在传播时延和负载均衡方面越来越合理,整个网络的性能越来越稳定。 图3 网络的总体性能比较Figure 3 The comparison about the overall performance of the network 实验4验证随机算法、K-means算法、PSO_MCP算法和APSO_MCP算法在运行时间上的差异。如图4所示,随机算法的运行时间低于K-means算法、PSO_MCP算法和APSO_MCP算法。随机算法没有迭代过程,故运行时间最短。K-means算法随着控制器数量、迭代次数增加,运行时间逐渐增长。而APSO_MCP算法由于引入收敛因子,种群的收敛速度加快,在运行时间方面优于PSO_MCP算法,种群的收敛速度提升约6.3%,并且随着控制器数量的增加,APSO_MCP算法的收敛速度快的优势越来越明显。 图4 运行时间比较Figure 4 Comparison of the computing time (1)针对软件定义网络中多控制器部署问题,以时间延迟和负载为双重优化目标,建立控制器部署模型,提出MCP算法。结果表明该算法可以保证多控制器子域之间的负载均衡性能,并且有效降低整个网络的时间延迟,从而确保了整个网络的总体性能处于最优的状态。 (2)针对传统粒子群算法收敛速度慢问题,引入收敛因子概念,提出APSO算法。结合APSO算法和MCP算法来部署多控制器位置。结果表明APSO_MCP算法和PSO_MCP算法相比,有效地缩短了算法的运行时间,验证了本文提出的APSO_MCP算法可以有效地提高种群的收敛速度。 (3)合理部署控制器位置的算法可以提升网络性能[21]。然而本文提出的算法还有一些不足,提出的是一种静态的部署算法,在实际网络中,网络状态不断变化,还需要考虑动态网络中的负载情况。
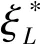
2 控制器部署和改进的粒子群算法
2.1 控制器部署算法(MCP)
2.2 改进的粒子群算法
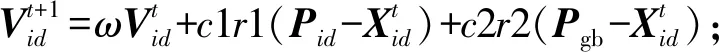
3 仿真实验
3.1 实验设置
3.2 实验结果及分析


4 结论

