基于AHP-BN法的溃坝生命损失风险评价

葛 巍， 焦余铁， 洪辛茜， 段志昌， 李宗坤， 高卫星

(1.郑州大学 水利科学与工程学院，河南 郑州 450001； 2.代尔夫特理工大学 技术、政策和管理学院，荷兰 代尔夫特 2628 BX； 3.云南大学 国际河流与生态安全研究院，云南 昆明 650500； 4.郑州大学 政治与公共管理学院，河南 郑州 450001)

0 引言

作为一种低概率高损失事件，水库大坝一旦溃决，不仅影响水库自身的功能和效益，而且可能会导致巨大的生命损失，给下游居民带来无法消除的精神痛苦和心理恐慌，造成社会难以承受的不良影响。2018年老挝Xe-Pian Xe-Namnoy水电站溃坝，造成35人死亡[1]；2018年新疆射月沟水库溃坝，造成20人死亡[2]。因此，溃坝生命损失风险评价一直为水库大坝风险管理领域所关注。

Brown等[3]应用经验统计的方法对24座大坝溃坝生命损失的历史数据进行分析，建立了一个简单的溃坝生命损失经验估算公式；Dekay等[4]对其改进，得到了一个包含风险人口、警报时间、洪水严重程度与生命损失关系的公式；周克发等[5]根据历史数据，提出更符合中国实际的溃坝生命损失评价模型；Peng等[6]提出了一种基于贝叶斯网络并结合蒙特卡罗算法，考虑了更多影响生命损失的因素与各因素之间内在关系的溃坝生命损失评价模型(HURAM)。此类结合致灾机理分析的经验模型使用简单，但由于中国溃坝历史资料缺乏，在进行资料回归分析时不得不面临小样本的问题，限制了其准确性。

王志军等[7]把地理信息系统(geographic information system，GIS)技术引入到溃坝生命损失评估中；杨胜梅等[8]利用空间信息技术对溃坝洪灾特征参数进行估算，对溃坝生命损失进行评估；石振明等[9]采用地理信息工具快速获取坝址和上下游河道三维地形信息，构建了堰塞湖溃坝快速定量风险评估方法。此类结合计算机模拟和GIS的区域损失叠加分析法计算精度高，但是数据采集工程量巨大且操作过于复杂，实际应用中存在很大难度，不适合对大量大坝进行生命损失风险评价[10]。

层次分析-贝叶斯网络法(analytic hierarchy process-Bayesian network，AHP-BN)将层次分析法(analytic hierarchy process，AHP)和贝叶斯网络(Bayesian network，BN)相结合，不仅能解决评价中的不确定性问题，而且充分考虑要素权重和要素发生概率，减少评价主观性，从而得出客观准确的评价结果[11-12]。

1 溃坝生命损失评价指标体系的构建

溃坝生命损失模型涉及的评价指标繁多且复杂：既有定性指标，又有定量指标，部分指标受到工程因素和人为因素的共同作用，因此科学合理地选择评价指标应遵循以下原则[13]：

(1)科学性。选取的指标应能对溃坝生命损失进行客观准确的描述。

(2)系统性。选取的指标能在各个部分形成一个有机的整体，且具有一定的层次性。

(3)典型性。选取的指标应具有代表性。例如，洪水的危险性与洪水严重性程度、流量、淹没范围与淹没历时等因素有关，目前国内外已有研究成果认为洪水严重性程度更具有代表性[14]，因此指标应选取洪水严重性程度。

(4)可操作性。选取的指标的数据应易于收集且适于分析计算。例如溃坝期间的天气是无法预测的，也很难确定其概率，现有的研究成果也指出该因素的重要性偏低，所以这类指标暂不予考虑。

(5)定量与定性相结合。充分考虑指标是否易于量化，采用定量与定性相结合的原则可以保证评价结果的科学性。

根据以上指标选取原则，选取溃坝洪水严重性程度、风险人口、警报时间、溃坝理解程度、青壮年比例、溃坝发生时间、救援能力、建筑物质量8个指标。溃坝洪水造成生命损失是致灾因子、孕灾环境和承载体的综合体现[15]，因此可从危险性、易损性和防御性3个角度将指标进行分类，从而构建溃坝生命损失评价指标体系，如图1所示。

图1 溃坝生命损失评价指标体系Figure 1 Evaluation index system for life loss evaluation of dam breach

2 基于AHP-BN法的生命损失评价模型

2.1 实施步骤

2.1.1 AHP计算权重

AHP是一种定性和定量相结合，系统化、层次化的分析方法,在处理复杂的决策问题上具有实用性和有效性[16]。利用层次分析法计算图1模型各指标权重，大致步骤如下：①构造判断矩阵；②层次单排序及一致性检验；③层次总排序及一致性检验。

2.1.2 BN计算概率

BN又称信度网络，是目前不确定知识表达和推理领域最有效的理论模型之一，是一种概率图模型，由Pear首先提出[17]。贝叶斯网络由有向无环图(directed acyclic graph，DAG)和条件概率表集(condition probability table，CPT)组成，如图2所示，其中节点X、Y为节点Z的父节点，节点Z为节点X、Y的子节点，它们之间用有向线段连接。

图2 贝叶斯网络示意图Figure 2 Schematic diagram of Bayesian network

贝叶斯网络的理论依据是贝叶斯公式和全概率公式，如式(1)和式(2)所示：

(1)

(2)

式中：P(B)为事件B发生的概率，为先验概率，即在完全不考虑其他因素情况下事件B的概率；P(B|A)表示事件A已发生，事件A发生是由事件B发生引起的概率，为后验概率；P(A|B)为似然率；i为事件个数。

由式(1)和式(2)可知，通过给定所有节点的先验概率及每个节点的条件概率表集，即可得到包含所有节点的联合概率分布，如式(3)所示：

P(A,B,C)=P(C|A,B)P(A,B)=

P(C|A,B)P(A)P(B)。

(3)

2.1.3 计算风险值

利用AHP计算出指标的权重W，BN计算出指标的概率P，根据式(4)可计算出溃坝生命损失风险值R[18-19]：

R=W(A)×P(A)+W(B)×P(B)+

W(C)×P(C)。

(4)

2.2 专家评分标准

为便于专家参考和打分，保证评价结果的科学性，需明确专家打分的标准。

2.2.1 权重打分标准

利用AHP构建判断矩阵计算指标权重时，打分可根据文献[20]中具有较好认可度的9级赋值法，如表1所示。

表1 aij取值及意义Table 1 Value and significance of aij

2.2.2 概率打分标准

贝叶斯网络的条件概率可结合联合国政府间气候变化专门委员会(Intergovernmental Panel on Climate Change，IPCC)机构提出的概率定性表述，划分为7级[21]，如表2所示。

表2 概率定性表述Table 2 Probability qualitative statement

一些指标(例如警报时间)其先验概率打分标准值可根据相应的阈值进行插值计算，一些定性的指标打分标准(例如溃坝理解程度)可在专家经验和工程实际的基础上人工确定。根据相关资料[22]，将洪水严重性程度、风险人口、警报时间、青壮年比例、救援能力、建筑物质量划分为3个等级，相应打分参考见表3；将溃坝理解程度、溃坝发生时间划分为2个等级，相应打分参考见表4。

表3 三等级专家打分参考值Table 3 Reference values of three-level index expert scoring

表4 二等级专家打分参考值Table 4 Reference values of two-level index expert scoring

3 实例验证

将评价模型应用于国内3座已溃大坝中，使用层次分析法对各级指标的权重赋值见表5。

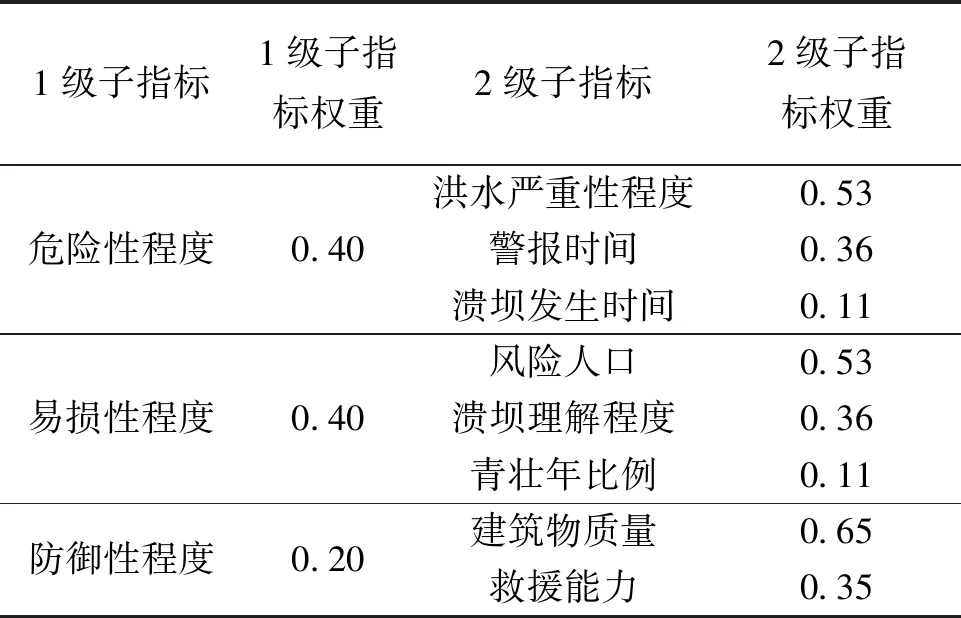
表5 各级指标权重计算结果Table 5 Weight calculation results of indicators at all levels

根据3座大坝的资料对贝叶斯网络先验概率进行赋值，3座大坝溃坝相关信息见表6[22]。

表6 大坝基本情况Table 6 Basic condition of dams

根据表2对条件概率值打分拟定，使用贝叶斯网络，最终计算出每座大坝2级指标的概率值，结果见表7。

表7 2级指标概率值计算结果Table 7 Probability calculation results of indicators at secondary level

根据式(4)运用AHP-BN法，计算出大坝的风险值R，结果见表8。

表8 风险值计算结果Table 8 Calculation results of risk value

3座大坝实际生命损失情况为：李家咀516人、洞口庙186人和史家沟81人。根据表8计算结果可知，3座大坝的溃坝生命损失风险值R从大到小依次为李家咀、洞口庙和史家沟，与实际生命损失大小排序相一致，验证了方法的可行性。

4 结论

溃坝生命损失评价是有效判定水库大坝风险水平的重要方面。针对现有溃坝生命损失评价方法不适用于大量大坝的溃坝后果评价的状况，提出一种适用于大量大坝生命损失风险评价的模型。利用AHP-BN法不仅能解决不确定问题，而且能综合考虑要素权重和要素发生概率，减少评价主观性，对溃坝生命损失风险进行评价。将模型应用于实例，3座大坝风险值从大到小依次为李家咀、洞口庙和史家沟，结果与实际情况相一致，验证了模型良好的有效性，可为预案编制和针对性应急措施的制定提供借鉴和指导，具有一定的工程应用价值。