基于时差和多普勒频率的双发单收目标定位系统性能分析
秦 永,邬 赟,魏朝平,谭文群,樊飞燕
(南昌工程学院 江西省水信息协同感知与智能处理重点实验室,江西 南昌 330099)
目标定位是利用电磁波探测目标后获得某个测量参数来对目标位置等信息进行解算的过程,根据电磁波的获得方式不同定位算法可分为有源和无源定位两种。其中有源定位是雷达发射机主动发射电磁波探测目标,其在战场上容易被敌方监测并被反辐射导弹摧毁[1-2]。而无源定位系统中的雷达接收机不发射电磁波,其具有隐蔽性强不易被发现的优点,因此此类定位系统已成为近些年的研究热点。在无源定位系统中,根据雷达接收机获得的不同参数,定位方法可分为方位角定位[3]、时差定位[4]、多普勒频率定位[5]以及利用两种以上参数的联合定位[6-8]算法。由于时间差定位只与目标和接收站的位置信息相关,其定位解算方法简单并且接收机获得的时间差误差小,因此在目标定位过程此类方法选用的较多。但时间差定位需要同时有三个以上的观测站获得信息,并且时差定位不能对目标运动速度信息进行估计,即存在速度模糊现象。文献[9]基于两站提出了一种仅用时间差信息对目标定位的算法,该算法没有对目标速度估计性能进行分析,并且假设目标需要长时间匀速运动。文献[10]提出了一种唯多普勒信息的目标定位算法,该算法同时对目标位置和速度信息进行了估计,但其在发射站数为4个以上时估计精度才能有效提高,并且该算法同样假设目标长时间内保持匀速运动。可见,仅采用时间差或者多普勒信息对目标位置和速度信息进行估计存在比较明显的局限性,因此利用时间差和多普勒信息对目标进行联合定位算法成为了定位算法的研究热点之一。
本文主要研究基于两个非合作发射站一个接收站-双发单收无源定位系统的时间差和多普勒频率联合定位算法。利用多个观测时间的数据进行联合定位,以提高目标定位的精度。其中多普勒频率为电磁波探测到目标的散射波相对于直达波的偏移,时间差是直达波和反射波的时间差。通过二维定位的方式研究时间差和多普勒频率误差及观测时间对目标位置和运动信息估计的性能的影响。
1 定位模型
1.1 时间差定位模型
假设在二维空间存在两个非合作的发射站其坐标分别表示为(x1,y1)和(x2,y2),接收站坐标为(xR,yR)。目标T(xk,yk)在短时间内做匀速直线运动,其速度为(vx,vy),观测间隔为Δt。定位模型如图1所示。
由图1可知,时间差定位方程只与目标及各站点位置有关,时间差定位方程可表示为
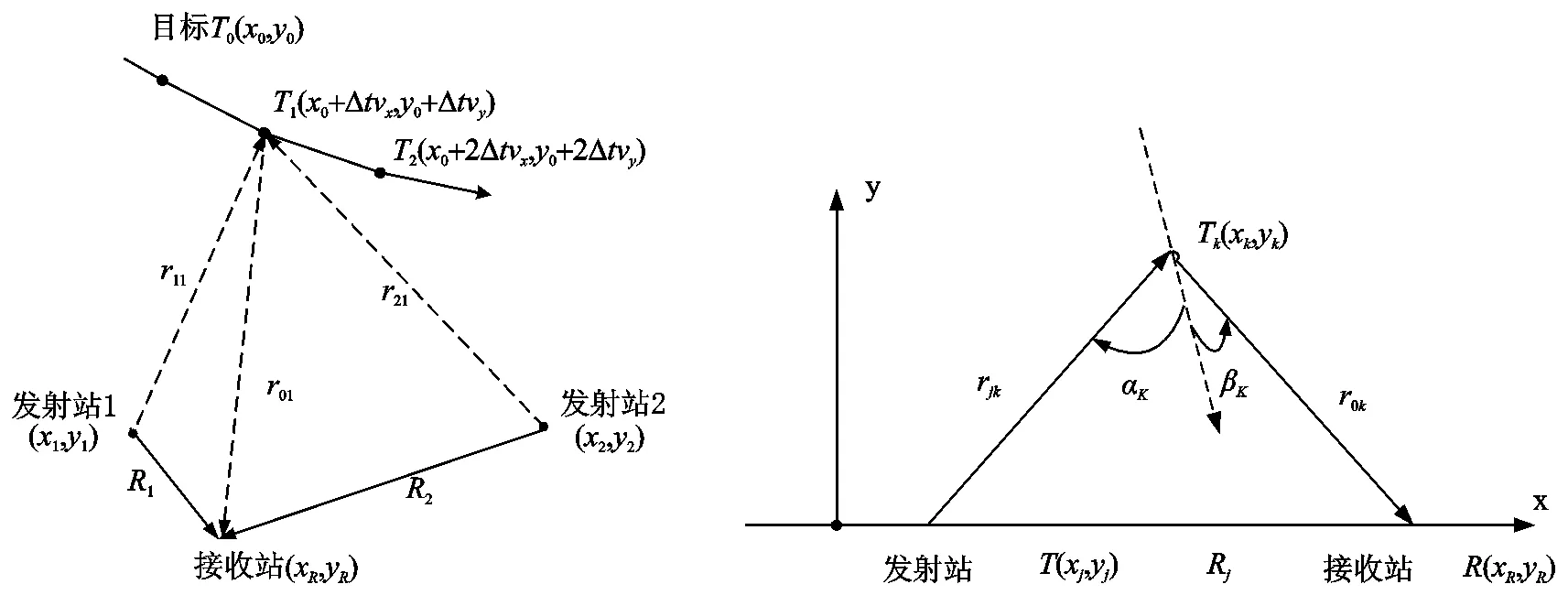
图1 时差定位模型 图2 多普勒定位模型
(1)
其中τk为第j个发射站的时间差,rk1为目标到发射站j的距离,r01为目标到接收站的距离,Rj为发射站到接收站的距离,c为光速。
(2)
假设目标初始位置矢量为X0=[x0,y0,vx,vy],其中[x0,y0]表示目标的初始位置,由于目标短时间内为匀速运动,则在第k时刻目标位置可表示为
xk=x0+kΔtvx,yk=y0+kΔtvy.
(3)
该系统有2个发射站,因此一个时间点可以获得两个时差方程。当使用k个观测点进行定位时可以获得2k个时差方程,因此利用多个观测时间点对目标进行定位其相当于一个跟踪过程。
1.2 多普勒定位模型
当目标高速运动时,目标与接收机的相对运动所产生的频率与发射站相对运动产频率会产生偏差,这个偏差就是多普勒频率。发射站和接收站多普勒频率测量模型如图2所示。
多普勒测量方程如下:
(4)
其中fk为多普勒频率,f为发射站频率,αk为相对目标运动方向的入射角,βk为相对目标运动方向的散射角,v为目标运动速度。利用发射站、接收站及目标位置信息上式可改写为
(5)
本文研究的系统为双发单收的无源定位系统,因此利用式(1)和式(3)可构建一组时差多普勒联合定位方程,二维定位过程中只需要来自两个发射站的联合定位方程即可对目标的位置和速度信息进行定位解算。当利用k个观测时刻对目标进行定位时,可以获得多组时差—多普勒定位方程。
2 时间差多普勒定位精度分析原理
本文研究的双发单收无源定位系统,采用时间差多普勒联合定位方法。为了提高定位的精度可以采用多次观测数据对目标进行定位,此过程相当于一个跟踪过程。衡量定位精度常采用基于克拉美罗界(CRLB)的定位精度几何稀释(GDOP)来评价定位整体误差。下面给出双发单收无源定位系统时间差多普勒联合定位的GDOP表达式。
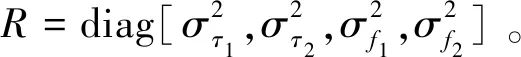
(6)
其中
(7)
利用时差和多普勒表达式,通过计算可得到:
(8)
(9)
(10)
(11)
(12)
(13)
(14)
(15)
其次利用雅克比矩阵表达式,得到联合定位Fisher信息矩阵:
(16)
利用Fisher信息矩阵可以获得时间差多普勒联合定位的CRLB:
(17)
GDOP是描述整个观测空间每个定位点状态估计的CRLB,因此可知
GDOP={Tr(C)}1/2
(18)
最后根据与GDOP与CRLB的关系可以获得:
(1)联合定位位置估计的PDOP(Position DOP)的表达式为:
PDOP=[CRLB(1,1)+CRLB(2,2)]1/2.
(19)
(2)联合定位速度估计的VDOP(Velocity DOP)表达式为:
VDOP=[CRLB(3,3)+CRLB(4,4)]1/2.
(20)
上面给出的是一个接收站在一个观测时间的GDOP表达式,在实际应用中随着观测点的增加其定位精度也会不同。下面仿真将从不同观测时间和不同参数误差方面来分析时间差多普勒联合定位对目标位置信息和速度信息的精度影响。
3 算法仿真
下面将对双发单收无源定位系统时差多普勒定位算法性能进行仿真分析,假设两个发射站为民用的AM短波电台,此类电台可以通过电离层传播且全天候工作,非常适合无源定位系统。假设观测区域为100×100km,两个AM短波电台位置分别为(-15,-15)km和(15,-15)km,发射频率分别为16.5MHz和14.5MHz。接收站位置为(0,20)km。目标短时间内做匀速直线运动,运动速度为(300cos 60°,300sin 60°)m/s即飞行速度为300m/s,飞行高度为3 km,观测时间间隔为Δt=1s。下面分两个不同仿真环境进行比较。
(1)利用不同观测时间数据进行定位,观测时刻设为N=1,5;时间差误差标准差为50ns,多普勒频率误差标准差为0.1Hz。
由图3可知当观测时间为N=1,5时,时间差和多普勒频率联合定位算法均能够对目标的位置和速度信息进行有效的估计(PDOP为目标位置定位估计精度,VPOP为目标速度估计精度)。但随着N的增大,无论是是PDOP还是VDOP图的误差等高线图均得到了很大的提高(如图3(a)的PDOP显示位置误差大部分在70m以内,而图3(c)的PDOP显示位置误差大部分在40m以内;相应的VDOP图精度也得到了很大的提高),即目标定位精度得到了有效的提高。这主要是由于随着观测时间N的增加目标定位的信息量越大,其定位相当于一个跟踪过程,因此定位误差相对提高很多。但利用多个观测时间定位其需要目标在这些观测时间内保持匀速直线运动,若目标在此时间内发生机动运动,定位结果也将迅速下降。
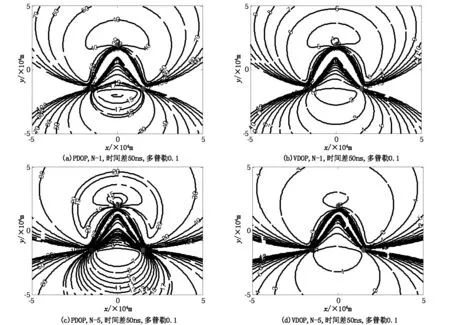
图3 仿真1 GDOP结果
(2)研究时差误差对定位精度的影响,假设观测时刻设为N=2;多普勒频率误差标准差为0.1Hz,时间差误差标准差为100ns和200ns。
图4给出了不同时差误差情况下,目标位置和速度定位精度比较图。图4(a)和图4(c)分别表示两种时差误差下的PDOP误差等高图,其表明联合定位算法的目标位置估计精度随着时差误差的减小而迅速提高。图4(b)和图4(d)为两种情况下的VDOP误差图,这两个图几乎一样,这说明时差误差对目标速度影响不大。

图4 仿真2 GDOP结果
(3)研究多普勒频率误差对定位精度的影响,假设观测时刻设为N=2;时间差误差标准差为50ns,多普勒频率误差标准差为0.1Hz0.05Hz。
由图4可知,图5(b)和图5(d)分别表示两种不同多普勒频率误差情况下的VDOP误差等高图,其表明联合定位算法的速度估计精度随着多普勒频率误差的减小而迅速提高。图5(a)和图5(c)分别表示两种不同多普勒频率误差情况下的PDOP误差等高图,这两个图的误差等高线几乎一样,这说明时间差和多普勒联合定位过程中位置信息的精度主要由时间差误差决定,与多普勒频率误差关系不大。即多普勒误差只对定位的速度信息有明显影响,而对位置信息影响不大。
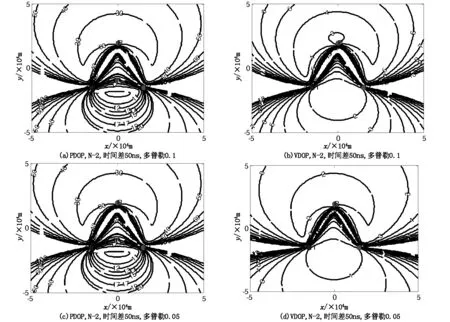
图5 仿真3 GDOP结果
4 结论
本文对双发单收的无源定位系统进行了研究,其中主要研究了时间差多普勒频率联合定位的原理及误差评价方法,最终对该联合定位算法的性能进行了系统性的分析。仿真实验表明时间差多普勒联合定位方法可以利用多个观测点的信息对目标的位置和速度信息进行有效的估计,该估计过程可以看成是一个目标定位过程。

