考虑桥梁结构运动的河口大跨桥梁事故风险因素分析

李骁楠，陈 丰，董博文

（1.同济大学道路与交通工程教育部重点实验室，上海201804；2.上海市政工程设计研究总院（集团）有限公司，上海200092）

河口大跨桥梁是指位于大型河流入海口区域、以实现两岸跨海运输为主要目的的大跨径桥梁，作为连接沿海地区各中心城市的重要运输通道，此类大桥对减少公路运输里程、加强区域合作交流、缓解湾区城市拥堵以及促进区域经济发展起到了极大的推动作用。然而，由于复杂多变的天气、桥梁自身的结构变化和日益增长的交通量等原因，河口区域大跨桥梁相较于普通道路，往往成为交通事故的重灾区，且应急救援难度大，容易造成较大的人员伤亡和财产损失。2020年5月，广东虎门大桥因桥面振幅过大影响行车舒适性和交通安全，紧急封闭，导致广州绕城高速几乎全线拥堵。由此可见，结合桥梁结构振动数据、气象数据、交通流数据和事故数据，探究河口大跨桥梁的事故风险因素具有极其重要的意义。

近年来，国内外学者致力于探究各类风险因素对交通事故的影响机理，侧重点各有不同。基于多源数据的事故分析研究方面，Yu等［1］利用分级贝叶斯方法分别研究了线形数据、实时天气数据、交通数据对交通事故发生的影响程度。Ahmed等［2］总结了上述多源数据对事故发生可能性的研究结果，采用周期流量、速度、占有率、区间速度、天气（能见度、降雨等）、道路线形（曲率、坡度）的数据结合事故数据对高速公路的风险进行实时评估研究。Chen等［3］基于美国科罗拉多I-25公路的实时短间隔面板数据，采用随机效应托宾模型对道路区间的事故率进行了研究，其数据包括道路线型数据、路段区间天气与路面条件数据、交通流特征数据以及事故数据。随后Chen等［4］又在2016年利用不平衡的面板数据开发了具有特定地点随机效应的零膨胀负二项式模型，对事故频率进行了预测。国内由于数据获取难度较大，在基于多源数据的事故分析方法这一方面的研究成果较少。赵新勇［5］采用支持向量机等方法构建了基于交通流参数的高速公路风险判别模型，融合天气、驾驶员特性、道路参数等因素，探究其对公路行车安全的影响。杨曼等［6］用K-均值聚类分析法对驾驶风险进行分类，运用Logit模型分析天气、车速、驾驶员年龄和驾龄对驾驶风险的影响程度。马聪等［7］从道路线形和环境条件2个方面选取13个自变量，分别采用负二项回归模型和非线性负二项回归模型建立了交通事故起数预测模型，分析显著自变量对交通事故起数的影响程度。曾强等［8］采集了高速公路的事故、道路、交通和气象数据，采用时空交互模型拟合路段季节事故数和道路设计参数、交通特征、气象因素间的内在关系。

在大桥交通事故特点及成因分析方面，国外Murthy等［9］采用模糊集的方法建立了桥梁交通安全评估模型，从桥梁设计、进口设计、环境因素3个方面选取基础指标对印第安纳州的多座桥梁进行宏观建模，寻找潜在的交通安全风险因素。Gates等［10］使用logistic回归和卡方检验的方法对96起发生在高速公路桥梁进口的事故进行研究，分析桥梁进口护栏对于交通事故严重性的影响。Mehta等［11］采用负二项回归方法对阿拉巴马州主要高速公路桥梁的交通事故及桥梁设计参数进行建模，探究最合适的大桥安全性能评估函数。国内黄冰娥等［12］基于长三角地区苏通大桥通车以来的交通事故资料，采用描述性统计方法对其事故的时空分布、事故形态、车辆类型、天气状况等多角度进行了研究。王文治等［13］整理了杭州湾大桥3年的交通事故，采用图表及相关性的统计方法，从时空分布、事故类型和天气状况等方面对其特征进行分析。

在国内外现有研究中，使用多源数据进行交通事故致因分析的研究成果大多集中于道路段，很少涉及桥梁路段。研究的数据内容主要集中在气象信息、道路线形设计和驾驶员行为数据，缺乏对桥梁结构运动数据的考虑和研究。而国内外关于大桥行车安全问题的研究中，大多采用描述性统计方法，影响因素选用时间、空间和天气情况，未考虑桥面结构运动等因素，无法体现大桥行车问题的特殊性。针对上述问题，本文以河口区域大型桥梁为研究对象，基于大桥健康监测系统提供的多源实时数据，考虑桥梁结构运动，首先处理原始数据，然后运用时间对应匹配和随机抽样匹配2种方法抽取数据集，检验单车与多车事故差异性，建立条件logistic回归模型，分析影响大桥行车安全的事故风险因素。

1 数据采集与处理

1.1 数据来源

嘉绍大桥位于中国浙江省杭州湾海域内，是国家高速G1522的组成部分。嘉绍大桥是一座典型的河口大跨桥梁，是跨越钱塘江入海口的关键性工程，全长10.137 km，桥面宽40.5 m，双向8车道，设计速度为100 km·h-1。嘉绍大桥安装了完善的传感器设备，可以实时记录气象、交通流、结构、事故信息等各类关键数据。获取了嘉绍大桥2013年7月15日至2017年12月31日的多源实时数据，其中，气象、结构和交通流数据由桥上安装的多个传感器采集，事故信息采集由后期人工查阅监控视频完成。

1.2 数据结构

1.2.1 气象数据

嘉绍大桥的气象数据包括风速、温度、湿度、降雨4项内容，设备记录的数据类型为：竖直风速、综合风速、竖直风向、水平风速和水平风向。考虑到气象状态在10 km范围内的差异性不大，以布置在跨中的气象监测点数据近似代表全桥的气象状态。温度和湿度以10 min为间隔求平均值，降雨数据转化为虚拟变量，10 min内有降雨，则表示为1，否则为0。以往的研究表明，横风是造成侧翻等交通事故的重要原因，为提高模型效率，单独提取大桥横向风速作为模型的解释变量。由于风速仪没有直接记录大桥横向风速，根据实测数据计算公式如下：

式中：Vc_w为大桥横向风速；Vh为大桥水平风速；Dh为大桥水平风向。计算10 min平均纵向风速、10 min平均横向风速和10 min内最大综合风速作为解释变量。

1.2.2 交通数据

嘉绍大桥布设了一套8车道动态称重系统，系统可记录每一辆车通过时的车道、方向、速度、轴数、车型、重量等各项数据，据此可计算单位时间内通过该截面的车流量、平均通行速度和货车比例（货车比例是指单位时间内通过该截面货车数量与总车辆数之比）。

交通状态可以分为宏观交通状态（较长时间跨度）和微观交通状态（较短时间跨度），为了研究哪一种交通状态会对事故概率产生影响，分别为每一起事故（或非事故）匹配其所处时刻10 min范围内和1 h范围内的交通状态，包括交通流量、平均通行速度和货车比例。

1.2.3 结构数据

嘉绍大桥在主航道桥、北副航道桥和北引桥桥面处均匀布设了16个振动加速度传感器、52个主梁变形监测传感器，记录桥面的横向与纵向振动加速度以及挠度。将每个传感器10 min内最大值作为解释变量。

1.2.4 事故信息

通过人工查阅监控资料发现，自2013年7月通车至2017年8月大桥管辖范围内共发生事故271起，其中致死事故5起，平均每年发生交通事故68起。记录事故发生的日期、时间和距离其最近的桩号。

根据事故发生的时间和桩号，将其与采集得到的多源异构数据进行匹配。对于气象数据和交通数据，均选用事故发生时刻跨中传感器的数据作为该起事故的气象、交通状态。而对于结构数据，选用距离事故最近的传感器数据作为该起事故发生地的结构运动状态。

1.2.5 时间数据

为了体现时间对事故发生率的影响，引入时间相关的虚拟变量，包括季节、工作日或周末、夜晚、白天以及是否是高峰时刻（流量统计表明大桥在每天13：00—16：00为流量高峰期）等，用二进制表示（1表示是，0表示否）。如时间为秋季，则秋季指标为1，否则为0；时间在周四，则工作日指标为1，周末指标为0。

1.3 单车与多车事故的差异性检验

以往的研究表明，对于长距离高速公路，单车事故和多车事故可能存在不同的事故机理，应该分开进行建模［14-15］。但河口大跨桥梁的流量大、长度短且空间狭窄，单、多车事故的影响因素可能没有明显的差异。为了探究单、多车事故的影响因素是否存在显著差异，对单车、多车事故的影响因素分别进行描述性统计，并采用Z检验方法对每个影响因素进行差异性检验。

Z检验，又称曼-惠特尼秩和检验，在Z统计量计算完成后，比较计算所得Z值与理论Z值，并计算与之对应的显著性指标Pr值，依据Z值与差异显著性关系表作出判断，取95%置信区间，若Pr值小于0.05，则拒绝原假设，判断该影响因素存在显著性差异，若Pr值大于0.05，则无法拒绝原假设，判断该影响因素不存在显著性差异。

计算所有单、多车影响因素的Z统计量及对应的Pr值。单、多车事故影响因素的描述性统计及Z检验结果如表1所示。

如表1所示，Z检验的Pr值代表了单、多车事故影响因素的差异性水平，计算结果表明，所有单、多车事故的影响因素均没有显著性差异（Pr值均大于0.05），可以判断，对于嘉绍大桥，单车和多车事故的潜在风险因素没有显著的差异。此外，由于研究中事故数过少，导致模型样本量小，如果将单、多车事故分开建模，可能会因样本量不足导致模型准确性下降。基于上述原因，将所有事故共同建模，不再区分单、多车事故。

2 模型选择与建立

2.1 模型选择

由于大桥道路多为直线段，线形设计参数没有显著的变化特征，为了控制路段本身线形因素对事故的影响，为每个事故段匹配相同位置的非事故段，近似于分层匹配对照问题。条件logistic模型相比于传统logistic模型，其优势在于，能够控制无关变量，从而研究其他变量对结果的显著性影响。

将“路段”作为控制条件，运用条件logistic模型，研究其他因素对大桥交通事故发生概率的影响，条件logistic模型原理如下：

假设共有N起事故，令发生在同一地点的每一起事故和与其匹配的m起非事故都属于一个单独的一层j，j=1，2，3…，N。那么第j层的条件概率即为在给定总体观测和事故观测情况下，该层观测数据的可能性。令pj(Xij)为第i个观测在第j层发生事故的可能性，Xij=(x1ij，x2ij，...，xkij)即为该观测k个解释变量的向量，这里i=0，1，2，…，m，j=1，2，…，N。因此事故发生可能性pj(Xij)可以用一个线性logistic方程表达为

式中：aj为截距项；β1，β2，...，βk为每一个解释变量的系数。

为了计算上述方程中的系数，定义条件似然值。该似然值由N项构成，每一项都是第j层中m+1个观测的事故发生概率之和。经过推导，最终的条件似然函数可以表示为如下形式：

可以发现，条件似然值L(β)与截距项aj是相互独立的，因此每一层的截距项是无法估计的，式（2）也不能用于计算每一层事故发生的概率。但从式中可知，通过最大化似然函数L(β)得到的系数β与式（2）中的β是相同的，因此这些系数可以用于计算优势比，从而得到事故影响因素的相对风险。

2.2 抽样对照法建立数据集

由于道路交通事故属于“罕见事件”，交通事故数据量远低于非事故数据量，选择抽样对照研究法，以已发生交通事故的路段和时间段作为病例组，通常以1：5的比例随机选取未发生交通事故的路段和时间段作为对照组，从而保证样本的平衡性。

对于大跨桥梁交通安全研究而言，抽样对照研究有如下优点：①能够控制某些难以观测变量的影响。在交通安全研究中，很多因素无法观测，如路段本身带来的未观测异质性，对照研究可以在匹配时为每个事故段选择位置相同的非事故段，从而控制路段因素的影响，减少误差；②能够控制事故与非事故数据的比例在合理范围内，增加数据的平衡性和模型的可靠度。

对于每一个事故时段，匹配4起与其处于相同位置的非事故时段，存在2种匹配方式：一是时间对应匹配方法，即对每一个事故时间段，匹配与其独立（不在同1天之内）但是处于相同时刻的非事故时间段；二是随机抽样匹配方法，即对每一个事故时间段，随机匹配与其独立（不在同1天之内）的非事故时间段。

时间对应匹配法与随机抽样匹配法各有优劣。时间对应匹配方法选用前后2周的同1天进行匹配，可以控制时间因素（如星期、驾驶员不同时刻生理状态等）的影响，但由于大桥的气象和交通状态与时间有着较高的相关性，很容易在控制时间因素的同时也控制了气象和交通因素。而随机抽样匹配方法仅控制地形因素的影响，不存在上述问题，但是由于采用随机抽样方式，容易因抽样问题导致统计结果存在偏差。

由于上述2种方法各有优缺点，针对2种方法匹配的数据集分别进行建模，对比分析。为了避免随机抽样匹配方法因抽样问题导致的统计偏差，建立5个不同的随机抽样匹配数据集，对其计算结果进行综合评价分析。

3 结果与分析

3.1 模型结果

采用条件logistic模型对病例对照数据集进行建模，研究使用后向选择法对显著变量进行筛选，在使用后向选择法进行变量筛选的过程中，有些以不同时间尺度记录的同一指标会出现较高的相关性（如10min流量和小时流量），因此只选择两者中显著性较高的变量进入最终模型。

时间对应匹配方法和随机抽样匹配方法的结果分别如表2和表3-7所示，表中A表示10min流量值，模型的ROC曲线如图1所示。

图1 病例对照模型ROC曲线Fig.1 ROC curve of Case Control Models

表2 时间匹配方法模型预估结果Tab.2 Prediction results of time matching method model

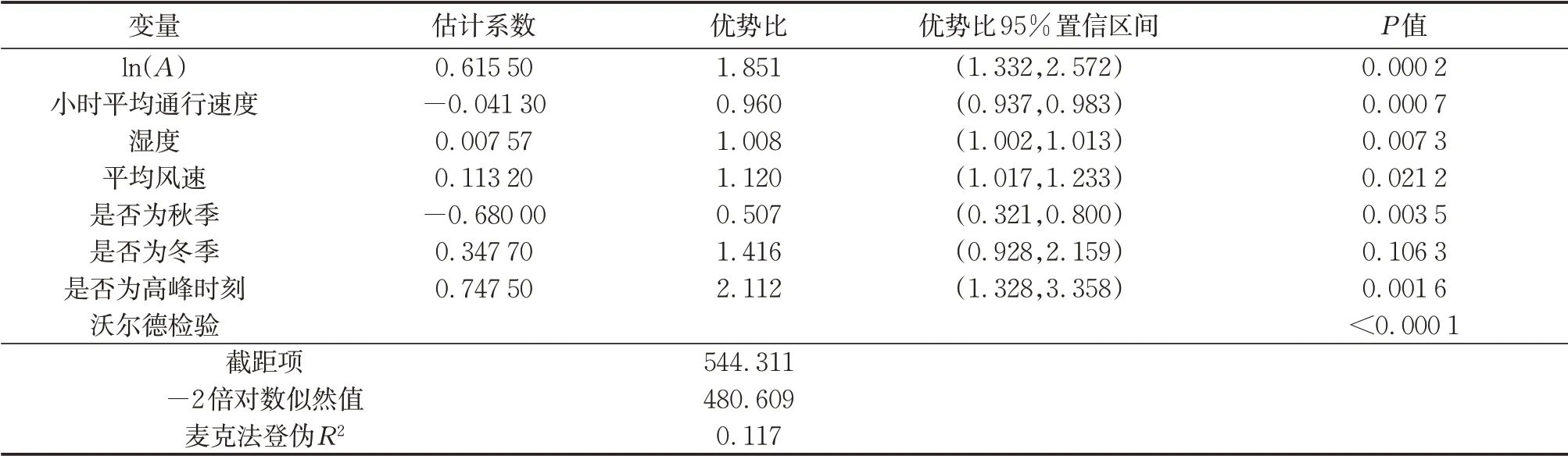
表3 随机抽样集1模型预估结果Tab.3 Prediction results of Random Sampling Set 1 Model

表4 随机抽样集2模型预估结果Tab.4 Prediction results of Random Sampling Set 2 Model

表5 随机抽样集3模型预估结果Tab.5 Prediction results of Random Sampling Set 3 Model

选用似然比检验和作为模型是否整体显著的评判标准，参考以往研究，选用麦克法登伪R2和AUC值作为模型拟合精度的评判标准［16］。从统计结果可以看出，所有模型均通过似然比检验，说明模型中选用的指标与大桥事故发生的概率有显著的相关性。

表6 随机抽样集4模型预估结果Tab.6 Prediction results of Random Sampling Set 4 Model

表7 随机抽样集5模型预估结果Tab.7 Prediction results of Random Sampling Set 5 Model

对比表2和表3-7可知，随机抽样匹配方法得到的显著变量要多于时间对应匹配方法，且其拟合精度AUC值略高于时间对应匹配方法，麦克法登伪R2也远高于时间对应匹配方法，说明确实存在前文讨论的模型偏差，即时间对应匹配方法在控制时间因素的同时也控制了其他可能的显著风险因素。综合对比，选用随机抽样匹配方法作为病例对照模型的主要匹配方法。

通过对比5个随机抽样匹配数据集的建模结果发现，所有随机抽样模型的麦克法登伪R2和AUC值均相差不大。虽然模型的拟合精度相差不大，但是对不同的随机抽样集建模会得出不同的显著风险因素，有的变量在所有结果中都显著，而有的变量只在个别结果中显著。这说明随机抽样方法确实会对统计结果造成影响，也说明研究中选取的指标有着不同的影响程度。因此，为了能够更准确地对大桥交通安全风险因素进行评价，需要对比所有随机抽样统计结果，做出综合评判。

3.2 事故因素分析

3.2.1 交通因素

由表3-7可知，所有统计结果都表明10 min流量和小时平均通行速度是影响事故发生可能的显著变量。实际上，从后向选择过程来看，上述2个变量分别对应的小时流量和10 min通行速度也显示出了很高的显著性水平。这说明流量和平均通行速度会对事故发生概率带来显著的影响，从模型的估计系数可知，流量越大，事故发生的概率越大，而平均通行速度越大，事故发生的概率越小，这与大多数研究结果一致［1，3-4，8，11，13-14，17］。

由于模型的抽样样本不同，优势比的结果也有差异，这里以拟合效果最好的随机抽样集1为例，分析其优势比计算结果。

如表3所示，10 min流量（ln值）的优势比为1.851，当10 min流量的自然对数值提高1时，发生事故的概率比之前提高85%。例如，当10 min车流量的由100辆（自然对数值4.6）提高到270辆（自然对数值5.6）时，发生事故的概率会提高85%，这与曾强等［8］得到的结论一致，即交通量与事故频次是非线性正相关的关系。小时平均通行速度的优势比为0.96，当小时平均通行速度的增加1 km·h-1时，发生事故的概率是之前的96%，与Yu等［1］在其研究中得出的结论一致，车辆车速偏低时，走走停停的状态更容易导致碰撞发生。在5个随机抽样建模结果中，10min流量和小时平均通行速度的优势比相差不大，说明计算结果有较高的可靠度。

从结果来看，货车比例对于大桥交通事故的发生概率没有显著影响，这与已有研究结论不同。以往研究认为，货车比例对事故发生率产生负影响，即货车占比越大，事故发生率越低，对此学者们认为货车司机通常驾驶技术更好、对驾驶路线熟悉程度更高，因此驾驶行为更安全［8，17］；也有一些观点认为货车比例仅与多车碰撞事故发生率负相关，而与单车碰撞事故发生率正相关，因为单车碰撞通常包括侧翻，这类事故更容易发生在卡车身上［11］。本文得出的结论为货车比例对大桥事故发生率无显著影响，可以参考张诗雯等［18］关于自由流条件下货车比例对交通安全的影响研究，该研究指出，货车比例在0.15至0.50之间时，交通状态较安全，安全系数随货车比例增加而减少，当货车比例在0.35至0.50之间时，安全系数曲线趋近于一条斜率为零的直线段。由本研究的观察原始数据可知，嘉绍大桥的货车比例约在0.30至0.50之间，与张诗雯等［18］研究结果一致。

3.2.2 气象因素

综合分析5个随机抽样集的模型计算结果可知，湿度在3个抽样集中都表现为显著，但显著性不高（0.7左右），说明湿度是一个相对较显著的影响因素，与众多研究结论一致［3-4，6，8，13-14］。根据其估计系数可知，当湿度增加时，车辆轮胎与路面之间的道路附着系数下降，行驶车辆制动效果变差，大桥交通事故发生率增加。该指标的优势比在1.01左右，表明当湿度增加1%时，发生事故的概率比之前提高1%。

3.2.3 时间因素

5个模型的计算结果均表明，秋季是显著的影响因素，其估计系数为负，说明当时间为秋季时，事故发生的概率会降低。在5个模型中，该指标的优势比相差不大，表明秋季的影响较为稳定，仍然以第1个随机抽样集的结果为例，优势比为0.507，说明在秋季时，事故发生的概率是原来的50%。杨曼等［6］针对国内某高速路段研究发现，受节假日影响，10月是事故高发月；而国外针对科罗拉多州高速的若干研究表明［3-4，14］，11月正值科罗拉多州冬季风暴盛行，因此11月是事故高发月。由此可见，月份或季节对事故发生率的影响取决于当地气候和人文环境等复杂因素。嘉绍大桥在秋季事故率较低，可能是因为嘉绍大桥在10月节假日期间管控措施到位，且嘉绍大桥所处位置秋季气候宜人，恶劣天气出现概率低，驾驶员能见度较高。

高峰时刻（流量高峰）也在所有的模型中都表现出了较高的显著性，其估计系数为正，这进一步说明了大流量对于交通安全的不利影响。该指标的优势比在2.0～2.6之间，表明当大桥处于流量的高峰时刻时，发生事故的概率是非高峰时刻的2.0～2.6倍。因此，十分有必要做好大桥在高峰时期的安全管控措施和事故预防工作。

3.2.4 结构因素

结构振动也是导致大桥交通事故发生的可能因素，在模型中加入了最能够体现大桥结构运动的主梁形变（挠度）以及横、纵向振动加速度3个变量。基于病例对照的多组模型结果发现，这3个指标均表现为不显著，可以初步说明大桥在合理范围内的振动不会显著导致交通事故率增加，或者表明，在多因素的共同影响作用下，大桥运动对交通事故产生的影响没有其他因素（如交通流、气候、时间等）对交通事故的影响显著。

3.2.5 小结

从交通因素、气象因素、时间因素和结构因素4个角度，依据5个随机抽样集的模型结果，对嘉绍大桥事故致因进行分析，并与已有研究成果进行比较讨论。结果表明，对事故发生率有显著影响的因素有：交通流量、平均通行速度、湿度、秋季、高峰时刻。其中，交通流量、湿度、高峰时刻与事故发生率正相关，平均通行速度和秋季与事故发生率负相关。除秋季事故发生率低与地域特色有关，其余结论均与大多数研究结果一致。

研究表明，货车比例、主梁形变（挠度）以及横、纵向振动加速度对于大桥交通事故的发生概率没有显著影响。

3.3 应对策略

针对上述结论，提出如下大桥管理建议：①在交通流量大、平均通行速度大的事故高发时段采取限流或限速手段，在交通流量大、平均通行速度大的局部路段设置警示类或限制类信息提示牌；②湿度增加1%时，发生事故的概率比之前提高1%，根据历史数据，大桥同一位置检测到的湿度值1h内可能会提升40%，相应的，发生事故的概率将提升40%，因此大桥管理处应设置湿度检测器，时刻关注湿度变化，在湿度较大或湿度提升较快的时段发布安全提示信息；③研究表明，当大桥处于流量的高峰时刻时，发生事故的概率是非高峰时刻的2.0～2.6倍，建议结合大桥自身运营特性，制定高峰期交通管控措施规章；④信息发布方式多元化，例如使用固定或可变信息标志牌、通过互联网发送提示信息至手机App、交通广播等方式全方位地提醒大桥交通参与者注意交通安全；⑤定期养护路面，恢复路面抗滑性能，防止湿度增加时大桥路面道路附着系数下降不利于车辆制动的情况，例如采用微表处、薄层罩面、雾封层、稀浆封层等路面处理方式；⑥充分利用多源数据采集设备，建立与加强对事故多发时段的长效安全预警管理机制，提升大桥智能化、信息化管理水平。

4 结语

为降低河口大跨桥梁的事故率、提升通行效率、减少事故造成的人员伤亡和财产损失，基于大桥健康监测系统提供的多源实时数据，分别采用时间匹配法和随机抽样法抽取数据集，建立条件logistic回归模型，研究气象、交通和大桥结构数据对河口大跨桥梁行车安全的影响。通过建立多个随机抽样回归模型，得到结论如下：①与时间匹配抽样方法相比，随机抽样方法能避免时间因素与气象、交通因素相关性过高的问题，更好地体现气象和交通因素对事故发生率的影响作用，具有更高的拟合精度；②交通流量是大桥交通事故概率的显著正影响因素，而平均通行速度是大桥交通事故概率的显著负影响因素，货车比例对交通事故概率影响不显著；③当湿度增加时，车辆轮胎与路面之间的道路附着系数减小，行驶车辆制动效果变差，大桥事故概率会显著增加；④大桥事故可能性在秋季会显著降低；⑤当大桥处于高峰时间时，事故可能性会显著增加；⑥根据现有检测数据分析，相较于气象、交通、时间等因素，大桥的挠度变化和结构振动对事故发生概率无显著影响。本文考虑了桥面结构振动对大桥行车安全的影响，体现了大桥行车安全问题相较于普通道路行车安全问题的特殊性；采用时间匹配法和随机抽样法，针对病例对照数据集建立条件logistic回归模型，为国内外类似河口大跨桥梁的管理优化提供理论基础参考。不足之处在于：研究对象浙江嘉绍大桥是多塔斜拉桥结构，而虎门大桥是悬索桥结构，斜拉桥是超静定结构，一般不会出现过大的形变，而悬索桥是柔性结构，允许出现更大的变形幅度。接下来的研究将围绕如何采集与研究典型悬索桥的桥梁结构振动对交通安全的影响展开。

作者贡献说明：

李骁楠：数据分析、论文撰写。

陈丰：论文审阅、修改及定稿。

董博文：数据采集与处理、论文审阅。