平板表面边界层流态结构的数值模拟

和生泰 兰巍 胡兴军

(吉林大学 汽车仿真与控制国家重点实验室，吉林 长春 130022)

在叶轮机械中叶片表面边界层的转捩会对叶片气动与传热性能产生很大影响。由于层流边界层摩擦阻力小但是易分离，而湍流边界层摩擦阻力大，不易发生分离且传热率高，在航空工业中，出于不同控制目的，有时需要使转捩提前，有时需要推迟转捩。转捩问题一直是流体力学研究的重点和难点。研究边界层从层流到湍流过程中流态结构的演变具有重要理论意义与工程意义。目前国内外关于边界层转捩问题的数值模拟研究总结为以下几种：直接数值模拟(DNS)[1]、大涡模拟(LES)[2]、基于稳定性理论的eN方法[3]、近似经验关系式方法[4]和基于雷诺平均的的转捩模型方法(如γ-Reθt转捩模型)[5]等。

直接数值模拟与大涡模拟精度高但计算耗费太大，且大涡模拟由于其亚格子应力模型的限制，可以模拟分离流转捩过程，但是无法模拟自然转捩与旁路转捩，若用大涡模型进行自然转捩的模拟，需要在边界层中加入初始扰动或者对大涡模型方程进行一定的修改[6- 8]。基于稳定性理论的eN方法与近似经验关系式方法均需要边界层的积分信息，这一非当地变量导致其与现代CFD求解技术不相容，且基于稳定性理论的eN方法仅能预测低湍流度时的自然转捩，无法预测较高湍流度时发生的旁路转捩[9]。其他一系列基于雷诺平均(RANS)的湍流模型在其建立过程中，经验系数与经验关系的确定均以完全发展湍流为基础，因此无法准确捕捉边界层的层流状态以及转捩过程。

Menter在1994年提出了基于湍动能k与比耗散率ω的两方程湍流模型k-ωSST湍流模型[10]，在此基础上Langtry、Menter等[11- 13]提出了完全基于当地变量的γ-Reθt转捩模型(其中γ为湍流间隙因子，Reθt为边界层动量厚度雷诺数)。雷娟棉等[14]采用该转捩模型对高雷诺数范围内圆柱绕流的转捩与尾流进行了研究，研究中体现出了该转捩模型的优越性。董平等[15]的研究表明，压力梯度对平板边界层转捩区间与位置会产生很大影响。陈奕等[16]采用该转捩模型准确预测了平板边界层转捩并得出湍流水平对转捩的影响。鉴于γ-Reθt转捩模型的优越性，本研究采用γ-Reθt转捩模型对平板表面边界层进行了数值模拟，研究了边界层在法向和流向上的发展变化以及壁面粗糙度、来流风速与湍流度、压力梯度等因素对边界层发展的影响。

1 理论基础与计算设置

γ-Reθt转捩模型在湍动能和比耗散率输运方程的基础上增加了间歇因子γ与当地边界层动量厚度雷诺数Reθt两个参数的输运方程，将这两个参数的输运方程以及相关的经验公式与k-ωSST两方程湍流模型相结合，即构成了四方程转捩模型，间歇因子γ与当地边界层动量厚度雷诺数Reθt两个参数的输运方程如下：

(1)

(2)

式中：ρ为流体密度，μ为流体黏度，μt为湍流黏度，t为时间，xj与uj为位移与速度的张量表达形式，Pθt为动量厚度生成项，Pγ与Eγ为间歇因子输运方程的生成项与耗散项，σγ为输运方程模式系数，间隙因子γ为某一点处于湍流状态与处于层流状态的时间的比值，边界层动量厚度θ定义如下：

(3)

其中,ue为边界层外缘速度。

动量厚度雷诺数定义如下：

(4)

式中，υ为流体运动黏度，边界层动量厚度θ反映了边界层的动量损失，而边界层动量厚度雷诺数是用于关联剪切层特性的最方便的雷诺数。

为提高计算精度，采用二阶迎风格式对控制方程的对流项进行离散。准确预测流动现象不仅要求选择适合研究该流动问题的湍流模型，还需要探索制定合适的网格策略。本研究采用图1所示的结构化网格，第一层网格节点的y+值为0.8，y+值为无量纲的壁面距离，定义如下：

图1 网格示意图

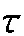
(5)

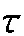
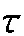
(6)

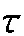
边界层中网格的增长选用Geometric方法，增长率为1.1，节点分布计算方式如下：

(7)

式中，Si为节点与起始位置的距离，R为增长率，N为节点总数。

为了保证计算精度，网格划分时在壁面附近对网格进行加密处理，并在加密与未加密区域设置网格渐变过渡。计算时风速为30 m/s，湍流度为1%，板面粗糙元高度为0，且计算域无压力梯度。

2 边界层的发展变化

不同湍流模型计算的壁面摩擦系数Cf的变化如图2所示。

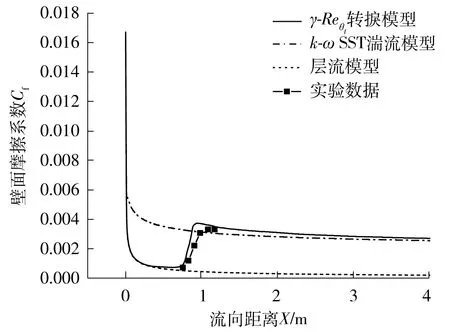
图2 不同湍流模型计算的流向壁面摩擦系数的变化

由图2可见，γ-Reθt转捩模型计算的壁面摩擦系数在距平板前缘0～0.75 m的位置与全层流模型Laminar的计算值基本一致；在距平板前缘0.75～1 m的位置壁面摩擦系数迅速升高，与基于RANS建立的全湍流模型k-ωSST的计算结果基本一致；之后随着流向距离X的增大壁面剪切应力缓慢降低，且趋势与值均与k-ωSST湍流模型一致。这说明在0～0.75 m之间边界层处于层流状态，而在0.75～1 m区间边界层转捩为湍流，转捩过程持续了约0.25 m。S & K平板边界层转捩是典型的自然转捩流动，通常用来考量模型对转捩的模拟能力。由图2所示结果可见，文中采用的转捩模型对转捩区间与位置的预测基本与模型实验结果一致，充分说明了文中仿真策略的预测精度与准确性[17]。其他基于RANS建立的一系列湍流模型计算结果与湍流模型k-ωSST的计算结果基本一致，均无法预测转捩现象，此处不再逐一列出。综上说明层流模型与其他一系列基于RANS建立的全湍流模型均无法预测到边界层的这一转捩现象。

边界层厚度及其增长率的变化如图3所示。

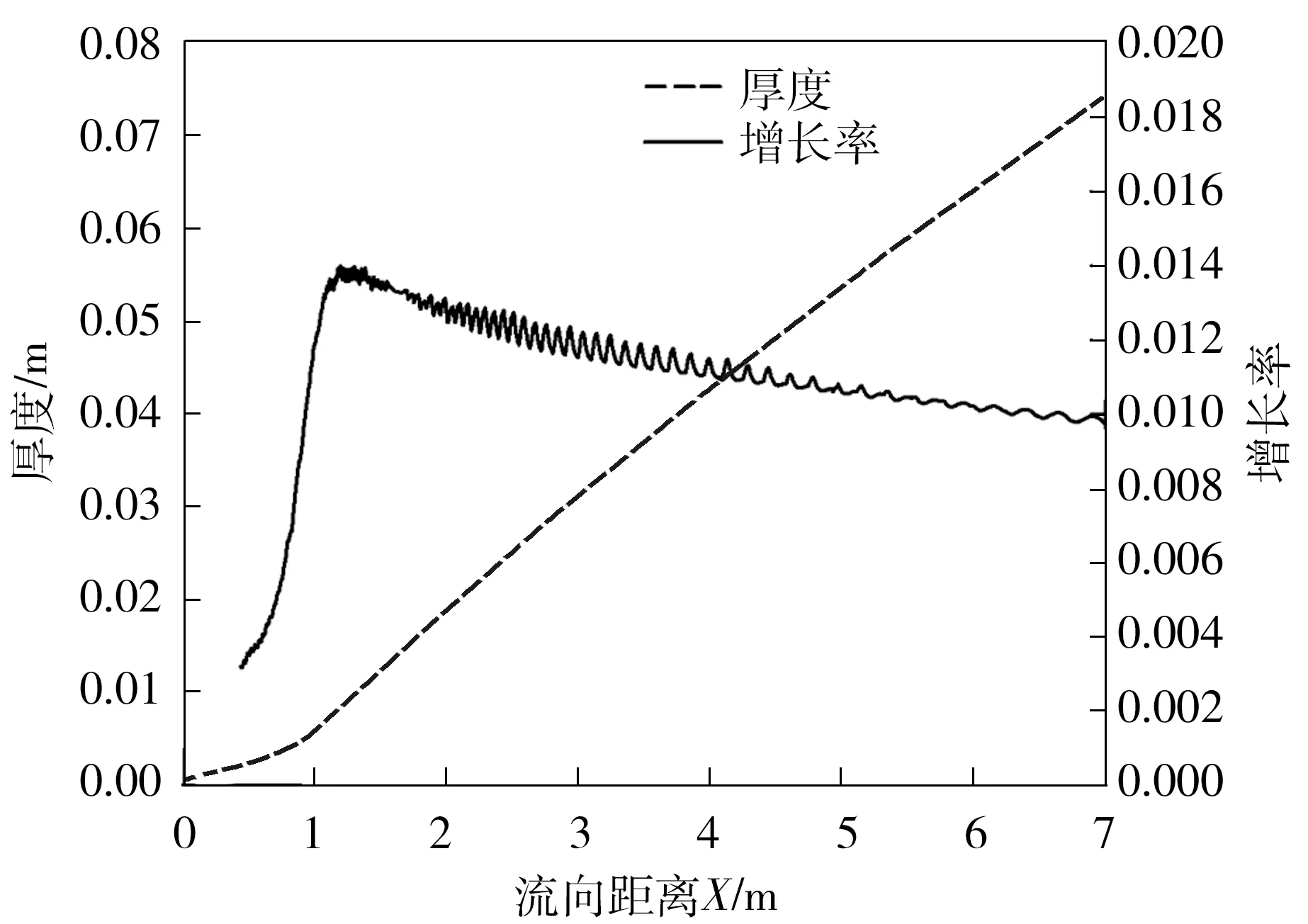
图3 边界层厚度及其增长率的变化

由图3可见，边界层在转捩区间内(即距平板前缘0.75～1 m)时，其增长率突然增大。在转捩后形成的湍流边界层中，虽然其总厚度随流向距离X的增大不断增大，但是其增长率随流向距离X的增大不断减小。

转捩过程中不同流向位置(X)的速度型曲线以及层流与湍流边界层法向速度梯度如图4所示。

由图4(a)可见，转捩过程中法向速度型由层流速度型过渡到了湍流速度型，这两条曲线对应的法向速度梯度如图4(b)所示。由图4(b)可见，在壁面附近约0～0.000 2 m区域(区域1)内湍流边界层的速度梯度远大于层流边界层，因此在该区域内湍流边界层速度远高于层流边界层，且二者的速度差值不断增大，在法向约0.000 2 m处湍流边界层与层流边界层的速度差达到最大，此时二者速度梯度相同；在离壁面的法向距离超过0.000 2 m后湍流边界层速度梯度小于层流边界层(区域2)，之后该速度差开始减小。在离壁面法向距离(Y)约0.000 2 m的高度处(即湍流与层流边界层速度差最大的高度处)总压沿流向的变化如图5所示。由图5可见，由于上述原因导致在转捩过程中该处形成了总压的突变，在其他高度由于速度差值不大所形成的总压变化较小。

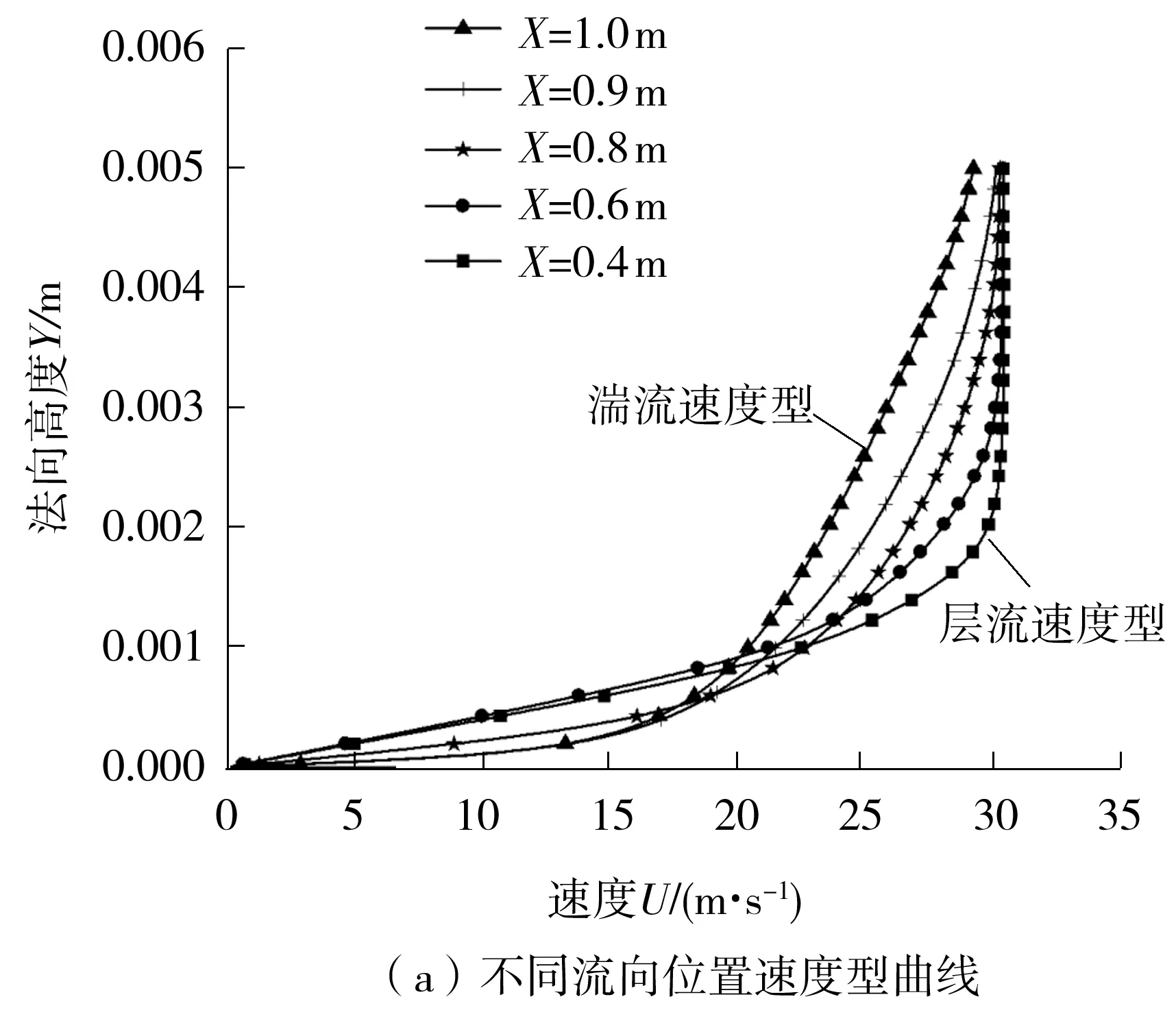
图4 速度型曲线与法向速度梯度

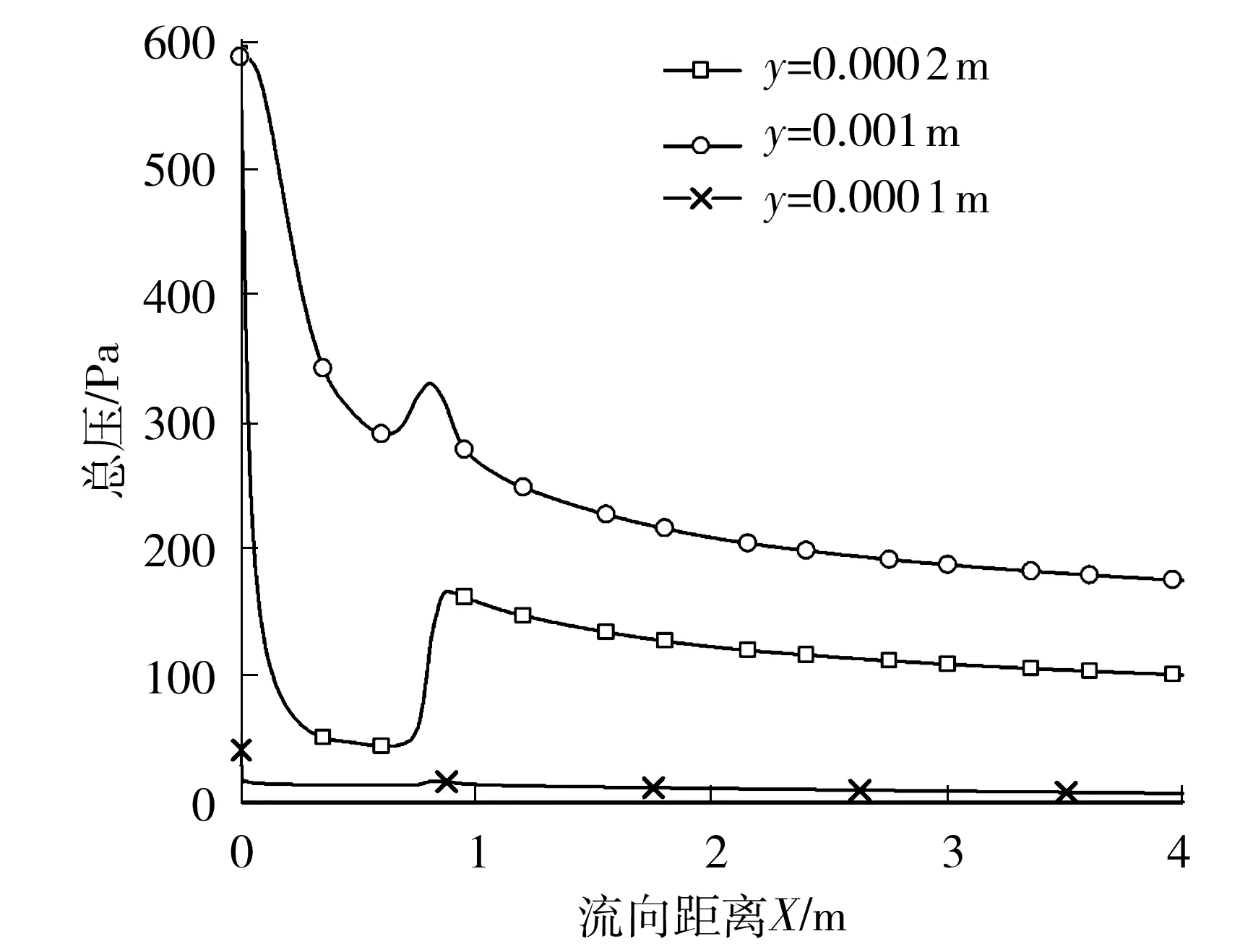
图5 距壁面不同高度的总压沿流向的变化图

对于黏性流体，流体微团所受的表面力为黏应力与雷诺应力。这两种应力有着本质的差别，黏应力对应于分子扩散引起的流体界面两侧的动量交换，而分子的扩散是由分子的热运动引起的。雷诺应力则对应于流体微团的跳动引起界面两侧的动量交换，流体微团的跳动是由于湍流中大大小小的漩涡(即湍流脉动)引起的。雷诺应力并不是严格意义上的表面应力，它是速度脉动引起的动量交换在平均运动界面上的等效作用力。即对于平均运动而言，它具有表面力的效果，因而将其视为表面力。从这个意义上说，湍流平均运动的微元体除压力外还受到两种表面力作用，即分子黏应力和雷诺应力：

(8)

(9)

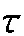
绝大部分流动中雷诺应力远大于黏应力，因此可将黏应力忽略；但在边界层内由于速度梯度很大，分子黏应力在离壁面一定距离内可以达到雷诺应力的量级，此时黏应力将不能被忽略。

层流边界层法向应力变化如图6所示。由图6可见，层流边界层内总应力与黏应力相近且变化趋势基本一致，说明黏应力占主导，壁面处二者均为0.45 Pa，而此处壁面剪切力为0.453 Pa，黏应力与壁面剪切力基本相同；雷诺应力占比极小且在黏应力衰减最快的区间出现了一个较小的峰值；在离壁面一定距离内黏应力保持不变，近似为一常数，存在一平缓阶段，之后快速衰减。

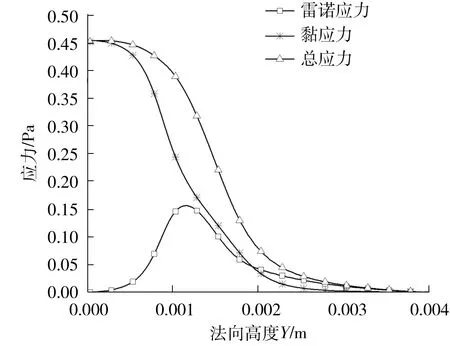
图6 层流边界层内的应力变化

湍流边界层法向应力的变化如图7所示，流体微团所受应力变化可以反映流动状态的变化。图8所示为湍流边界层内流向不同位置处的速度与离壁面距离两个参数无量纲化后的关系，通常物理量无量纲化后更能反映其中蕴含的物理规律。无量纲速度u+表达式如下：

(10)

图8中虚线所示的u+与y+的理论拟合曲线仿真结果基本吻合，说明了仿真结果的准确性。图8显示，当y+<5时，u+与y+基本满足虚线表示的拟合关系(u+=y+)；图7显示该范围内黏应力占主导而雷诺应力很小，说明该区域流动基本为层流，由于壁面的存在抑制了湍流脉动，故壁面处雷诺应力为零，壁面处黏应力达到最大值且等于总应力，约等于此处的壁面剪切力(1.39 Pa)。当y+>50时，u+与y+满足虚线所示的对数拟合关系(u+=2.5lny++5.21)，图7显示在此区域内黏应力基本降为零而雷诺应力占主导且与总应力基本相等，之后二者开始同步衰减，说明此过程中流动完全处于湍流状态且湍流脉动强度不断减低，该区域称之为对数区域；而在层流区域与对数区域之间边界层处于过渡状态，图7显示该区域内黏应力不断下降而雷诺应力不断上升，由层流底层中黏应力主导变为了对数区域中雷诺应力主导，说明流动由底层的层流状态过渡到对数区域的湍流状态，该区域为过渡区域；层流底层、过渡层以及对数律层构成了边界层内层；当y+>1 000时，两个位置处的u+与y+曲线均开始逐渐偏离对数规律而快速增长，图7显示在该区域边界层内所受雷诺应力与总应力均随y+值的增大同步衰减，当二者衰减接近零时，流动便由湍流变为了层流状态，此时离壁面的高度即为边界层的厚度，称此区域为边界层外层；图8显示流向不同位置(X=4,7 m)的u+与y+曲线在内层完全重合，而在偏离对数规律的外层二者出现分叉，这说明湍流边界层内不同位置上在内层以相同的规律增长，差异主要发生在外层。

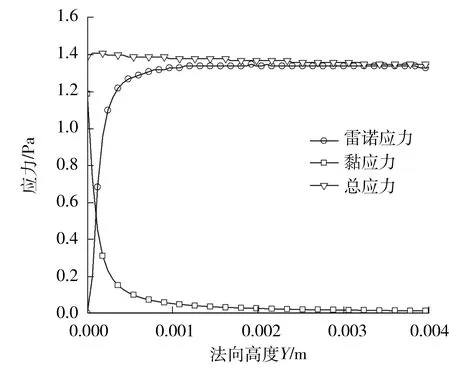
图7 湍流边界层法向应力变化

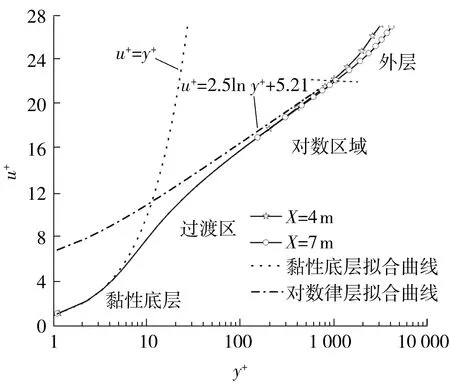
图8 湍流边界层内u+与y+的关系

转捩过程中雷诺应力与黏应力的变化如图9所示。

由图9可见，在沿流向的不同位置上，雷诺应力在法向上均由零增大到最大值，然后又衰减为零，转捩过程雷诺应力的最大值不断增大，而其达到最大值时对应的离壁面的距离却在不断减小，说明转捩首先发生于离壁面一定高度的区域，之后随着转捩的进行湍流区域不断向壁面延伸；对于黏应力，转捩过程中其在壁面处所达到的最大值不断增大，但其衰减速率变化更快，说明转捩过程中壁面附近层流区域不断减薄。结合上述应力分析可以得出，壁面剪切力无论层流还是湍流均由黏应力产生，转捩前后剪切力突变是由于转捩过程中壁面处黏应力发生了突变。

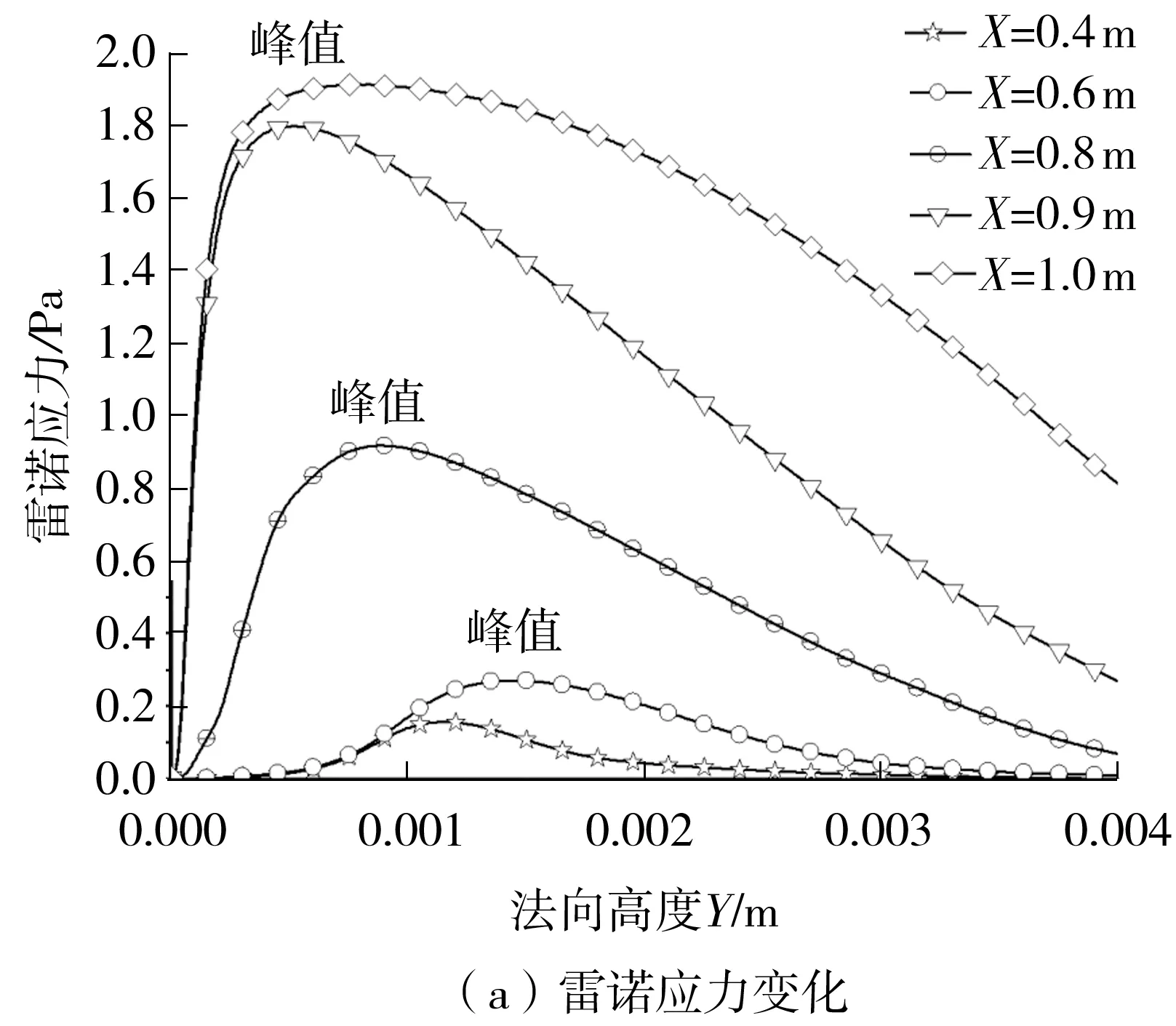
图9 转捩过程中的应力变化

3 影响边界层发展的因素

3.1 平板粗糙度、湍流度、风速的影响

前文为平板粗糙度为0、湍流度为1%、风速为30 m/s时地板边界层的研究结果，本节计算模型与前文一致，只改变单个变量来研究平板粗糙度、湍流度、风速对边界层发展变化的影响。

实际任何平板表面总有不同程度的粗糙度，不同的粗糙表面有不同的几何形状、高度以及分布密度，每个因素的不同都会形成不同的粗糙表面，都会对边界层内的速度分布产生影响。此处假设粗糙元的几何形状与尺寸等其他参数一致，只考虑粗糙元高度不同带来的影响。此处给出壁面粗糙元雷诺数的定义：

(11)

式中,h与h+分别为粗糙元实际高度与无量纲高度，计算中给出的参数如表1所示。

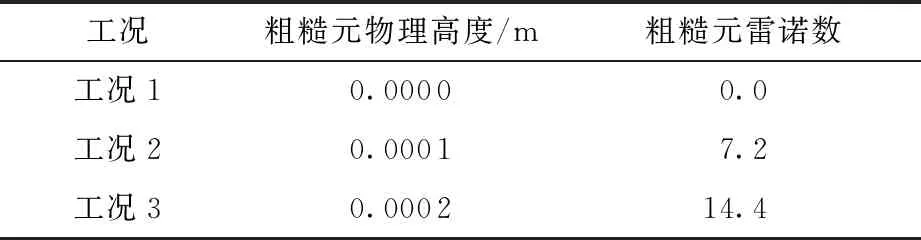
表1 计算工况

不同壁面粗糙度下剪切力的变化如图10所示。

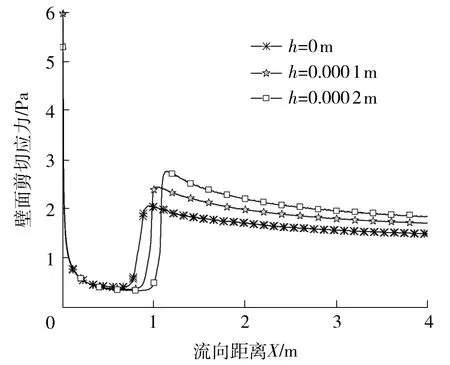
图10 不同壁面粗糙度下剪切应力的变化

由图10可见，随着粗糙度的增大，转捩区间整体后移，转捩后形成的剪切力增大。图11显示，不同壁面粗糙度的y+与u+曲线在y+约为10的位置相交，随着粗糙度增大，y+小于10时的曲线逐渐偏离线性关系而接近对数关系，说明层流底层逐渐消失融入了对数律层，且对数律层所满足的对数关系并未发生改变，其他分层整体下移。结合图12可知，粗糙度越大转捩后形成的湍流边界层厚度的增长率越大。

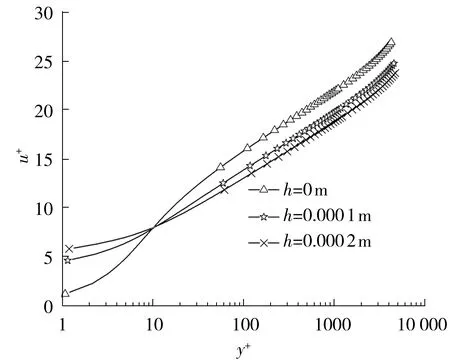
图11 不同壁面粗糙度下湍流边界层内u+与y+的关系

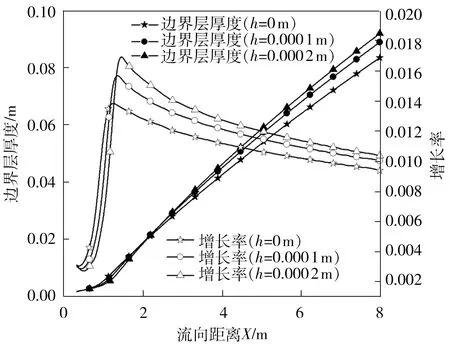
图12 不同壁面粗糙度下边界层厚度及其增长率的变化

湍流度Tu反映了湍流中脉动速度(u′，v′,w′)相对平均速度u∞的大小，其定义如下：

(12)

不同湍流度下壁面剪切应力的变化如图13所示。

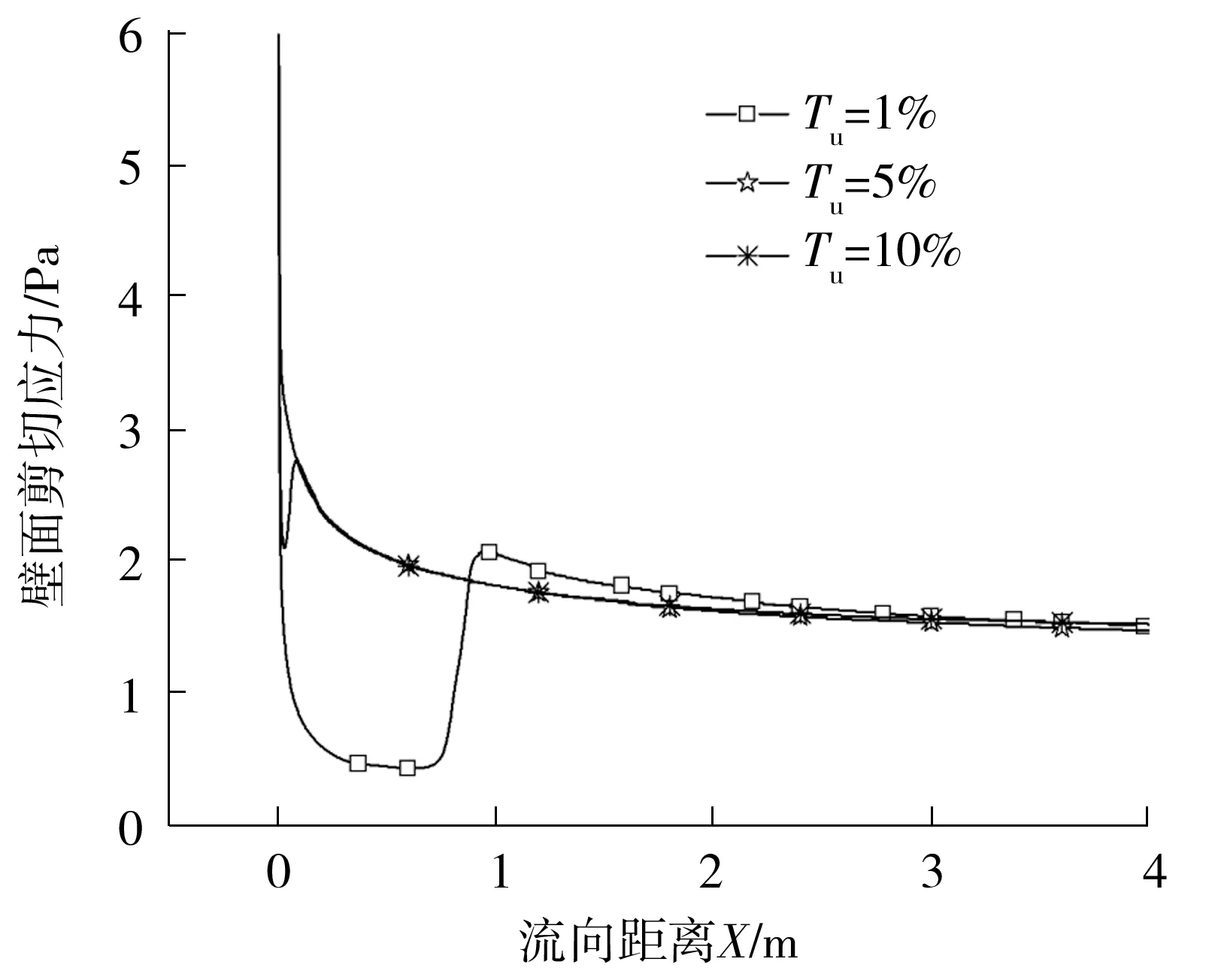
图13 不同湍流度下壁面剪切应力的变化

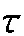
不同湍流度下壁面边界层的厚度及其增长率的变化如图14所示。

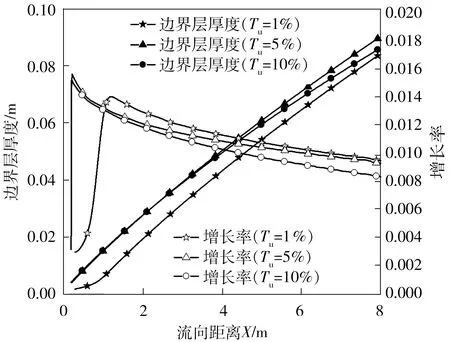
图14 不同湍流度下壁面边界层厚度及其增长率的变化

由图14可见，随着湍流度的提高，湍流边界层厚度的增长率反而会下降；与湍流度为1%时不同，在湍流度为5%与10%时，边界层厚度增长曲线及其增长率曲线均没有明显的因边界层转捩而产生的突变。在图15中，在不同湍流度下边界层内u+与y+曲线重合，说明湍流度的改变虽然会对边界层厚度及其增长率产生影响，但是不会影响边界层内结构分层以及法向增长规律。

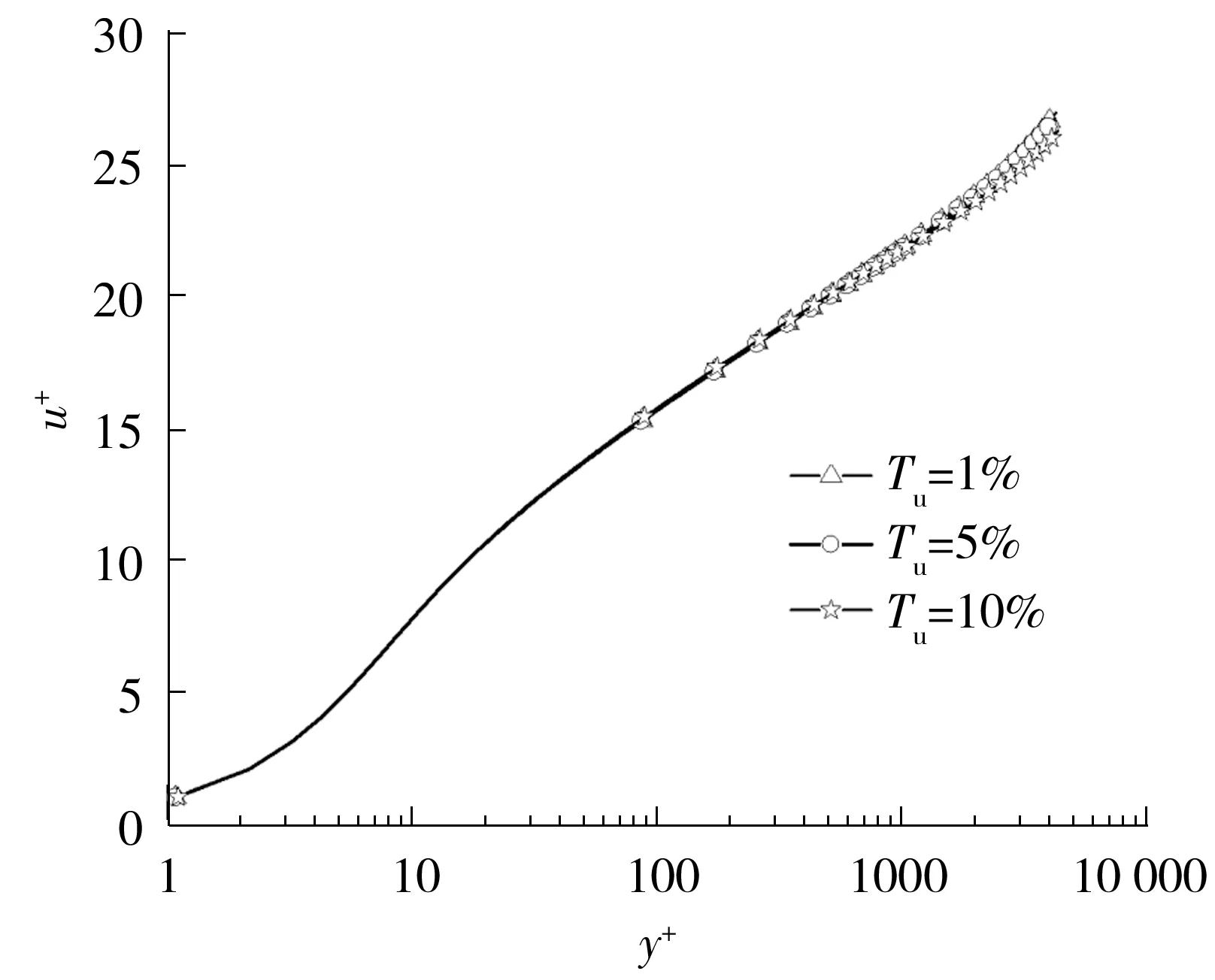
图15 不同湍流度下湍流边界层内u+与y+的关系

不同风速(U)下壁面剪切应力的变化如图16所示。由图16可见，风速的提高使转捩起点与终点均大幅前移且转捩区间缩短，无论层流还是湍流边界层，壁面剪切力均随风速的提高而增大。

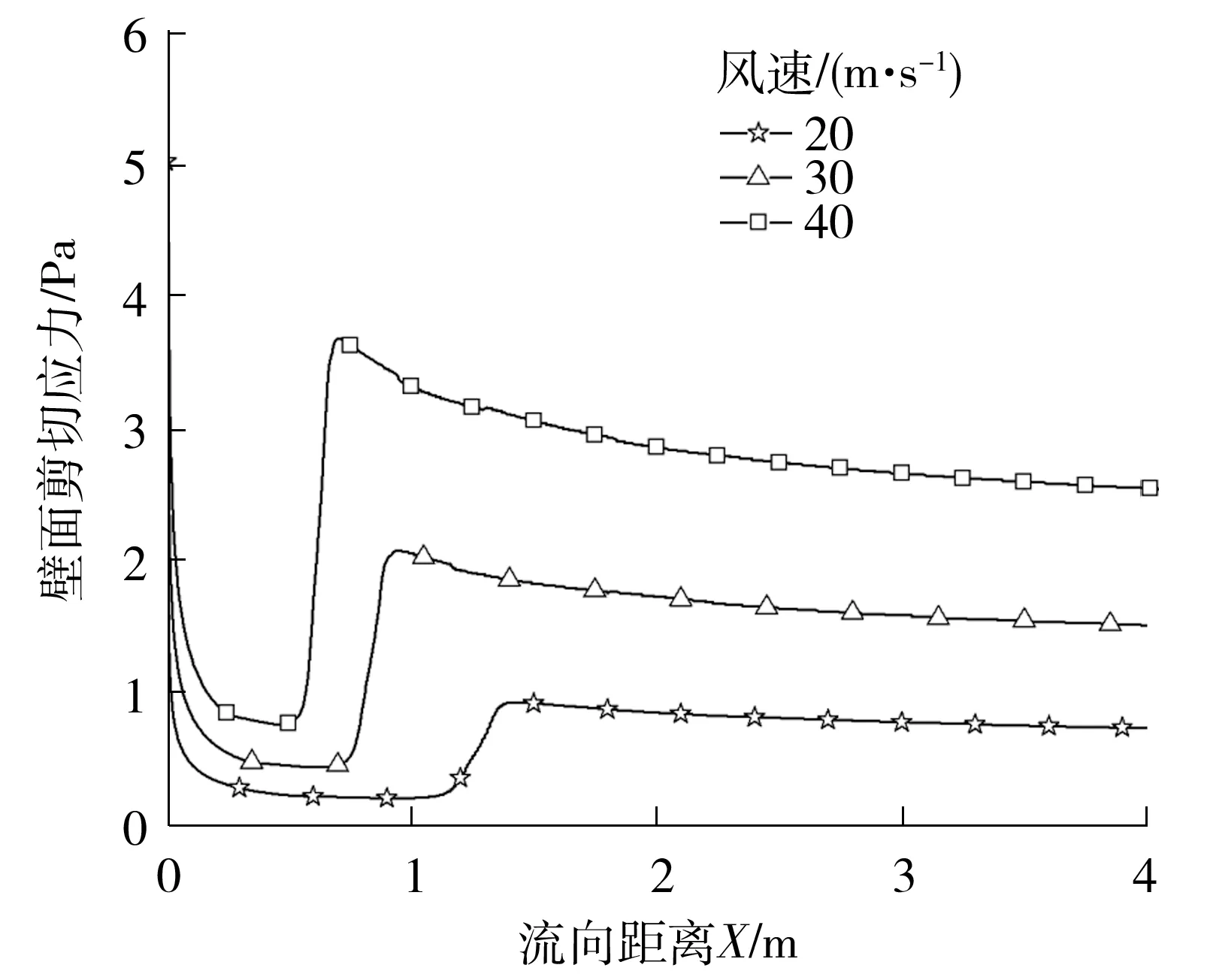
图16 不同风速下壁面剪切应力的变化

不同风速下边界层厚度及其增长率的变化如图17所示。

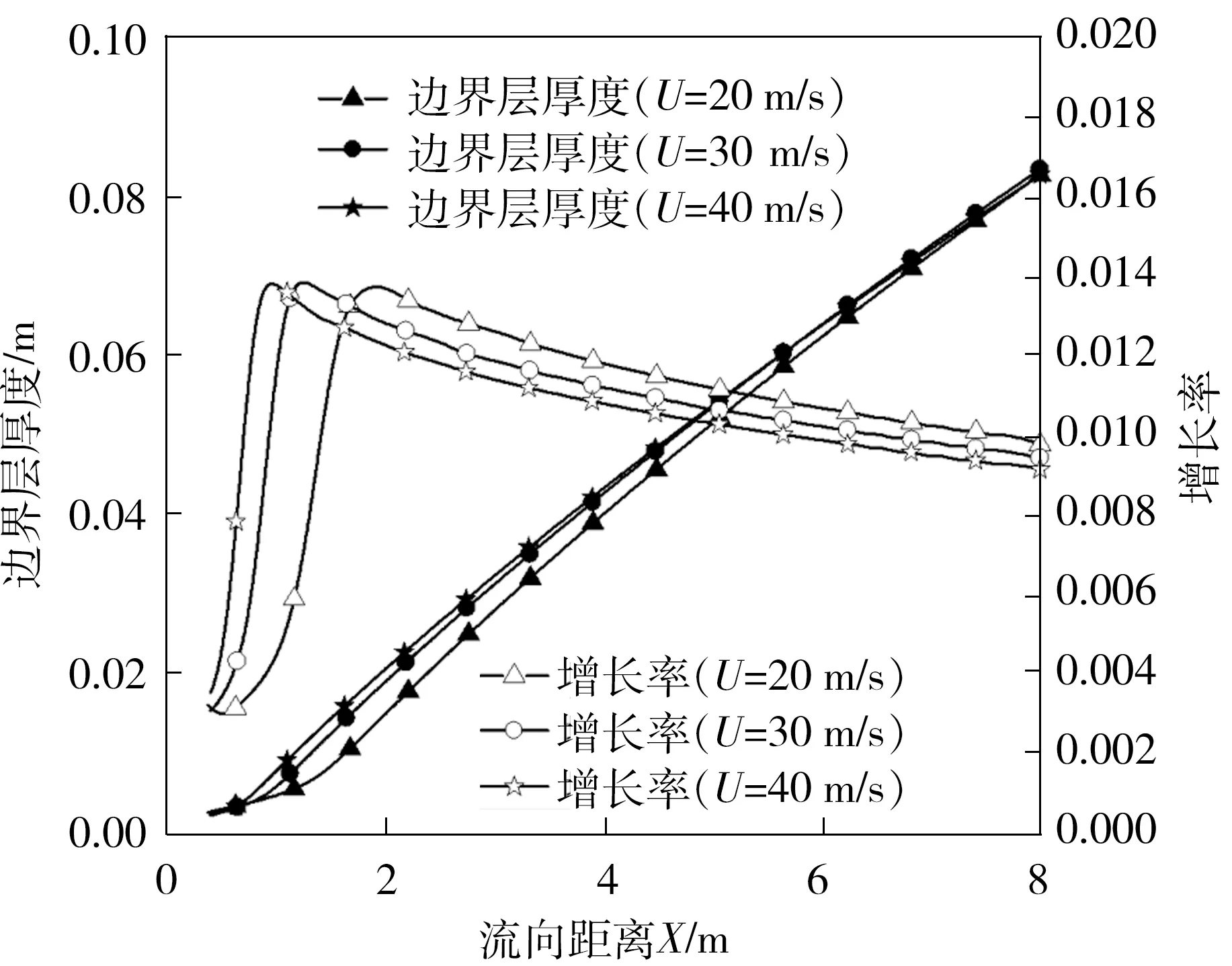
图17 不同风速下边界层厚度及其增长率的变化

由图17可见，风速越高，转捩后形成的湍流边界层的增长率越低。

不同风速下u+与y+值的变化如图18所示。

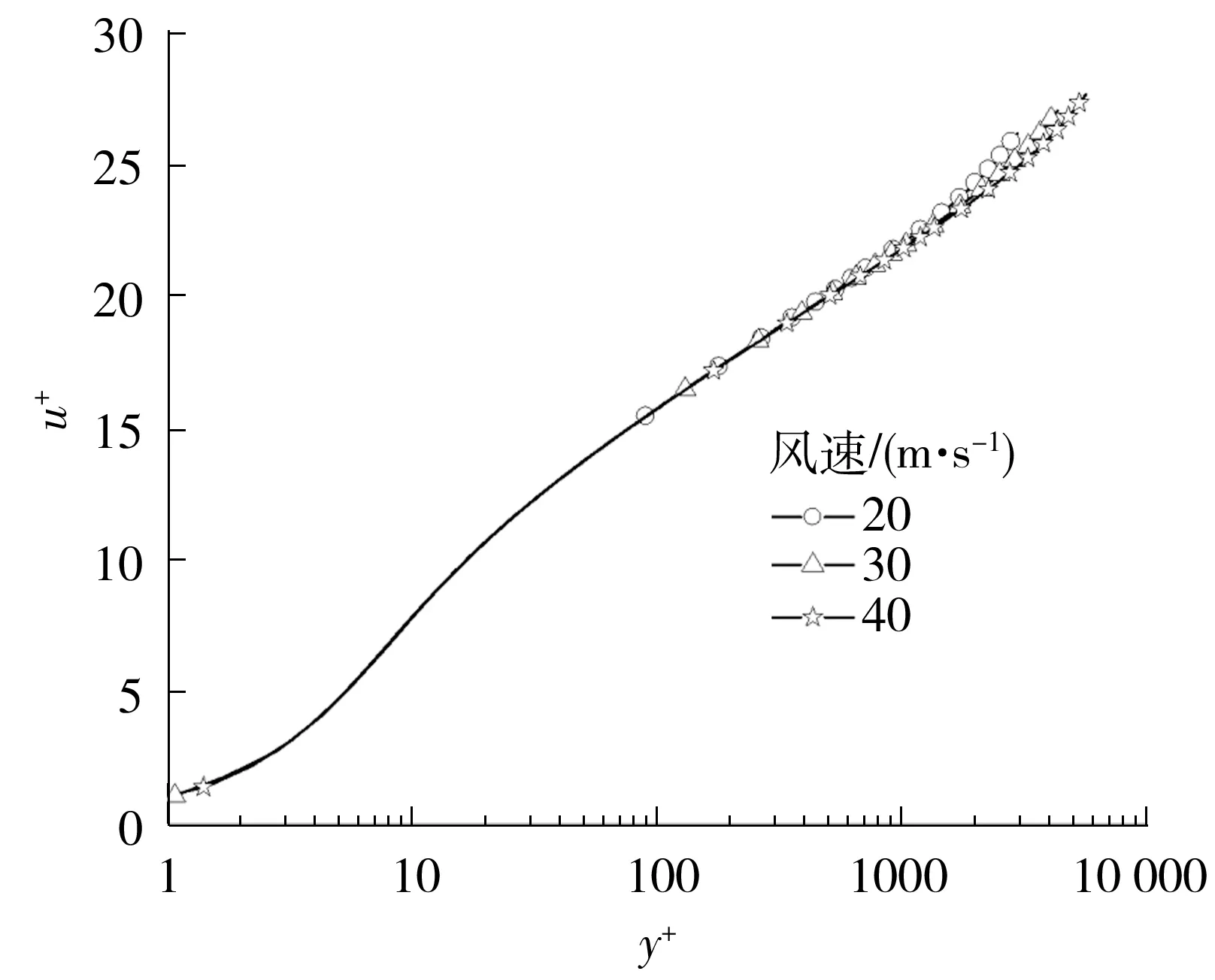
图18 不同风速下湍流边界层内u+与y+的关系

由图18可见，不同风速下边界层的u+与y+曲线在边界层的内层重合，在边界层外层开始出现分叉。表明不同风速(即不同来流雷诺数)对边界层转捩以及边界层增长率有明显的影响，对边界层内层没有影响，但对边界层外层会产生明显的影响，不同风速会改变边界层外层的增长规律。

3.2 压力梯度的影响

与平板边界层不同，实际上具有复杂形面的物体表面边界层变化更加复杂，这主要是流场中产生的局部压力梯度与风速的变化导致的。压力梯度的变化会对边界层的发展变化产生很大影响，计算域顶部按一定曲率变化可以在保证计算域底部流场稳定的同时在计算域内形成一恒定的压力梯度。为在下壁面形成一个50 Pa/m的压力梯度，根据总压公式有

p1(x)+0.5ρv(x)2=p2(x)

(13)

式中:p1表示静压;p2表示总压,为一常数。两边同时取微分后可得

(14)

等式两边同时积分求解该偏微分方程并保证流量与上述模型一致可以求得计算域上壁面高度为

(15)

根据上述表达式建立的顺压梯度计算域如图19所示(逆压梯度同理)。

图19 顺压梯度计算域示意图

不同压力梯度下壁面剪切应力的变化如图20所示。

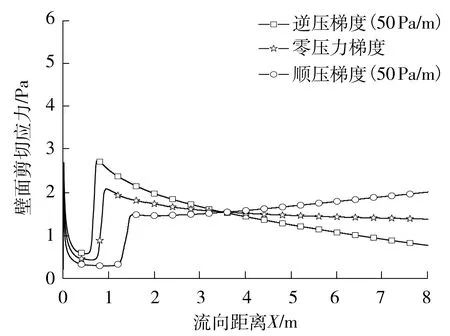
图20 不同压力梯度下壁面剪切应力的变化

由图20可见，随着压力梯度由顺压梯度变为逆压梯度，转捩起点与终点不断前移，转捩区间不断缩小；逆压梯度下最先发生转捩且转捩后壁面剪切应力最高，之后则不断降低；顺压梯度下最后发生转捩且转捩后的壁面剪切应力最低，之后则不断升高；零压力梯度下则介于二者中间。

不同压力梯度下边界层的厚度及其增长率随流向距离X的变化如图21所示。

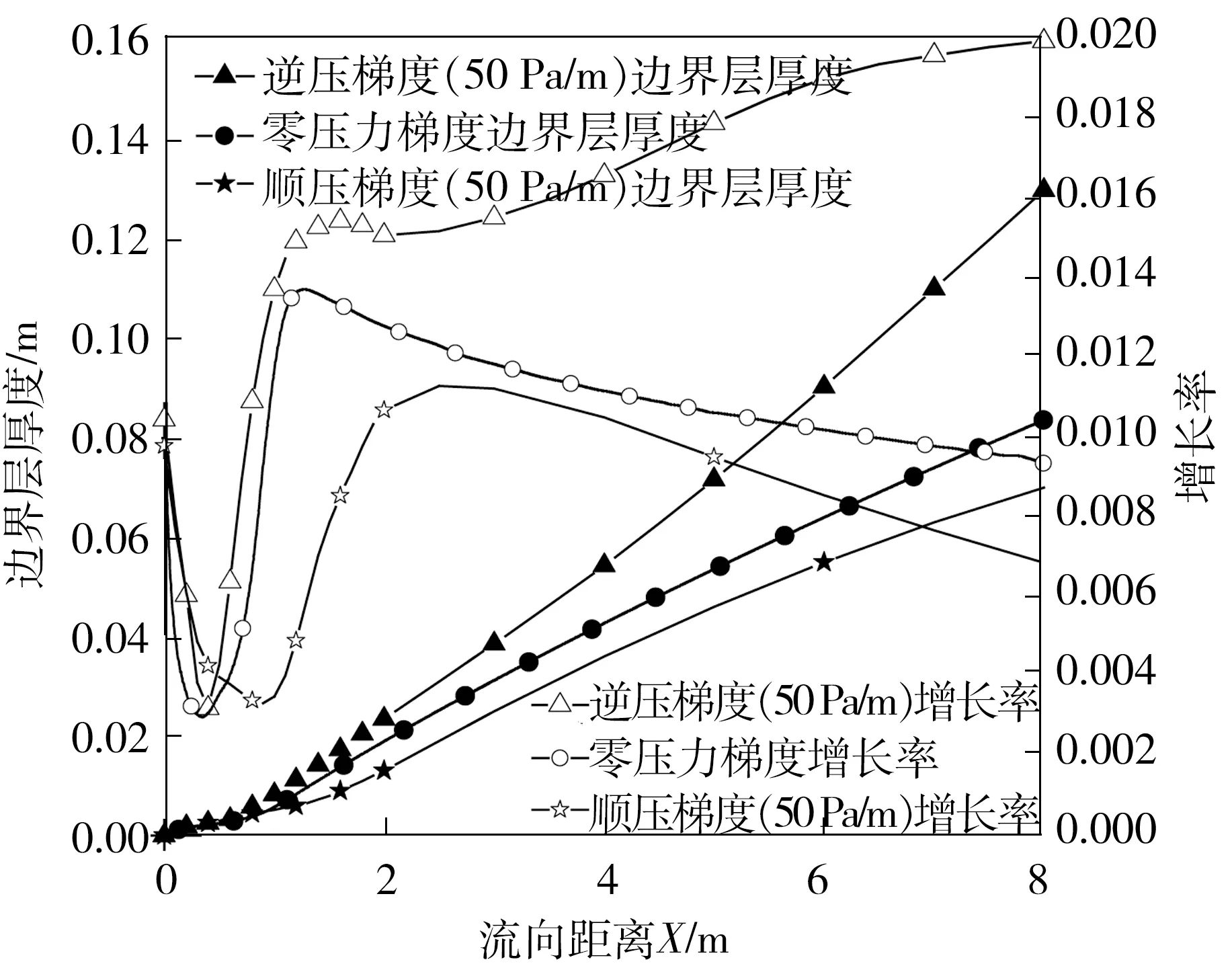
图21 不同压力梯度下边界层厚度及其增长率的变化

由图21可见，逆压梯度时边界层厚度及其增长率最大，顺压梯度时边界层厚度及其增长率最小，零压力梯度则居于二者之间；顺压梯度不仅推迟了边界层转捩，且有助于抑制边界层的发展增厚。

取X=4 m做不同压力梯度下边界层的u+与y+关系曲线，如图22所示。

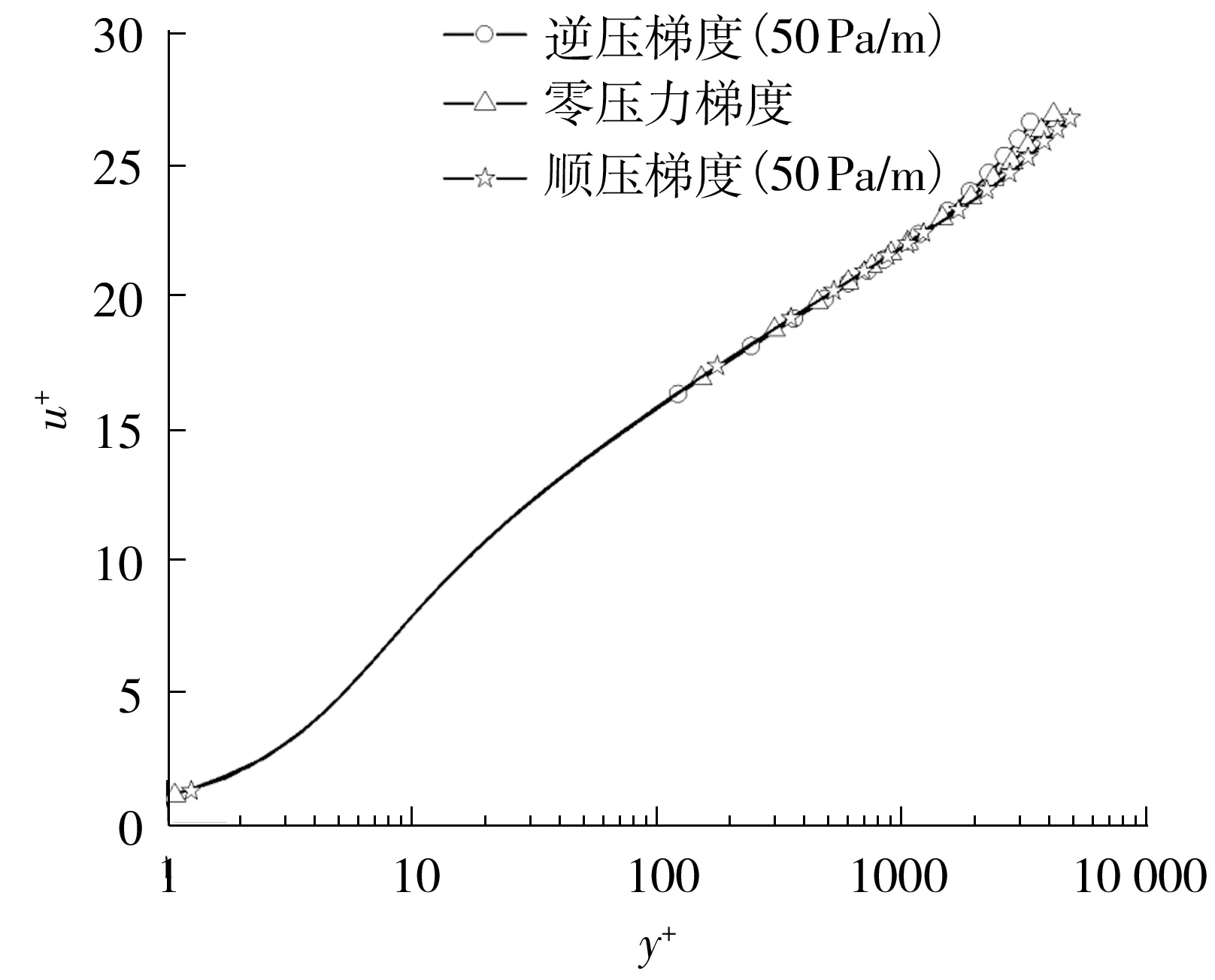
图22 不同压力梯度下湍流边界层内u+与y+的关系

由图22可见，虽然不同压力梯度下湍流边界层厚度及其增长率相差很大，但是法向上在层流底层、过渡层、对数层以及湍流边界层外层，其u+与y+曲线重合，这说明压力梯度会改变边界层的厚度及其增长率，但是不会对边界层内的结构分层产生影响。

4 结论

本文采用γ-Reθt转捩模型对平板表面边界层进行了数值模拟，研究了边界层在法向和流向上的变化以及壁面粗糙度、来流风速、湍流度、压力梯度等因素对边界层发展的影响。得到以下主要结论：

(1)在转捩区间(距平板前缘0.75～1 m的范围内)，壁面摩擦系数发生了突变，边界层厚度沿流向不断增厚但其增长率不断下降；转捩过程中，速度型发生了明显的变化，层流与湍流边界层法向速度梯度相等处可监测到流向总压在转捩区间最大的突变。

(2)层流边界层内的应力以黏应力为主，其在一定高度内保持稳定之后迅速衰减，在其衰减最快的区间雷诺应力产生一较小的峰值；湍流边界层法向上应力变化依次经历黏应力占主导、黏应力迅速衰减而雷诺应力迅速增大、雷诺应力占主导3个阶段，分别对应湍流边界层内的层流底层、过渡层、对数层与外层；转捩过程中，雷诺应力的峰值不断增大且达到峰值时对应的法向高度不断降低，黏应力在壁面处达到的峰值不断增大但其法向上的衰减变得更快。

(3)壁面粗糙度的增大推迟了转捩区间，提高了湍流边界层的增长率，使湍流边界层的黏性底层消失，其他分层整体下移；湍流度的增大与风速的提高使转捩提前的同时缩短了转捩区间，降低了湍流边界层的增长率，二者不会影响湍流边界层内的结构分层；压力梯度的增大会推迟边界层的转捩，同时扩大转捩区间，大幅降低边界层增长率但是不会影响边界层的结构分层。