填充速度对制件拐角轮廓部位熔融沉积精度与打印效率的影响

陈松茂 陈宇林

(华南理工大学 机械与汽车工程学院,广东 广州 510640)

熔融沉积3D打印技术(Fused Deposition Mo-delling,FDM)具有简单便捷、成本低廉和环境友好等优点[1- 2]，被广泛应用于制造领域[3- 7]。然而受材料性能、台阶效应等多因素制约，制件质量并不十分理想，尤其是非直线外轮廓区域[8- 9]。

三维模型切片后，每一层外轮廓可大致分为直线轮廓、拐角轮廓和曲线轮廓3种类型。理论上，熔融沉积直线轮廓时，没有材料重复沉积或漏沉积现象，成形精度和表面质量较好；而拐角或曲线轮廓则存在重复沉积区或漏沉积区缺陷且精度偏差较大。以拐角轮廓为例，可分为凸角和凹角两种，如图1所示。图1中圆形虚线表示喷嘴孔投影，虚直线表示喷嘴扫描轨迹，粗实线表示模型当前层切片外轮廓，α表示拐角角度大小。

由图1可见，凸角和凹角处均不可避免地存在重复沉积区和漏沉积区两种结构缺陷。其中：①填充凸角轮廓时，漏沉积区会直接增加轮廓精度误差和表面粗糙度值；重复沉积区中材料重复堆积并挤压轮廓线向外扩张，也会增加该误差。②凹角轮廓漏沉积区所缺材料可以在填充制件内部区域时给予弥补，但重复沉积区中材料重复堆积并挤压轮廓线会引起轮廓精度误差。③拐角角度越小，重复沉积区和漏沉积区面积越大，对轮廓的成形精度和表面质量影响越大，凸角中更为明显。④凸角或凹角的重复沉积区或漏沉积区面积理论上是几何对称、大小相等的，其函数关系与曲线分别如式(1)、图2所示(图中示例采用孔径为φ0.4 mm的喷嘴)。

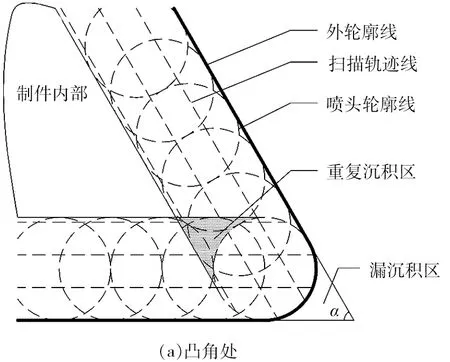
图1 不同拐角处的重复沉积区和漏沉积区

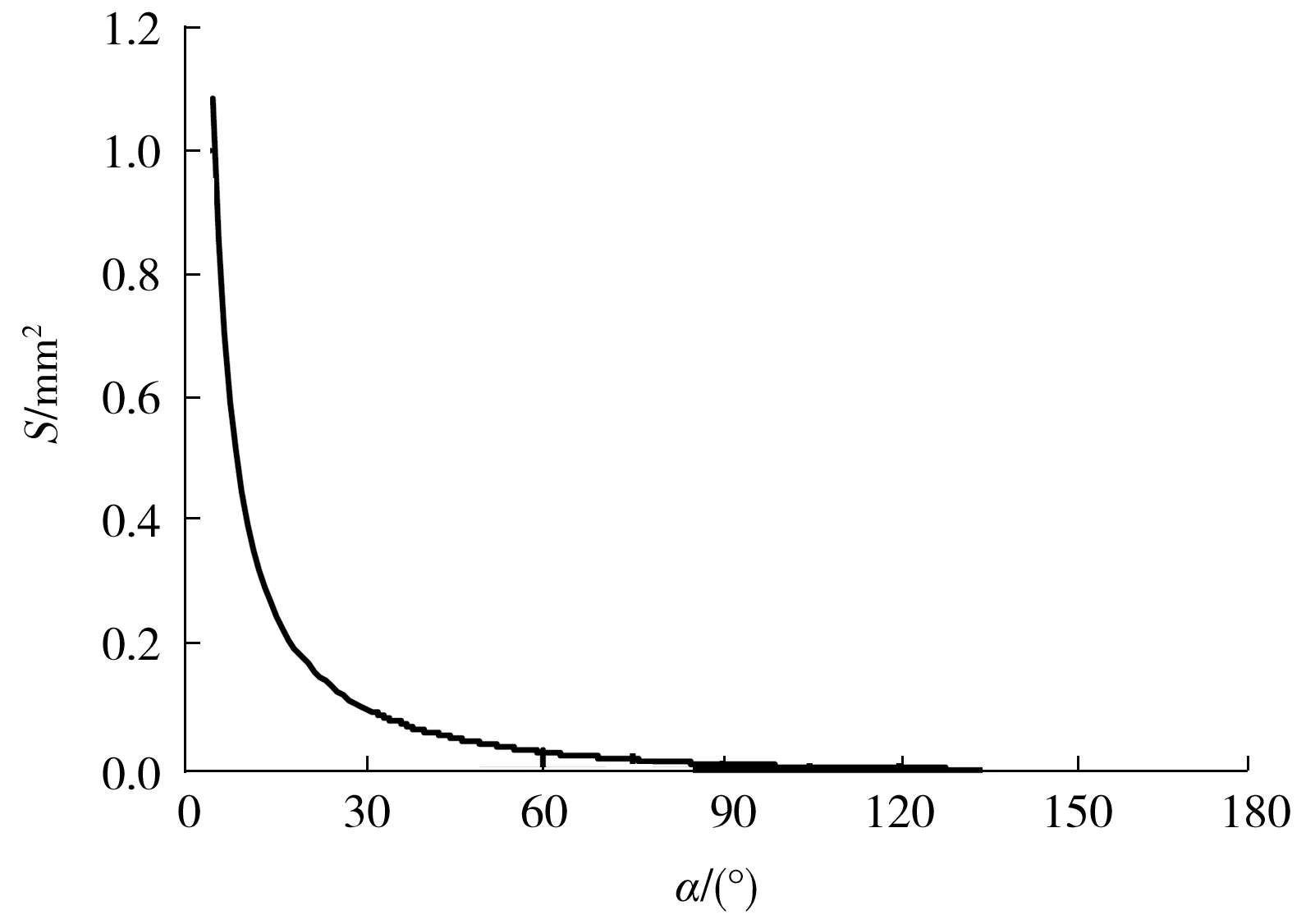
图2 重复沉积区或漏沉积区面积的理论函数曲线

(1)

式中：S为重复沉积区或漏沉积区的理论面积；拐角角度α在(0，180°]区间变化；R为喷嘴孔轮廓半径。

由式(1)和图2可知，当R恒定时，S随着α增大而减小；α越接近0°，S越大，拐角越尖锐，引起的精度偏差也越大；α超过90°后，S变得越来越小，偏差也就越小；当α接近180°时，拐角轮廓扫描轨迹近乎为一条直线，S趋于0。

许多学者针对拐角轮廓的沉积问题展开了研究。Armillotta等[10]通过分析由台阶效应、支撑效应、半径效应、偏移和边界弯曲效应、切片和熔模膨胀等综合作用产生的几何误差，提出了一种模拟制件边缘轮廓的方法，推导出了拐角轮廓边缘位置与层厚、拐角大小之间的关联函数公式，可预测名义边缘形状偏差。Brooks等[9]分析了不同直径的喷嘴在填充拐角轮廓时产生的成形精度误差对分层厚度、打印效率的影响，同时设计了一个具备内外层两级直径的喷嘴结构，很好地兼顾了60°以内凸角轮廓的成形精度和打印效率。Wu等[11]采用机器视觉和轮廓控制技术，通过提取FDM制件每一层横截面轮廓数据并进行轮廓误差计算，有效检测出拐角轮廓实际形状。Taufik等[12]分析了外轮廓、内轮廓、外轮廓+内轮廓3类边缘轮廓，认为轮廓偏差因子取决于工艺参数且对表面粗糙度有重大影响，同时根据边缘轮廓实际偏差构建了一个描述轮廓曲线精度的数学模型，可有效预测制件表面的粗糙度值。此外，值得一提的是，在非FDM过程中也有相关研究。Friedrich等[13]采用墨水直写技术(Direct Ink Writing，DIW)打印制件时发现，拐角轮廓的重复沉积和漏沉积缺陷是引起成形精度误差的重要因素之一。Woo等[14]在直接能量沉积过程(Directed Energy Deposition，DED)中应用拐角扫描速度控制算法和相关经验公式补偿扫描速度在拐角处的下降，控制矩形拐角处的过度沉积现象，使拐角处沉积高度与其他直线段等高且光滑，并使用多元回归分析了DED工艺参数和成形珠粒尺寸间的相关性。类似的，在微金属液滴沉积制造过程(Micro Metal Droplet Deposition)中，Zhang等[15]针对拐角处的多余沉积问题进行了研究，提出了相关数学模型并根据拐角大小和液滴总数补偿液滴间的中心距以优化该距离，该模型可使液滴沉积的位置一直落于扫描线上，并且在拐角处的相邻液滴中心距处于最佳范围内，尽管液滴的成形过程是离散的，但由于离散分辨率足够高，该补偿方法仍可以拓展至聚合物或金属等材料的相对连续的固化过程中，不限于微金属液滴。

相关研究表明[16- 17]，在熔融沉积过程中，受填充速度和熔丝挤出速度等因素影响，拐角处重复沉积区或漏沉积区的实际面积与理论面积S差异较大。因为在扫描拐角轮廓时，由于扫描路径的突变性与熔丝挤出的滞后性，填充和挤出速度瞬时不同步，引起拐角处熔丝沉积量误差，导致重复沉积区或漏沉积区的实际面积增加[18]，降低了拐角成形精度。上述文献研究了FDM及其他成形原理中拐角处的质量问题，还需深入详细讨论填充速度与拐角轮廓成形精度、打印效率之间的影响机制及优化控制方法。因此，本研究结合实验与数学分析方法，研究了拐角轮廓熔融沉积成形过程中填充速度与成形精度、打印效率之间的作用规律，并提出了拐角轮廓填充速度自适应控制的初步思路。由于α>90°时拐角处的重复沉积或漏沉积缺陷对拐角精度影响较小，故本研究重点对0<α≤ 90°的凸角轮廓进行论述。

1 实验方法

1.1 试样设计

设计了如图3示的6种拐角大小不同的四边形试样，依次记为试样Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ，对应的α取值分别为15°、30°、45°、60°、75°、90°。所有试样最长边长为60 mm，宽为15 mm，厚度为6 mm。

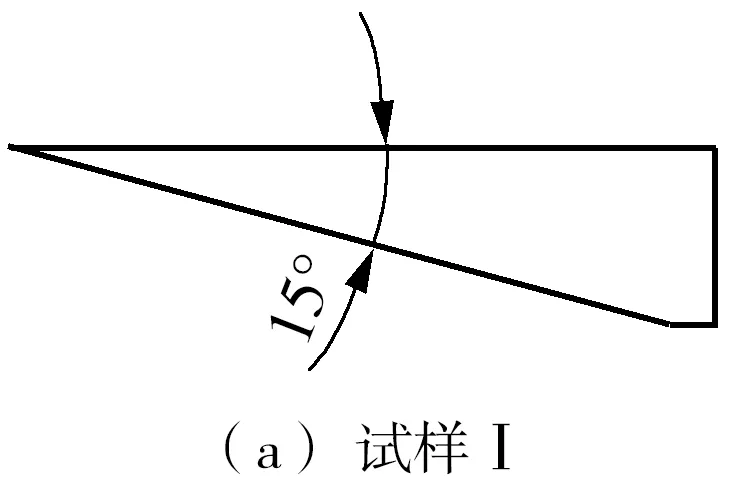
图3 具有不同拐角的试样

1.2 评价指标

选取拐角的重复沉积区实际面积S1与漏沉积区实际面积S2之和S0作为成形精度评价指标，S0越大则精度越差；选取打印耗时t作为打印效率评价指标，t越大则效率越低。

1.3 实验材料

采用国产某型号聚乳酸(PLA)丝材，直径为φ(1.75±0.02)mm，密度为(1.25±0.05)g/cm3，熔化温度范围为190～220 ℃。该PLA树脂质量分数大于60%，符合GB/T 29284的规定，由FDM成形的PLA试样拉伸强度可达60 MPa，断裂伸长率大于3%，弯曲强度大于60 MPa。

1.4 实验装置

高诺A001型国产桌面型FDM设备，喷嘴孔径为φ0.4 mm；德国BRESSER专业级全金属数码显微镜MDA2000，最高分辨率20万像素，最高倍率200倍。

1.5 实验方案

1.5.1 工艺参数设定

打印试样时，变量为拐角α和填充速度v，α、v和其他定参数的取值如表1所示。

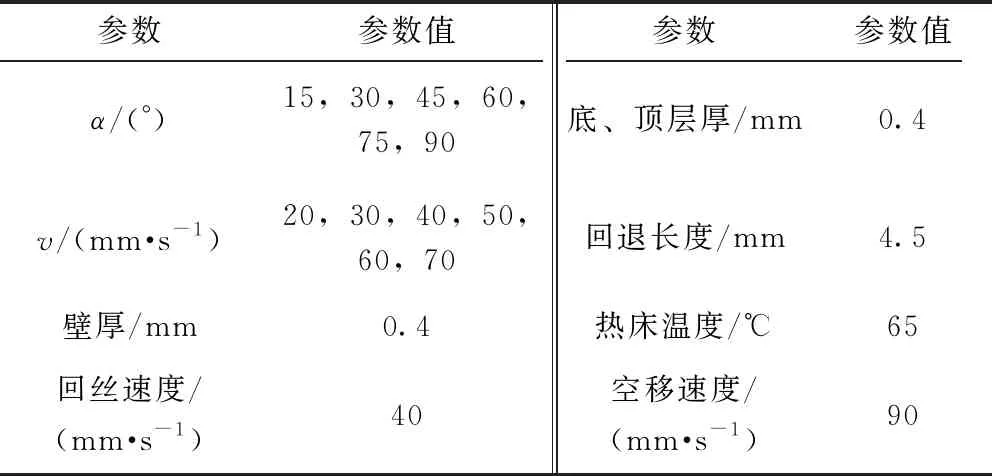
表1 各工艺参数取值

1.5.2 评价指标测量方法

在MDA2000工作台上拍摄已打印试样的实际轮廓，设置放大倍率为40倍，固定玻璃标尺。利用计算机软件描边标定重复沉积区和实际漏沉积区的轮廓。以试样Ⅰ(α=15°)为例，实际重复沉积区与漏沉积区面积标定结果如图4所示。图中的方格型阴影部分为已标定的实际重复沉积区S1，斜线型阴影部分为实际漏沉积区S2。借助CAD软件近似测量和计算S1、S2，获得S0。实验重复3次，记录每次对应的S0、t，取平均值。

图4 实际重复沉积区与漏沉积区面积标定示例(α=15°)

2 结果分析与讨论

2.1 填充速度对拐角轮廓成形精度的影响

填充速度v=20 mm/s时各试样拐角成形效果如图5所示。由局部放大图可知，拐角处实际轮廓线与理论轮廓线存在不同程度的偏差。其中试样Ⅰ凸角钝化较为严重，S1和S2相对较大，轮廓偏差比较明显；随着α的增大，对应的试样Ⅱ-Ⅵ钝化现象逐渐减弱，拐角精度逐步增加。

图5 不同试样的拐角成形效果(v=20 mm/s)

不同填充速度v下成形精度指标S0与拐角角度α之间的关系如图6所示。由图6可见:S0关于α的曲线同样呈现出近似递减趋势，且α越大，拐角成形质量越高，这与之前的理论分析一致；结合图2中各个α值对应的S值可知，不同v下的S0均大于理论值S，且其差值(S0-S)随着v增大而增大，因为填充速度与挤出速度自动同步匹配[15]，本实验所用机型也遵循此设定，填充速度和挤出速度同增同减；同时，FDM材料在熔融-沉积-固化过程仍具备一定的流动性，由于拐角轮廓处的路径突变，再加上喷嘴孔的形状自身就是一个圆孔，无法完全拟合拐角形状，从而带来之前所述的两类误差，并且在速度增加时，熔丝挤出受到更大的牵引力，自由收缩量更大，尤其是拐角处，这种收缩将增大拐角误差，上面各种原因综合，导致高速成形拐角时拐角质量容易变得较差。

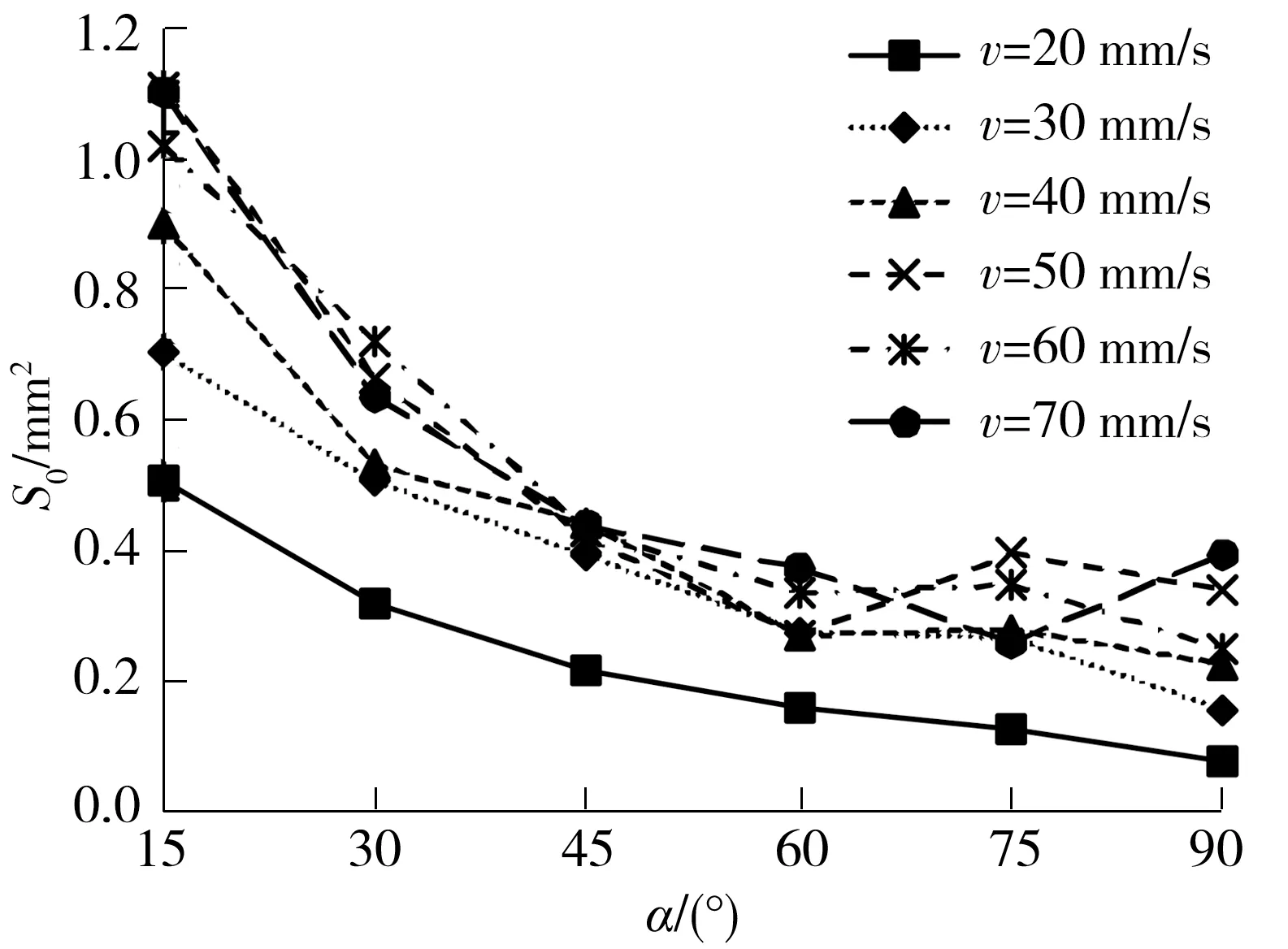
图6 不同填充速度下S0与α的关系

不同拐角下成形精度指标S0与填充速度v之间的关系如图7所示。由图7可见:各曲线变化趋势并不完全一致。相对低速范围内(v≤50 mm/s)，S0总体上随v的增大呈递增趋势，因此选择较小填充速度打印拐角轮廓可提高成形精度。当v>50 mm/s时，S0呈现出了不同的变化规律;α=15°,45°,90°时，S0并未随v的增大而增大，而是先下降后上升(下降幅度为0.02～0.14 mm2);α=75°时，S0随v的增大而一直下降(幅度超过0.15 mm2)，α=30°和60°时，S0总体呈现递增趋势(上升幅度分别为0.12 mm2和0.16 mm2)。总体上高速区间的S0比低速区间的大，在成形精度要求高时不宜采用过高的填充速度，但也存在高精度高效率打印的可能(如α=75°时以70 mm/s打印及α=90°时以60 mm/s打印)。

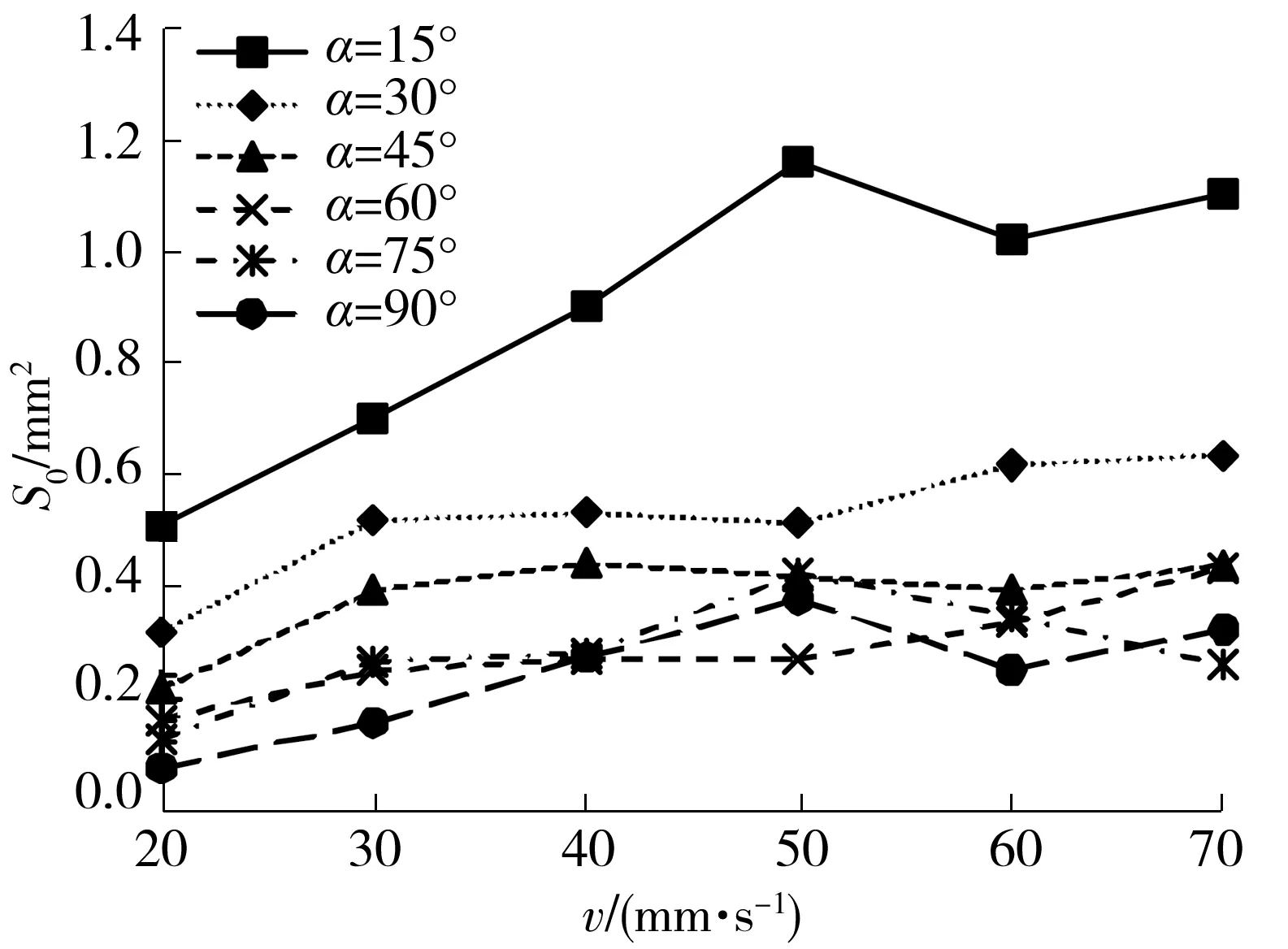
图7 不同拐角下S0与v的关系

2.2 填充速度对拐角轮廓打印效率的影响

FDM精度与效率是相互矛盾的，填充速度快时，打印效率较高，但成形精度得不到保障；填充速度慢时，精度较高，但打印效率较低。FDM设备喷头在填充过程中主要作匀速运动，在路径变化时作相应加减速运动。受设备加速度极限限制，打印效率不能无限提升，当填充速度提高到某水平且打印耗时基本不能再下降时，即为最低耗时(或最高效率)。本研究中试样Ⅰ-Ⅵ的拐角及形状不同，路径规划存在差异，对应的最低耗时也不同。各试样打印耗时t与填充速度v之间的关系如图8所示。

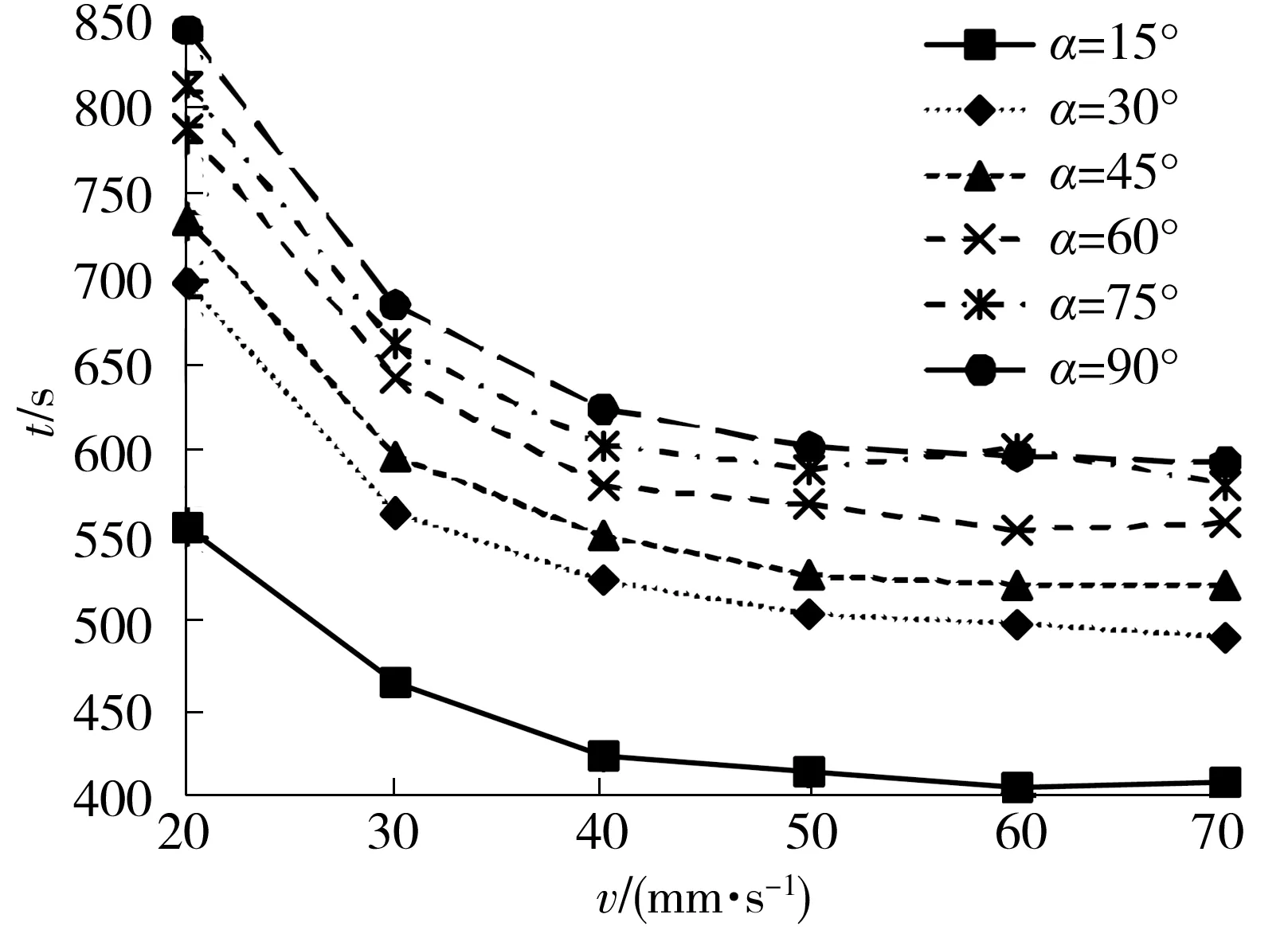
图8 不同试样的t与v的关系

由图8可见，6种填充速度下，试样Ⅰ-Ⅵ的最低耗时约为400、500、525、550、575、600 s，比值约为1∶1.25∶1.31∶1.38∶1.44∶1.50，而各试样的体积比值为1∶1.47∶1.64∶1.74∶1.81∶1.87，最低耗时并不完全与试样体积成一一对应比例关系，随着体积的增加，相互耗时比反而下降，证明体积增加后匀速填充的路径占比更大了，而加减速等过程的路径占比更小了；当填充速度v超过50 mm/s后，各试样打印耗时逐步趋于某稳定值，说明填充速度对打印效率的影响逐步减弱。

2.3 拐角轮廓最优填充速度连续函数的构建

由以上分析可知，自适应地调节填充速度可在保证拐角轮廓成形精度的同时兼顾打印效率。因此，采取加权法，对成形精度和打印效率设定权重比例，可以推导构建最优填充速度连续函数，过程如下。

(1)假设某拐角轮廓、某一填充速度对应的轮廓成形精度指标S0为Smedium，该拐角下成形精度指标最大值和最小值分别为Smax、Smin，ps为成形精度的权重，可通过式(2)计算Smedium在该精度区间的位置，ps值越大则Smedium越大，精度越差，表明该填充速度越不合适选用，反之亦然。同理，假设某拐角轮廓、某一填充速度对应的打印耗时为tmedium，该拐角下最大耗时和最小耗时分别为tmax、tmin，pt为打印效率的权重，可通过式(3)计算tmedium在该打印效率区间的位置，pt值越大则tmedium越大，效率越低，表明该填充速度越不合适选用，反之亦然。

Smedium=Smin+ps(Smax-Smin)

(2)

tmedium=tmin+pt(tmax-tmin)

(3)

将实验结果代入式(2)、式(3)中进行计算，可得表2所示的各拐角与填充速度对应的ps和pt。

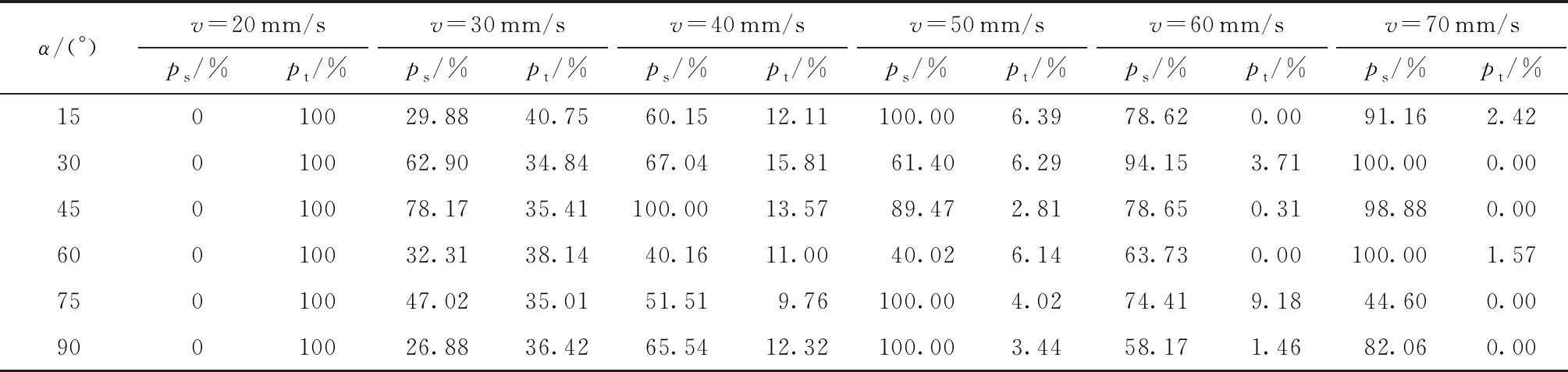
表2 不同拐角与填充速度对应的ps和pt

(2)S0和t的维度不同，可通过加权实现可加性与可比性。假设总百分比p为ps和pt的加权平均和，A和B分别为精度和效率对应的权重系数，且A+B=1，则有式(4)：

p=A·ps+B·pt

(4)

由定义可知，按照偏好分配好权重后，某拐角中使p值最小时对应的填充速度v能使效果最接近偏好，理论上而言其成形质量相对较佳，将这种情况下的v值命名为最优填充速度vop。经计算，当精度的权重系数A超过0.75时，试样Ⅰ-Ⅵ的vop的取值基本均为20 mm/s；当效率的权重系数B超过0.6时，试样Ⅰ-Ⅵ的vop取值依次固定为60、50、60、50、70、60 mm/s。因此，可认为，A为0.75～1时成形精度优先；A为0～0.4时打印效率优先；A为0.4～0.75时同时兼顾了精度与效率问题，在满足精度要求情况下，A应尽可能小。

(3)由经验假设A=B=0.5能使试样拐角具有较高成形精度的同时保证其打印效率，则可计算获得试样Ⅰ-Ⅵ的最优填充速度vop分别为30、50、60、50、70、60 mm/s。将以上数据导入Matlab软件中进行样条插值，可获得α∈(0,180°]区间范围内vop的连续函数及其曲线,分别如式(5)和图9所示。

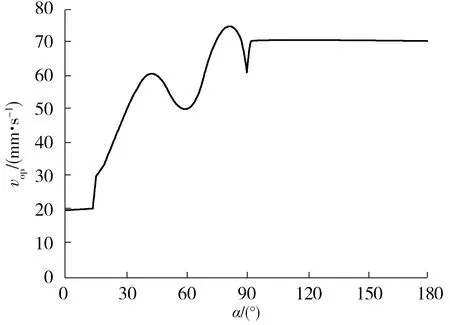
图9 最优填充速度连续函数曲线(A=B=0.5)

(5)

由式(5)可见，当拐角α∈(0,15°)时，vop均固定为20 mm/s，该最低速度可维持最基本的打印效率；当拐角α>90°时，vop均固定为70 mm/s。

2.4 拐角轮廓填充速度自适应控制的初步设计思路

要实现拐角轮廓填充速度的自适应控制，FDM程序应能提前识别喷嘴扫描路径上拐角轮廓特征并根据拐角大小自动计算最优填充速度。因此，程序设计的初步思路如图10示。首先，按照扫描路径顺序，合并同属一条直线的路径段并计算其长度L；其次，识别它是否为外轮廓，并计算外轮廓相连两段直线路径的拐角α；再次，根据产品的需求设定权重系数A和B，通过样条插值获得最优填充速度函数；接着，根据L值和α值，判断、计算和分配每一直线段路径的填充速度；最后，生成G代码供设备执行。其中，关于L值的判断存在两种情况：①每款FDM设备系统均对应其加减速运动路径段所需的最低临界长度值Lcritical，当L≤Lcritical时，填充速度默认为在加减速过程中变化，喷头执行加减速功能填充轮廓；②当L>Lcritical时，经历加速后的恒速值等于计算所得的最优填充速度值vop。

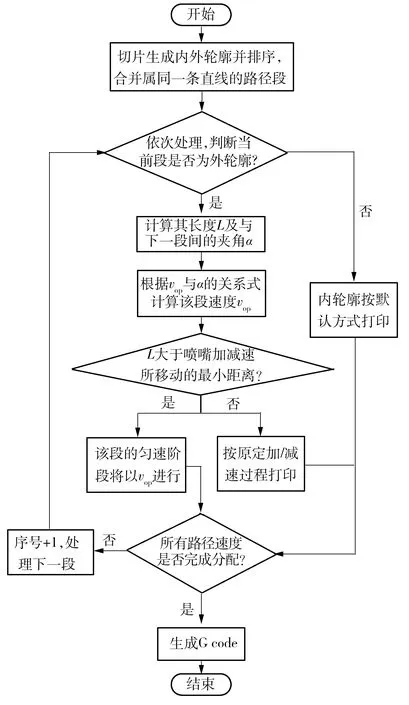
图10 拐角轮廓填充速度自适应控制程序流程图

3 结语

文中研究了拐角轮廓熔融沉积成型过程中填充速度与成形精度、打印效率之间的关系，结果表明：拐角轮廓的成形精度和打印效率均与填充速度有关；不同填充速度下拐角处的重复沉积区与漏沉积区实际面积之和均大于理论面积之和，且两者的差值随填充速度的增大而增大，拐角轮廓的成形精度与填充速度主要成反比关系；在低速区间(不大于50 mm/s)内填充速度越小成形精度越高、打印效率越低，反之亦然，但在高速区间内存在着高精度高效率打印的可能；效率方面，低速区间内打印耗时随着填充速度的增大而减小，但高速区间内打印耗时将逐步趋向于最低耗时，填充速度对打印效率的影响逐步减弱。

通过对成形精度和打印效率设定权重系数，借助样条插值法构建拐角轮廓最优填充速度连续函数，并嵌入到FDM系统G代码中，可实现填充速度的自适应控制，在保证拐角轮廓成形精度的同时兼顾打印效率。

除拐角轮廓外，文中研究思路与方法可应用于曲线轮廓FDM过程最优填充速度连续函数的构建。关于程序如何实现以及软硬件如何实施等，将在后续深入探讨。