合舍系统及其定理的能行证明
杜国平
(中国社会科学院 哲学研究所, 北京 100732)
本文拟基于括号表示法[1-4]以二元联结词“合舍”作为唯一初始联结词,建立一个命题逻辑自然推演系统;严格给出关涉定理证明的“化归”定义,进而探讨定理机械证明的能行性步骤。
一、形式语言
定义1 形式语言LDP包括如下两类符号:
(1)命题符号:p1,p2,…,pn,pn+1,…;
(2)联结词符号:「,」。
形式语言LDP中初始联结词只有一对左右括号“「」”。
定义2 形式语言LDP中的公式当且仅当有限次使用如下规则而得:
(1)单独的一个命题符号是公式;
(2)若符号串F、G是公式,则「FG」是公式。
通常以大写字母A、B、C等表示任意的公式。LDP中所有公式的集合记为Form(LDP)。
联结词「FG」的语义可用真值表直观表示如下(表1):
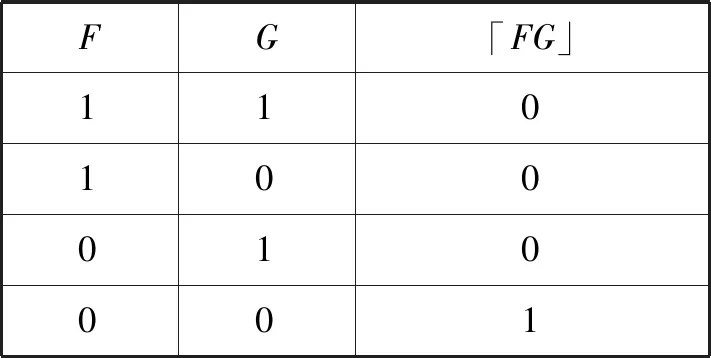
表1 联结词「FG」语义真值表
由此可见,「FG」就是F、G的合舍[5]。为了表达方便,定义引入如下一些缩写符号:
定义3
(A)=def「AA」
[AB]=def「「AA」「BB」」
『AB』=def(「(A)B)」)=def「「「AA」B」「「AA」B」」
命题1 联结词“「」”对于二值真值函数其表达能力是足够的。
二、公理系统
以合舍作为初始联结词的命题逻辑自然推演系统NPD1包括如下5条推理规则:
规则D1D├D。简记为Ref。
规则D2 如果Σ├D,那么Σ,Σ′├D。简记为+。
规则D3 如果∑,A├B,且Σ├「BB」,那么Σ├「AB」。简记为「」+。
规则D4 如果Σ,「CC」├「AB」,并且Σ,「CC」├A,那么Σ├C。简记为「」l-。
规则D5 如果Σ,C├「AB」,并且Σ,C├B,那么Σ├「CC」。简记为「」r-。
规则D1、规则D2是通常的命题逻辑自然推理规则。规则D3、规则D4和规则D5这3条规则是关于唯一联结词括号“「」”的特征推理规则,其中规则D3是括号“「」”的引入规则,规则D4、规则D5是括号“「」”的消去规则,规则D4是括号左消去规则,规则D5是括号右消去规则。
三、只含初始联结词“「」”定理的推演
定义4 公式A在系统NP1中由公式集Σ形式可推演,记为Σ├A,当且仅当Σ├A能由有限次使用规则SR1~规则SR5而生成。
引理1 若A∈Σ,则Σ├A。
该引理简记为∈。
引理2 若Σ├Σ′,且Σ′├C,则Σ├C。
该引理简记为⟹。
定理1 若Σ├A,且Σ├「AB」,则Σ├C。
证明:
1.Σ├A前提
2.Σ├「AB」 前提
3.Σ,「CC」├A1, +
4.Σ,「CC」├「AB」 2, +
5.Σ├C3,4,「」l-
对于定理1,特别地有:若Σ├A,且Σ├「AA」,则Σ├B。
定理2 若Σ,A├「CC」,且Σ,B├「CC」,则Σ,C├「AB」。
证明:
1.Σ,A├「CC」 前提
2.Σ,B├「CC」 前提
3.Σ,C,B├「CC」 2,+
4.Σ,C,B├C∈
5.Σ,C├「BB」 3,4,「」r-
6.Σ,C,A├「CC」 1,+
7.Σ,C,A├C∈
8.Σ,C,A├B6,7,定理1
9.Σ,C├「AB」 5,8,「」+
定理3 若Σ├「AA」,并且Σ├「BB」,则Σ├「AB」。
定理4 若Σ├「「AA」B」,则Σ├A。
证明:
1.Σ├「「AA」B」 前提
2.Σ,「AA」├「AA」 ∈
3.Σ,「AA」├「「AA」B」 1,+
4.Σ├A2,3,「」l-
定理5 若Σ├「AB」,则Σ├「BB」。
四、若干定义联结词“「」”定理的推演
定理6 若Σ├「「AA」「AA」」,则Σ├A。
证明:
1.Σ├「「AA」」 前提
2.Σ,「AA」├「「AA」「AA」」 1,+
3.Σ,「AA」├「AA」 ∈
4.Σ├A2,3,「」l-
根据定义3,该定理可以简记为:Σ├((A)),则Σ├A。
定理7 若Σ├A,则Σ├「「AA」「AA」」。
根据定义3,该定理可以简记为:Σ├A,则Σ├((A))。
定理8 若Σ├「AB」,则Σ├「BA」。
证明:
1.Σ├「AB」 前提
2.Σ,「「AA」「AA」」├「AB」 1,+
3.Σ,「「AA」「AA」」├「「AA」「AA」」 ∈
4.Σ,「「AA」「AA」」├A3,定理6
5.Σ├「AA」 2,4,「」l-
6.Σ,B,「AA」├「AB」 1,+
7.Σ├,B,「AA」├B∈
8.Σ├,B├「「AA」「AA」」 6,7,「」r-
9.Σ├,B├A7,8,定理6
10.Σ├「BA」 5,9,「」+
对于定理8,特别地有:若Σ├「「AA」「BB」」,则Σ├「「BB」「AA」」。根据定义3,这可以简记为:若Σ├[AB],则Σ├[BA]。
定理9 若Σ├「「AB」「AB」」,则Σ├「「BA」「BA」」。
证明:
1.Σ├「「AB」「AB」」 前提
2.Σ,「BA」├「BA」 ∈
3.Σ,「BA」├「AB」 2,定理8
4.Σ,「BA」├「「AB」「AB」」 1,+
5.Σ├「「BA」「BA」」 3,4,「」r-
根据定义3,该定理可以简记为:Σ├
定理10 若Σ├「「「「AB」「AB」」C」「「「AB」「AB」」C」」,则Σ├「「A「「BC」「BC」」」「A「「BC」「BC」」」」。
根据定义3,该定理可以简记为:Σ├<
以下,我们将<
定理11 若Σ├A,则Σ├「「AB」「AB」」。
根据定义3,该定理可以简记为:Σ├A,则Σ├
定理12
(1) 若Σ,「CC」├「AA」,则├,A├C;
(2) 若Σ,A├C,则Σ,「CC」├「AA」;
(3) 若Σ,A├「CC」,则Σ,C├「AA」;
(4) 若Σ,「AA」├C,则Σ,「CC」├A。
证明:
(1)
1.Σ,「CC」├「AA」 前提
2.Σ,A,「CC」├「AA」 1,+
3.Σ,A,「CC」├A∈
4.Σ,A├C3,4,「」l-
(2)(3)(4)类似可证。
根据定义3,该定理可以简记为:
(1) 若Σ,(C)├(A),则Σ,A├C;
(2) 若Σ,A├C,则Σ,(C)├(A);
(3) 若Σ,A├(C),则Σ,C├(A);
(4) 若Σ,(A)├C,则Σ,(C)├A。
定理13 若Σ,A├C,并且Σ,B├C,则Σ,「「AB」「AB」」├C。
根据定义3,该定理可以简记为:若Σ,A├C,并且Σ,B├C,则Σ,
定理14
(1) 若Σ├A,则Σ├「「AB」「AB」」;
(2) 若Σ├B,则(Σ├「「AB」「AB」」。
根据定义3,该定理可以简记为:
(1) 若Σ├A,则Σ├
(2) 若Σ├B,则Σ├
定理15 若Σ├A,且Σ├B,则Σ├「「AA」「BB」」。
证明:
1.Σ├A前提
2.Σ├B前提
3.Σ├「「AA」「AA」」 1,定理7
4.Σ├「「BB」「BB」」 2,定理7
5.Σ├「「AA」「BB」」 3,4,定理3
根据定义3,该定理可以简记为:若Σ├A,且Σ├B,则Σ├[AB]。
定理16 若Σ├「「AA」「BC」」,则Σ├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」。
证明:
1.Σ├「「AA」「BC」」 前提
2.Σ├A1,定理3
3.Σ├「「BC」「BC」」 1,定理5
4.Σ,A,B├「「AA」「BB」」 定理15
5.Σ,A,B├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」 4,定理14
6.Σ,A,C├「「AA」「CC」」 定理15
7.Σ,A,C├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」 6,定理14
8.Σ,A,「「BC」「BC」」├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」
5,7,定理13
9.Σ├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」 2,3,8,引理2
根据定义3,该定理可以简记为:Σ├[A
定理17 若Σ├「「「「AA」「BB」」「「AA」「CC」」」「「「AA」「BB」」「「AA」「CC」」」」,则Σ├「「AA」「BC」」。
根据定义3,该定理可以简记为:Σ├<[AB][AC]>,则Σ├[A
定理18 若Σ├「「AB」「AB」」,则Σ├「「A「「「AA」「AA」」「BB」」」「A「「「AA」「AA」」「BB」」」」。
根据定义3,该定理可以简记为:若Σ├
定理19 若Σ├「「A「「「AA」「AA」」「BB」」」「A「「「AA」「AA」」「BB」」」」,则Σ├「「AB」「AB」」。
根据定义3,该定理可以简记为:若Σ├
定理20 若Σ├「「「AA」B」「「AA」B」」,则Σ├「「「AA」「「AA」「BB」」」「「AA」「「AA」「BB」」」」。
根据定义3,该定理可以简记为:若Σ├<(A)B>,则Σ├<(A)[AB]>。
定理21 若Σ├「「「AA」「「AA」「BB」」」「「AA」「「AA」「BB」」」」,则Σ├「「「AA」B」「「AA」B」」。
根据定义3,该定理可以简记为:若Σ├<(A)[AB]>,则Σ├<(A)B>。
定理22 若Σ├A,则Σ├「「A「「AA」「BB」」」「A「「AA」「BB」」」」。
根据定义3,该定理可以简记为:若Σ├A,则Σ├
定理23 若Σ├「「A「「AA」「BB」」」「A「「AA」「BB」」」」,则Σ├A。
根据定义3,该定理可以简记为:若Σ├
定理24Σ├「「A「AA」」「A「AA」」」。
根据定义3,该定理可以简记为:Σ├
定理25 若Σ├「「A「AA」」「A「AA」」」,则Σ├「「「「A「AA」」「A「AA」」」B」「「「A「AA」」「A「AA」」」B」」。
根据定义3,该定理可以简记为:若Σ├
定理26 若Σ├「「「「A「AA」」「A「AA」」」B」「「「A「AA」」「A「AA」」」B」」,则Σ├「「A「AA」」「A「AA」」」。
根据定义3,该定理可以简记为:若Σ├<
定理27 若Σ├A,且Σ├「「「AA」B」「「AA」B」」,则Σ├B。
根据定义3,该定理可以简记为:Σ├A,且Σ├『AB』,则Σ├B。
定理28 若Σ,A├B,则Σ├「「「AA」B」「「AA」B」」。
根据定义3,该定理可以简记为:若Σ,A├B,则Σ├『AB』。
根据推理规则D1、推理规则D2、推理规则D4、定理27和定理28可知,系统NP1与通常的经典命题逻辑系统等价[6]。
根据定义3,公式「「「AA」「BB」」「「AA」「BB」」」既可以简写为([AB]),也可以简写为<(A)(B)>;公式「「「AB」「AB」」「「AB」「AB」」」既可以简写为(
因此,有:
定理29
(1) 若Σ├([AB]),则Σ├<(A)(B)>;
(2) 若Σ├<(A)(B)>,则Σ├([AB]);
(3)若Σ├(
(4) 若Σ├[(A)(B)],则Σ├(
定理30
(1) 若Σ├「AB」,则Σ├[(A)(B)];
(2) 若Σ├[(A)(B)],则Σ├「AB」。
定理31 令R{A}为任一包含A作为子公式的公式,R{B}为R中将所有A的出现替换为B而得的公式,则:
(1)Σ├R{「AB」},当且仅当Σ├R{[(A)(B)]};
(2)Σ├R{『AB』},当且仅当Σ├R{(「(A)B)」)};
(3)Σ├R{((A))},当且仅当Σ├R{A}。
五、公式的化归
受亚里士多德在三段论证明中所使用的化归思想的启发[7],我们可以将系统NP1中定理的证明通过化归来实现。
定义5 系统NP1中的化归规则仅包括如下7条:
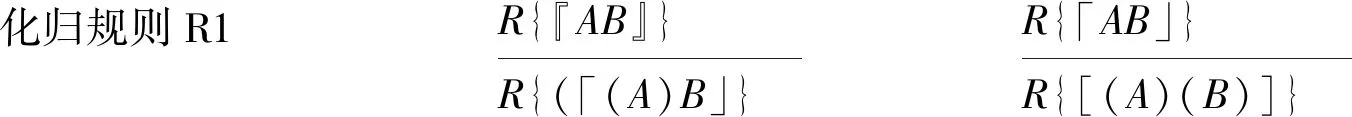
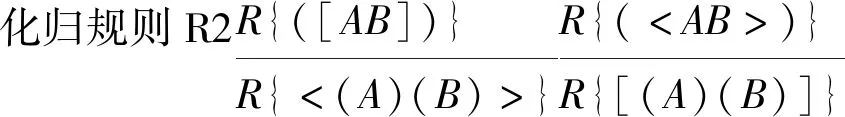
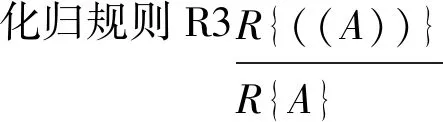
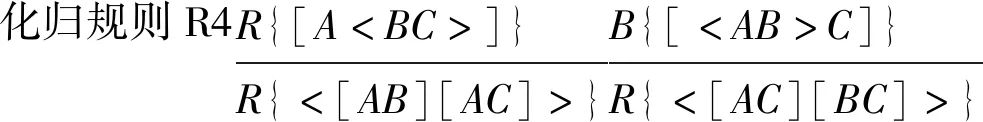
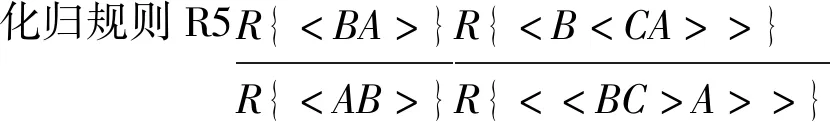
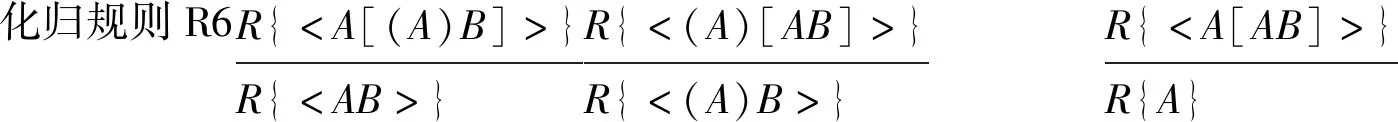
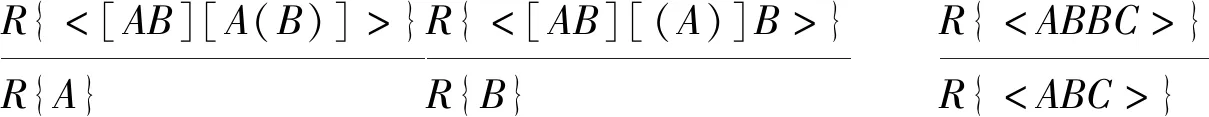
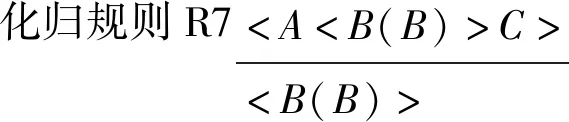
显然,前述定义和定理保证了上述化归规则的合理性。
对于包含初始联结词“「」”和定义联结词“( )”“[ ]”“< >”和“「」”的任一公式K0,如果它是系统NP1中的定理,可以按照如下程序纲要将其化归为
1.如果K0中含有符号“「」”和“「」”,使用规则R1将其中化归为一不含符号“「」”和“「」”的公式K1;
2.反复使用规则R2将K1化归为公式K2,使得“( )”只作用于原子公式或者原子公式前只含有若干个符号“( )”的公式之前;
3.反复使用规则R3将K2化归为公式K3,使得K3中原子公式之前的符号“( )”至多只含有一个;
4.反复使用规则R4将K3化归为公式K4,使得K4中符号“[ ]”符号只作用于若干原子公式或者只带有一个符号“( )”的原子公式;
5.反复使用规则R5将K4化归为公式K5,使得K5中符号“< >”之间的公式按照字母序和是否含有符号“( )”的顺序进行排列;
6.反复使用规则R6将K5化归为公式K6;
7.重复步骤5;
8.反复使用规则R7将K6化归为一
例如对于公式『
第1步:
(「(
([((
第2步:
<[(((A)))(((B)))]<((B))[(((B)))<((C))((A))>]>>
第3步:
<[(A)(B)]
第4步:
<[(A)(B)]
第5步:
<[A(B)][(A)(B)]B[(B)C]>
第6步:
<(B)BC>
第7步:
第8步:
因此,上述化归程序实际上为NP1中定理(上述已经证明的定理除外)的机械证明提供了一个能行性的方法。
不难发现,上述化归程序不仅提供了定理的机械证明程序,而且对于任意一个公式C,如果C能被化归为一个形如

