基于CEEMDAN方法和灰色模糊聚类的汇率预测研究

陈黎明，龙灵芝，郑千一

(湖南大学 金融与统计学院， 湖南 长沙 410079)

一、引言

汇率作为国家间货币兑换的比率，是国际贸易中不可或缺的重要组成部分，也是各国调节国际收支的重要手段之一。国家间的汇率大幅波动一方面会对贸易收支、经济增长和国际资本流动等宏观层面有重要影响；另一方面，对货币流通、物价水平和资源配置等微观层面也有广泛影响。自2005年人民币汇率制度再次改革以来，中国资本账户进一步开放，加速了人民币国际化进程，人民币逐渐成为与中国有密切经济往来国家的“货币锚”[1]。人民币汇率走势将影响经济主体预期，进而影响经济决策行为，若能对人民币汇率未来走势进行更为准确、合理的预测分析，将对微观主体的经贸活动、投融资决策和宏观经济的长期运行与调控具有重要现实意义。而汇率序列受外生因素的影响较大，波动特征呈现出明显的非线性、非平稳性和高噪声等特点，选取传统的时间序列分析方法往往具有较大的预测误差，难以准确捕捉汇率波动特征。因此，选取合适的模型对汇率进行准确预测一直是经济学领域需要深入研究的热点问题。

二、文献综述

国内外专家学者就汇率预测问题展开了广泛讨论和深入研究。早期的汇率预测主要利用单模型对汇率波动特征和波动趋势进行研究，其中具有代表性的有：Alex等利用双状态马尔科夫随机模型对美元汇率进行预测分析，实证结果表明相对于随机游走模型，该随机模型在汇率预测方面具有更为优良的性质[2]。余菊以2006年至2013年的1 771个人民币汇率日值高频数据为样本区间，创建GARCH模型对人民币与美元、港币、日元、欧元及英镑之间的汇率波动规律进行实证分析，实证结果表明人民币兑五大外汇币种汇率的波动具有长记忆性和明显的杠杆效应[3]。邓贵川等选取5种模型对2005年汇改后的人民币兑美元、欧元、日元和英镑4种主要国际汇率数据进行样本内模型拟合，再利用模型对汇率预期进行外推预测，研究发现，相较于其他汇率预测模型，汇率基本面模型的综合分析和预测能力更佳[4]。Ince等利用泰勒修正模型和传统货币模型对美元兑人民币、欧元等8种外汇数据进行了对比和综合分析，研究结果表明，泰勒修正模型预测精度较高[5]。江春等也基于拓展泰勒模型对影响汇率的因素进行分析，研究结果表明拓展的泰勒规则汇率模型对中国短期货币政策的传导和实施具有较强的理论解释力[6]。王全意等基于传统的M—F模型，以11个国家2000—2016年的相关数据为样本，实证分析人民币汇率变动与国际收支的关系，研究结果表明实际有效汇率可有效调节经常账户和资本与金融账户[7]。Cheung等将影子利率、风险及流动性因素纳入基于生产率的模型和“行为均衡汇率”模型中，并将这些模型的外推预测性能与随机可变窗口游走模型进行了比较，实证结果表明随机游走模型预测效果稍差[8]。李欣珏等构建了多元自适应可变窗算法，探测了汇率样本外推预测模型的最大化参数同质区间，实证结果表明，在中长期(3个月至24个月)的美元、欧元、英镑和日元兑人民币汇率的样本外推预测中，多元自适应可变窗算法能显著优于随机游走模型、购买力平价模型等模型[9]。

随着汇率研究进一步深入，部分学者开始采取分解集成策略对汇率进行分析，此外，由于神经网络(Neural Networks，简称NN)、支持向量机(Support Vector Machine，简称SVM)等机器学习方法具有较强的泛化能力，能够有效处理非线性问题，因而近几年来在汇率分析研究中得到广泛应用。王轩等采取先分解再综合泛化分析后采用综合集成的策略对人民币汇率进行实证分析，实证结果表明，基于支持向量回归的TEI@I集成预测模型不仅适用于线性问题分析而且适用于非线性问题分析，对于线性特征和非线性特征共存的人民币实际汇率也具有优异的综合分析能力[10]。王晓辉等基于独立成分分析(ICA)与BP神经网络理论相融合的多维时间序列预测模型对2008年以来的多维人民币汇率数据进行预测，研究表明IC—BP神经网络具有较好的预测精度[11]。黄山等基于BP神经网络的随机信号预测方法，以3种国际主要货币汇率的长期历史价格数据作为参考，对未来汇率价格走势进行短期预测，研究结果表明BP神经网络模型对汇率价格的预测精度较高[12]。Furao等基于改进的汇率预测深度信念网络(DBN)模型对3个汇率序列进行预测，实证表明，该方法在外汇汇率的预测方面，效果优于前馈神经网络(FFNN)模型[13]。Galeshchuk基于人工神经网络(ANNs)模型，对汇率(USD/EUR，JPN/USD，USD/GBP)的面板数据进行准确预测，实证表明，人工神经网络模型在汇率预测问题上表现优良[14]。Plakandaras等使用集成经验模态分解(EEMD)方法对原始汇率序列进行分解得到各分量序列，然后选取具有不同参数的支持向量回归机模型进行预测，实证分析结果表明，与其他单预测模型预测能力相比，SVR组合模型具有更强的样本内和样本外预测能力[15]。傅魁等分别利用单模型和MEEMD组合模型对欧元兑美元汇率序列进行实证预测和分析，研究结果表明MEEMD组合模型比其他单模型和EMD组合模型的短期预测能力和预测精度更好[16]。周晓波等对人民币汇率进行短期预测研究发现，GR_BP_Adaboost强预测模型相较于传统的ARMA、ARCH 和 GARCH 模型来说，具有更为优良的预测能力[17]。

综上所述，伴随汇率波动特征日趋复杂化，汇率预测模型逐渐从单一模型向组合模型转变，机器学习算法在汇率预测模型中的应用也日趋广泛，但当前文献主要集中在同类模型对比分析，将传统模型与机器学习算法优势相结合进行汇率预测研究的文献数量较少。因此，本文基于分解—重构—集成思想，构造CEEMDAN组合模型对人民币汇率进行预测。首先，利用CEEMDAN方法，将原始汇率序列分解为有限个本征模态分量(IMF)和一个残余分量；然后基于灰色模糊聚类法对各时频分量进行重构，得到高频项、低频项和趋势项，并选取不同的模型对重构项进行分析预测；最后，将各重构项预测结果进行集成，得到最终预测值。本文主要贡献包括以下几个：一是将目前在工程时频分析中广泛应用的改进时频分析方法CEEMDAN引入经济分析领域，尤其是汇率预测方面，从频域角度对汇率序列进行分解，揭示汇率序列在不同尺度下的波动特征；二是利用序列动态聚类方法——灰色模糊聚类，对各分量进行分类重构，从而得到高频项、低频项和趋势项；三是将传统时序模型ARIMA和机器算法(SVM、BP神经网络)相结合，增强模型的泛化能力，有效降低模型预测误差。

三、CEEMDAN组合模型

(一)基于CEEMDAN的汇率序列分解

自适应噪声的完全集成经验模态分解(Complete Ensemble Empirical Mode Decomposition with Adaptive Noise，简称CEEMDAN)方法由Torres等在2011年率先提出[18]。CEEMDAN方法通过在经验模态分解的每个阶段添加有限次的自适应白噪声，来降低重构误差和提高计算效率，有效解决了EMD方法中的模态混叠现象，还避免了EMMD方法计算量大和伪分量较多等问题，使得IMF分量的噪声幅值有效减小。

CEEMDAN方法中得到的模态分量必须同时满足两个基本条件：(1)在函数的有效区间内，局部极值点数目和过零点的个数之间的零点个数差值为一；(2)在任何时候，局部最大值和最小值的包络线必须为零。式中Ej(·)为未添加噪声因子前分解原始信号得到的第j个模态分量，wi为满足N(0,1)的高斯白噪声，x(t)为待处理的原始信号。

具体步骤如下：

1) 在原始信号x(t)中加入具有不同零均值单位方差的白噪声n(i)(t)，得到信号混合体x(i)(t)：

x(i)(t)=x(t)+n(i)(t)

(1)

其中，i为迭代次数i=1,2,…,m。

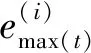
(2)

4) 重复步骤1)至步骤3)m次，可得第一个EEMD模态分量：

(3)

5) 在第一阶段(k=1)计算第一个残余分量：

r1(t)=x(t)-IMF1

(4)

6) 按照步骤2)至步骤5)分解每个r1(t)+ε1E1(wi(t)),(i=1,2,…,m)，得到第一个CEEMDAN模态分量，定义第二个CEEMDAN模态分量为：

(5)

7) 对于k=2,3,…,m，计算第k个残余分量：

rk(t)=rk-1(t)-IMFk

(6)

8) 按照步骤2)至步骤5)分解每个rk(t)+εkEk(wi(t)),(i=1,2,…,m)，得到第k个CEEMDAN模态分量，定义第k+1个CEEMDAN模态分量为：

(7)

9) 对于k+1，返回步骤7)，并重复步骤7)至步骤(9)，直到残余分量不满足IMF分量的要求时停止分解，最终的残余分量满足：

(8)

其中，m为分解得到的模态分量个数。给定的待处理信号x(t)可表示为：

(9)

(二)基于灰色模糊聚类方法的汇率序列重构

大量研究表明，汇率序列本质上由一系列波幅不一致的分量序列构成，这些序列分量大致可划分为高频项、低频项和趋势项三类，本文采用灰色模糊聚类法将关联度高且周期和波动频率相近的IMF分量合理地归为一类，重构高频项和低频项。

具体步骤如下：

1) 确定IMF分量的参考序列和比较序列

设定IMF分量的参考序列为ci(t)，比较序列为cj(t)，i=1,2,…,m;j=1,2,…,m，对各分量序列进行初始化处理：

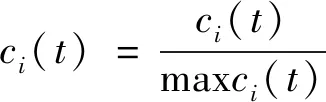
(10)

2) 计算IMF分量的灰色关联系数和灰色关联矩阵

灰色绝对关联系数的含义是被评价对象与参考对象进行绝对值比值比较，如果被评价对象与参考对象越接近，其绝对关联系数越接近1；反之，绝对关联系数越接近0。灰色绝对关联系数表达式为：

(11)

α为分辨系数，0≤α≤1，一般取α=0.5。

关联度是衡量一个采样子系统中两个因素或两个变量之间相似程度或接近程度的大小，一般通过计算各采样节点的算术平均数来衡量灰色关联度，但这样可能直接造成关联度信息的损失和影响局部点的关联序列测度值，从而影响整个灰色关联序列。本文借助灰色关联熵定理，利用熵值法赋予不同权重，加权计算关联度，具体表达式如下：

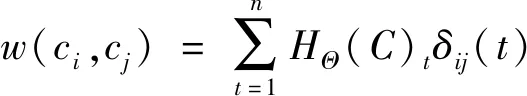
(12)

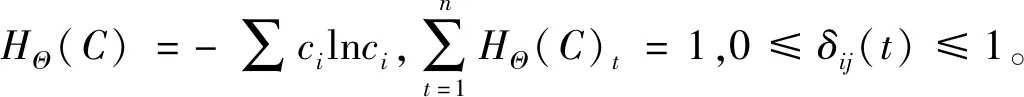
3) 构建模糊等价矩阵

基于步骤2)可得灰色关联矩阵，然后采用欧式距离法构造模糊相似矩阵Rm，再利用传递闭包法求解模糊等价矩阵。

传递闭包法必须满足以下3个条件：

①tc(R)是传递的；

②tc(R)⊇R；

③ 对于任何可传递的关系矩阵R′，存在R′⊇R，则tc(R′)⊇R。

4) 重构序列

根据模糊等价矩阵进行动态聚类，同时将IMF分量的波动频率和波动周期性纳入分析体系并选取合适的分类阀值，从而将IMF分量自然而然地划分成高频部分和低频部分，再将两者分别进行重构得到高频项和低频项。

(三)模型选取与创建

鉴于高频项、低频项和趋势项是由不同频度的分量重构得到的，所以三者的波动特征呈现显著差异，因而需要采用不同的方法对序列进行准确预测。BP神经网络具有多层前馈网络，在训练过程中，以误差为依据进行反向传播算法训练。一般利用梯度下降算法进行样本训练，这种方法跟纠错学习规则比较接近，权值在性能函数梯度的反方向进行迭代，能够进行各种非线性映射，并以任意精度接近任意非线性反方向传播函数，处理高频数据在性能上具有显著优势，因此运用BP神经网络对高频项进行分析预测。支持向量机(SVM)是一种基于数据结构风险最小化原则的非线性映射和回归方法，本质上是将低维空间的非线性问题投射到高维特征空间，将非线性问题转化为线性问题，然后再利用线性方法进行分析。大量文献表明，SVM方法在低频项的非线性预测和分析能力问题上呈现出较为优良的性质，故SVM方法成为对低频项进行分析预测的不二选择。趋势项波动较为平缓，呈现出较为显著的线性特征，故选取ARIMA模型进行分析预测。下面对BP神经网络、SVM方法和ARIMA模型做进一步阐述：

1.BP神经网络

BP神经网络(Back-ProPagation Network)又称反向传播神经网络， 由Rumelhart等[19]率先研究提出，是对非线性可微函数进行权值模拟训练的多层神经网络。该输出预测算法中数据信息参量前向反馈传输，而数据运算误差反向传递。学习过程中采用最速梯度下降法，即各层函数的权值根据误差函数的负梯度方向迭代更新，直到误差项足够小，故本文选用BP神经网络模型对高频项的复杂性进行拟合预测。基于样本数据本身的波动特征和区间特点，本文选取的BP神经网络结构为4-4-1。神经网络模型中传递函数为Tansig，训练函数为Trainlm，权重和阀值的系统性学习算法以及性能函数分别为Learngdm和Mse。此外，模型的目标误差设定为1×10-6，最大迭代次数设定为1 000次。具体训练过程如图1所示。

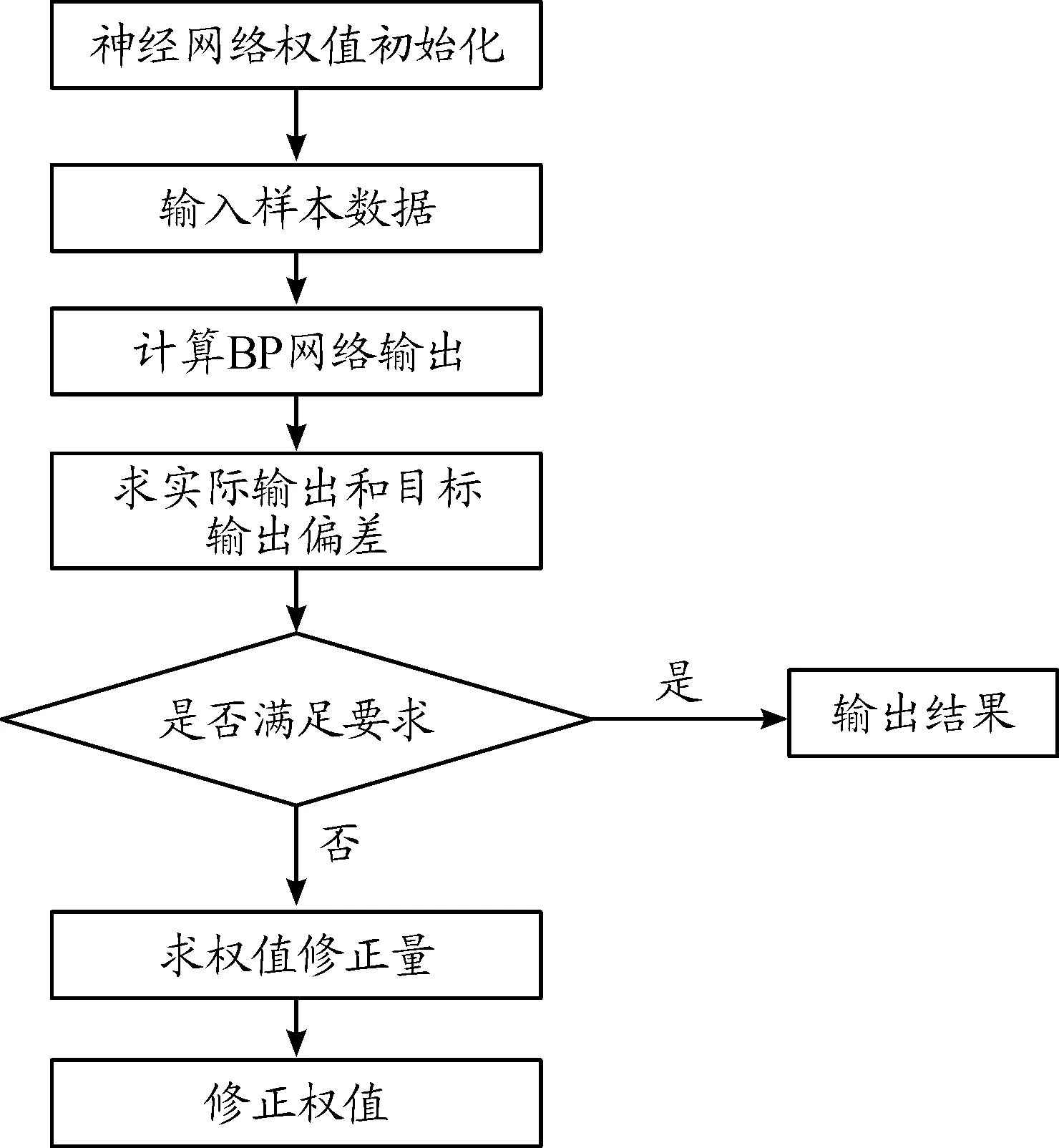
图1 BP神经网络算法训练过程

2.SVM方法

SVM(Support Vector Machine，简称 SVM)方法最初由Vapnik[20]提出，算法在学习过程中以结构化风险最小为准则。对于低维空间线性不可分情况，SVM使用内机核函数将低维空间线性不可分的样本投射到高维空间使其线性可分。低频项的波动频率虽然较低，但仍具有明显的非线性特征，利用一般的多项式进行拟合得到的模型误差大且效率较低。而利用SVM对样本进行训练，可大大提升运算效率。此外，SVM能够有效克服过拟合的问题，泛化能力强。

核函数作为SVM方法的核心，是决定算法性质优劣的关键部分。常用核函数有多项式核函数、径向基核函数、线性核函数。其中，径向基核函数属于非线性映射的核函数，且通常只有一个需要进行合理调整的参数s(核宽度)，故只需要合理地选择错误代价参数便可用于任意分布的样本。本文采用径向基核函数对低频项进行处理和分析预测。

3.ARIMA模型

ARIMA(Autoregressive Integrated Moving Average Model，简称ARIMA)模型由美国统计学家Box G E P和英国统计学家Jenkins G M于1970年提出[21]。ARIMA模型的核心步骤是差分运算，借此实现非平稳时间序列的平稳化过程，再建立模型进行分析预测。模型ARIMA(p,d,q)基本结构如下：

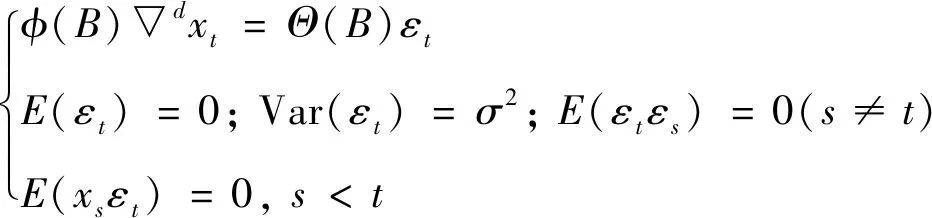
(13)

其中，p为模型的自回归阶数，d为数据的差分次数，q为移动平均阶数，Θ(B)是移动平滑系数多项式，φ(B)是自回归系数多项式，▽d=(1-B)d，{εt}是零均值白噪声序列。

4.CEEMDAN组合模型创建

基于分解—重构—集成策略，CEEMDAN组合模型的创建过程大致可以分为3步：一是利用CEEMDAN方法对汇率原始序列进行有效分解，得到有限个IMF分量和一个残余分量；二是基于灰色模糊聚类思想对序列分解后的分量进行重构，得到高频项、低频项和趋势项；三是根据各重构项的波动特征分别选取合适的模型进行外推预测，重构得到的高频项、低频项和趋势项分别利用BP神经网络、SVM方法和ARIMA模型进行预测，最终的预测结果由各项的预测值集成得到。

CEEMDAN组合模型创建的过程如图2所示。

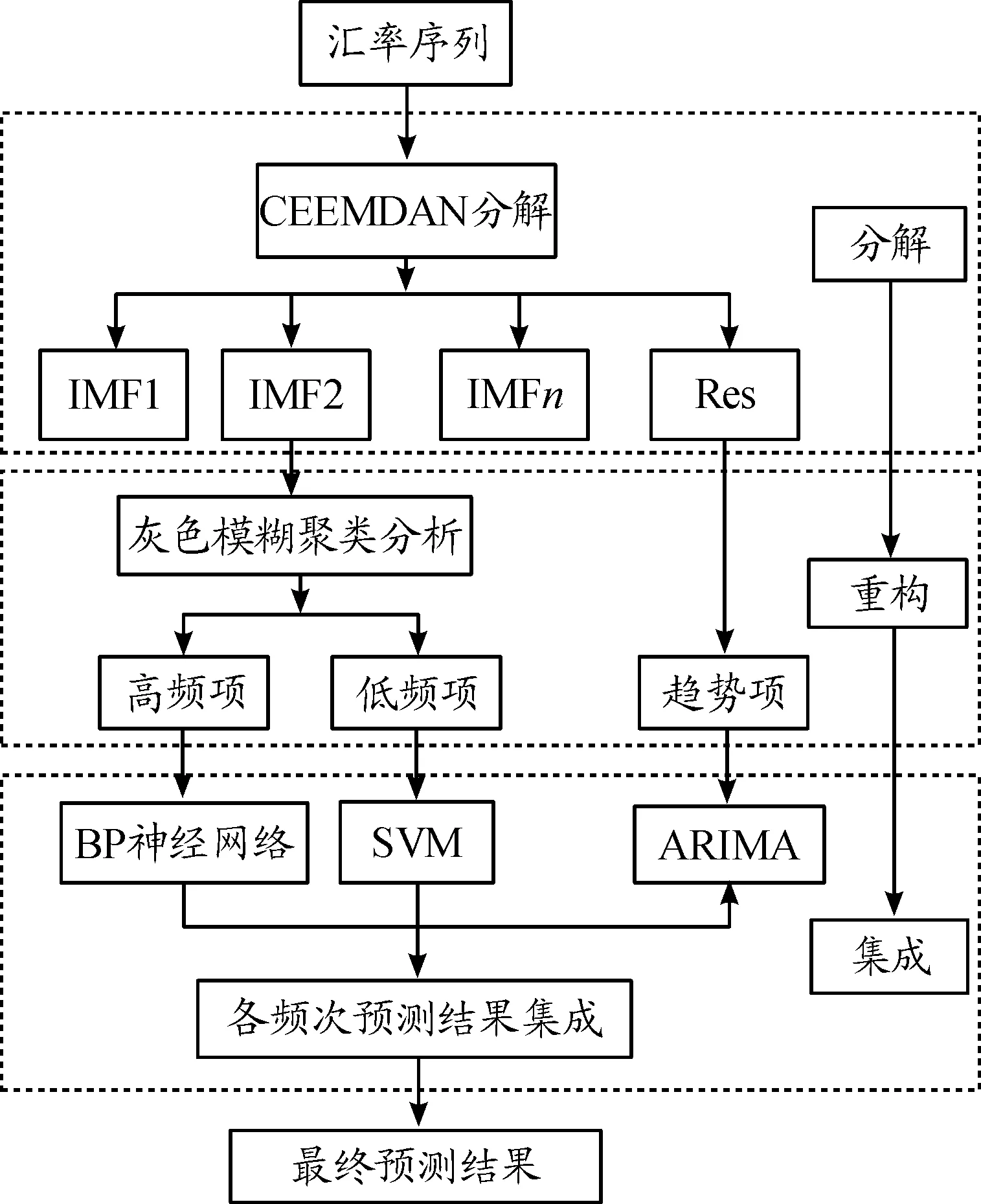
图2 CEEMDAN组合模型框架

四、汇率预测实证研究

(一)汇率原始序列特征判别

本文研究样本为2019年1月2日至2019年11月28日的人民币兑美元汇率中间价数据(数据来源于国家外汇管理局)。剔除节假日后共222个原始数据，选取不同模型对2019年12月2日至2019年12月31日(排除节假日共22天)的汇率进行预测。首先对汇率原始序列进行非线性、非平稳性、尖峰厚尾性以及长记忆性检验，具体结果如表1所示。

由表1可知，BDS检验在5%的显著性水平下，p值均为0，拒绝原假设，即认为原始序列具有非线性。ADF检验中，p值为0.392，不能拒绝原假设；KPSS检验中，t统计量的值为3.849，大于检验临界值0.463，拒绝原假设，即汇率原始序列具有非平稳性。JB检验中，p值为0，拒绝原假设，表明汇率原始序列不满足正态性假设，即具有尖峰厚尾特征。R/S分析中，Hurst指数为0.638(大于0.5)，故汇率原始序列存在长记忆性。

表1 原始序列性质检验

(二)汇率原始序列多尺度分解

汇率原始序列经EMD、EEMD和CEEMDAN分解后的结果分别如图3、图4和图5所示。

图3 汇率原始序列的EMD分解结果

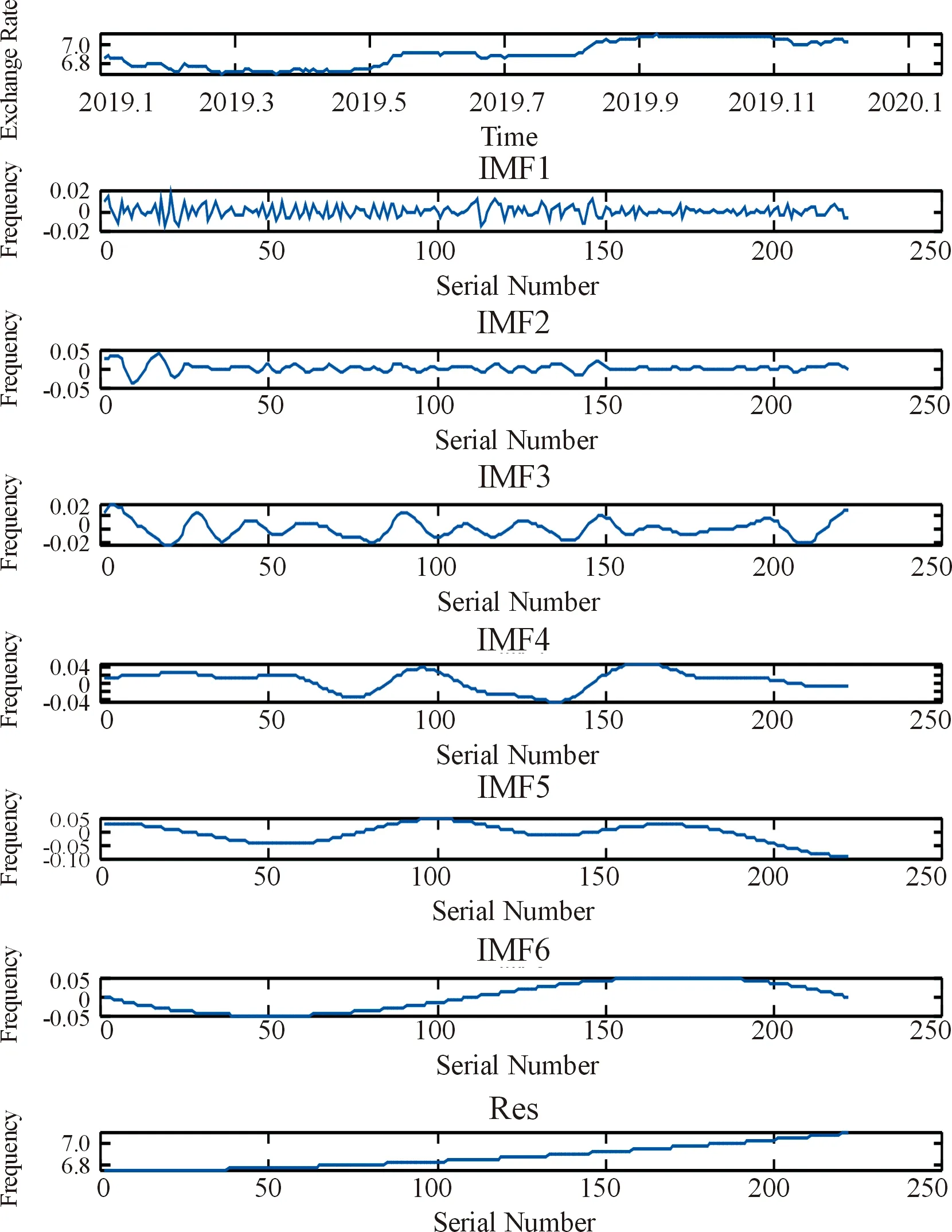
图4 汇率原始序列的EEMD分解结果

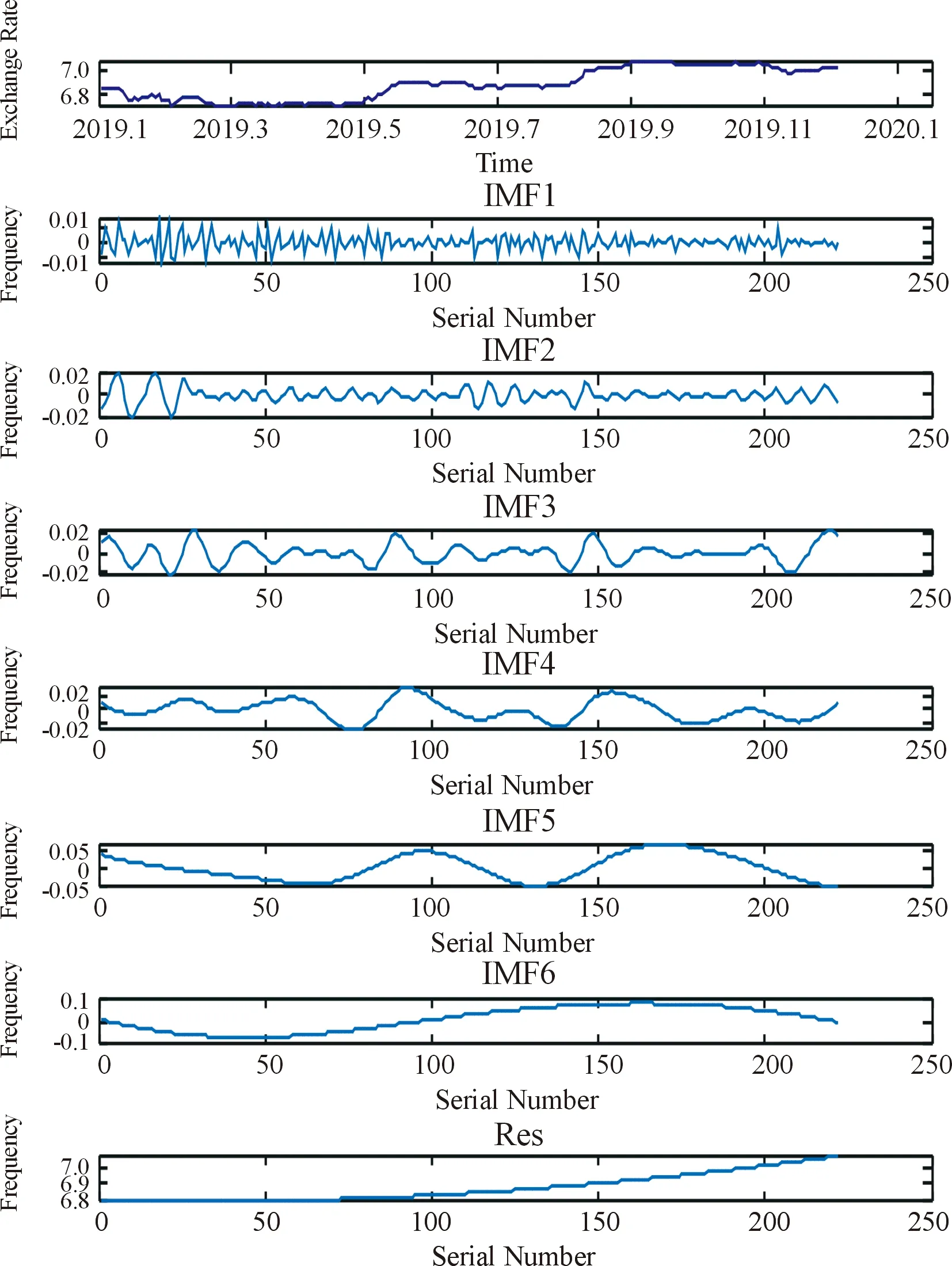
图5 汇率原始序列的CEEMDAN分解结果

通过分解，展现了汇率原始序列的组成结构和多尺度特征。对比可知，CEEMDAN方法的分解效果最佳。各IMF分量和残余分量的频率水平和振幅具有显著差异，表明不同的分量序列间存在较大差异，需选取不同模型进行分析预测。

(三)分量序列重构

基于模糊等价矩阵，对序列分解得到的各IMF分量进行动态聚类。考虑到每个IMF分量的波动特征和分量之间的关联度，IMF分量可分为{IMF1、IMF2、IMF3、IMF4}和{IMF5、IMF6}两类(如图6所示)，将第一类重构为高频项，第二类重构为低频项。绘制原始汇率序列和各重构项(高频项、低频项和趋势项)的走势图(图7)。

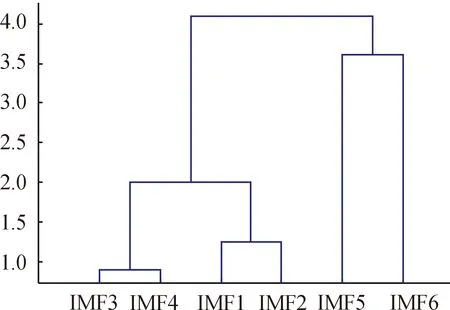
图6 IMF分量灰色模糊聚类

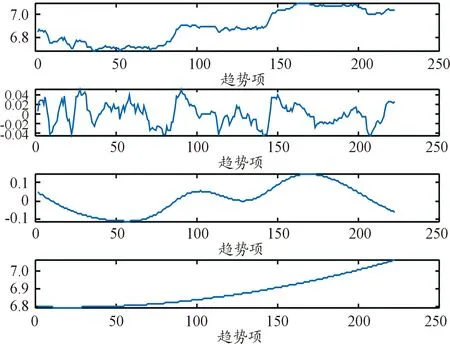
图7 汇率原始序列和各重构项走势

为进一步分析高频项、低频项和趋势性的统计性质，选取平均周期、Pearson相关系数和方差比3个指标进行统计和分析。平均周期用来刻画每个序列的平均波动周期，利用快速傅氏变换(Fast Fourier Transformation，简称FFT)计算序列的平均波动周期；Pearson系数用来刻画各分量序列与原始序列之间的相似程度；方差比则用来刻画各分量序列方差值与原始序列方差值之间的相对比重，体现了分量序列对原始序列的方差贡献度。统计分析结果如表2所示。

表2 汇率序列与重构序列的统计分析

由表2和图7可知，高频项、低频项和趋势项的波动特征呈现出显著差异，这表明不同尺度下影响汇率波动的因素也不尽相同。首先，从高频项来看，平均周期为31.71天，周期相对较短，一定程度上表明高频项对汇率的长期走势影响甚微；Pearson相关系数为0.026，表明高频项和原始汇率序列的波动特征存在显著差异，相似度较低；方差比为2.69%，说明高频项对原始汇率序列的贡献率很低。总的来说，高频项对汇率总体波动的影响非常小。从前文绘制的走势图来看，高频项波动非常不稳定，即便短周期内，波动也较为显著，反映了汇率短期内的非均衡特征。该现象主要受相对利率、外汇市场供需、政府干预、市场投机行为等一系列因素的直接影响，是汇率市场的正常周期性波动，并不会影响汇率的基本波动走势。其次，从低频项的周期性来看，平均波动周期为222天，相对较长，反映出低频项对汇率的影响较大；Pearson相关系数为0.862，表明低频项和汇率序列的相似度较高，序列波动走势较为一致；方差比为30.34%，说明低频项对原始汇率序列的贡献率较大。最后，从趋势项来看，无明显周期性特征；Pearson相关系数为0.901，表明在一定条件下，可充分利用趋势项来刻画原始汇率序列的基本波动走势；方差比为66.97%，进一步表明趋势项是原始汇率序列的主体成分，可较为准确地描绘出汇率的较长时间内的基本波动走势。趋势项整体走势较为平缓，表明在中短期内，汇率即使受到一些重大事件或某些政策的影响，而产生一定程度的波动幅度，但这些波动对汇率的中短期整体走势影响很小，汇率波动仍将集中于趋势线附近的一个小区间内。

(四)集成与预测

不同的波动特征，宜选取不同的预测模型，从而进一步提高整体预测精度。对于高频项，选取BP神经网络模型进行分析预测；对于低频项，选取SVM模型进行分析预测；对于趋势项，可以看出明显的线性变化特征，故选取ARIMA模型进行分析预测。利用上述模型得到各重构项的预测值后，再对各预测值进行集成，便可得到最终的预测值。

为了检验CEEMDAN组合模型的准确性和预测性能，将模型预测结果与ARIMA、SVM、LM-BP神经网络等单模型，以及ARIMA-SVM、EMD组合模型和EEMD组合模型的预测结果进行对比分析。本文选用MAE、MSE、MAPE和MSPE四项误差指标来准确衡量各模型的预测精度，各模型预测误差如表3所示。

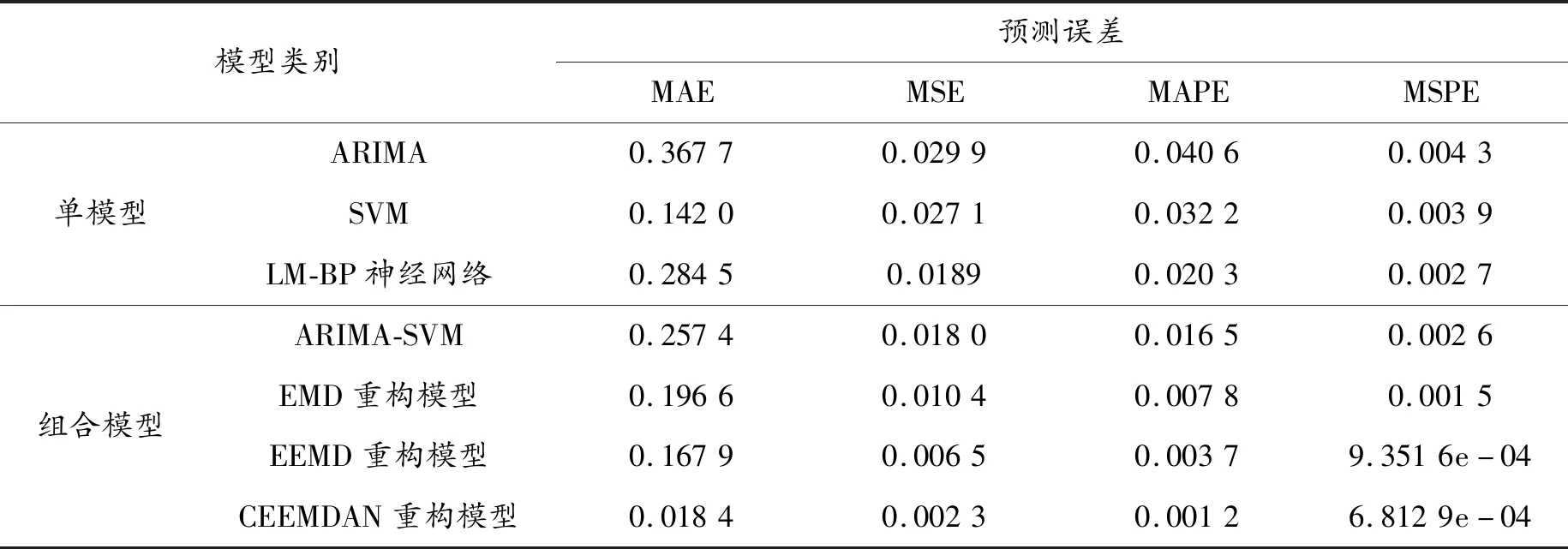
表3 不同模型的预测误差

为进一步对比模型对汇率序列走势的预测效果，绘制2019年12月2日至2019年12月31日的原始汇率序列走势和各组合模型预测汇率走势对比图，如图8所示。

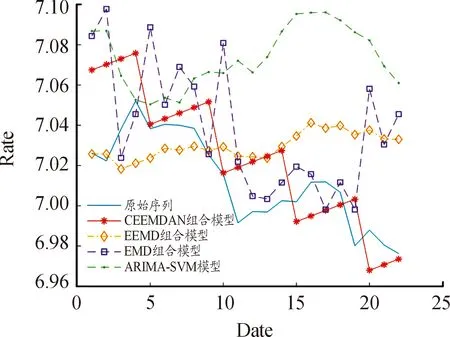
图8 原始汇率序列和组合模型预测序列走势

表3给出了各模型的预测误差，组合模型预测误差明显低于单模型。从单模型来看，无论是从绝对误差指标(MAE和MSE)分析，还是以相对误差指标(MAPE和MSPE)作为衡量依据，ARIMA模型的预测误差均最大。若以MAE作为衡量指标，LM-BP神经网络模型的预测误差为0.284 5，而SVM模型预测误差为0.142 0，LM-BP神经网络模型的预测精度低于SVM模型。究其原因，MAE是绝对误差指标，当预测值中一旦存在异常点，则可能造成较大的偏差。基于此，将相对误差指标(MAPE和MSPE)纳入考量体系，实证表明LM-BP神经网络模型预测误差低于SVM模型。结合各指标分析结果可知，单模型中，ARIMA模型的预测误差较大，而LM-BP神经网络模型预测误差较小。从组合模型来看，重构的组合模型的预测误差明显低于ARIMA-SVM组合模型，尤其是EEMD组合模型和CEEMDAN组合模型，两模型在绝对误差指标MSE下的预测误差远小于ARIMA-SVM模型和EMD组合模型，甚至不在同一精度分位数。结合图8分析可知，ARIMA-SVM模型预测序列走势与原始汇率序列走势虽较为贴合，但是偏离原始汇率序列较远，无法准确预测汇率值，使得模型整体预测误差较高。在相对误差指标MAPE和MSPE下，EEMD组合模型的预测误差分别为0.003 7和9.351 6×10-4，CEEMDAN组合模型的预测误差分别为0.001 2和6.812 9×10-4，故CEEMDAN组合模型预测精度更高。分析图8中CEEMDAN组合模型预测序列与原始汇率序列走势可知，CEEMDAN组合模型能够较为准确地捕捉汇率序列预期走势的拐点，对整体走势刻画较为准确，从而使得模型整体预测误差较低。 总体而言，单模型对汇率序列的分析和预测效果不及组合模型，而在组合模型中，CEEMDAN组合模型预测效果更优。

此外，从理论上来看，由于汇率序列具有非线性、非平稳性和长记忆性等波动特征，影响了模型的预测效果，其中，ARIMA模型的预测效果远远不如SVM模型和BP神经网络模型。组合模型中，CEEMDAN组合模型的预测和分析效果最佳，这是因为EMD组合模型和EEMD组合模型中在进行序列分解时存在模态混叠、计算量大以及伪分量等复杂问题，降低了汇率序列的分解效率，进而直接影响到最终的汇率序列预测和分析效果，而CEEMDAN组合模型在分解时采用CEEMDAN方法，该方法通过在经验模态分解的每个阶段添加有限次的自适应白噪声对EEMD方法进行优化，降低了重构误差，提高了计算效率，使得模型整体的预测误差最小；而ARIMA-SVM模型预测误差较大，则是因为该组合模型虽然能够利用ARIMA模型和SVM模型分别对汇率序列中的线性特征显著部分和非线性特征显著部分进行预测，但由于线性和非线性特征混叠严重，影响了模型的预测效果。

五、结论

本文针对汇率序列的非线性、非平稳性和长记忆性等特点，基于分解—重构—集成策略通过构建CEEMDAN组合模型对人民币兑美元汇率序列的波动特征进行准确刻画并利用模型进行样本外推预测，对汇率短期走势进行预判分析。实证研究表明相较于单模型和其他组合模型，CEEMDAN组合模型的预测效果最佳，其主要具有3项特点：第一，CEEMDAN方法克服了EMD、EEMD方法中模态混叠、运行效率不佳等缺点，能够更加准确对汇率序列进行分解，从而清晰地展现汇率序列在不同尺度下的波动特征。第二，采用灰色模糊聚类法对IMF分量进行重构，一方面能够避免直接对各分量进行预测的运算量大问题；另一方面，在灰色模糊聚类过程中引入灰色关联熵赋权，使得高频项和低频项的重构更为准确客观。第三，高频项、低频项和趋势项具有不同的波动特征，采用单一方法难以保证预测精度，而有针对性地选取不同的方法进行组合预测，可有效提升整体预测精度。

综上所述，本文构建的CEEMDAN组合模型在汇率预测方面具有良好的理论分析性能，一方面有利于深入理解汇率波动的本质特征和规律性；另一方面有助于对人民币兑美元汇率的未来短期走势进行准确预测。与此同时，该模型为数据驱动型算法，不仅适用于人民币汇率的预测，而且适用于其他宏观经济变量的分析和预测，适用范围较广。

在未来的研究过程中，如何利用CEEMDAN组合模型对包括汇率在内的宏观经济变量进行分析仍然有许多有意义的研究方向。如汇率区间长度增大时，是否需要对汇率序列进行结构性判断，然后分阶段对汇率序列进行预测，最后加权集成；对于离散型数据，将其连续化后再利用CEEMDAN模型进行预测是否妥当；如何拓展模型的应用领域等等，都是需要进一步研究的问题。