三维测力装置维间耦合效应试验及解耦方法

张益瑞 苏建 徐观

(吉林大学 交通学院，吉林 长春 130022)

刚度和阻尼等是转向架悬挂系统重要的性能参数，决定车辆的动力学性能[1- 4]。但由于悬挂零部件质量和实际装配状态的差异，悬挂参数实际值与设计值有所偏离，而转向架装配状态下的试验测量值更为可靠，如何科学准确地完成悬挂参数的试验获取成为行业研究热点[5- 6]。转向架试验台正是基于这一现实需求而开发的专用台架系统，可以实现转向架悬挂系统参数的精准测定[7- 8]。在参数测定试验过程中，要求进行悬挂系统的变形和载荷测量，变形测量多使用标准化的位移传感器，载荷测量则缺少适用的现成产品，因此，研制多维载荷测量的专用高性能测量设备成为必然。

近年来，多维载荷测量技术不断进步[9- 10]，Dwarakanath等[11- 12]开发了Stewart类型多维力传感器，但其结构复杂、标定难度大；吴强等[13- 14]开发了方柱式、整体四柱式、十字梁式等不同结构的多维力传感器，此类产品多存在抗偏心能力差、抗侧向力能力差及测量结果受载荷加载位置影响大等难以解决的缺点。多维载荷测量技术的另一个难点在于传感器测量的维间解耦，王国泰等[15]提出采用分段线性解耦方法；Mach等[16]针对分布式三维电场测量方式，通过求解输出信号与电场分量的关系矩阵及其逆矩阵实现解耦。随着技术的发展和成熟，基于人工智能的非线性解耦方法得到了广泛应用，姚斌等[17]采用多层前馈神经网络成功实现了对手术机器人多维力传感器的解耦。需要说明的是，解耦方法的解耦效果和传感器结构密切相关，在工程实践中最合适的方法需要通过必要试验来确定。本文基于转向架试验台的结构形式及试验需求，设计了采用多个力传感器并联布置的三维测力装置，借助于专用的标定设备完成静态标定试验，研究其三维载荷测量的维间耦合效应并提出基于最小二乘法和BP神经网络的解耦方法；最后，通过单轴加载试验及三轴加载正交试验验证了两种解耦方法的有效性，解决了转向架悬挂参数测定试验的载荷测量问题，具有重要的应用价值和现实意义。

1 三维测力装置的结构及原理

1.1 转向架试验台简介

转向架试验台是吉林大学根据中车长客股份有限公司生产和科研实际需求开发的，能够完成车辆/转向架参数测定，以及模拟车辆运行工况的轨道车辆专用多功能试验设备。如图1所示，转向架试验台作为一个完整的试验系统，由控制系统、液压油源系统、测量系统、机械系统等子系统组成。控制系统接收试验运动谱指令数据并实时控制试验台完成相应试验动作。液压油源系统是试验台的动力来源，提供工作压力21 MPa、流量3 500 L/min的可调液压动力。测量系统用于试验对象目标物理量的实时测量与记录，包括激光传感器(测量位移量或者变形量)、三维测力装置(测量三向载荷)以及相应的数采设备。机械系统作为试验台的主体构成，是决定其试验功能的物理基础，由试验台基础、试验辅助工装以及3套相互独立的6自由度运动子系统组成。各子系统协调配合，提供符合要求的多自由度、持续加载、全程受控、精准高效的试验条件。

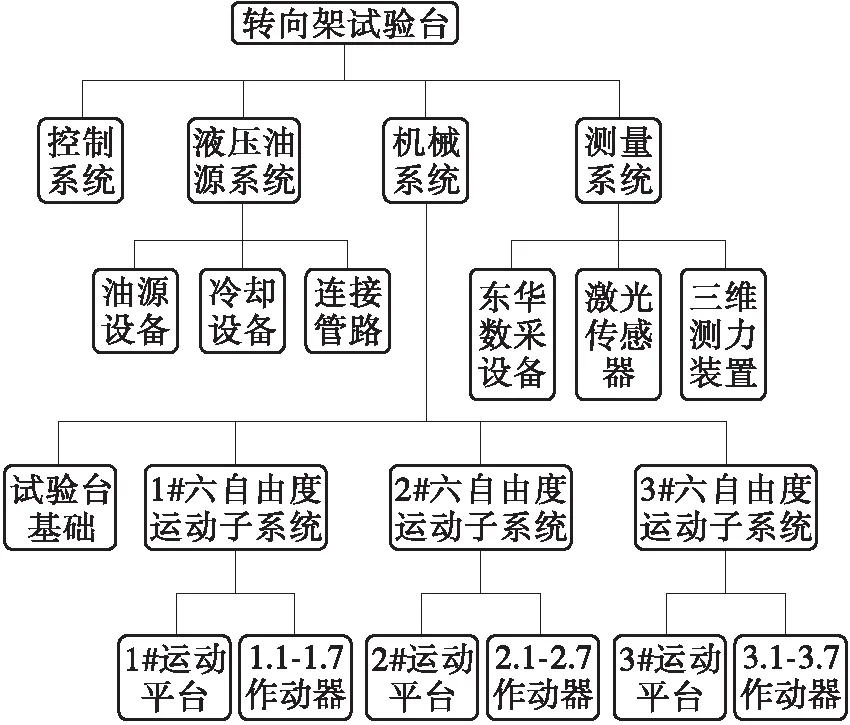
图1 转向架试验台系统组成示意图

图2所示为转向架试验台机械系统模型。试验台机械系统包括3套成品字形分布的运动平台：1#运动平台位于上方，与试验转向架枕梁固定连接，用于枕梁加载及车体空间运动模拟；2#运动平台和3#运动平台位于下方，与试验转向架轮对固定连接，用于轮对加载及轨道激振模拟。每套运动平台都由正交安装的7台液压作动器(4台垂向作动器、两台纵向作动器和1台横向作动器)驱动，通过活塞杆的伸长量控制，能够独立实现3个方向的平动和转动，共6个自由度的运动，也可以完成3套运动平台的协调控制，共18个自由度的运动。

图2 转向架试验台机械系统模型图

1.2 三维测力装置结构

转向架试验台对载荷的测量是一个难点，虽然液压作动器均安装有力传感器来测量轴向力，但是试验中作动器通过运动平台对转向架加载，这种非接触的间接驱动方式决定了使用作动器自带力传感器难以直接测量载荷，尤其是对于转向架试验台这种多作动器联合驱动的多自由度运动试验台架，其载荷之间具有强耦合性，液压作动器轴向力和试验转向架的实际受载关系复杂。因此，液压作动器自身的力传感器不能作为载荷测量的有效手段。

根据转向架试验台的试验需求，特设计专用的三维测力装置，用于三向载荷的测量。图3所示为三维测力装置的结构模型，三维测力装置由底座、台板、测力传感器以及附属线缆组成，台板和底座之间无接触，通过对称分布在台板/底座四角处的4个测力传感器连接，台板与底座若有相对位移，测力传感器则会产生相应变形。

图3 三维测力装置结构模型图

图4所示为三维测力装置的安装实景，三维测力装置底座通过螺栓固定连接在运动平台上表面，台板以专用的轮对卡具固定连接试验转向架轮对。

图4 三维测力装置安装图

1.3 三维测力装置测量原理

作为三维测力装置的测量元件，测力传感器的核心构成是弹性体，弹性体的结构形状及应变片的贴片、组桥方式决定三维测力装置的测量精度。本质上，三维测力传感器属于切应力传感器或者剪切梁传感器，以切应力来测量外界负载的方式消除了正应力测量存在的缺点(如对载荷的作用位置比较敏感、精度不高、抗偏载能力弱等)。传感器弹性体为组合式结构，整体加工，基座为四方环型结构，中心为圆柱形销柱，弹性体基座通过固定螺栓连接三维测力装置底座，销柱及装卡段用于连接台板。

(1)

通过上述计算，当传感器弹性体受3个方向的加载力时，在相应的测量位置均产生与加载力呈线性关系的切应力。切应力在实际中难以测量，但切应力会引起与中心轴线成45°角的正应变，梁中性面上各点均为纯剪切受力状态，取任意一点分析，图5所示为所取点正方形的微体变形示意，由以下几何关系求得切应变γ和与轴线成45°角的正应变ε±45°的关系。

(2)

同理，

(3)

又

(4)

式中：G为剪切模量；E为弹性模量；μ为泊松比。

图5 中性面正方形微体变形示意图

从而得到外载荷F与正应变ε45°的关系：

(5)

对于确定的材料和尺寸，当梁受到外载荷作用时，会产生与外载荷呈线性关系的、与中心轴线成45°角的正应变，正应变可以通过应变片测量，从而计算出相应的外载荷。因此，测力传感器的应变片贴片方向应与测量载荷成45°角。

以X轴载荷的测量为例，图6给出了应变片贴片模型。测量X方向载荷的应变片为Sx1-Sx4，位于与XZ平面平行的弹性体贴片段表面，并且其方向均与Z方向成交叉45°角。

应变片的工作原理是应变效应，即导体或半导体材料在外界力的作用下变形时，其电阻值产生相应的与变形量呈线性关系的变化，这种电阻变化非常微小，一般通过搭建惠斯通电桥完成测量。

图6 X轴载荷测量应变片贴片模型图

三维测力传感器X轴载荷测量电路为四臂差动式全桥电路，RSx1-RSx4分别是应变片Sx1-Sx4的初始电阻值，Us为电桥供电电压，则电路的输出电压为

(6)

设定应变片选用同种规格，灵敏系数为KR，则

(7)

式中，εSx1-εSx4为应变片Sx1-Sx4的应变值。

此外，根据受力分析，

εSx1=εSx3=εSx

(8)

εSx2=εSx4=-εSx

(9)

式中，εSx为应变片Sx1、Sx3的应变值，拉伸时为正、压缩时为负。

从而得到

U0=UsKRεSx

(10)

综上所述，通过设计应变片的测量位置及布桥方式，可以使得电桥电路的输出电压与应变片所测量应变呈特定的线性关系，从而达到测量载荷的目的。

2 三维测力装置维间耦合效应

2.1 三维测力装置静态标定试验

经上述分析，当三维测力装置装配完成后，需要通过静态标定试验来寻求电压和载荷的特定关系。设定三维测力装置的三轴载荷测量值矩阵与测量电路输出电压值矩阵满足公式:

Fm×3=Um×3K3×3

(11)

式中：Fm×3为三轴载荷测量值矩阵；Um×3为三轴输出电压值矩阵；K3×3为标定系数矩阵，代表三维测力装置测量值与测量电路输出电压值之间的数值关系；m为数据值序列数，代表数据取样规模。

标定系数矩阵是三维测力装置精度的重要保障，需要通过标定试验尽可能准确地寻求其数值，并探究不同方向载荷测量值之间的耦合关系。

选取一台三维测力装置进行标定试验，图7所示为标定试验现场。将三维测力装置的底板固定到标定平台上，按照特定顺序放置标定砝码来施加垂向载荷。为减小偏载，特在三维测力装置台板上放置砝码支撑框架，标定时砝码支撑框架的质量要考虑在内，同时通过两个水平正交布置的千斤顶对三维测力装置台板进行手动加载，垂向载荷的数值通过标定砝码的组合方式计算得到，水平载荷的数值通过与千斤顶串联的力传感器测量得到。

图7 三维测力装置标定试验现场图

使用东华测试技术股份有限公司的DH5922动态信号测试分析系统，实时采集三维测力装置测量信号值，并通过1394接口与计算机通讯，实现数据采集、处理及标定系数的设定。

图8所示为三维测力装置分别在X、Y、Z轴单轴单向标定试验中的电压输出，图中绘出了载荷与相应轴测量电路输出电压值的趋势线及拟合方程表达式。单轴加载时，加载轴所对应测量电路有线性度良好的电压输出，但非加载轴电路同时有较小的电压输出，表明三维测力装置受任一轴向载荷时，三轴测量电路均有电压输出，即存在传感器的维间耦合效应。

若忽略维间耦合效应，假定测量电路电压输出仅线性相关于自身轴向的载荷，则标定系数矩阵K1为对角矩阵，将图中趋势线斜率取倒数即可得到标定矩阵：

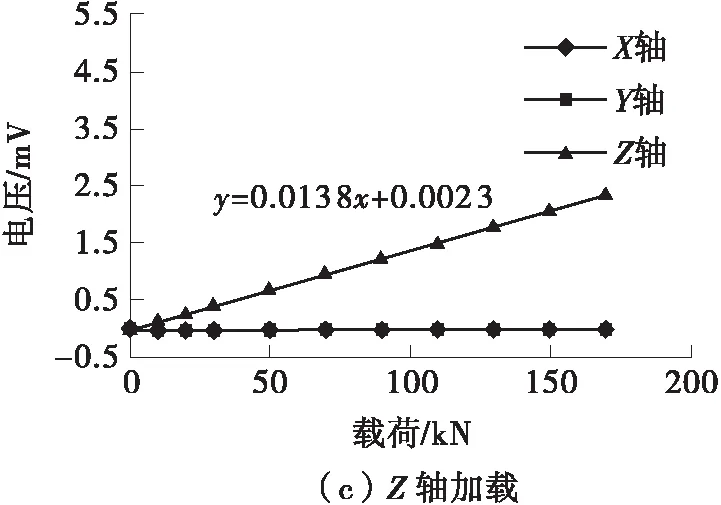
图8 三维测力装置标定数据图

(12)

2.2 维间耦合效应试验

多维传感器的维间耦合效应从产生原因上一般分为结构性耦合与误差性耦合：结构性耦合是由于传感器的一体化整体构造而形成的，某一方向的载荷必然会引起其他方向的变形，使应变片产生非期望数值；误差性耦合的根源是制造工艺、贴片方式以及应变片的性能差异等非确定因素，具有明显的个体特性。

为分析维间耦合效应，设定三维测力装置不同轴间的耦合度Cij，来表示i轴输入载荷时j轴的测量输出值与期望输出值的差值相对于i轴测量输出值的百分比大小，即

(13)

式中：Foj为j轴测量输出值；Fej为j轴期望输出值；Foi为i轴测量输出值。

标定系数矩阵设定为K1，进行单轴加载试验。对三维测力装置X轴正向加载，载荷依次为30、60、90、120、150 kN，实时记录三维测力装置在试验过程中的三轴载荷测量值，图9所示为三维测力装置X轴加载三轴耦合效应分析。由于通过千斤顶手动加载，三轴测量值时域曲线中X轴测量值在不同载荷之间平滑过渡，Y/Z轴测量值以及X轴与Y/Z轴的耦合度数据均匀分布在整个测量值范围内。

图9 X轴加载维间耦合效应分析

X轴正向加载时，Y轴产生了正向的类似线性偏移，XY耦合度CXY为正且较为稳定；X轴正向加载时，Z轴产生了负向线性偏移，XZ耦合度CXZ为负且同样较为稳定，但是XZ耦合度CXZ比XY耦合度CXY的绝对值大，说明X轴正向加载时对Z轴的影响程度比对Y轴的大。

类似地，对三维测力装置Y轴和Z轴分别进行正向加载，图10和图11为对应耦合效应分析。

Y轴正向加载时，X轴与Z轴测量值均产生了正向偏移，X轴偏移线性度较好，其耦合度CYX为正且较为稳定，Z轴偏移线性度较差，其耦合度CYZ为正，但是随着Y轴载荷的增加，耦合度CYZ逐渐减小，说明Y轴正向加载时对X轴和Z轴产生同方向的影响，但是随着Y轴载荷的持续增加，对X轴的影响保持稳定，对Z轴的影响逐渐降低。

图10 Y轴加载维间耦合效应分析

图11 Z轴加载维间耦合效应分析

Z轴正向加载时，对X轴和Y轴产生规律性较差的影响，但是其耦合度均匀分布在零附近，且数值均不大，说明Z轴正向加载对X轴和Y轴的影响程度均较小。

上述试验说明，作为试验对象的这台三维测力装置，Z轴正向加载对X轴测量值和Y轴测量值的影响较小，但X轴和Y轴加载时，对Z轴测量值的影响却较大，并且影响效果相反。通过对其他几台三维测力装置进行相同试验，发现对于每一台三维测力装置，三轴之间的耦合效应缺乏严格的一致性和规律性，这也验证了误差性耦合的个体差异特性。

3 三维测力装置解耦方法及验证试验

维间耦合效应会降低多维传感器的测量精度，应尽量消除或者削弱其不利影响，常用方法有物理解耦和数值解耦。物理解耦要求传感器具有更科学的结构和更优秀的贴片工艺，数值解耦则需对测量结果进行数值修正，在实际应用中应综合使用。本文将最小二乘法和BP神经网络两种常用方法应用于三维测力装置的数值解耦，并通过验证试验进行解耦效果对比。

3.1 最小二乘法数值解耦方法

使用最小二乘法进行线性拟合，标定系数矩阵K2的计算如下:

K2=(UTU)-1UTF

(14)

计算标定系数矩阵K2：

(15)

与不考虑维间耦合效应时相比较，标定系数矩阵K2不再是对角矩阵，说明三维测力装置每一轴的载荷测量输出均受到其他轴载荷的影响，标定系数矩阵起到了数值上的解耦作用。

3.2 BP神经网络数值解耦方法

三维测力装置的维间耦合效应有明显的非线性特征，最小二乘法数值解耦将其载荷测量值在数值上表示为三轴应变片测量电路电压值的特定线性组合，有一定的局限性，如解耦不彻底或效果不稳定。相比之下，BP神经网络解耦方法具有更理想的非线性解耦效果，应用广泛。将三维测力装置作为三输入三输出系统，在Matlab环境下搭建BP神经网络，图12所示为三维测力装置的BP神经网络模型，包括输入层、隐含层和输出层共3层。输入层3个节点对应三轴输出电压值U，输出层3个节点对应三轴载荷测量值F。隐含层为单层结构，理论证明单个隐含层的网络可以通过适当增加神经元节点的数目来实现理想的非线性映射，但隐含层节点数没有特定公式计算，依据实践经验并结合模拟试验，本文选用隐含层节点数为5。W1和W2分别为输入层到隐含层以及隐含层到输出层的权重矩阵，b1和b2分别为隐含层阈值矩阵和输出层的阈值矩阵，a1为隐含层输出矩阵，网络隐含层传递函数选择logsig函数，输出层传递函数选择purelin函数。

图12 BP神经网络模型

网络中相邻两层节点通过权值连接，这些权值参数代表网络的非线性映射特性，根据输入、输出标准值采用迭代方式确定，图13所示为BP神经网络训练误差(e)迭代曲线，迭代次数(n)达到485时，均方误差降低至0.1的指标，训练结束，将神经网络模型导出作为三维测力装置的解耦程序参数。

图13 BP神经网络误差迭代曲线

3.3 解耦验证试验

重复进行单轴正向加载试验，分别采用最小二乘法和BP神经网络完成数值解耦，图14所示为单轴加载时的解耦效果分析。无论是采用最小二乘法还是采用BP神经网络，解耦后各轴的耦合度均有大幅度的下降，并且在整个区间内波动不大，说明这两种方法都有明显的解耦效果。相比最小二乘法，BP神经网络的解耦效果更好，但两者差别较小，说明三维测力装置的维间耦合效应非线性不显著，两种数值解耦方法均是有效的。

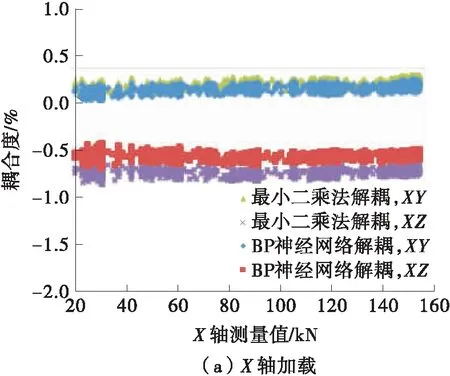
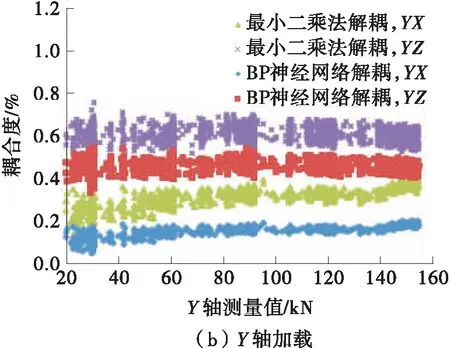
图14 解耦效果分析图

在试验台的实际应用中，三维测力装置通常采用三轴加载，因此，有必要考察这种工况下三维测力装置的测试精度。文中采用正交实验法，选用三因素四水平正交实验表，表1所示为三维测力装置三轴加载载荷测量值统计。对三轴独立的测量误差eX、eY、eZ和三维测力装置整体测量误差eS进行计算，整体测量误差的计算根据下式：

(16)

表1 三轴加载载荷测量值统计表Table 1 3-D force measuring platform orthogonal test data

分析试验数据发现：X轴和Y轴载荷对自身轴的测量有相同趋势的影响，测量误差会随着载荷的增大而增大；X轴和Y轴载荷对Z轴的测量同样有相同趋势的影响，Z轴测量误差会随着X轴和Y轴载荷的增大而增大；Z轴载荷对X轴和Y轴的测量没有特定影响，这与前述单轴加载时各轴之间的耦合影响结果一致。无论是单轴测量误差还是整体测量误差，都没有超过1.5%，满足试验测试的实际需求。两种解耦方法对比发现，BP神经网络解耦的测量误差更优，但是效果并没有很明显的提升(整体测量误差最值从1.50%提升到1.38%)，说明对于三维测力装置，采用最小二乘法和BP神经网络进行数值解耦均可以实现满足工程要求的解耦效果。通过对其他几台三维测力装置的试验，发现每台三维测力装置都有自身的差异性，这要求进行大量的重复性试验来对每一台三维测力装置进行个体化标定，使得标定工作变得重复繁琐但不可或缺。

综上，文中所述三维测力装置达到了设计要求，是成功的专用试验设备，推而广之，多维测力传感器的维间耦合效应可以减弱，却难以消除，以标准化、规范化的生产制造装配工艺加上科学有效的解耦方法，能够满足现代工程的测量要求。

4 结论

(1)三维测力装置采用多个切应力传感器并联布置，应变片粘贴方向与测量载荷方向成45°角，测量电路为四臂差动式全桥电路，测量电路输出电压与载荷有确定的线性关系。

(2)任一轴载荷均会在所有测量电路引起输出电压，加载轴测量电路输出电压与载荷线性度较好，非加载轴测量电路输出电压值较小并且与载荷关系具有不确定性，即存在多轴力传感器的维间耦合效应。

(3)基于最小二乘法和BP神经网络的数值解耦方法，均能够减小三维测力装置测量维间耦合度，有效提高测量精度。

(4)三轴加载正交试验表明，通过最小二乘法和BP神经网络实现数值解耦后，三维测力装置的单轴测量误差和整体测量误差都不超过1.5%，其测量精度满足测试的实际需求。