欠驱动起重机的神经网络直接鲁棒自适应控制

程文明 张道裕 谌庆荣 翟守才

(西南交通大学 机械工程学院∥轨道交通运维技术与装备四川省重点实验室,四川 成都 610031)

桥门式起重机因负载能力强、场地利用率高、操作灵活、通用性强等优点而被广泛应用于生产和物流环节中。桥门式起重机系统的独立控制量数目少于系统自由度[1- 2]，为典型的欠驱动系统，其欠驱动特性给控制带来了难度。吊重通过钢丝绳与起重小车相连，起重小车到达目标位置后吊具及吊重会存在一定程度的残余摆动，这使得货物难以精确定位，不但降低了工作效率，而且带来了安全隐患。因此，对桥门式起重机防摇摆控制策略的研究具有现实意义。

总体而言，起重机的防摇摆控制策略可分为开环控制和闭环控制两大类[3]。开环控制不依赖小车位置、吊重摆角等系统运行中的实时参数的获取，控制系统结构简单，但其往往需要精确的系统模型才能实现良好的控制效果，一般鲁棒性较差。针对起重机防摇摆的开环控制方法主要有输入整形控制和离线轨迹规划等。文献[4]提出一种经优化算法优化的阶跃输入加速度函数，通过优化算法保证系统对钢丝绳绳长变化具有较低的敏感性，一定程度上解决了传统输入整形技术鲁棒性较低的问题；文献[5]采用相平面分析法研究3种起重机小车加速度曲线对吊重残余摆动的影响，得到一种基于吊重等效能量控制的起重机小车动态加速度运动轨迹曲线；文献[6]针对具有复杂双摆效应的起重机系统提出一种解析轨迹规划方法，将轨迹规划问题转换为凸优化问题，能保证小车定位和摆动抑制的双重控制目标。闭环控制依赖小车位置、吊重摆角等系统运行中的实时参数的反馈，控制系统较复杂，但具有较好的鲁棒性。针对起重机防摇摆的闭环控制方法主要有PID控制、自适应控制和滑模控制等。文献[7]提出一种新型轨迹跟踪方法，先对起重机动力学方程进行部分反馈线性化，随后进行一系列坐标变换，在此基础上构造非线性控制器;文献[8]提出了一种具有滑模控制结构的增强PD控制器，滑模部分用于构造控制器框架，PD部分用于稳定系统，控制器设计不依赖系统参数，控制效果较好且鲁棒性强；文献[9]提出一种新型自适应分层滑模控制器，其方法可以使固定的滑模表面处于活动状态以搜索状态轨迹，进而使系统状态尽快进入所需的滑动表面，跟踪精度高，鲁棒性强；文献[10]针对三维桥式起重机模型提出基于滑模控制(SMC)的鲁棒有限时间防摇摆跟踪控制方法，分别实现了位置跟踪、防偏和防摆控制，控制器能适应系统参数及初始条件的变化；文献[11]针对旋转起重机防摆问题提出含非线性滑模面的控制算法，非线性滑模面带来的系统可变阻尼比使得系统具有较快的响应速度与较小的超调，防摆控制效果良好。

随着智能算法的发展，模糊理论、神经网络等展现出对未知非线性函数的拟合能力，这为系统参数完全或部分未知的起重机系统控制提供了新思路，出现了智能算法与传统控制理论结合下的新型控制器。文献[12]针对集装箱起重机的防摇摆控制，利用模糊算法设计滑模控制的控制器增益，有效避免了系统抖振的出现；文献[13]将PID控制和神经网络补偿结合在一起，使得系统能在取得较小的稳态误差的情况下依然保持良好的瞬态性能，为线性PID控制器增益选择提供新思路；文献[14]提出一种纯神经网络自适应轨迹跟踪控制器，控制器输入仅需要小车位置及速度信息，无需模型信息，跟踪效果良好；文献[15]提出了一种塔式起重机神经网络滑模防摆控制方法，利用RBF(径向基函数)神经网络输出逼近系统的不确定项，并运用遗传算法优化滑模控制器的参数，系统控制性能良好。

本文针对二维双摆桥门式起重机的防摇摆轨迹跟踪控制问题，提出一种基于RBF神经网络的直接鲁棒自适应控制算法。该算法利用RBF神经网络能以任意精度逼近未知复杂非线性函数的特性[14- 17]，使用其构造控制器输出，随后基于Lyapunov理论证明了目标控制器作用下系统的稳定性，最后通过仿真实验验证了方法的有效性与鲁棒性。

1 双摆桥门式起重机动力学建模

桥门式起重机实际模型较为复杂，进行起重机动力学建模时需对其进行简化，本文在合理的范围内做出以下假设：①模型为二维，仅考虑吊重与吊钩在小车运行方向上的摆动；②不考虑空气阻力；③不考虑吊重的起升与下降以及钢丝绳变形，视钢丝绳长为常数；④吊钩及吊重视为质点；⑤吊钩与吊重在平衡点附近摆动；⑥起重小车质量有界；⑦仅考虑作用于起重小车的系统外界扰动，且扰动有界。

简化后的起重机模型示意图如图1所示，其中x为小车位置；θ1、θ2分别为吊钩和吊重摆动角度；mt、mh、mp分别为小车、吊钩、吊重质量；l1、l2分别为小车与吊钩间、吊钩和吊重间钢丝绳长度；u为控制输出；d(t)为作用于小车上的有界外界随机扰动；g为重力加速度。取系统广义坐标q=[xθ1θ2]T，根据第二类拉格朗日能量方程构造的系统动力学微分方程如下[9]：

(1)

图1 二维双摆桥门式起重机模型简图

由于假设吊钩及吊重是在平衡点附近摆动的，故摆角θ1、θ2较小，可做如下线性化简化[14]：

(2)

将式(2)代入式(1)可得：

(3)

2 控制器设计

2.1 RBF神经网络结构

RBF神经网络结构简单，泛化能力强，研究表明其能以任意精度逼近未知非线性函数[14- 17]。图2所示为n-m- 1结构的RBF神经网络，网络有3层：输入层、隐含层和输出层。隐含层神经元激活函数为径向基函数，形式如下：

(4)

式中：X=[x1x2…xn]T,为网络的输入；cj为隐含层第j个神经元高斯基函数中心向量，与输入向量同维；bj为隐含层第j个神经元高斯基函数宽度。

RBF神经网络权值为

w=[w1w2…wm]T。

RBF神经网络隐含层输出为

h=[h1h2…hm]T。

RBF神经网络输出为

y=wTh=w1h1+w2h2+…+wmhm

(5)

图2 RBF神经网络结构图

2.2 控制律设计

由式(3)可得：

(6)

对跟踪误差函数s求时间的一阶导数可得：

(7)

不考虑外界扰动时，引入跟踪误差函数s构造鲁棒项，可设计理想控制律如下：

(8)

式中，η为正常数。

将理想控制律代入式(7)得：

(9)

不考虑系统参数未知及外界扰动的情况下，构造系统Lyapunov函数如下：

(10)

对L*求时间的一阶导数可得：

(11)

u*=w*Th(X)+ε

(12)

(13)

因理想控制律设计未考虑外界扰动影响，为使系统在外界扰动作用下仍保持稳定，需要设计合适的神经网络权值自适应律，文中神经网络权值自适应律取

(14)

式中，γ为自适应增益，γ>0，δ>0。

2.3 控制律的稳定性证明

将控制律式(8)、(12)、(13)代入式(7)可得：

(15)

(16)

对L求时间的一阶导数得：

(17)

将权值自适应律代入式(17)，得：

(18)

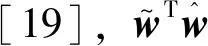
(19)

由基本不等式可得：

(20)

将式(19)、(20)代入式(18)，可得

(21)

(22)

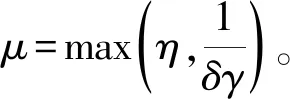
夜色已经降临，万花谷里灯火繁盛，空气里满是初荷与金合欢花交会的清甜香气，小鲲金声玉振地长吟，载着四人往高高的摘星楼飞去，摘星楼之上，暮紫的回光里，灿灿长庚星领着群星正在冉冉浮现。

解不等式(22)可得：

(23)

(24)

3 仿真与分析

3.1 跟踪轨迹选取

为评估上文所提出的小车控制律的控制效果，需要选取一个能使小车快速、平稳到达目标位置的理想轨迹来验证其跟踪性能，本文小车运行轨迹的选择参考文献[14,20- 21]，轨迹表达式如下：

(25)

式中，pd为目标位置参数；ka、kv分别为最大容许加速度与最大容许速度参数；ϑ为轨迹初始加速度参数。文中取pd=20，ka=0.5，kv=3，ϑ=5。

3.2 控制器参数设置

3.3 对比实验与分析

为验证本文所提出的基于RBF神经网络的直接鲁棒自适应控制器(下文简称DRAC)的控制性能，利用Matlab Simulink对其进行仿真，同时取Ouyang等[9]提出的一种自适应分层滑模控制器(下文简称AHSMC)作为参照，其控制律如下：

(26)

(i=1,2,3)

控制器增益具体取值如下：λ1=0.01，λ2=0.01，η′=8，κ=440，δ′=44。

假定对照实验控制对象为同一起重机，目标起重机基本参数如下：mt=1 000 kg，mh=100 kg，l1=2 m，l2=1 m。

选取工况1和工况2进行DRAC和AHSMC的对比实验，其中工况1的mp=500 kg，工况2的mp=5 000 kg。

取零初始状态下的系统进行仿真验证，定义θ1res、θ2res为吊钩、吊重在小车到达目标位置后10 s内的最大残余摆角。对比实验仿真结果见图3-6和表1。

由对比实验仿真结果可知，工况1下，DRAC与AHSMC对目标轨迹的跟踪效果都比较好，小车到达预定位置后吊钩与吊重残余摆动较小，系统能快速进入稳定状态。两控制器作用下的控制器输出(控制力)、吊钩残余摆角、吊重残余摆角相似，但DRAC的最大小车位置跟踪误差较小，两控制器的最大跟踪误差分别为0.001 7和0.010 5 m，且DRAC使跟踪误差收敛于0 m的表现优于AHSMC；工况2下，DRAC仍能保持良好的跟踪效果，小车最大位置跟踪误差及吊钩、吊重残余摆动较小；AHSMC的跟踪效果有一定的下降，小车最大位置跟踪误差较工况1由原先的0.010 5 m增长到0.181 1 m，增加较多，吊钩及吊重分别存在0.463°和0.466°的残余摆动，其控制效果在吊重增加后有一定的削弱。

图3 工况1的跟踪效果对比图

图4 工况1的控制力及防摆效果对比图

图5 工况2的跟踪效果对比图

图6 工况2的控制力及防摆效果对比图

表1 DRAC和AHSMC对比实验仿真结果Table 1 Simulation results of comparative experiment of DRAC and AHSMC

结合上述仿真结果，对比AHSMC，DRAC具有如下优势：①控制器设计不需要具体系统参数值，仅需要小车位置及速度信息作为控制输入，不需要摆角信息的实时反馈，整体控制器结构较为简单；②控制效果随系统参数变化无明显改变，鲁棒性较强。

3.4 鲁棒性实验与分析

工况1、2的仿真结果表明DRAC对吊重的变化具有较强的鲁棒性，为进一步探究起重机系统参数及外部随机扰动对DRAC控制效果的影响，取如下几个工况进行仿真分析。

工况3：mt=2 000 kg，mh=200 kg，mp=5 000 kg，l1=2 m，l2=1 m。

工况4：mt=1 000 kg，mh=100 kg，mp=5 000 kg，l1=1 m，l2=2 m。

工况5：mt=1 000 kg，mh=100 kg，mp=5 000 kg，l1=2 m；l2=1 m，d(t)=100 sintN。

以工况2为参考，工况3探究小车及吊钩质量变化对控制器控制效果的影响，工况4探究钢丝绳长变化对控制器控制效果的影响，工况5探究外界随机扰动对控制器控制效果的影响，且定义的随机扰动为幅值100 N的正弦波函数。DRAC鲁棒性实验结果见图7-8和表2。

由DRAC鲁棒性实验结果可知，工况3、4、5下，DRAC都对目标轨迹具有较好的跟踪效果。小车位置跟踪误差、吊钩残余摆角、吊重残余摆角这些能体现跟踪性能和防摆效果的参数在鲁棒性实验的几个工况下比较稳定。控制力随具体工况不同而略有波动，小车位置跟踪误差不超过0.006 4 m，吊钩、吊重运行过程中摆动不超过3.127°，残余摆动不超过0.045°。由此可得出：本文提出的基于RBF神经网络的直接鲁棒自适应控制器具有较强的鲁棒性，可被应用于各种类型起重机、各种工况下起重机的防摇摆控制。

图7 工况3、4、5跟踪效果对比图

表2 DRAC鲁棒性实验仿真结果Table 2 Simulation results of robustness experiment of DRAC

图8 工况3、4、5控制力及防摆效果对比图

4 结语

本文针对存在参数不确定性和外部随机扰动的欠驱动双摆桥门式起重机防摇摆跟踪控制问题，提出了一种基于RBF神经网络的直接鲁棒自适应控制器；随后通过理论分析证明了目标控制律作用下系统的Lyapunov稳定性，并通过仿真实验验证了所提出控制器的控制性能。本文所提控制器的控制输入为小车实时位置与速度信息，起重机模型未知或不精确不影响其实现控制，控制器控制输出由RBF神经网络生成，整个控制器结构较为简单。由仿真结果可知，本文提出的轨迹跟踪控制器对目标轨迹的跟踪性良好，具体体现为位置跟踪误差小、吊钩与吊重残余摆动小；同时其鲁棒性较强，在起重机模型参数变化以及外部随机扰动影响下控制性能比较稳定。在后续工作中将安排实物实验以验证其实际控制性能。