缺资料地区降水系列的插补及验证

姬世保 杜军凯 仇亚琴 刘欢 吕向林

摘 要：针对部分地区降水资料缺乏的问题，以德清县为研究对象，提出了日尺度降水资料的插补方法，该方法通过对已有降水数据进行时间尺度转换和空间插值的方式插补出缺资料地区日降水数据。结果表明：①德清站插补结果中日降水强度、强降水量及连续有雨天数的误差均小于3%，与直接用周边站点的逐日数据对数据缺失站进行插值相比，各站月降水数据与实测值的相关系数平均提高0.11，均方根误差降低了42.3%;②将降水插补结果作为分布式水文模型的降水输入时，径流模拟效果得到了有效改善，1960—2018年模拟径流量和实测径流量系列的纳什效率系数由0.62提高到0.87，相对误差由-4.2%降至-2.3%;③日尺度降水插补结果的相关系数、5 d最大降水量及强降水量对研究区分布式水文模拟效果影响较大。

关键词：降水插补;缺资料地区;降水极端事件;交叉验证;WEP-L模型;分布式水文模型

中图分类号：TV214 文献标志码：A

doi：10.3969/j.issn.1000-1379.2021.05.008

Abstract： Aiming at areas which have no sufficient precipitation data， an interpolation method of daily scale precipitation data was proposed. This method could obtain the daily precipitation in some deficient data areas by means of conversion of time scale and space transplantation of existing data. The results show that a） the error between the simple daily intensity， very wet days and consecutive wet days of the interpolation result of Deqing Station and the measured series is less than 3%， compared with the daily data of interpolation result which gained by surrounding stations directly， the correlation coefficient between the monthly precipitation of each station and the measured value is increased by 0.11 on average， and the RMSE is reduced by 42.3%; b） when the interpolation results are used as the input in distributed hydrological simulation， the runoff simulation effect has been effectively improved， the Nash coefficient is increased from 0.62 to 0.87， and the relative error is reduced from -4.2% to -2.3% during the period of 1960-2018 and; c） the correlation coefficient， the 5-day maximum precipitation and very wet days of daily interpolation result have a great influence to the distributed hydrological simulation in the study area.

Key words： precipitation interpolation; data-deficient regions; precipitation extreme events; cross-validation; WEP-L model; distributed hydrological simulation

1 前 言

降水数据对水涵养评价、灾害风险管理、水循环模拟、植被分布和生态演变等研究具有重要價值[1-3]。现阶段，我国气象局管理的国家级气象站基本保持在相对稳定的2 200～2 400个[4-5]，平均密度为4 000～4 363 km2/站。胡庆芳[6]在赣江流域证实，当气象站网密度低于1 300 km2/站时，降水空间估计精度随站网密度变化而急剧变化，因此相对于全国来讲，测站不足、分布不均的问题仍然存在。另外，受自然条件及人为影响，水文站及雨量站停测、缺测、漏测现象时有发生[7]。已有资料时间序列的不一致性和不连续性给区域分布式水文模拟向精细化发展带来了诸多困难，通常情况下，站点数量越多、分布越合理、代表性越强，区域降水插值的不确定性就越小[8-9]。

为减小因停测、缺测、漏测所致的降水插值的不确定性，首先需要根据实际情况对缺失站降水进行插补展延，而后进行空间插值。目前，降水时间序列的插补方法主要有频率分析法[10]、水文相关法[11]、人工神经网络法[12]、贝叶斯线性回归法[13]、逐步回归法[14]等。现有研究在雨量站之间年、月尺度上的转换及空间插值取得了一系列丰硕的成果[15-18]，但分布式水文模拟、洪水预报等往往需要面尺度的日降水数据，而对于部分地区，个别气象站停测、缺测、漏测等现象导致一些不连续的降雨系列，如何充分利用仅存的降雨数据为水文模拟、洪水预报等提供服务，除借助遥感、雷达技术外，通过实测数据直接插补出面尺度日降水数据也是一个行之有效的办法，然而目前对这方面的研究较少。另外，插补结果是否能够捕捉降水极端事件、插补结果中的极端事件对降雨径流关系造成何种影响以及插补过程中需要注意哪些统计特征参数等方面的研究很少。

针对部分地区年、月尺度降水资料部分时段缺测及日降水数据严重缺乏的问题，笔者提出了缺资料地区面尺度日降水数据的插补方法。该方法充分利用现有不同时空尺度下的资料，集成点到点的插补展延与点到面的空间插值方法，并以此为基础插补出缺资料地区的面尺度日降水数据，最后以德清县为例，对上述方法进行多途径、多尺度的检验和应用。

2 数据来源及方法

2.1 数据来源

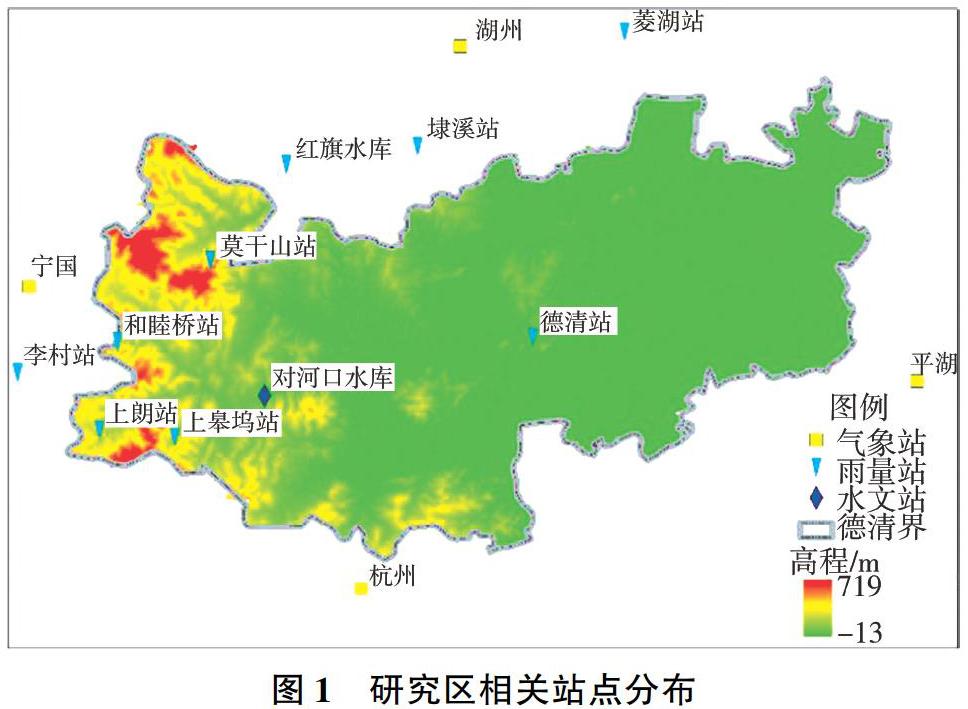
以德清县为研究区，该县位于浙江省湖州市，地处浙江省北部、杭嘉湖平原西部，位于浙江省八大水系之一的东苕溪中游。选取研究区附近9个雨量站，雨量站中仅位于东部平原河网区的德清站有日降水数据，其他站点仅有月降水数据，且存在不同程度的缺测、漏测现象，缺测站点占比达77.8%。另外选取水文站1个、气象站4个，在所有具有降水资料的站点中，有57.1%在研究区外，站点分布如图1所示。

降水资料一部分来源于国家气象局，另一部分来源于太湖流域水文年鉴，气象资料来源于国家气象局，水文资料来源于对河口水库管理局，各站数据资料详情见表1。

2.2 插补方法

首先，本着“资料质量较好、实测年限较长且面上分布均匀”的原则选取参证站，根据参证站的资料借助相关分析法插补出缺测站年降水数据。其次，将年降水数据分配到月，再将月尺度数据降尺度到日，最后通过改进的距离平方反比法（DRDS法）[19]进行空间插值。本文所提出的“面尺度日降水的插补方法”不同于传统分离式点与点间的插补展延和点与面之间的空间插值，其特点在于系统地进行降水“点—面”关系转化，最大限度地利用已有实测降水数据，插补方法具体步骤如下。

（1）对缺测站点年降水数据进行插补。找出满足条件的站点作为参证站，建立设计站和参证站年降水数据之间的相关关系，并根据相关关系插补出缺测年降水数据。

（2）年尺度到月尺度的转换。根据参证站年降水数据和月降水数据之间的关系，将设计站年降水数据分配到月。

（3）月尺度到日尺度的转换。选择距设计站最近且具有完整日尺度降水数据的站点作为参证站，按照参证站点降水月值和日值之间的关系，计算出设计站日降水量。

式中：Pr为参证站年降水量，mm;Pd为设计站年降水量，mm;γ为系数;c为常数;i为月份;αi为i月降水占全年的比例;Pdi为设计站i月降水量，mm;Pri为参证站i月降水量，mm;Pjd为设计站第j天降水量，mm;Pjr为参证站第j天降水量，mm;βj为第j天降水占当月的比例;j为逐月第j天;s为逐月最后一天。

整个降水系列的插补及验证过程如图2所示。

2.3 插补结果检验方法

对插补结果进行多途径、多尺度的检验，检验的方式有直接检验和间接检验两种，检验的指标有相关系数、均方根误差、平均相对偏差、纳什效率系数、相对误差，检验的内容有极端降水指标、降水日值、降水月值以及降水径流模拟效果。

对有实测日降水数据的站点采用直接检验法，即直接比较插补结果的特征值及降水过程和实测系列的差异。日尺度插补结果的检验，主要检验极端降水指标。世界气象组织（WMO）在1998—2001年气候变化监测会议上提出代表气候变化的一套极端气候指数，其中有27个指数作为核心指数被广泛使用，包含16个极端温度指标和11个极端降水指标[20]。综合考虑指标重复性和各指标在研究区的适用性，选取其中6个极端降水指标（见表2）代表研究区内极端降水情况。日降水强度代表测站控制区内降水的总体水平，5 d最大降水量代表连续5 d内的最大降水水平，年降水总量代表控制区内降水的总体水平，强降水量代表降水极端程度，连续无雨天数代表测站控制区干旱水平，连续有雨天数代表控制区湿润水平。

对有实测月尺度降水数据的站点，只检验其月尺度降水数据，采用交叉验证法[21]进行检验。交叉验证是依次减少一个样本点，然后使用其余的样本进行建模，再通过模型估算该样本点的相关结果，最后计算模型估算结果相对于实测值的误差。本文选择相关系数（ρXY）、均方根误差（RMSE）及平均相对偏差（ARE）3项指标综合判断插补结果的合理性，其中相关系数、均方根误差和平均相对偏差的计算方法如下：

式中：X为实测系列值;Y为插补系列值;Cov（X，Y）为X、Y系列的協方差;D（X）、D（Y）分别为X系列与Y系列的方差;N为实测站点个数;Pauti为第i个站点的实测降水量;Paut-为所有实测站点的平均降水量;Ci︿为第i个站点的插值结果;ρXY、RMSEj、AREj分别为第j次验证的相关系数、均方根误差和平均相对偏差。

对于无实测日降水数据但是有实测径流数据的站点，可通过间接的方法检验降水插补结果的合理性。间接方法是以水文模型为载体，通过水文模拟效果间接地判断降水插补结果的合理性，模拟效果的好坏由相对误差和纳什效率系数来判断。

3 插补结果检验

3.1 直接检验

3.1.1 日尺度插补结果检验

研究区有5个站点有逐日实测降水数据，其中4个在研究区外，仅作为插补的参证站，不做进一步验证，只针对研究区内有逐日资料的德清站进行日尺度插补结果的检验。检验之前首先利用除德清站外其他站的资料插补出德清站所在位置的逐日降水数据，然后和实测值进行对比验证。为检验插补方法的实用性，设计了两套插补方案。方案A：直接用周边有逐日降水数据的站点对数据缺失站进行插值，插值方法统一采用DRDS法;方案B：借助上文提出的“面尺度日降水的插补方法”插补出缺失站降水数据。最后使用Rclimdex软件计算德清站不同方案下插补结果的多年平均年降水量、日降水强度、5 d最大降水量、强降水量、连续无雨天数和连续有雨天数6个指标，不同插补方案下极端降水指标多年平均值见表3。

从表3可以看出，两套方案插补结果相差较大的极端降水指标有强降水量及连续有雨天数，方案A强降水量与连续有雨天数的误差分边是方案B的3.4倍与59.2倍。方案B中，6个极端降水指标中插补误差绝对值最大的是5 d最大降水量，为-12.24%，其余指标误差都在10%以内，其中，日降水强度、强降水量及连续有雨天数的插补误差都不到3%。和实测系列相比，方案B插补结果偏大的有日降水强度、年降水量、强降水量及连续有雨天数，偏小的有5 d最大降水量和连续无雨天数，反映出极端降水事件较强的两个指标分别是5 d最大降水量和強降水量，两者一个偏小，一个偏大。

方案B误差较小的原因：首先是其充分发挥了研究区内所有的实测降水数据;其次是所用空间插值方法不仅考虑了插值距离，同时还考虑了参证站与插补站之间的相关性。方案B在降低降水资料点到点的插补展延误差的同时还考虑了降水的空间变异性，与方案A相比略有优势，但与实测值相比仍存在误差。究其原因，可能有以下几点：①插补用的是改进的距离平方反比法，该方法和其他空间插值方法相比，虽然考虑了降水的空间变异性，但仍会有一定的误差;②插补结果是控制站点所在子流域的面降水量，而实测数据是控制站点的点降水量，另外，子流域划分本身就有一定的不确定性，它和水系提取的精度及汇流累计数的大小等都有关系，因此用点的数据检验面的数据也会造成一定的误差。

3.1.2 月尺度插补结果检验

所选站点中共有9个站点有月尺度降水数据，分别是菱湖站、对河口水库站、红旗水库站、和睦桥站、李村站、莫干山站、上皋坞站、上朗站、埭溪站，对于此类站点，只能检验其月尺度插补结果的合理性，检验的具体过程如下：①选取14个具有降水资料的站点作为样本点;②选择需要检验的站点，然后用余下的13个站点建立日降水估算模型，得到面尺度日降水数据;③提取出检验站所在位置逐月降水数据并和该站实测值进行比较。

累计交叉验证9次，得到各站插补结果和实测值的平均相关系数为0.94、均方根误差为30.3 mm、平均相对偏差为87.9%。为更直观、全面地反映上述9个站点的插补效果，引入泰勒图[21]，图3为9个插补站验证结果的泰勒图。

由图3可见：各站相关系数介于0.84～0.99，均值为0.94;平均相对偏差介于83.2%～92.8%，均值为87.9%;均方根误差介于14.9～51.4 mm，均值为30.3 mm。

从图3可以看出上朗站交叉验证结果距真值点（德清站）最近，可见该站插补效果最好。上郎站所在位置海拔较低，受地形地貌等其他因素的影响相对较小，该站周围站点密集，插值距离较近，这些因素都有利于该站降水的插补。

为了进一步检验插补结果的实用性，分别计算了方案A、B插补结果与实测系列在月尺度上的相关系数、均方根误差及平均相对偏差，见表4。

由表4可见，就相关系数而言，方案B较方案A平均提高0.11，提高比例达13.3%，提高最显著的是红旗水库站，达19.5%，最差的是对河口水库站和德清站，仅为1.2%。从图1可以看出大部分测站位于西部山区，而平原区仅有德清站一个，因此，德清站插补效果差的原因可能是其周围站点稀少;就均方根误差来看，10个站点的平均均方根误差由方案A的52.5 mm减小到方案B的30.3 mm，降低了42.3%，极大地降低了月降水的插补误差;而和相关系数和均方根误差相比，方案B平均相对偏差仅降低1.4，差异相对较小。

3.2 间接检验

为了对插补结果进行多方验证，将A、B两方案插补结果应用于有径流资料的对河口水库站控制区分布式水文模拟，并选用WEP-L模型[22]进行模拟，该模型是一款以“子流域套等高带”为基本计算单元的流域分布式水文模型，模拟过程中需要参与率定的高敏感参数有分区临界暴雨量、气孔阻抗、土壤厚度、洼地储流深、土壤饱和导水系数、河床渗透系数、含水层厚度以及坡面和河道的曼宁系数。

拟定模型率定期为1960—2000年，验证期为2001—2018年，不同时间段降水径流模拟计算结果见表5，不同方案径流模拟过程对比如图4和图5所示。

和方案A模拟结果相比，方案B纳什效率系数由0.62提高到0.87，相对误差由-4.2%降到-2.3%。究其原因，就插补结果多年月平均特征值来说，方案B多年月平均降水量为134.33 mm，方案A为134.31 mm，二者仅差0.02 mm，而在天然状况下降水和径流呈正相关，因此两种方案下径流模拟结果相对误差的差异较小;方案B全系列降水的相关系数为0.94，方案A为0.83，由于方案B降水插补结果与实测系列相关性更好，更能体现出降水的动态变化，因此其径流模拟结果的动态变化也更加接近实测系列。此外，从德清站日降水的验证结果中可以看出方案B插补结果能够很好地捕捉到连续有雨天数、日降水强度及强降水量，这些指标对产流有着重要影响，尤其是雨强，因此方案B下分布式水文模拟效果较好的原因亦可能是其对雨强信息的捕捉能力更好。

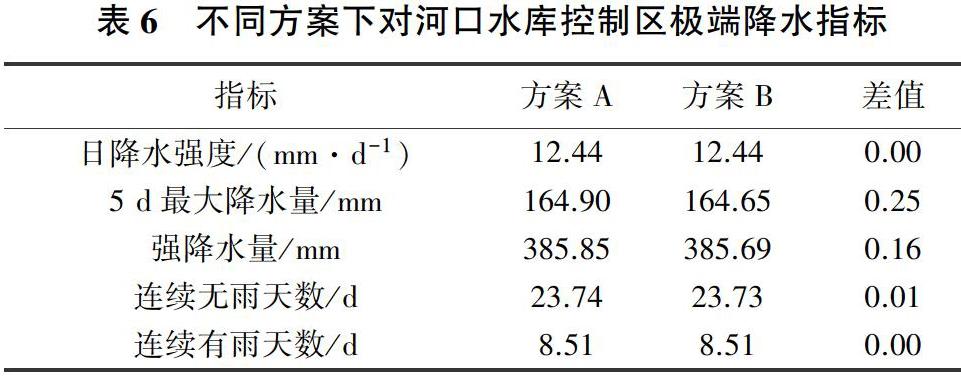
对比分析不同方案插补结果的极端降水指标（见表6），5项指标中差别较大的是5 d最大降水量和强降水量，就径流模拟结果来看，将方案B插补结果作为模型的降水输入时，径流模拟效果更优，间接说明方案B对极端降水事件把握得更为准确。由于两种方案的极端降水指标中只有5 d最大降水量和强降水量差异明显，而方案B降水径流模拟结果又明显优于方案A，因此一定程度上可以说所选的极端降水指标中5 d最大降水量和强降水量对径流模拟效果影响较大。

为探究插补方法在不同时段的效果，分别分析了对河口水文站控制区1970—1980年及2010—2018年两个时段在不同降水输入（方案A、B降水插补结果）情况下的降水径流模拟结果（见表7）。模拟结果显示：1970—1980年，方案B较方案A的纳什效率系数提高76.0%、相对误差降低38.8%;2010—2018年，方案B较方案A纳什效率系数提高38.5%、相对误差降低27.7%。

4 结 语

借助14个水文气象站不同时空尺度的数据，利用“面尺度日降水的插补方法”对研究区逐日降水数据进行了插补，并对插补结果进行了多途径、多尺度的验证，最终得到以下结论。

（1）与直接用有逐日数据的站点对数据缺失站进行插值相比，利用本文提出的面尺度日降水的插补方法对缺测站点降水数据进行处理后，有效降低了研究区日尺度降水数据的插补误差，使得各站平均相关系数提高了0.11，平均均方根误差降低了42.3%。

（2）插补误差最大的极端降水指标是5 d最大降水量，达-12.24%，其余指标误差都在10%以内，插补结果偏大的有日降水强度、年降水总量、强降水量及连续有雨天数，偏小的有5 d最大降水量和连续无雨天数。

（3）將插补后的降水作为分布式水文模拟的输入值时，近60 a径流模拟效果得到了有效改善，对河口水库站纳什效率系数由0.62提高到0.87，相对误差由-4.2%降到-2.3%。

（4）在分布式水文模拟过程中发现，日尺度降水系列的相关系数、5 d最大降水量以及强降水量对径流模拟影响较大。

参考文献：

[1] 吴昌广，林德生，周志翔，等.三峡库区降水量的空间插值方法及时空分布[J].长江流域资源与环境，2010，19（7）：52-58.

[2] TEEGAVARAPU R S V， MESKELE T， PATHAK C S. Geo-Spatial Grid-Based Transformations of Precipitation Estimates Using Spatial Interpolation Methods[J]. Computers & Geosciences， 2012，40（3）：28-39.

[3] 赵林，武建军，吕爱锋，等.京津风沙源区植被变化对降水的响应规律研究[J].北京师范大学学报（自然科学版），2010，46（5）：610-618.

[4] SHEN Y， XIONG A Y. Validation and Comparison of a New Gauge-Based Precipitation Analysis over Mainland China[J]. International Journal of Climatology， 2016， 36（1）： 252-265.

[5] 王丹，王爱慧.1901—2013年GPCC和CRU降水资料在中国大陆的适用性评估[J].气候与环境研究，2017，22（4）：446-462.

[6] 胡庆芳.基于多源信息的降水空间估计及其水文应用研究[D].北京：清华大学，2013：118-119.

[7] 郭彦，林秀芝，侯素珍，等.基于EMD和BP算法的降水数据插补[J].水资源与水工程学报，2015，26（2）：16-21.

[8] GIRONS L M， WENNERSTOM H， NORDéN L A， et al. Location and Density of Rain Gauges for the Estimation of Spatial Varying Precipitation[J].Geografiska Annaler： Series A， Physical Geography， 2015， 97-103.

[9] 李妮娜，李建.中国西南复杂地形区降水观测年际变化代表性问题初步分析[J].高原气象，2017，36（1）：119-128.

[10] 高文义，郭海华.用频率分析方法对年降水量系列插补延长的探讨[J].吉林水利，2008（3）：3-4.

[11] TEEGAVARAPU R S V， RAMESH S V. Estimation of Missing Precipitation Records Integrating Surface Interpolation Techniques and Spatio-Temporal Association Rules[J]. Journal of Hydroinformatics， 2009， 11（2）： 133.

[12] 田琳，王龙，余航，等.基于BP神经网络的缺测降水数据插补[J].云南农业大学学报（自然科学），2012，27（2）：281-284.

[13] 刘田，阳坤，秦军，等.青藏高原中、东部气象站降水资料时间序列的构建与应用[J].高原气象，2018，37（6）：1449-1457.

[14] 陈福容，任立良，杨邦，等.基于逐步回归分析的雨量信息插补计算和应用[J].水电能源科学，2009，27（2）：7-10.

[15] TEEGAVARAPU R S V. Use of Universal Function Approximation in Variance-Dependent Surface Interpolation Method： an Application in Hydrology[J]. Journal of Hydrology， 2007， 332（1）： 16-29.

[16] Eischeid J K， Pasteris P A. Creating a Serially Complete， National Daily Time Series of Temperature and Precipitation for the Western United States[J]. Journal of Applied Meteorology， 2000， 39（9）： 1580-1591.

[17] SHEN S S P， DZIKOWSKI P， LI G， et al. Interpolation of 1961-97 Daily Temperature and Precipitation Data onto Alberta Polygons of Ecodistrict and Soil Landscapes of Canada[J]. Journal of Applied Meteorology， 2001， 40（12）： 2162-2177.

[18] 王志良，黄珊，陈海涛.黄河流域水文数据插补方法比较及应用[J].人民黄河，2020，42（7）：14-18.

[19] 王喜峰，周祖昊，贾仰文，等.几何插值法在大尺度长系列降雨插值中的比较和改进[J].水电能源科学，2010，28（12）：1-3.

[20] TSAI C H， KOLIBAL J， LI M. The Golden Section Search Algorithm for Finding a Good Shape Parameter for Meshless Collocation Methods[J].Engineering Analysis with Boundary Elements， 2010， 34（8）： 738-746.

[21] TAYLOR K E. Summarizing Multiple Aspects of Model Performance in a Single Diagram[J]. Journal of Geophysical Research， 2001， 106（D7）： 7183.

[22] 贾仰文，王浩，倪广恒，等.分布式流域水文模型原理与实践[M].北京：中国水利水电出版社，2005：113.

【责任编辑 张 帅】