折叠链条下落过程的动力学分析*

张丽颖，林金妮，吴臆洋，邱为钢

(湖州师范学院理学院,浙江 湖州 313000)

1 引言

链条下落问题是中学物理奥赛的一种常见题目，文献[1]中的第28 题“百变柔软绳”，和文献[2]中的例题4-6，都提到了同一模型：一个质量均匀分布的绳子(链条)，折成两半，尽量靠近,称为折叠链。折叠链左半部分的上端固定，右半部分的上端（称为自由端）静止释放。那么，这个自由端是如何下落的？文献[1]和[2]都假设自由端是做自由落体运动，基于这种前提，计算得到了折叠链下落过程中固定端受到的拉力。这样的假设对吗？

检验一个物理假设是否正确最便利的方法是做实验。通过简单的对比实验，将U 形链右端和一个小钢球，在同一高度上同时释放。拍摄下落视频，比照两者下落到最低点所需的时间。多次实验表明：折叠链自由端下落，比自由落体运动更快。文献[2]的作者考虑到该问题后，在书的第二版（文献[3]）中对折叠链下落模型进行修改，在折叠链右端固定（系）一个小球（重物），假设体系在下落过程中机械能不变，由此可得到小球的运动方程。在理论方面，已有研究表明当把链条（绳子）离散化，即看作是N 个通过光滑的铰链链接且质量均匀分布的杆时，可直接得出N 个杆的运动方程（质心和转动）并进行数值求解。当杆数目N 取40 时，理论数值计算也发现折叠链的自由端比自由落体下落的快。实验和（离散化后的）模拟都表明，折叠链的自由端下落不是自由落体运动。

在此基础上，本文将从理论和实验两方面对折叠链下落运动进一步展开探究。在假设折叠链下落机械能不变的前提下，建立动力学模型得出链条自由端的运动方程。将理论与实验结果进行分析对比，研究不同初始情况下折叠链自由端下落距离随时间的变化关系。

2 理论推导

设折叠链整个长度为L、质量为M，其中链条(a)部分下落,(b)部分静止不动，中间链接部分忽略不计，如图1 所示：

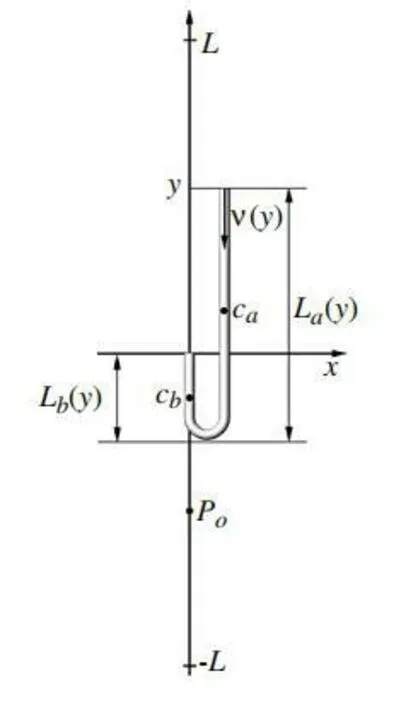
图1 折叠链下落示意图

以左端固定端为原点，设自由端的坐标是y，左右两端链条的长度分别为Lb和La，质心分别为Ca和Cb，其中Po为链条静止下垂时的质心位置。

由图可知：

同时总的链条长度不变，则

由此计算得到

链条左右两端的质量为

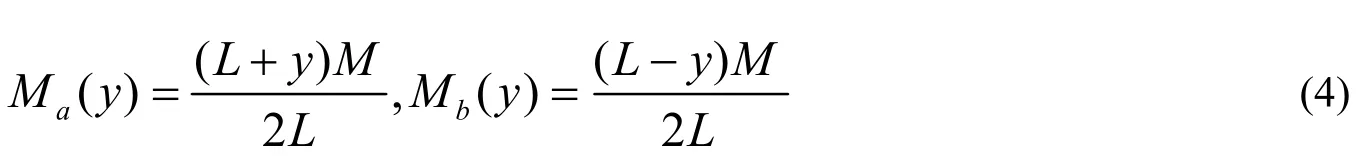
可得左右两段链条质心的坐标为

为方便计算，势能零点取为整个链条完全静止下垂时候的质心坐标ypo= -L/2处。由此得到左右两段链条的重力势能Ua(y)和Ub(y)为

设起始时刻链的自由端位于yo处，此时链的总势能为

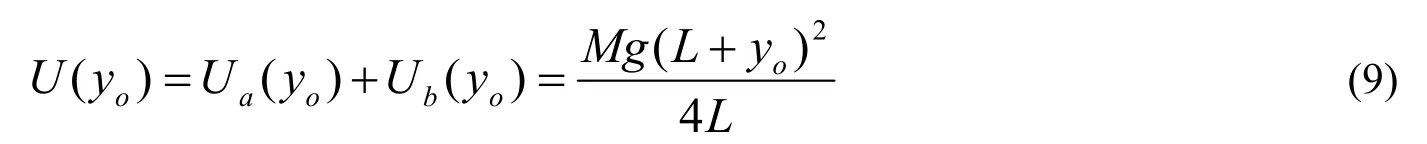
假设链条右边下落部分，整体以自由端的速度v(y)一起下落，那么这部分的动能为

假设落链的机械能不变，得到

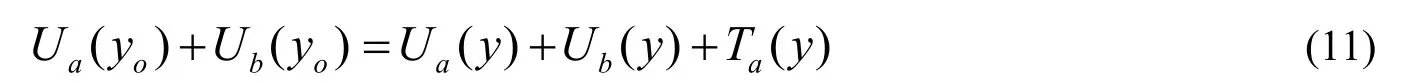
把公式(10)代入(11)式中，计算得到折叠链自由端的下落速度大小为

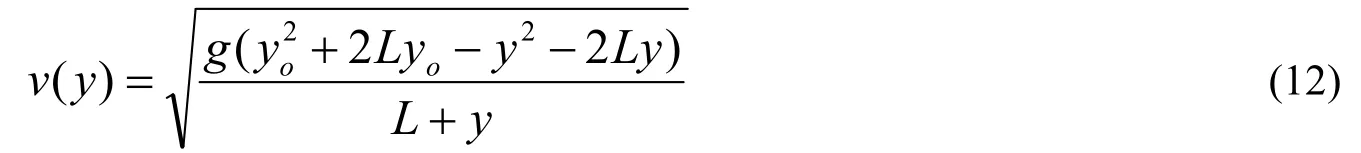
在下落过程结束快结束时,(13)式右边根号下分母L+y趋向与零，速度发散。说明这个模型在下落末端失效。从(12)式中可以得到理论下落时间：

这个时间是有限的，不会发散。

3 实验对比

3.1 实验模拟

取一段大约长为一米的链条，用钉子将其中一端固定在泡沫塑料板上进行实验。为了便于测量、对比读出实际距离值，板上贴有长度标度的白纸。从固定端到自由端的长度L= 85.2厘米。起始时，自由端可以高于、等于或者低于固定端，如图2 所示:

图2 固定端和自由端不同高度下的释放时刻

对于同一高度，实验使用帧率为240fps 的高速摄像；对于不同高度，使用帧率为120fps 的高速摄像。fps的意思是frame per second，即1 秒钟能拍摄多少张（帧）画面,所以相邻图片的时间间隔为帧率的倒数分之一秒。用视频软件KMPPlayer，逐帧提取图片。对于同一高度帧率为240fps 的视频，每隔2 幅图片进行测量，得出距离数据的时间间隔为 Δt= 3/240= 0.0125秒。对于不同高度，每幅图片都测量，得出距离数据时间间隔为 Δt= 1/120秒。

3.2 拟合对比分析

针对三种折叠链条下落情况，根据式(12)理论模拟出不同情况下链条自由端下落位移和时间的图像关系后，通过实验测量出链条下落时图片中链条自由端的位移，并将测量点绘制于y-t 图像当中。利用Mathematica软件将理论图像和实验结果相拟合，以便于更加直观、清晰的对比理论值与实际值并加以分析。

对于同一高度，(12)式中的yo=0，理论下落时间是0.353 秒。数值求解(12)式，得到的自由端下落曲线（实线），与实验数据（三角形符号）和自由落体运动（虚线）对比如图3 所示：

图3 起始自由端与固定端同一高度时的y-t 图

对于高于固定端10 厘米，(12)式中的yo= 0.1，理论下落时间是0.373 秒。数值求解(12)式，得到的自由端下落曲线（实线），与实验数据（三角形符号）和自由落体运动（虚线）对比如图4 所示：

图4 起始自由端高于固定端时的y-t 图

对于低于固定端10 厘米，(12)式中的yo=-0 .1，理论下落时间是0.332 秒。数值求解(12)式，得到的自由端下落曲线（实线），与实验数据（三角形符号）和自由落体运动（虚线）对比如图5 所示：

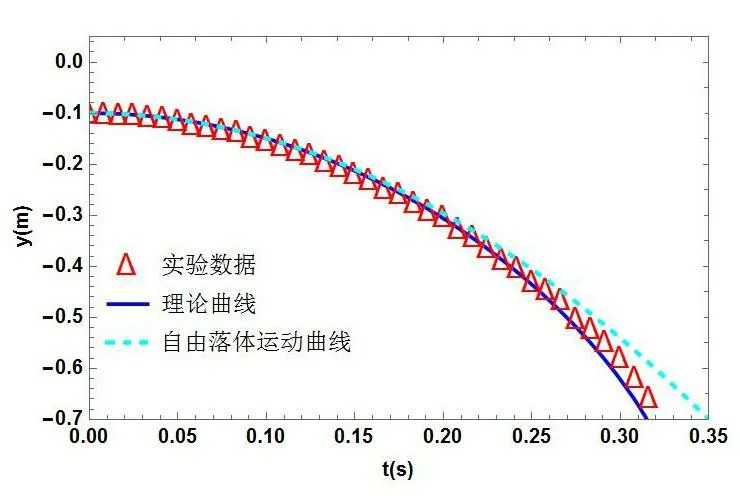
图5 起始自由端低于固定端时的y-t 图

通过对比图3、4、5 可以看出，在理论下落时间的百分之八十之内，实验数据基本落在理论曲线上。在理论下落时间百分之六十之内，实验数据、理论曲线和自由落体曲线，三者基本吻合。这说明下落早期，自由端可以近似看作自由落体，但不是严格理论意义上的自由落体。区别最大的是下落过程的末期，无论实验还是数值模拟显示，最下面部分的链条不再是直线形，而是折线形，存在水平方向的运动。理论模型(12)式中，没有考虑到这部分的横向动能，所以会出现末期下落速度发散的情形。

4 结论

假设下落过程中链条还是折叠的，即两段线段的联合体，左段静止，右段整体下落，且机械能守恒（不变），由此得到了右段最上端（自由端）的下落方程。这个运动方程并不是自由落体运动方程。三种实验数据基本和理论曲线重合，但这也并不能说明链条下落过程中机械能严格守恒，这有可能是凑巧，也可能有更深刻的机理，正如文献[4]中所探讨的，有待进一步展开研究。