基于残差网络特征融合的高光谱图像分类
韩彦岭,崔鹏霞,杨树瑚,刘业锟,王静,张云
(上海海洋大学信息学院,上海 201306)
0 引言
高光谱图像是若干个光谱波段组成的三维立体图,含有丰富的空间信息和光谱信息,并且具有较高的空谱分辨率,能提取到不同地物的细节特征,在农作物监测、海洋环境监测、地图绘制等方面发挥着重要作用[1],因此利用高光谱图像进行地物分类识别已经成为国内外研究热点。近年来很多分类方法被应用于高光谱图像分类中,包括支持向量机(support vector machine,SVM)[2]分类法、决策树分类法、最大似然分类法等,但是这些传统分类方法由于只能提取到高光谱图像的浅层特征信息而忽略了深层特征信息导致其分类精度的进一步提高受到限制,另外,高光谱图像数据量巨大,且存在较多冗余信息,也给传统分类方法的处理提出了挑战。
由于深度学习方法可以较好地提取图像的深层特征信息,近年来逐渐受到重视并广泛应用于高光谱图像分类领域,常用的网络模型有卷积神经网络(convolutional neural networks,CNN)、深度置信网络(deep belief nets,DBN)、循环神经网络(recurrent neural network,RNN)等,比如文献[3]将传统的深度CNN进行改进,采用分层特征融合的方法,得到更加有效的深度特征;文献[4]基于反卷积提取高光谱图像的高层特征,提出了一种结合高层特征空间和迁移学习网络的遥感地物图像分类算法,有效提高了分类精度;文献[5]基于由光谱特征和纹理特征作为浅层特征,尺度不变特征变换(scale-invariant feature transform,SIFT)经编码后得到的中层特征,以及CNN提取的深层特征,基于不同层次特征选用不同的分类器进行分类。研究表明利用深度学习一定程度上可以有效获得深层特征信息,但是还不能充分融合深度学习网络中各个层之间的深层特征,需要结合其他算法使层与层之间的深层特征得以充分利用。另外,在像素级分类中,高光谱遥感图像的训练样本输入尺寸偏小,深度学习模型的层数受到限制,模型优化的可能性较少,一定程度上也限制了高光谱图像分类精度的提高。2015年He等[6]提出深度残差网络,在ImageNet大规模视觉识别竞赛中获得了图像分类和物体识别的优胜,解决了网络层数不足的问题;文献[7]提出一种基于深度残差CNN的高光谱遥感数据的方法,提高分类的准确度;文献[8]利用CNN提取到空间光谱特征的同时,结合了三层残差网络模块提高了高光谱图像的分类精度。
基于以上研究,针对高光谱图像分类中目前存在的样本输入小,网络层数有限,导致深层特征无法充分提取的问题,本文提出一种基于残差网络特征融合的高光谱图像分类方法。利用残差网络加深网络层数,解决了高光谱图像分类中由于训练样本输入尺寸偏小导致的网络层数受限问题;另外,通过反卷积算法实现特征图的扩充并进行不同尺度特征的深度融合,充分挖掘高光谱图像中的深度特征信息,进一步提升高光谱图像分类精度。在“珠海一号”卫星拍摄的江苏太湖和安徽巢湖两个区域数据上进行分类实验,以验证本文方法的有效性。
1 基于残差网络特征融合的高光谱图像分类方法
本文方法主要思想是利用残差网络加深网络层数,通过反卷积扩大特征图,并将不同尺度的特征进行特征融合,进一步挖掘高光谱图像中的深层特征,以此获得较高的分类精度。本文首先对高光谱图像的原始数据进行主成分分析(principal component analysis,PCA),利用PCA将图像的重要特征集中在第一个波段中,处理成二维图像作为样本输入;考虑到深度学习网络层数加深会造成梯度消失,以及网络层数加深会造成参数过大的问题,利用残差网络中的恒等映射减少训练过程中的参数,并且缓解了梯度消失的问题;传统的残差网络只能够一层一层提取特征并输入到下一层残差单元,层与层之间的特征没有被充分地挖掘和利用,限制了高光谱图像分类精度的进一步提升,因此本文利用反卷积扩大特征图,并且通过多尺度融合算法使不同层的特征进行融合,充分挖掘高光谱图像中的深层特征信息以提高分类精度。本文总体架构如图1所示,主要包含3部分,第一部分为数据预处理,第二部分为算法实现部分,包含本文算法以及与其他方法的对比,第三部分为精度验证,通过计算混淆矩阵,得出总体分类精度(overall accuracy,OA)和Kappa系数验证精度的一致性。

图1 本文总体框架Fig.1 Overall framework of this paper
1.1 改进的残差网络
残差网络的恒等映射的设计,使误差不会继续增加,因为可以从x恒等映射到F(x),这就是残差网络解决深度学习中因网络层数增加而导致梯度消失问题的关键所在。如图2所示,把输入x传到输出作为初始结果,输出结果为Y=F(x)+x,当F(x)=0时,Y=x,也就是恒等映射。于是,残差网络相当于将学习目标改变了,不再是学习一个完整的输出,而是目标值Y和x的差值,也就是所谓的残差F(x)=Y-x,因此,后面的训练目标就是要将残差结果逼近于0,随着网络加深,准确率不下降。

图2 残差网络构思图Fig.2 Conceptual diagram of the residual network
图3为本文改进的残差网络结构,convij称为残差层,其中i表示第i个残差层,j表示对应残差层中的残差单元,如conv1j为第一残差层,conv2j为第二残差层,虚线框中称为残差块,包含6个残差单元和2个池化层,每个残差单元的卷积核大小均为3×3,32和64为卷积核个数。网络中卷积核大小一般为3×3,5×5,7×7,考虑本文中样本输入大小为27×27,若选用5×5和7×7大小的卷积核,会导致网络模型层数较少,优化网络模型的可能情况更少,因此本文中选取卷积核大小为3×3。该网络结构先经过3个残差单元和1个池化层,将池化后的输出作为反卷积Dconv1的输入,反卷积中卷积核大小为5×5,卷积核个数为64,步长为1,无填充层,激活函数为ReLU。随后将第一个池化层的输出作为第二个残差层的输入,经过三个残差单元和一个池化后的输出作为反卷积Dconv2的输入,Dconv2中除了卷积核大小为3×3与Dconv1中不同外,其余参数设置均一样。Dconv1和Dconv2输出维度不同的特征进行多尺度融合(M1),将低层特征扩大融合为同维度的特征后输入到残差块中进行特征提取,其中残差块与第一残差层和第二残差层参数设置完全一样,分别命名为第三残差层和第四残差层,最后通过conv5残差层,增加了特征的数量,最后将提取到的特征输入到全连接层FC和softmax分类器进行分类。

图3 改进的残差网络结构Fig.3 Improved residual network structure
1.2 卷积和反卷积

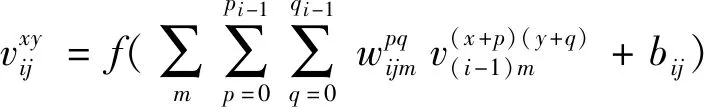
(1)
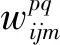
本文采用ReLU函数作为激活函数,该函数不存在梯度消失问题,使得模型的收敛速度维持在一个稳定的状态,其公式为:
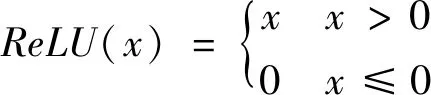
(2)
卷积层的主要作用是提取特征信息,反卷积为卷积的逆运算,反卷积的主要作用是通过信息填充使特征图扩大。在本文算法中,由于不同层的特征图维度不同,不能直接进行融合,需要将高层特征图扩大。卷积和反卷积示意图如图4所示。图4中蓝色为卷积输入的特征图,绿色为卷积(反卷积)之后的特征图,图4(a)为卷积过程,卷积核大小为3×3,步长为1×1,无填充层,将图中大小为4×4的特征图卷积为2×2。图4(b)为反卷积过程,卷积核大小为3×3,步长为1,填充2层(虚线部分为填充层),将图中大小为2×2的特征图反卷积为4×4。在步长为1时,反卷积输出特征的计算公式为:
out=n+2s-d+1,
(3)
式中:out为输出特征图大小;n为输入特征图大小;s为填充层数;d为卷积核个数。
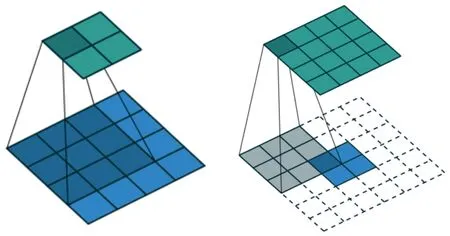
(a)卷积过程 (b)反卷积过程
1.3 多尺度融合
在卷积网络进行特征提取的过程中,随着网络层数的加深,每层获得的特征信息会有所不同,低层网络侧重提取地物颜色、边缘等纹理特征信息,高层网络侧重提取高层抽象特征,同时获得的特征图维度也会逐渐缩小,由于不同层的特征信息具有不同的特点,只利用最后的高层信息进行地物分类会在一定程度上丢失部分信息。因此通过多尺度特征融合可以将低层网络的特征图和高层网络的特征图进行融合,通过特征融合获取更多来自不同卷积层的空谱特征,从而进一步提升高光谱图像的分类精度。本文多尺度融合思想[10]源于RefineNet网络中的多分辨率融合(multi-resolution fusion,MRF)模块,经过残差块后将提取到的不同尺度的特征图实现融合,不同尺度的特征融合过程示意如图5所示,对18×18,9×9和3×3的特征图分别进行二维卷积(其中,padding层为same、卷积核大小为3×3),再进行不同Scale的上采样过程(Scale为扩大整数倍),其中9×9特征图扩大2倍变为18×18,3×3的特征图扩大6倍变为18×18,最后将所有的18×18的特征图加和后输入到下一层。
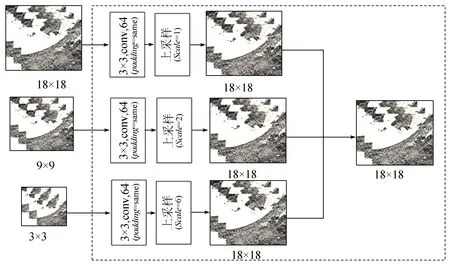
图5 多尺度融合结构图Fig.5 Multi-scale fusion structure diagram
1.4 算法描述
基于以上算法分析,本文的算法实现过程描述如下:
开始:
输入:原始高光谱图像
1)样本标签。
①对原始高光谱图像做样本标签,形成样本库;
②按一定比例将样本库分为训练样本和测试样本;
2)提取空间特征。
③通过PCA算法求得原始图像的第一主成分作为输入;
3)改进残差网络。
a.训练阶段:
④从训练样本中按照迭代批次(batch)随机输入到第一残差层中,进行卷积核大小为l×l的最大池化;
⑤将步骤④中的输出作为第二残差层的输入,再进行卷积核大小为l×l的最大池化;
⑥将步骤④,⑤中的输出作为反卷积的输入,卷积核大小为ci×ci(表示第i层卷积核大小为c),步长为1;
⑦将两个反卷积之后图像进行多尺度特征融合;
⑧将⑦中的输出作为第三残差层的输入,然后进行卷积核大小为l×l的最大池化;
⑨将步骤⑧中的输出作为第四残差层的输入,再进行卷积核大小为l×l的最大池化;
⑩将步骤⑨中的输出作为conv5残差层的输入,获得更多的特征;



b.测试阶段:


输出:混淆矩阵,OA,Kappa系数。
结束
2 实验结果与分析
2.1 数据描述
本文采用的数据集为珠海一号卫星高光谱数据,该数据共有32个波段,空间分辨率是10 m,原始图像大小为5 056×5 056。分别在江苏省无锡市太湖地区和安徽省合肥市巢湖地区裁剪2个3 000×3 000的实验区域,其中太湖地区影像成像时间为2018年10月1日,左上角经度为E120°11′34″,纬度为N31°06′52″,文中称为太湖,如图6(a);巢湖区域影像成像时间为2019年4月17日,左上角经度为E117°14′41″,纬度为N31°50′25″,文中称为巢湖,如图6(b)。

(a)太湖及局部放大图像 (b)巢湖及局部放大图像
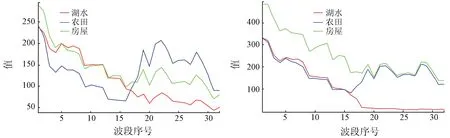
实验中将数据分为湖水、房屋、农田3类,依据光谱曲线和谷歌地图两者结合一起以像素点为单位做样本标签,太湖和巢湖的平均光谱曲线如图7所示,红色表示湖水,绿色表示房屋,蓝色表示农田,从这2个图中可以看出数据中3种类别地物可以较好地区分。太湖实验数据中带标签的像素共有29 346个,巢湖带标签的像素共有29 512个,实验中训练样本与测试样本都是按照1∶1的比例,具体数量见表1。
(a)太湖区域 (b)巢湖区域
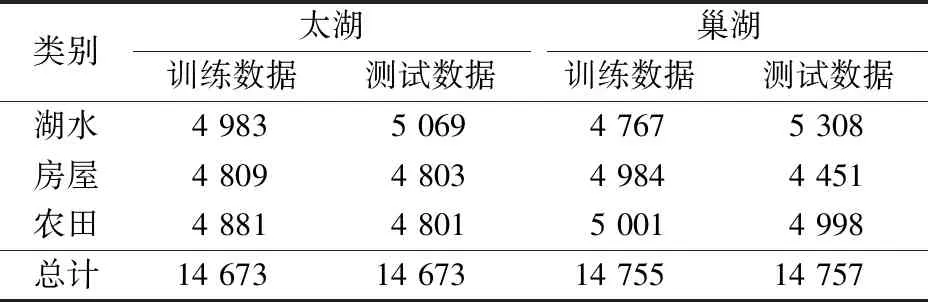
表1 数据集样本个数Tab.1 Number of data set samples (个)
2.2 预处理与实验设置
预处理方式采用PCA算法对高光谱图像降维,将32个波段的数据降维为1个波段作为输入,其中对于训练样本是随机输入,测试样本为总样本数减训练样本,训练样本的随机性使模型精度不完全一致,因此每个实验都是训练5次确保实验结果的稳定性,使实验结果更加具有说服力。
深度学习中包含大量待训练参数,网络结构直接影响训练参数的多少,结构越复杂训练参数越多,训练难度也会增加,固定部分参数是非常有必要的。本文实验中设置学习率为0.000 5,丢弃比例(drop_prob)为0.5,批量处理(batch_size)大小为20,迭代次数为20 000次。改进残差网络参数及其网络设置见表2,同样的两套数据进行孪生网络[11],SVM[12],CNN[13],GLCMCNN[14]和传统残差网络的对比实验。孪生网络(Siamese)是将两个输入映射到统一特征空间中,并共享权值,判别两个样本是否为正样本或者负样本,只需一次前向传播操作就可以计算出精度;SVM采用径向基函数作为核函数,参数g和惩罚因子c都是经过5次交叉验证寻优得到;CNN参数设置见表3;GLCMCNN中选取了平均值、方差、熵、偏度4个值,再结合CNN网络进行分类,其中CNN网络参数与表3相同;传统残差网络参数及其网络设置见表4。

表2 改进残差网络Tab.2 Improved residual network

表3 CNN网络结构Tab.3 CNN network structure

表4 传统残差网络Tab.4 Traditional residual network
2.3 实验结果与分析
表5为本文方法与孪生网络,SVM,CNN,GLCMCNN和传统残差网络在太湖和巢湖数据集进行对比的分类结果,从总体分类精度和Kappa系数看,本文方法获得了最高的分类精度,证明该算法分类性能较好,总体分类精度和Kappa系数的值均为“平均值±标准差”格式。表5中,相对传统方法,本文方法取得了最好的效果,在太湖数据中,相比于孪生网络,SVM,CNN,GLCMCNN和传统残差网络,本文方法的OA分别高出了50.60%,20.25%,7.00%,3.74%和2.44%,Kappa值分别高出了66.16%,25.47%,9.01%,7.94%和1.39%;在巢湖数据中,相比与孪生网络,SVM,CNN,GLCMCNN和传统残差网络,本文方法的OA分别高出了41.41%,13.57%,9.68%,7.02%和2.30%,Kappa值分别高出了62.94%,23.57%,16.06%,11.39%和3.52%。孪生网络是将两个输入映射到统一特征空间中,提取相似特征,由于没能有效提取不同类别的地物特征,导致其精度偏低;SVM属于传统机器学习,提取的特征属于浅层特征,高光谱图像中的深层特征没有得到充分利用,影响了其分类精度;CNN模型和GLCMCNN模型精度低是因为高光谱图像输入样本尺寸偏小,导致CNN模型的网络层数被限制,不能充分提取到高光谱图像的深层特征;传统的残差网络由于加深了网络层次,可以进一步提取高光谱图像中的深层特征,获得了较高的精度,但是由于它只是将每层提取的特征输入到下一层残差单元,不同层之间的特征没有进行深度融合和挖掘,限制了高光谱图像分类精度的进一步提升;本文方法通过采用残差网络提高网络深度,并利用其捷径连接解决由于加深网络导致的梯度消失问题,提高了图像分类精度;同时利用反卷积扩大特征图,并且通过多尺度融合算法使不同层的特征进行深度融合,不仅解决了网络层数被限制的问题,还充分挖掘高光谱图像中的深度特征信息进一步提高了分类精度,因此获得了最高的分类精度。

表5 不同方法的对比结果Tab.5 Comparison results of different methods
图8所示为可视化结果,图中(a)和(c)分别为太湖和巢湖经裁剪后的原始图像,(b)和(d)分别为本文方法在太湖和巢湖数据集进行分类后的可视化结果,从图中可以看出,本文方法取得了较好的分类效果。

(a)太湖原图像 (b)太湖可视化结果 (c)巢湖原图像 (d)巢湖可视化结果
2.4 参数对实验影响
2.4.1 卷积核个数对实验的影响
在深度学习中,卷积核个数与最终的分类精度并不是成正比的,该参数的设置尚未有明确的理论支持,本文采用根据经验值设置候选值,并通过实验分析确定最优的卷积核个数。一般而言,残差网络中第一层网络中卷积核个数为16,本节做了第一层卷积核个数分别设置为8,16,32和40分别进行5次实验,结果如表6和表7所示。

表6 不同卷积核个数下太湖数据的分类结果Tab.6 Classification results of Taihu Lake data under different numbers of convolution kernels

表7 不同卷积核个数下巢湖数据的分类结果Tab.7 Classification results of Chaohu Lake data with different numbers of convolution kernels
可以看出:
1)卷积核个数为16时比卷积核个数为8时的精度高,验证了候选值的可靠性。
2)卷积核个数为32时精度最高,太湖和巢湖数据集卷积核为32时比卷积核个数为16时的总体分类精度上分别提高了3.16%和1.11%,在Kappa系数上也分别提高了2.64%和1.65%。
3)在卷积核个数为40时精度比卷积核个数为32时在太湖和巢湖数据上分别降低了4.03%和1.83%。综合考虑本文卷积核个数采用32。
2.4.2 输入大小对实验的影响
本文中输入样本是以某一像素点为中心、以N×N(N为奇数)的邻域块作为二维卷积神经网络的输入,图像分类中邻域块的分类结果作为中心像素点的类别。样本输入大小不同会影响高光谱图像分类精度,本节主要讨论15×15,25×25,27×27和29×29这4个不同输入对太湖和巢湖的影响,表8和表9分别为太湖和巢湖在不同输入的分类结果,从表8中可以看出在输入为27×27时精度最高,而表9中是输入为29×29时精度最高,比27×27时提高了0.9%,但是随着输入尺寸增加计算成本也会随之增加,综合考虑分类精度和计算代价,本文算法选取了输入大小为27×27。

表8 不同输入大小下太湖的分类结果Tab.8 Classification results of Taihu Lake under different input sizes

表9 不同输入大小下巢湖的分类结果Tab.9 Classification results of Chaohu Lake with different input sizes
3 结论
为进一步充分挖掘高光谱图像中的深层特征,本文提出基于残差网络特征融合的高光谱图像分类方法,利用残差网络中残差单元进行特征提取,通过其恒等映射的特点加深网络层数,利用反卷积扩充特征图,并通过融合不同尺度的特征实现高光谱图像的深度特征提取和融合。实验结果表明,与其他学习方法相比,本文方法获得了最好的分类性能。具体总结如下:
1)高光谱图像蕴含丰富的地物图谱信息,传统机器学习只能提取浅层特征,不能充分利用高光谱图像中的深层特征影响了其分类精度的提高;而深度学习技术由于其良好的深度特征提取能力获得了较好的分类效果。
2)传统残差网络可以利用其恒等映射特点加深网络层数,解决了高光谱图像分类中由于样本输入尺寸偏小导致的网络层数有限的问题,同时缓解了由于网络层数加深容易出现的梯度消失问题,可以进一步深度提取地物特征,提高了高光谱图像的分类精度。
3)本文方法充分利用了残差网络在加深网络层数、缓解梯度消失方面的优势,并结合反卷积通过填充信息扩大特征图、进行不同维度的特征图多尺度有效融合,实现层与层之间的深层特征互补,深度挖掘并充分利用高光谱图像中的深层特征信息,进一步提高了高光谱图像分类精度。
本文方法主要是针对高光谱图像进行分类,但是目前高光谱传感器由于时空分辨率的限制,有些区域的高光谱图像难以获取,为满足更广泛的地物分类识别,充分利用高空间分辨率、高光谱分辨率及高时间分辨率的遥感数据进行多源数据融合是我们接下来的研究方向。

