洪水诱导下尾矿库溃坝数值模拟及灾害分析

余国平，唐笑，肖利兴

（中国瑞林工程技术股份有限公司,江西南昌 330038）

随着矿业资源开发的日益激烈，尾矿库库区的安全稳定问题引起广泛关注。据统计，2001—2015年我国发生尾矿库事故99起[1]。在不同诱导因素作用下，尾矿库易发生滑坡、失稳等重大灾害，严重侵害到尾矿库下游居民生命、财产安全。因此，对尾矿库的溃坝致灾机理及洪水灾害规律研究显得尤为重要。近两年，在尾矿库溃坝风险性评估方面，董译萱等[2]通过提出博弈论—有限元模型的溃坝风险评价方法，对河南省的5个尾矿库进行了风险性评价。柯丽华等[3]建立了基于可拓层次分析法（EAHP）的尾矿库溃坝风险多级模糊综合评价模型，并将其应用到杨家湾尾矿库在坝体失稳和洪水漫顶的风险性评价中。在溃坝数值模拟方面，刘晓峰[4]采用CFD软件对尾矿库漫顶溃坝进行数值模拟，分析研究了溃坝过程及其对下游的影响程度。孙银华等[5]利用Fluent数值模拟软件对云南某矿库的溃坝过程进行了三维仿真模拟，探究了尾矿库溃坝对下游建筑物的影响。杨蓉等[6]利用溃坝问题的数学模型和Fluent软件对尾矿的溃坝过程进行了三维地形数值模拟研究，分析了尾矿库溃坝时尾矿砂浆的运动特点。在模型试验方面，张修照等[7]对广东某尾矿库发生洪水漫顶溃坝事故进行了详细描述，分析了溃坝原因及灾害特点。罗昌泰[8]通过模型试验，系统分析了整个溃坝过程中的坝体失稳的形态变化及水砂流的淹没范围，探究了水砂和溃坝流场的演进过程。杨玉婷等[9]借助自制的尾矿库溃坝试验装置，开展了尾矿库的室内堆（溃）坝模型试验，研究了渗流破坏情况下尾矿库溃坝过程、溃口发展、下泄泥砂沉积规律。

为探讨洪峰致灾诱导下尾矿库的溃坝过程及水体淹没成灾规律，本文拟利用Flow-3D数值模拟软件对国内南方山区某尾矿库的溃坝过程进行拟仿真模拟，探究不同断面的流量时程变化及流体波及范围，探究关键监测点的水位变化及致灾规律。研究成果可为类似尾矿库的溃坝防治及灾害救援提供参考。

1 工程概况

根据国内南方山区某矿特点，尾矿坝采用改良中线式废石堆积坝形式。其中，初期坝采用斜墙堆石坝，后期采用复合堆积坝。复合堆积坝选用垂直心墙进行防渗。随着心墙下游井下排出废石逐年加高，心墙上游选矿排出的尾矿逐年堆积上升，形成下游一半为堆石坝、上游一半为复合堆积坝的状况。尾矿坝目前高程为90 m，平均下游外坡比为1∶3.4，坝顶宽为8 m，库内干滩长度为150 m。尾矿库总容量为3.07×106m3，有效库容为2.4×106m3，剩余库容为0.2×106m3，正常运行水位标高为86.4 m，库区汇水面积为0.8 km2。该尾矿库在建设初期距离城区3 km，但随着城市的不断扩张，目前尾矿库下游数百米范围内分布着各类工厂、学校、医院及居民社区等，一旦发生尾矿库溃坝，后果不堪设想。

2 建模

本研究选用Flow-3D软件对该尾矿库进行三维溃坝数值仿真模拟，并针对尾矿库可能遭遇的最大洪水(简称PMF)或库内事故高水位引发坝坡失稳破坏的情况，做如下假设：1)最大暴雨(简称PMP)中心可能位于尾矿库所在流域或库内人为蓄水水位到同等高程；2)不考虑最大暴雨对下游城区的叠加影响；3)不考虑下垫面渗水及城市地下管网的洪水吸纳情况；4)选用跨坝顶的最小安全系数滑弧。

2.1 理论依据

溃坝的流体模拟采用的基本方程为不可压缩黏性流体的NS方程组，转化为VOF(流体体积分数)形式后，其控制方程的连续性方程表达式为:

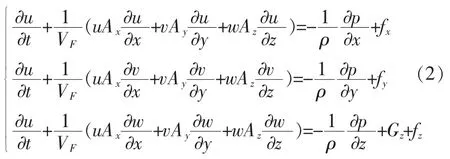
动量方程组为:

式中：ρ为流体密度；下标x、y、z代表各物理量在空间上3个方向的分量；u、v、w分别为x、y、z方向的速度；p为流体微元上的压力；VF为流体微元的体积分数；A代表流体微元在各方向的面积分数；考虑z方向为铅垂方向，则Gz为重力项，f为各方向的黏性项。

摩阻项的表达式为：

式中：τij为作用于流体微元的剪应力；i为作用面；j为作用方向，其大小由各向同性三维黏性流体本构关系确定。

2.2 建模建立

2.2.1 几何模型建立

依据无人机航拍获取的地面信息参数，经专业软件处理后得到以地表信息为基础的曲面，再利用软件将曲面转化为实体；根据坝体下游区域的建筑分布及高程特性，在三维实体上建立建筑模型；将所有三维模型导入Flow-3D中得到其几何模型。本模型采用预制溃口模式，将通过坝顶滑弧且安全系数最小的滑动面作为失稳形成破坏的区域。该滑动面最深处达21.5 m，过坝顶位置垂直深度为5 m。模拟计算对象有效坝长为290 m，溃口宽度取100 m，坝体滑动体形状为楔形。

2.2.2 计算条件

为了解溃坝后下泄洪水对下游城市区域的灾害影响，计算工况设定为：尾矿库处于正常蓄水位运行工况下，遭遇可能最大洪水，并在坝顶发生滑坡；前期洪水正好填满调洪库容，即库内水位正好位于滑坡库内出口，遭遇最大洪水后立即开始冲刷。

2.2.3 参数设置

由于堆石坝发生滑坡后，尾矿库内会出现水流对尾砂的冲刷及尾砂输移、沉积等问题，因此设定重力加速度g=－9.81 m/s2。湍流模型采用Renormalized group模型。计算模型的网格精度为5 m，在此基础上采用非均一网格划分方法，将地表建筑物与水面所在高程区域的网格精度加密至0.5 m，总网格数控制在500万个左右。计算模型的区域边界共计16个，具体设置如表1所示。

表1 模型边界设置

2.3 测点布设

为直观地了解尾矿库下泄流量过程线、下泄洪水总量、下泄尾砂总量，模拟过程中在尾矿库溃口区域及下游计算边界区域各布设1个监测断面。因尾矿库下游城市建筑较多，须关注区域水深与时间、流速的变化情况，计算中选取受影响较为严重、人口较稠密的地区作为监测点。仿真计算模型如图1所示。

图1 仿真计算模型

3 结果分析

3.1 断面流量分析

溃口断面、边界断面的流量随时间变化曲线如图2所示。

图2 断面流量监测时程曲线

由图2(a)可知，溃坝初期，库内水头较高且坝体外坡平顺，流量增长迅速。在溃坝发生60 s时，溃口流量达到最大值1 183 m3/s；在溃坝发生900 s时，溃口流量下降至3 m3/s，随后基本断流。全过程下泄洪水总量为39.2×104m3。

由图2(b)可知，溃坝发生3 000 s后，水流开始影响监测区域，但流量较小；在1 300～2 800 s内，通过监测断面最大流量仅为4.5 m3/s，平均流量约为1.6 m3/s；在2 800～3 600 s内，流量增大至13.2 m3/s，整体处于较低水平。通过监测发现全过程洪水断面总量为7 340 m3，对监测断面后的城市社区影响较小。

3.2 溃坝水淹范围及水深分析

有限元模型中溃坝流体在不同时刻的实时动态如图3所示。图3分别给出了溃坝后360 s、960 s、1 800 s、3 600 s时的水淹范围及水深情况。

由图3(a)可知，水流影响最大的社区为监测点A小区。由于建筑物阻挡，社区短时间内局部积水深度为1.9 m。随着城市行洪的波及，监测点C图书馆短时间内积水深度达1.7 m。由图3(b)可知，随着溃坝水体进一步发展，城区过水面积增大，水位深度整体较小，局部达到1.5 m，且均为积水。由图3(c)可知，库内水位已回落至安全水位，溃口流量低于10 m3/s，对下游影响较小。此时下游区域处于退水期。城区局部区域因为地势低洼或建筑隔断，后期仍存在积水严重问题，平均水深1.5 m。由图3(d)可知，城区过水面积达到峰值，后期不再增大，主要以边界流出为主。

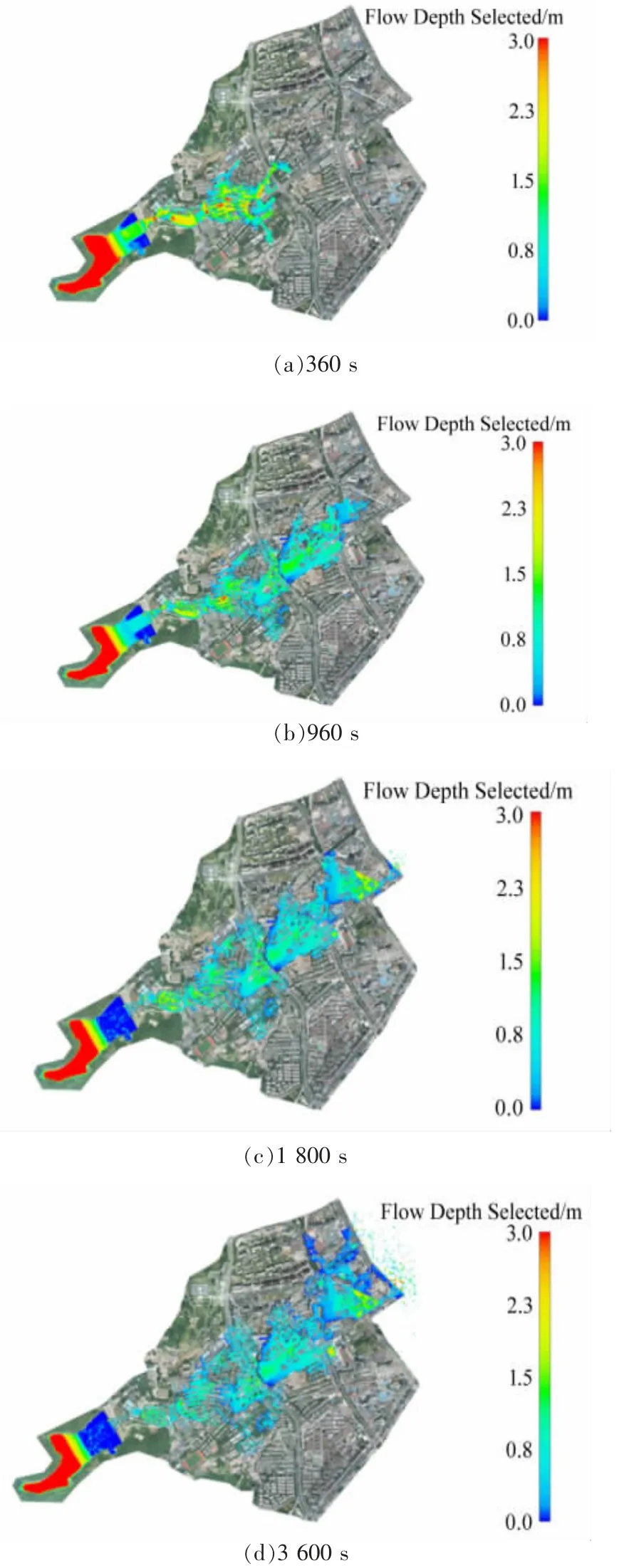
图3 不同时刻水淹范围及水深分布云图

模拟结果显示，溃坝后的洪水淹没范围与水流方向、地势高程、房屋等障碍物的分布密度、可行洪的道路位置等因素有关。与尾矿库水流方向直对、房屋分布密度较大的A小区受灾最严重，但也一定程度上减缓和阻碍了水流扩散。个别主干道具有较大的行洪能力，加速了洪水分洪速度，有效地提高了退水效率，但受溃坝洪水冲击影响也是最大的。

3.3 监测点水深变化分析

根据计算结果，因监测点B中学和E中学在溃坝期间未受洪水影响，因而图4仅给出监测点A小区、C图书馆、D幼儿园的水深变化时程曲线。

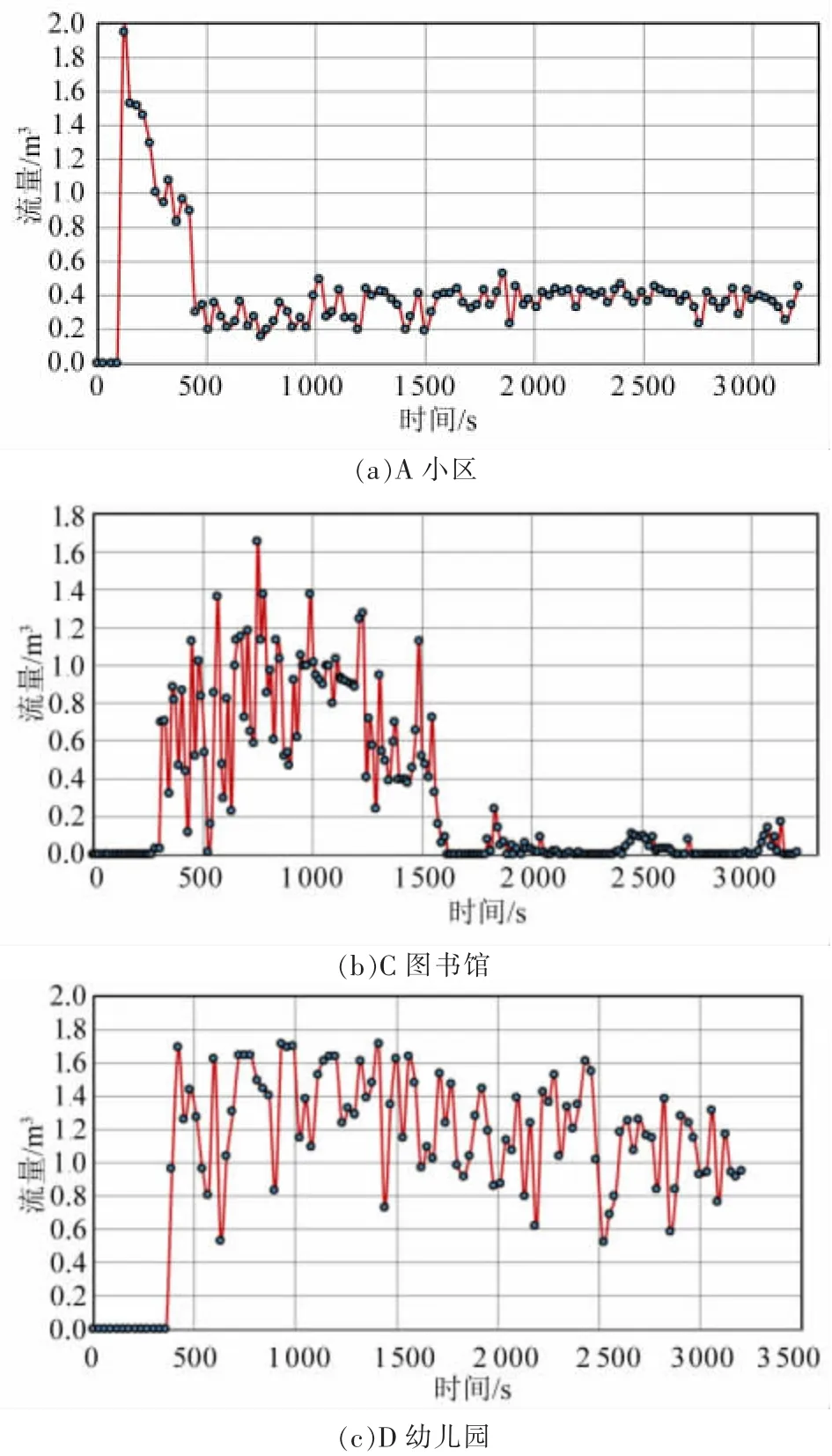
图4 监测点水深变化时程曲线

由图4(a)可知，A小区最先受到水流冲击，洪水起涨点的时间＜60 s，在溃坝发生120 s后，积水深度升至峰值1.9 m，随后在420 s内下降至0.2 m。整个过程中，水深超过0.4 m的持续时间为540 s。图4(b)中监测点C图书馆处的洪水起涨点的时间在溃坝后300 s，溃坝发生后750 s后，积水深度达到峰值1.7 m。整个过程中，溃坝发生后300～1 600 s时间段内积水深度超过0.4 m。溃坝发生后1 600 s后，水流基本退去。图4(c)中监测点D幼儿园在溃坝发生420 s后开始受水流影响，积水水位在1.2～1.7 m间波动，且在溃坝模拟时间范围内未完成退水，最终积水深度为1.0 m。

4 结论

本文通过对某尾矿库在洪水作用下的溃坝灾害进行了数值仿真模拟，得到以下结论。

1)模拟总时长3 600 s，其中溃坝历时900 s，造成下泄洪水水量为39.2×104m3。溃坝后的3 600 s内影响范围主要集中在下游400 m内，泄洪边界距离尾矿坝脚2.0 km，最大下泄流量1 183 m3/s。

2)坝脚下游400 m范围内包括坝后缓冲区及A小区受灾最严重，主要表现为洪水起涨时间点快，淹没水深高，冲刷流速大，退水效率低。由于房屋的阻碍消能作用，短期内该区域造成壅水，缩短了下游的洪水起涨时间。

3)溃坝后部分城市主干道成为泄洪主要通道，城市次干道及支路为次要通道，提高了退水效率，可以保证在溃坝发生3 600 s内完成退水，但在行洪过程中可能会波及路侧地势较低位置，造成较深的淹没积水。

4)低洼地区洪水起涨后，水流流速减缓，淹没水深大，局部区域最大水深达1.9 m。由于其形成积水时间长，需要较长的退水时间，实际情况中更依赖城市地下管网的后期排水能力。