一道立体几何轨迹问题的探究

华东师范大学第二附属中学(201203) 戴中元

一、一道立体几何轨迹问题

例1与正方体ABCD−A1B1C1D1的三条棱AB、CC1、A1D1所在直线的距离相等的点( )

A.有且只有1 个 B.有且只有2 个

C.有且只有3 个 D.有无数个

分析为叙述方便,后面所述AB、CC1、A1D1为正方体三条棱所在直线,其中任何两条直线都是垂直的异面直线.容易看出正方体剩下的两个顶点D,B1到这3 条直线的距离都等于正方体的棱长,这是因为AA1是AB、A1D1的公垂线段,BC是AB、CC1的公垂线段,C1D1是CC1、A1D1的公垂线段.再根据对称性可知正方体的体心Q到这三条棱的距离也相等.这三点都满足要求,距离随着点的移动连续变化,所以猜想体对角线DB1上的点都满足要求.

解答下面证明体对角线DB1上任何一点P到三条棱AB、CC1、A1D1的距离相等.过点P作PQ⊥ABCD于点Q,PR⊥AB于点R,因为DB1在平面ABCD上的投影为DB,故Q点在面对角线DB上,且PQ⊥QR,所以∆PQR是直角三角形.同理也可以作PS⊥CDD1C1于点S,PT⊥CC1于点T,可得直角∆PST;作PU⊥ADD1A1于点U,PV ⊥A1D1于点V,可得直角∆PUV.因为P是体对角线上的点,所以PQ=PS=PU,QR=ST=UV.故∆PQR,∆PST,∆PUV是全等三角形,所以PR=PT=PV,即P到三条棱AB、CC1、A1D1的距离相等,所以选D.

上述解答解决了满足要求的点的个数有无穷多个,除了以上点之外还是否有其他点呢? 下面我们就来探讨这个问题.

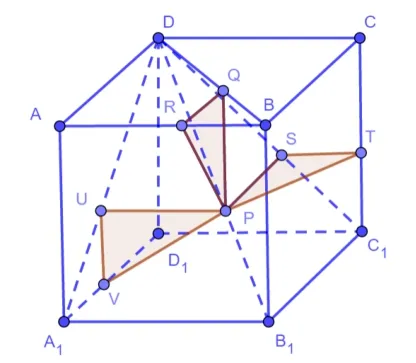
图1

图2

二、到两条垂直异面直线距离相等的点的轨迹

问题1在空间中,l1,l2是两条距离为2 的垂直异面直线,求到这两条直线距离相等的点的轨迹.

该类曲面为双曲抛物面,因形状类似于马鞍,也称为马鞍面.当用平行于xoy的平面去截马鞍面可以得到双曲线,例如用平面z=k去截上述双曲抛物面可得等轴双曲线x2−y2= 4k,特别地,当k= 0 时,截得的曲线是两条相交直线.当用平行于yoz的平面或者平行于zox的平面去截可以得到抛物线,例如用平面x=k去截双曲抛物面可得抛物线y2+4z=k2.所以可以得到如下结论:

定理设直线l1,l2是垂直的两条异面直线,平面α//l1,l2且α到l1,l2的距离相等.

例2(2004年高考北京卷) 在正方体ABCD−A1B1C1D1中,P是侧面BB1C1C内一动点,若P到直线BC与直线C1D1的距离相等,则动点P的轨迹所在的曲线是( )

A.直线 B.圆 C.双曲线 D.抛物线

解答因为P是BB1C1C内一点,所以P到C1D1的距离即为P到点C1的距离,所以在平面BB1C1C到直线BC和点C1(不在BC上)的点P的轨迹是以C1为焦点,为准线的抛物线.故选D.根据上述定理或直接推导可得

变式1 若将“P是侧面BB1C1C内一动点”改为“P是平面A1B1C1D1内一动点”,那么P点的轨迹是以B1C1为实轴,C1D1为虚轴,且以B1为一个焦点的等轴双曲线.

变式2若将“P到直线BC与直线C1D1的距离相同”改为“P到直线BC与直线C1D1的距离之比为1:2(或2:1)”,则动点P的轨迹是椭圆(双曲线).

图3

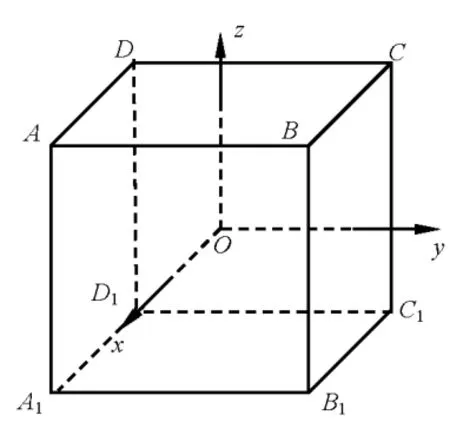
图4

三、到三条直线(其中任何两条直线垂直且异面)距离相等的点的轨迹

四、到空间中一直线及直线外一点距离相等的点的轨迹

五、到空间中一平面及平面外一点距离相等的点的轨迹

若将问题4 中的一条直线改为一个平面,可提出如下问题.

六、其他类似问题

问题5 求到空间中三点距离相等的点的轨迹.

解答(1)若这三点共线,则满足要求的点不存在.(2)若三点A,B,C不共线,则确定平面α,点的轨迹是过∆ABC外心且垂直于平面α的直线.

和上述问题类似,可以提出下列问题,供读者思考.

问题6(1)求到空间中一条直线和直线外两点距离相等的点的轨迹.(2)求到空间中两条直线和直线外一点距离相等的点的轨迹.

问题7(1)到空间中两个平面和一条直线距离相等的点的轨迹.(2)到空间中两条直线和一个平面距离相等的点的轨迹.

问题8(1)求到空间中三个平面距离相等的点的轨迹.(2)求到空间中一个平面,一条直线和一个点距离相等的点的轨迹.