以“不变”应“万变”,寻找几何变换的着力点——以“2020年嘉兴中考题”为例

广东省中山市东区松苑中学(528400) 张青

“平移、翻折、旋转”是初中三大重要的几何变换,学生面对“复杂的图形”和“变换的过程”经常“望而生畏”,殊不知在变换过程中只是图形位置变了,隐藏了很多“不变”的知识,学生需要认真领悟其中的数学知识和思想方法,以不变应万变,本文以2020年浙江嘉兴和舟山中考第23 题为例,探讨初中“平移翻折旋转”相关教学内容.

1 试题呈现

在一次数学研究性学习中,小兵将两个全等的直角三角形纸片ABC和DEF拼在一起,使点A与点F重合,点C与点D重合(如图1),其中∠ACB=∠DFE=90°,BC=EF=3cm,AC=DF=4cm,并进行如下研究活动.

活动一:将图1 中的纸片DEF沿AC方向平移,连接AE,BD(如图2),当点F与点C重合时停止平移.

图1

图2

【思考】图2 中的四边形ABDE是平行四边形吗?请说明理由.

【发现】当纸片DEF平移到某一位置时,小兵发现四边形ABDE为矩形(如图3),求AF的长.

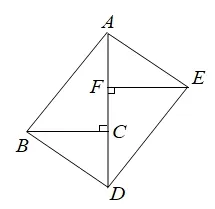
图3

活动二:在图3 中,取AD的中点O,再将纸片DFF绕点O顺时针方向旋转α度(0 ≤α≤90),连接OB,OE(如图4)

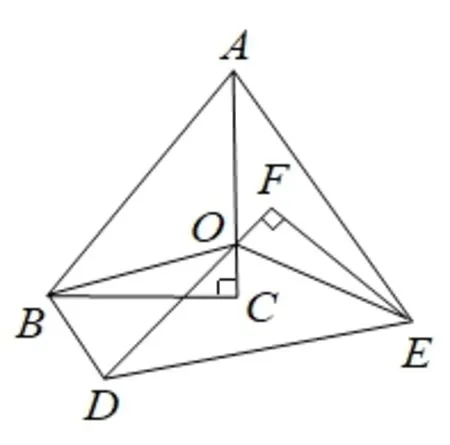
图4

【探究】当EF平分∠AEO时,探究OF与BD的数量关系,并说明理由.

2 解法探究

思考:利用平移的性质不难得到AB与ED平行且相等,得出四边形ABDE是平行四边形.

发现(简解):法1:利用勾股定理解答,设AF=xcm,则AD=(4+x)cm.在RtΔAFE中,AE2=AF2+EF2,因为矩形ABDE,在RtΔAED中,AE2=AD2-EF2,即x2+9=(4+x)2-52,解得.

法 2:利用三角形相似解答(如图 5),在RtΔAFE和RtΔEFD中,利用∠FAE+∠FEA=90°,∠FAE+∠FDE=90°得出∠FEA=∠FDE,得出RtΔAFE∽RtΔEFD,得出,即,得出结果.

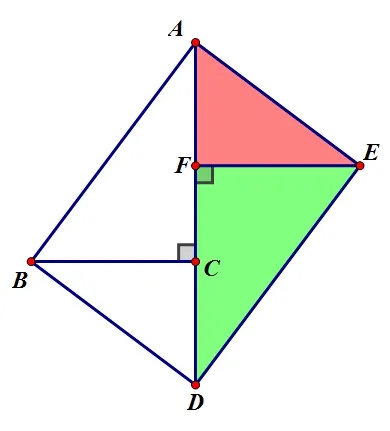
图5

法3:利用三角函数知识解答,方法2 得出∠FEA=∠FDE,在 RtΔAFE和 RtΔEFD中,tan ∠FEA=tan ∠FDE,得出结果.

法4:利用“等面积法”求解,S矩形=2SΔABD=AB·AE,即得出

法5:利用矩形的性质解答,连接BE交AD于点O(如图6),则BO=AO,即BO2=AO2,在RtΔBCO中,即32+解得.

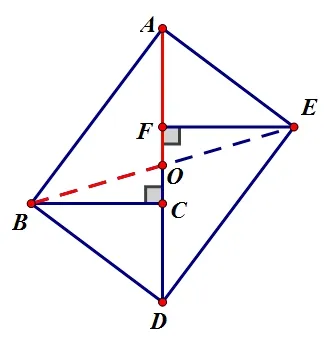
图6

探究:当EF平分∠AEO时,.

法1:延长OF交AE于点G(如图7),由旋转的性质和矩形的性质不难得到∠1=∠2=∠3=∠4,OA=OB=OD=OE,推出∠OBD=∠ODE,∠OAE=∠OEA,由四边形ABDE的内角和为360°得出∠BAE+∠DBA=180°,推出AE//BD,得到∠OGE=∠ODB,根据EF平分∠AEO和直角,利用“ASA”可以得到ΔEFO∽=ΔEFG,得出∠OGE=∠GOE=∠OBD=∠ODB,利用“AAS”可以证明ΔEOG∽=ΔOBD得出.

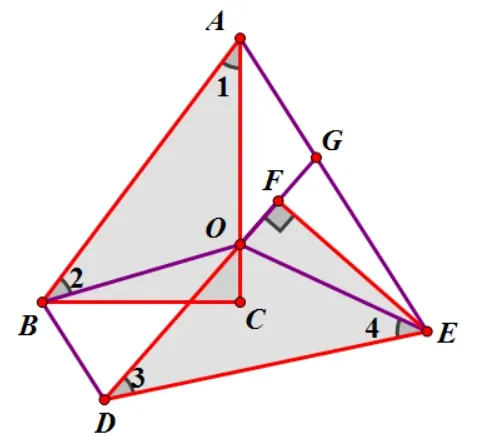
图7

法2:在证明AE//BD,还可以利用OA=OB=OD=OE,推出点A、B、D、E四点共圆(如图8),由“圆内角四边形对角互补”可以得出∠BAE+∠BDE=180°,∠BAE=∠1+∠CAE=∠4+∠AEO=∠DEA,得出∠DEA+∠BDE=180°,推出AE//BD.下面证法与方法1 相同.

图8

3 特色解读

3.1 以“活动”为载体,尊重知识发展规律

本题从活动1 开始将纸片DEF沿AC方向平移,根据平移的性质,在平移的过程中得到一些“不变量”,学生思考后不难判定四边形ABDE是平行四边形,当平移到某一位置时发现四边形ABDE为矩形,相对于思考环节来说,这里涉及的数学知识较多,学生要擅于捕捉“三角形全等”这个不变量和从“矩形的性质出发”,利用思考中的结论“四边形ABDE是平行四边形”可以顺利求出AF的长度,接下来通过活动2 将纸片DEF绕点O顺时针方向旋转,当旋转到某一位置即“EF平分∠AEO”时,.本题设计的数学活动从“平移”到“旋转”这个过程中,顺应了学生的认知发展,设计问题“由浅入深”,尊重知识发展规律,促进学生思维的发展.

3.2 以“人”为本,关注核心素养的培养

本题设计思路清晰,学生在经历数学活动的过程中,经历从“平移”到“旋转”的过程,建立自己的模型,培养了学生直观想象的能力,把数学活动经验转化为相关数学知识的过程,培养了学生的数学抽象能力,在寻求条件和解答问题的过程中,把数学经验转化成数学语言,学生用数学语言表达数学问题时,培养了学生的逻辑推理能力,在利用勾股定理等相关数学知识求线段长度时,提高了学生的运算能力,本题关注了学生的发展,落实了核心素养的培养,既有知识的广度,在发现这个环节体现了思维的深度,凸显了人的教育本质.

3.3 以“不变”为主旋律,畅想解题的“多变”

本题涉及的几何变换有平移和旋转,虽然图形的位置发生了变化,但是在平移和旋转的过程中两个直角三角形纸片ABC和DEF始终全等,学生抓住“全等三角形的对应边相等和对应角相等”这个性质,揭示问题本质,突破解题难点,寻求解题方法,以“静”制“动”,以“不变”为主旋律,在变换过程中找到切入口,在本题中发现的这个环节,抓住“矩形的对角线互相平分”和“三角形的对应角相等”寻找线段之间的数量关系,通过“等量代换”的数学思想,达到解决问题的目的.

3.4 以一“题”多解,适应各类学生的发展需求

《义务教育数学课程标准(2011年版)》(以下简称《课程标准》)指出:“数学课堂的教学要使每位学生都能获得良好的数学教育,不同的人在数学上得到不同的发展”[1].本题的考察的知识有:平移、旋转的性质、平行四边形的判定、矩形的性质、平分线的性质、勾股定理、平行线的判定、四边形的性质等等,涉及的知识较多,学生在解答过程中可以从不同的角度去思考,利用相关知识顺利解答本题,根据不同的思维品质采取不同的方法,涉及到的数学方法有:解析法、面积法、辅助线法、转化法、等量代换等等,学生可以根据自己的基础去选择适合自己的数学方法,找出关键点,达到解决问题的目的,不同层次的学生得到不同的发展.

4 教学建议

4.1 构建有效“问题链”,助推课堂深度教学

问题是数学的心脏,问题也是思维的导火线,有效的问题和教师的有效提问有利于学生基础知识和基本技能的掌握,可以引领学生数学思维深度发展,教师在组织教学时可以设计“问题链”,通过“问题链”的形式组织教学,上面涉及到的中考题就是以“思考—发现—探索”为线索,通过“平移—旋转”数学活动,从“三角形—平行四边形—矩形”中层层递进设置问题,通过“四边形ABDE是平行四边形吗?”引发学生思考,进而利用相关数学知识求线段的长度,进而推测两线段之间的数量关系,引起学生深度思考,教师在课堂教学过程中通过设置“层层深入”、“环环相扣”的问题引发学生深度思考,设置变式问题,发展学生对知识迁移能力,有效构建“问题链”,促进学生高阶思维的发展.

4.2 开展数学实验,感受几何变换中的“不变”

《课程标准》中指出:“在数学活动中,必须通过学生主动的活动,感受做数学的过程,实现再创造的乐趣,从而让数学实验真正走进课堂[1].”教师在开展数学实验时,有利于数学基本活动经验的积累,以往学生对于变换的图形只是从表面上去理解,没有真正感受几何变换过程,教师在课堂教学过程中,可以开展数学实验,选择一些易于学生操作的教具,通过“移一移”、“折一折”、“转一转”等数学实验,让学生在参与实验、猜想、证明等操作过程中,感受几何变换中的“不变”,例如在折纸过程中体验哪些角相等,哪些边相等,在体验的过程中探索数学的本质,在数学实验操作过程中,发展学生的合情推理与演绎推理能力,学会用数学语言表达世界,积累丰富的数学活动经验.

4.3 渗透数学思想方法,让核心素养落地生根

《课程标准》在问题解决中指出:“经历从不同角度寻求分析问题和解决问题的方法的过程,体验解决问题方法的多样性,掌握分析问题和解决问题的一些基本方法[1].”数学思想方法是引领学生学习数学的方向,是学生把数学知识转化为数学能力的基本桥梁,教师在实施课堂教学过程中,注重学生参与分析问题和解决问题的过程,总结不同的数学思想方法,发展逻辑推理和演绎推理的能力,通过“数学活动”等环节培养学生的直观想象能力,提升学生的数学建模能力,真正让核心素养落地生根,以数学思想方法为枝节,促进学生全面发展.