基于Modelica的RAT作动机构仿真及设计参数优化
黄 艳,蔡 景,代定强
南京航空航天大学民航学院,江苏南京 211106
安全性是飞机运行的基本要求,而冲压空气涡轮(ram air turbine, RAT)系统作为最后一道屏障,在飞机发动机和辅助动力装置都失效的情况下为飞机关键部位提供能源[1-6],确保飞机发生故障时仍能被操作,避免事故发生,保障生命和财产安全.民航局规章CCAR-25.671(d)条规定,飞机的设计要保证在所有发动机都失效情况下仍可操纵[7].RAT系统现已在民用飞机上普遍安装,国外对RAT系统的研究较早,技术较为成熟,其中,Dowty[8]和Hamilton Sundstrand公司[9]的研究具有一定代表性;中国的RAT系统大多参考国外设计进行改进,如王永鑫等[10]研究RAT装置在民用涡桨飞机造型中应考虑的因素;周连骏等[11]根据收放装置的工作原理,运用LMS Virtual.Lab Motion构造刚柔耦合的多体动力学模型,并运用AMESim构造作动机构液压模型,将两种模型关联从而实现联合仿真;夏天翔等[12]对RAT系统建立多学科模型,仿真其在不同工况和设计参数下的动态特性,并结合风洞试验验证模型准确性.RAT系统已由原来传统的电或液的形式向电液混合式发展[12],常用的仿真工具主要用于单一领域的仿真建模,并不适用于RAT系统这一典型机电液综合系统的多领域统一物理建模,同时目前国内尚缺乏对实现RAT展开任务的核心部件(即作动机构)的相关研究[13].
为改进目前仿真工具单一建模及作动机构方面的不足,本研究选用面向对象的适用于多领域建模的Modelica语言对作动机构进行仿真研究[14],通过实际情况得出故障模式,建立故障树,并确定影响RAT作动机构性能的主要组件.对影响作动机构展开时间和液压油压力的因素进行敏感性分析,并结合Mworks和Matlab从设计方面提出改善措施以控制故障发生.
1 RAT作动机构故障分析
由于使用环境和贮存时间等因素影响,RAT作动机构的可靠性可能发生退化,从而产生各类故障.进行根原因分析能确定影响机构性能的主要组件,以便从设计方面进行改进,减少故障产生的可能.
民用飞机常用的桨叶式RAT作动机构一般处于收回状态,作动机构展开弹簧处于压缩状态且被装置锁定,当收到释放信号后,锁定装置解除,展开弹簧伸长,推出作动机构.收放作动机构的结构如图1,按照执行功能的不同可将其分为锁定装置和执行装置两个子系统.
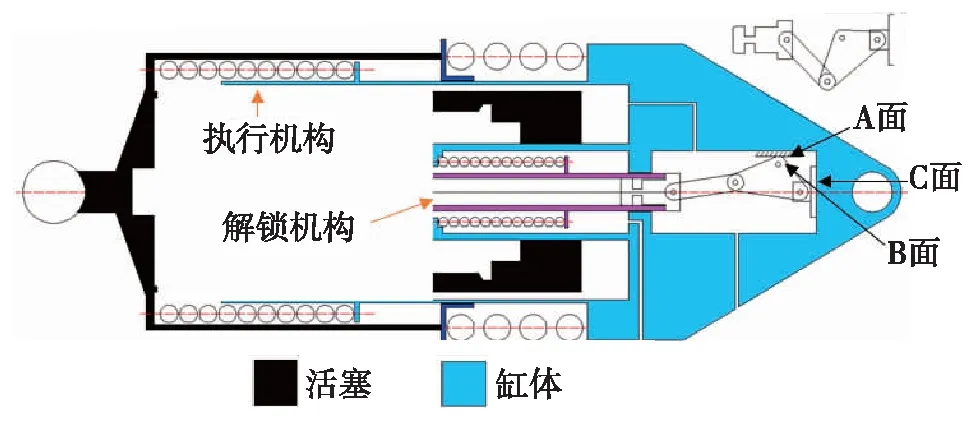
图1 RAT作动机构结构Fig.1 (Color online) Structure of RAT actuator
锁定装置主要由锁定弹簧、平动连杆机构、卡环、钢珠及电磁锁等组成,其包括收起状态的上位锁和伸出状态的下位锁,利用两个卡锁环与活塞上的斜面与凹槽配合以实现锁定和解锁功能.
执行装置主要由展开弹簧、活塞和载荷连接杆组成,通过弹簧力带动整个执行机构产生一定位移,使RAT装置的迎风部分被推出机舱外.弹簧力由两个劲度系数不同的大小弹簧组成,通过这两个弹簧共同作用克服与其他机构的静态摩擦力,确保作动机构的顺利启动.
RAT作动机构通常具有3种展开行程故障模式:① 锁定装置无法解锁展开;② 执行装置展开过快;③ 执行装置展开过慢.针对不同的故障模式,根原因分析能有效识别故障并分析故障原因,便于从根本上提出针对问题本质的解决方案[15].常用的分析方法有事件树分析法[16]、事件因果关系图表法[17]、屏障分析法[18]、树状图法[19]、5-whys 分析法[20]、基元事件分析法[21]及原因图法[22]等.由于故障树分析法全面直观,因此,本研究采用故障树建立作动机构故障模式与其组件之间的关系.
对每一类故障模式分别建立故障树,以执行装置展开慢故障为例,其故障树如图2.其中,GT表示门,即与门或非门等;EV表示底事件;FR表示失效率.对于执行装置展开慢的故障,根原因有密封圈太紧造成的摩擦力过大、杂物卡阻、弹簧储存期间变性、大弹簧提前退出作用、阻尼孔被阻塞及液压油变性等.
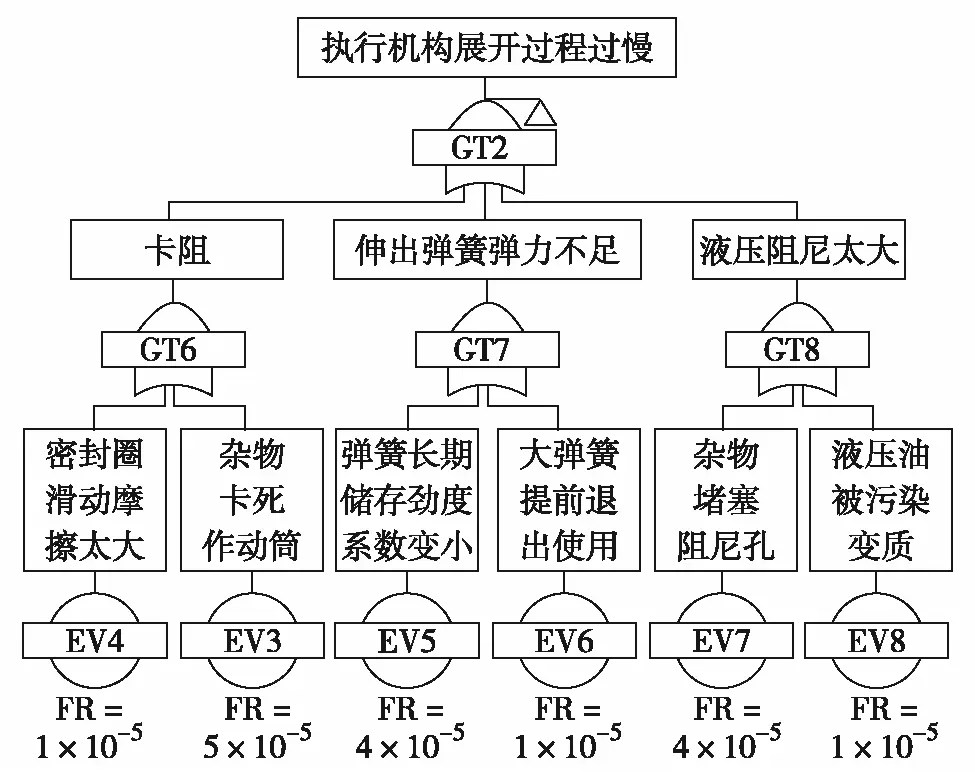
图2 执行装置展开慢故障分析Fig.2 Slow deployment failure analysis of the actuating system
同样对另外两种故障模式建立故障树,结果认为,对于执行装置展开过快的故障,根原因有密封圈失效造成泄漏、阻尼孔磨损变形及液压油变性等;对于锁定装置无法解锁展开的故障,根原因有组件或基体关键表面的磨损或生产装配误差、杂物卡阻、电磁锁失效及液压油变性等.
通过作动机构的故障分析可以看出,作动机构的各类故障模式主要涉及作动弹簧、阻尼孔、密封件以及作动机构结构体本身等因素.密封件的使用一般根据相关标准选取,缺乏改进空间;作动机构结构本体与飞机其他部分联系紧密,不宜调整其结构尺寸.因此,确定作动弹簧和阻尼孔作为可改进的对象,通过优化作动弹簧和阻尼孔参数,实现作动机构性能的改进.
2 基于Modelica的作动机构建模
作动机构的建模包括底层组件建模、整体模型搭建及模型精度验证3个步骤.
2.1 底层组件模型建立
作动机构的底层组件包括风载荷、液压阻尼、弹簧、杆系及机体,其建模可通过利用物理方程组编写模型代码实现,部分简单组件可直接使用标准模型库中的模型.执行装置在展开过程中主要涉及3个力,分别为展开弹簧的弹力、风载荷及液压阻尼[23].其中,展开弹簧的弹力可以根据作动机构的设计数据直接进行参数设置;风载荷源于作用在涡轮上的气流,可直接使用以往的实测数据进行加载;液压阻尼可通过数学方程及作动机构的设计数据计算得出.锁定装置解锁过程涉及的力包括电磁锁的拉力和解锁弹簧的弹力,均按照设计数据取值并设置模型参数.
2.1.1 风载荷建模
使用Matlab工具箱将传感器测量的离散点拟合为4阶多项式函数形式.根据实测数据,得出气动载荷La与作动机构位移d的对应关系,如表1.利用Matlab将表1数据进行4阶多项式拟合,得到气动载荷曲线如图3.拟合函数为
La=-5.14×10-5d4+0.016d3-0.6d2-
88.2d+4 966
(1)
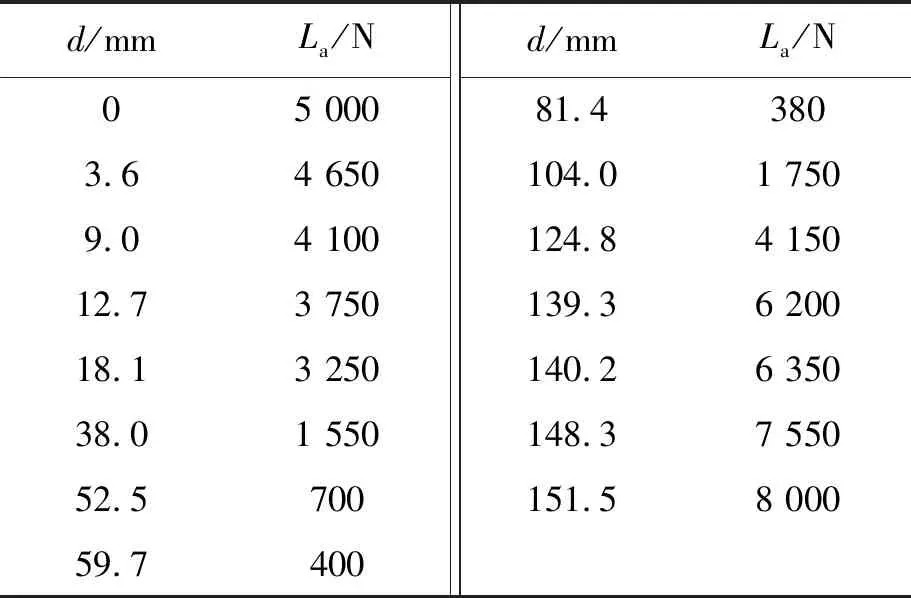
表1 La与d的对应关系Table 1 Corresponding relationship between La and d
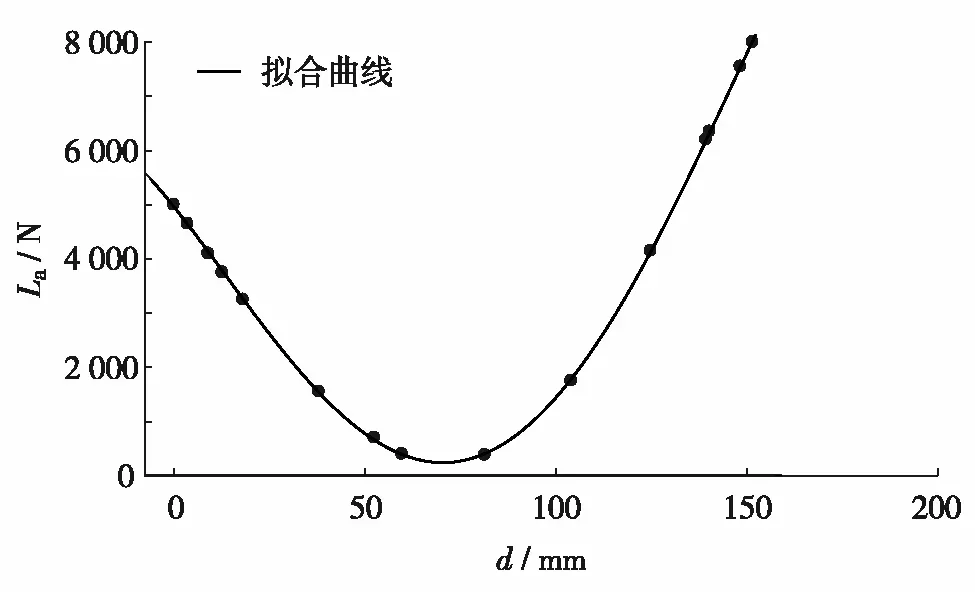
图3 拟合后气动载荷曲线Fig.3 Aerodynamic load curve after fitting
2.1.2 液压阻尼建模
液压阻尼表现为展开过程的阻力,来源于作动机构展开过程的回油阻力.阻尼孔结构与作动机构的展开速度有关,将阻尼孔简化为薄壁小孔,结合薄壁小孔流量公式与活塞的运动学公式,可得
(2)
Q=VApi
(3)
(4)
FW+FS-FO=ma
(5)
FO=pApi
(6)
其中,q为每个阻尼孔的流量;Cd为阻尼系数;A为阻尼孔面积;ρ为液压油密度; Δp为缸内两端压强差;Q为作动机构高压腔总流量;V为活塞速度;Api为活塞面积;a为活塞加速度;m为作动机构质量;FW、FS和FO分别为风载荷、弹簧载荷和阻尼力.液压油离开作动机构腔体后即进入油箱,则腔体外压强为0, Δp即为腔内的实际压强p.
2.1.3 其他组件模型搭建
对于工作原理简单的组件,如弹簧和连杆等,可以直接利用Mworks中已有标准模型库组件进行搭建连接,如使用Modelica.Mechanics.MultiBody.Forces.Spring组件模拟展开小弹簧,设置其劲度系数c=21 500 N/m、 原始长度S=0.3 m.
2.2 作动机构整体模型搭建
利用底层组件搭建作动机构的物理结构并添加相应控制律代码,同时使用自定义连接器在不同子系统之间进行功能信号的传递,实现作动机构整体模型的搭建,如图4和图5,主要建模参数按照实际设计参数取值,如表2.
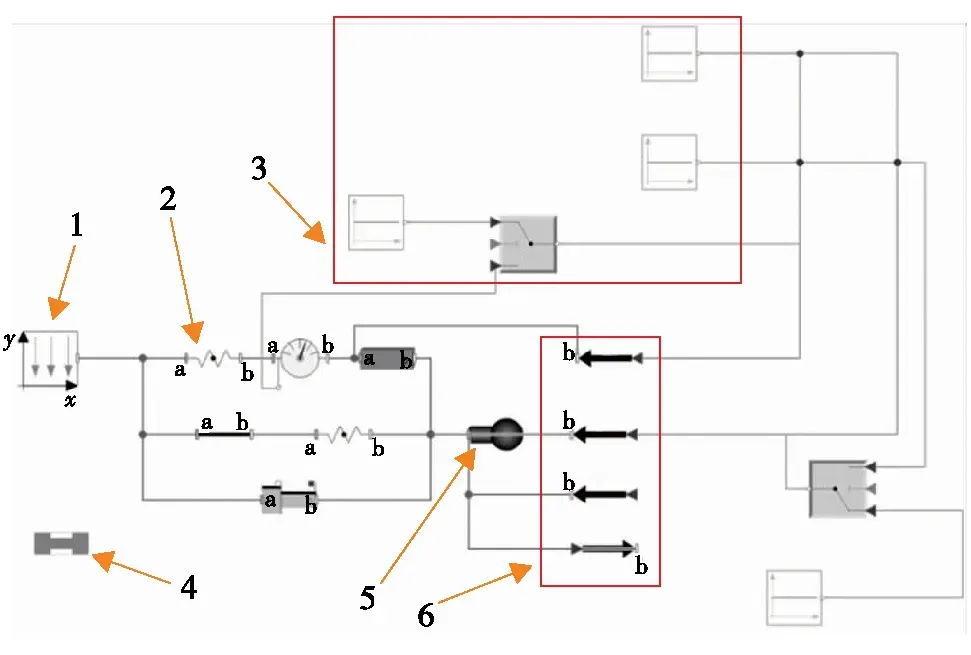
1为弹簧安装固支点;2为展开弹簧;3为弹簧控制器; 4为连接器;5为活塞质点;6为力组件图4 执行装置模型Fig.4 (Color online) Model of actuating system
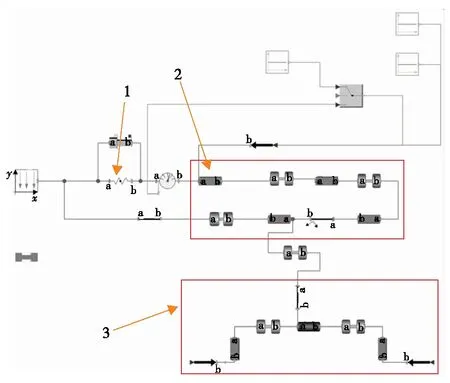
1为锁定弹簧;2为传动杆系;3为电磁拉杆图5 锁定装置模型Fig.5 (Color online) Model of lock system

表2 作动机构实际设计参数
2.3 模型验证
调研知本研究RAT型号的作动机构合理展开范围为0.6~1.5 s.以表1实测状况为工况,表2数据作为Modelica模型初始设计参数,将已建立的作动机构仿真模型结果曲线与某型RAT装置作动机构的实际结果曲线进行对比分析,以确定仿真模型的正确性,如图6.
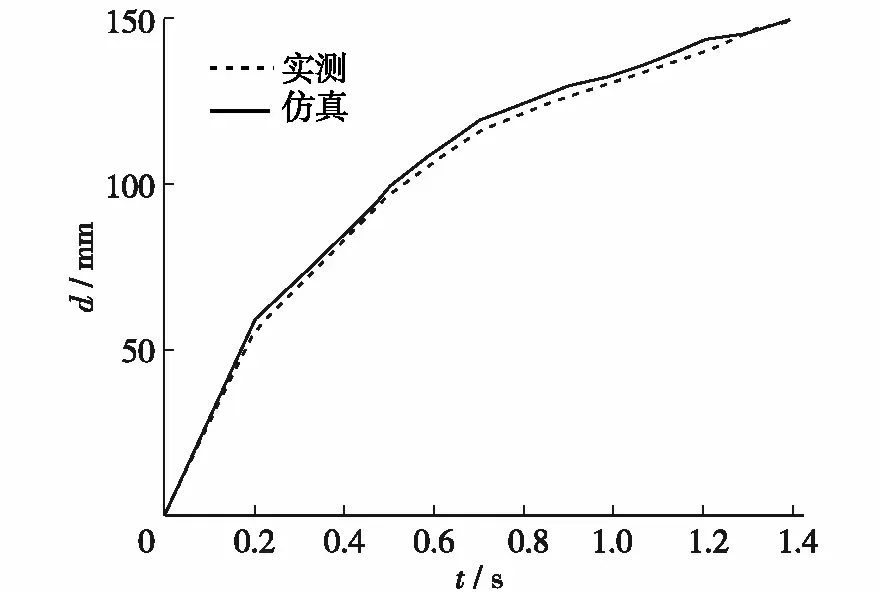
图6 仿真和实测的展开位移-时间曲线Fig.6 Deployment displacement-time curve of simulation and actual measurement
锁定装置解锁成功后,执行装置在作动弹簧力下展开,直至到达目标位移(150 mm).某型RAT作动机构实物试验得出的展开时间为1.32 s,仿真得出的展开时间为1.37 s(解锁时间约为0.04 s),与试验的误差为3.78%.由图6可知,仿真得到的位移-时间曲线与试验测得的曲线较为吻合,证明本研究建立模型的精度较高[10].误差主要来自内外缸密封之间的摩擦力以及风载荷与实际载荷之间的误差.
3 作动机构设计优化及分析
根据作动机构故障分析结果对作动机构的设计参数进行优化,可从根源上减少故障发生.
3.1 设计优化方法
当作动机构展开时的末端速度vend过大时,会导致较大的冲击力以及刚性碰撞,致使释放RAT装置时的安全性和可靠性受到威胁,因此,需要控制vend. 实际试验表明,vend≤0.1 m/s时的冲击力在可接受范围内.同时由于液压油的压力太大会导致液压油泄露以及造成更多的功耗损失,因此,液压油的峰值压强pmax要尽可能小.针对这一问题,提出一种作动机构优化设计方法,为
minpmax(M)
(7)
其中,M表示确定作动机构结构的相关参数集合;pmax(M)表示由参数集合M确定的作动机构在展开过程中的峰值液压(单位:Pa);t为作动机构展开时间(单位:s).
3.2 模型参数敏感性分析
基于作动机构的Modelica模型对作动弹簧和阻尼孔的相关参数进行敏感性分析.使用控制变量法,在保持其他参数不变的情况下,通过仿真逐一分析作动大弹簧劲度系数、作动小弹簧劲度系数、阻尼孔布局间隔及阻尼孔半径对作动机构展开时间和末端运行速度的影响程度,结果如图7和图8.
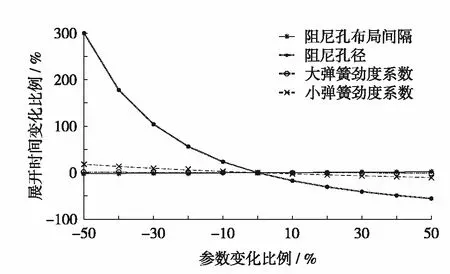
图7 展开时间对各参数的敏感性分析Fig.7 Sensitivity analysis of deployment time to various parameters
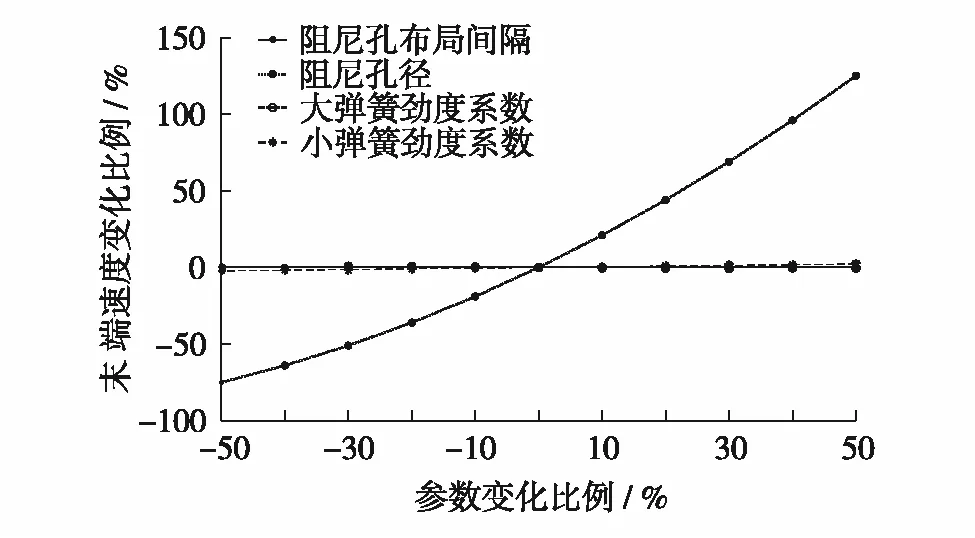
图8 末端速度对各参数的敏感性分析Fig.8 Sensitivity analysis of end speed to various parameters
由图7和图8可见,阻尼孔半径和小弹簧劲度系数对作动机构展开时间和末端速度具有一定影响;大弹簧劲度系数和阻尼孔布局间隔变化造成的影响微小,这是由于大弹簧的作用行程短,对展开过程影响不大;阻尼孔分布位置已接近作动机构行程末端,能造成的影响有限.事实上,当阻尼孔半径减少约5%就会直接造成作动机构展开太慢的故障,如图9.
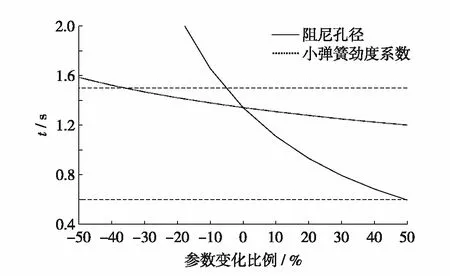
图9 阻尼孔半径和小弹簧劲度系数对 作动机构故障的影响Fig.9 Influence of damping hole radius and spring stiffness coefficient on actuator failure
因此,以下将作动小弹簧的劲度系数c和阻尼孔径r为对象进行优化,即M={c,r}.
3.3 基于展开时间约束的设计优化分析
在Mworks模型中调整小弹簧的劲度系数及阻尼孔半径,确定符合作动机构展开时间相对应的弹簧劲度系数范围和阻尼孔半径范围,对展开时间进行仿真计算,结果如图10.
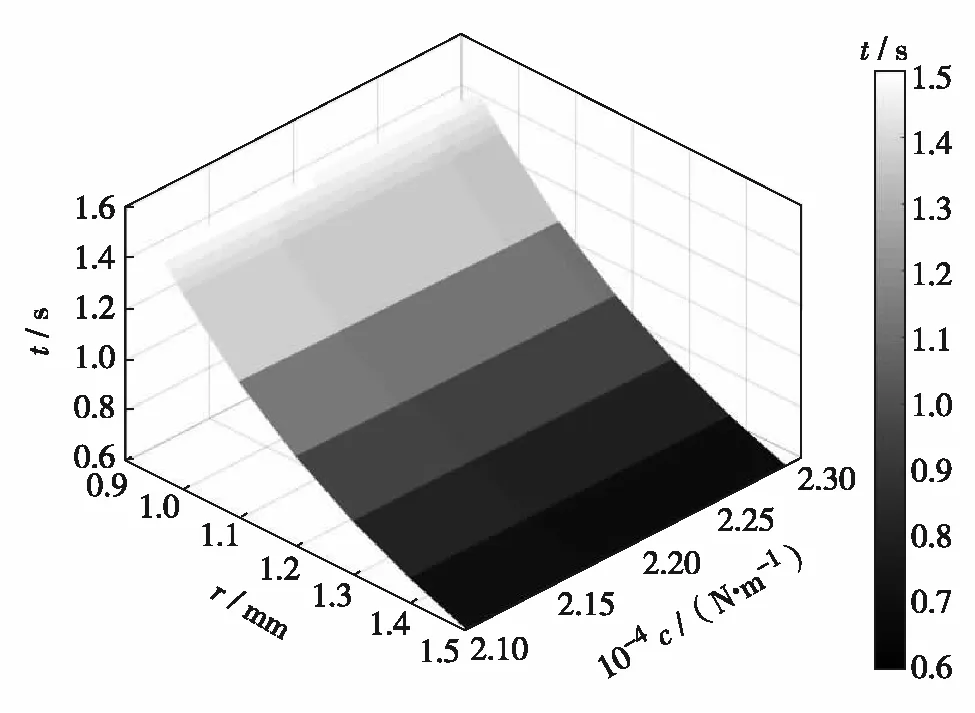
图10 作动机构合理展开时间对应的弹簧劲度系数和 阻尼孔半径范围Fig.10 Spring stiffness coefficient and damping hole radius range corresponding to the reasonable deployment time of the actuator
研究结果表明,当小弹簧的劲度系数为21 000~22 900 N/m、阻尼孔半径为0.96~1.50 mm时,作动机构展开时间在规定范围0.6~1.5 s内.由图10可见,弹簧劲度系数越大,阻尼孔半径越小,则作动机构展开时间越长.由工程实践可知,弹簧劲度系数越大时对应的弹簧展开力越小,阻尼孔半径越大时对应的阻尼力越小,从而使作动机构能更快展开.
3.4 基于展开末端速度约束的设计优化分析
分析作动机构展开末端速度和展开时间之间的关系,结果如图11.可见,随着展开时间增大,末端速度逐渐降低,利用Matlab软件得出拟合方程为
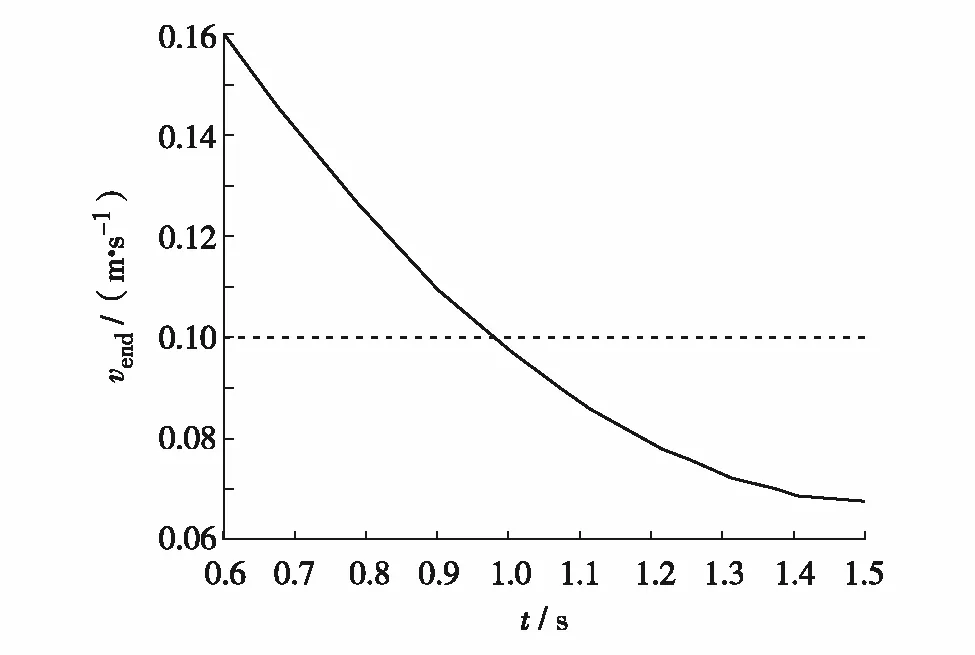
图11 末端速度与展开时间的关系Fig.11 Relationship between end speed and deployment time
vend=0.106 2t2-0.325 8t+0.317 2
(8)
当末端速度为0.1 m/s时,对应时间为0.979 3 s.当作动机构展开时间为0.979 3~1.500 0 s时,对应末端速度符合要求.这个时间段对应的弹簧劲度系数与阻尼孔半径如图12.
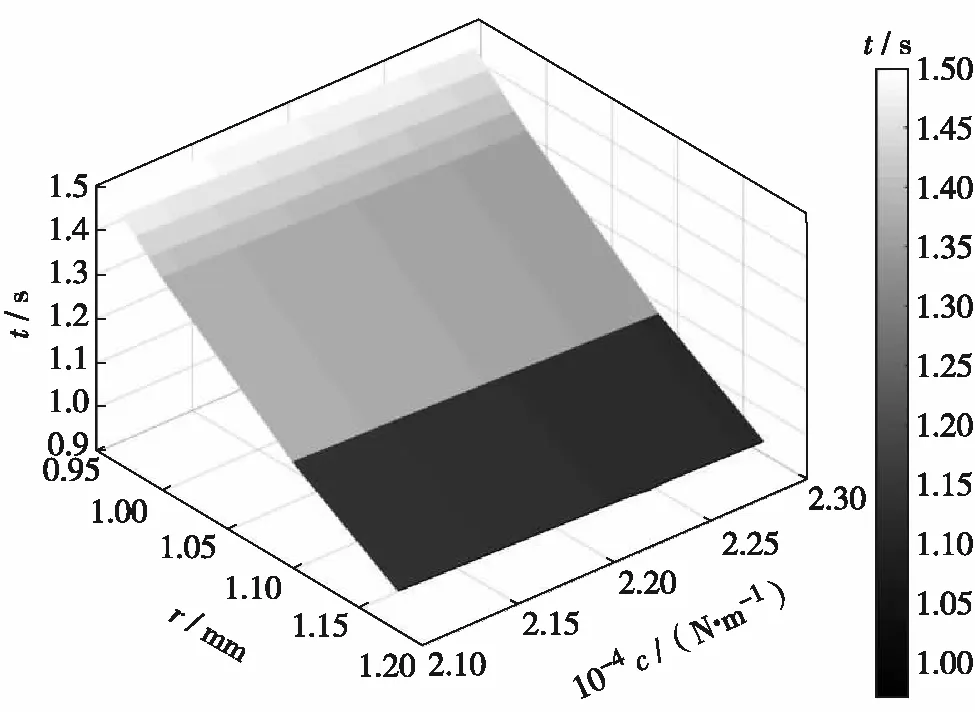
图12 作动机构合理展开时间及末端速度对应的 弹簧劲度系数和阻尼孔半径范围Fig.12 Spring stiffness coefficient and damping hole radius range corresponding to the reasonable deployment time and end speed of the actuator
当弹簧劲度系数为21 000~22 900 N/m、阻尼孔半径为0.96~1.18 mm时,作动机构展开时间和末端速度均符合要求.
3.5 优化目标值确定
对满足约束条件的各不同弹簧劲度系数和阻尼孔半径设计参数下的液压油峰值压力进行统计,部分数据如表3.当阻尼孔半径为0.97 mm,弹簧劲度系数为21 000 N/m时,对应液压油峰值压力值最小.因此,选取该情况下的阻尼孔半径和弹簧劲度系数作为最优设计值.
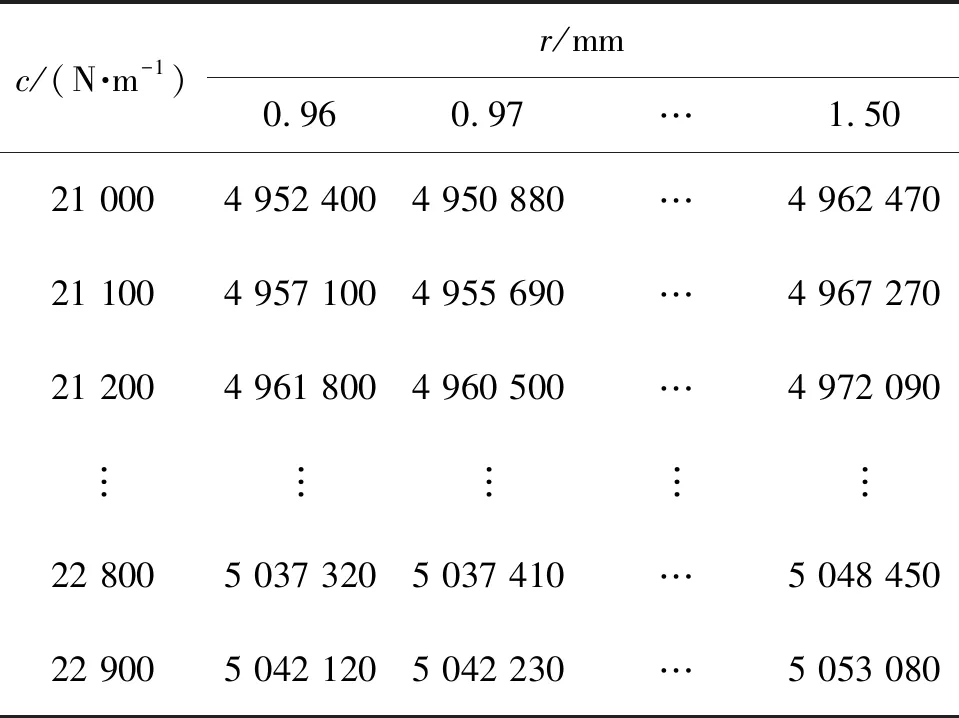
表3 不同阻尼孔半径和弹簧劲度系数下的压力值Table 3 Pressure values under different damping hole radii and spring stiffness coefficients
结 语
为优化RAT系统作动机构的关键设计参数,基于实际使用案例建立故障树,分析导致作动机构主要故障模式的组件.在此基础上,采用Modelica语言对RAT作动机构进行仿真建模,对其主要故障形成机理和各设计参数的定量影响程度进行分析.① 通过故障树分析,确定影响作动机构展开时间的主要组件分别为展开小弹簧以及阻尼孔;② 建立基于Modelica的作动机构模型,通过与实测相比,精度误差仅为3.78%;③ 利用敏感性分析,确定影响作动机构展开的主要组件设计参数为小弹簧劲度系数和阻尼孔半径,并基于作动机构的Modelica 模型,研究作动机构的设计参数优化方法,该方法同样可用于其他RAT型号的参数设计优化,为RAT作动机构的正向设计提供重要基础.

