时态数据质量规则的研究及检测

黄 慧，李海林

1(三江学院 计算机科学与工程学院，南京 210012)2(南京航空航天大学 电子与信息工程学院，南京 211100)

1 引 言

大数据时代，数据质量直接关系数据深层使用价值的实现效果.高质量数据不仅创造着巨额的社会财富，甚至已经关乎国计民生.而劣质的数据会导致决策偏差，社会财富损失，对社会安定和人身安全都形成巨大的威胁[1].近年来，学者们针对数据质量问题展开了广泛的研究，大多研究工作基于函数依赖规则[2-4]，进行不一致数据的检测与修复.函数依赖(FDs)指的是，对于关系R中的属性X和Y，X→Y是一个函数依赖，对于R中的任意两条元组ti和tj，若ti[X]=tj[X]，则必有ti[Y]=tj[Y].依照该规则，不难发现表1中存在不一致数据.

例1.表1中，关系模式Accident(ID，TeaID，TeaName，Level，Title，AccidentType，Salary，VT)由8个属性组成，分别表示为元组编号、教师编号、教师名、等级、职称、教学事故类型、工资和发生教学事故的有效时间.

表1 教学事故信息表(Accident)Table 1 Teaching accident information table(Accident)

为了扩展约束语义，充分发现更多的不一致数据，Fan W等人在函数依赖的基础上进一步扩展，提出了条件函数依赖(CFDs)[5，6]，CFDs通过给定的条件可以发现更为复杂的不一致数据.同时，在CFDs的基础上，学者们又提出了一套推理规则以及公理系统[7-9]，扩展了“并”和“与”语义[10]，用于检测更多不一致数据.文献[11]定义了一种微函数依赖用于提取属性的部分信息，利用提取函数的依赖关系，发现属性中隐藏的错误信息.文献[12]通过定义硬约束、数量约束、等值约束和非等值约束以获取更多的错误数据.文献[13]利用属性值的相似性扩展了函数依赖，用来描述异构数据的一致性问题.文献[14]将CFDs与条件包含依赖结合，用于发现不一致数据.文献[15]基于分布式环境，结合最小通信原则，给出不一致数据的检测方法.此外，其他研究工作提出的数据质量规则还包括编辑规则[16]、修复规则[17]、差分约束[18]可比较约束[19]和否定约束[20]等，从不同角度描述数据不一致问题.

然而，已有的数据质量规则仅适用于静态数据集中不一致数据的发现，忽略了这样一个事实：一些数据会随时间动态演化.如表1中的教师职称、工资、教学事故、等级等信息并非一成不变，而是会随VT值发生变化.但现有的规则难以适用于此类数据不一致性的检测.

例2.表1中存在如下约束语义：

L1：若发生教学事故，且事故类型为A，则2年内，教师编号唯一决定教师工资(即2年内不能加工资，2年后允许工资发生变动)；

L2：对于同一教师，工资随VT值单调增长(即随着时间推移，教师工资不会出现下降)；

L3：对于同一教师，在2012-2017年期间，等级的值随VT值单调递增(即教师等级在其他时间区间，允许等级的值不随时间规律变化)；

L4：5年内，若教师的教学事故累计3次，则Level的值小于等于2.

不难发现，例2中的约束语义有2个特点：①与时态相关.②数据发生演化.而已有的数据质量规则无法表达这样的语义，因此难以发现表1中隐藏的不一致数据.为了扩展约束语义，本文提出了时态数据质量规则，并在此基础上进行不一致数据的检测.

本文的主要工作如下：

1)提出时态数据质量规则(Temporal Data Quality Rules，简称TDQRs)的形式化表达；

2)给出TDQRs相关性质，通过性质去除规则集中冗余的规则以提升检测效率；

3)基于TDQRs，设计等价类划分方法，形成基于时态的不一致数据检测算法，并通过剪枝的策略优化算法；

4)设计不一致数据查询语言，通过查询语言为用户提供不一致检测结果；

5)通过在扩展的Accident数据集上进行实验，验证本文提出方法的有效性.

2 TDQRs的相关定义与性质

2.1 TDQRs的相关定义

针对时态数据质量规则，本文引入如下定义.

定义1.时态数据质量规则TDQRs(Temporal Data Quality Rules).TDQRs是一组基于函数依赖进行扩展的不一致数据检测规则.TDQRs不仅适用于随时间动态演化的数据集，也适用于传统静态数据集.关系模式R上的一条TDQRs规则表示为：

(VT|ω：X→Y，)

其中，1)VT表示有效时间；2)ω为时间算子，可以存储时间值、时间区间或“forever”，用来刻画时态语义；3)X→Y是类似于函数依赖的表达式，与函数依赖不同的是，X和Y的表示可分为3种形式：属性、用户定义函数和逻辑表达式；4)tp为一个条件模板，允许为空.

定义2.子规则.TDQRs中，X和Y可分为属性、用户定义函数和逻辑表达式3类，为区分不同，定义为3种子规则.

子规则1.X和Y均为属性，标记为Rules with Attributes，简称RwA规则.

若对应的是RwA规则，当ω的值为“forever”，且条件模板tp为空时，RwA规则可退化为传统的函数依赖规则.

子规则2.X和Y均为逻辑表达式，标记为Rules with Logic Expression，简称RwLE规则.

需要说明的是，RwLE规则的ω值可以为“forever”或时间区间[a，b]，当为时间区间时，表示在时间起始点a和结束点b的时间范围内属性的值符合偏序的特点.

子规则3.X和Y包含用户定义函数，标记为Rules with Function，简称RwF规则.

若对应的是RwF规则，X或Y可以是一个包含用户定义函数的表达式，条件模板tp分为tpX和tpY，分别表示条件模板的前件和后件.

例3.根据定义2，例2中的L1-L4可由三种子规则表示为ψ1-ψ4，如下所示：

ψ1：(VT|2years：TeaID→Salary，)

ψ2：(VT|forever：ti≼VTtj→ti[Salary]≤tj[Salary]，)

ψ3：(VT|[2012-2017]：ti≼VTtj→ti≤Leveltj，)

ψ4：(VT|5 years：TeaID，COUNT(AccidentType)→Level，<(≥3，≤2)>)

其中，ψ1是RwA规则；ψ2和ψ3是RwLE规则；ψ4是RwF规则.

定义3.时间距离.I是R上的一个实例，对于I上任意两条元组ti和tj在VT上的差值，称为时间距离，记作DIFF(ti，tj).若DIFF(ti，tj)满足ω，记为DIFF(ti，tj)～ω.

例如，表1中t1和t2元组的时间距离为762days，t2和t3元组的时间距离为550days，若ω为2 years，则DIFF(t1，t2)ω，DIFF(t2，t3)～ω.

定义4.一阶等价类(First Equal Class，简称FEC).为了查找不一致数据，将数据集中的数据按照规则对元组进行首次划分归类，得到的不同集合称为一阶等价类.

若ψ∈RwA，则按规则左部X划分，如ψ1得到的一阶等价类有两个，分别表示为FEC1={ti|ti[TeaID]=′001′}={t1，t2，t3，t4}和FEC2={ti|ti[TeaID]=′002′}={t5，t6}；若ψ∈RwLE，则按条件模板tp中的属性划分一阶等价类，如ψ2和ψ3得到的一阶等价类也为FEC1和FEC2；若ψ∈RwF，则按规则左部X中的非聚合表达式划分等价类，如ψ4同样得到一阶等价类为FEC1和FEC2.

定义5.二阶等价类(Second Equal Class，简称SEC).在一阶等价类的基础上，对元组按照规则再次划分归类，得到的不同集合称为二阶等价类.

当ψ∈RwA时，才存在二阶等价类.获取二阶等价类的方法分为5步：1)对给定的一阶等价类，按照VT值对元组进行先后排序；2)查找与条件模板tp匹配的首条元组ti；3)获取集合Ω，Ω={tj|DIFF(ti，tj)～ω}；4)获取Ω中与条件模板匹配的最后一条元组，若有，将该元组设置为ti，重复第3)- 4)步，直到Ω中没有与条件模板匹配的元组为止；5)将第2)- 4)步得到的元组放入一个二阶等价类，并将剩余的元组按照第2)- 4)形成新的等价类，直到所有元组处理完毕为止.

例4.按照ψ1，对一阶等价类集合{t1，t2，t3，t4}再次划分二阶等价类归类，执行顺序为：(a)按照VT排序，集合仍然为{t1，t2，t3，t4}；(b)查找与tp匹配的首条元组为t1；(c)获取Ω1，此时Ω1=φ，将t1放入SEC1；(d)剩余的元组{t2，t3，t4}按照步骤2)继续处理，首条元组为t2；(e)获取Ω2，此时Ω2={t3}；(f)重复第3)- 4)步，得到Ω3={t4}；(g)重复第3)- 4)步，得到Ω4=φ，获得SEC2={t2，t3，t4}.最终{t1，t2，t3，t4}得到的二阶等价类有两个：{t1}和{t2，t3，t4}.

按照规则ψ1，要求t2和t3在Salary属性上的值相同；同样，t3和t4在Salary属性上的值也需相同.因此，虽然DIFF(t2，t4)ω，但也应放在同一个类别中进行比较.

定义6.RwA规则一致性.I是R上的一个实例，A、B是R上的属性，规则ψ∈RwA，ψ关于I是一致的，当且仅当，对于任意元组ti和tj，在ti和tj属于同一个二阶等价类的条件下，若ti[A]=tj[A]，则ti[B]=tj[B]，记作I|=ψ.否则，I关于ψ是不一致的，记作I|≠ψ.

根据定义6，对于例4中的二阶等价类{t2，t3，t4}，当t2[TeaID]=t3[TeaID]，却有t2[Salary] ≠t3[Salary]，元组t2和t3相互冲突，记作：t2⊗t3.同理，t3⊗t4.因此，Accident|≠ψ1.

定义7.RwLE规则一致性.I是R上的一个实例，A、B是R上的属性，规则ψ∈RwLE，ψ关于I是一致的，当且仅当，对于任意元组ti和tj，在ti和tj属于同一个一阶等价类的条件下，有集合Ω={tj|DIFF(ti，tj)～ω}(ti，tj在同一时间区间内)，tj∈Ω，若ti≼Atj，则tiOPBtj，记作I|=ψ.否则，I关于ψ是不一致的，记作I|≠ψ.

根据定义7，表1中t1≼VTt2，但t1[Salary]≥t2[Salary]，违反了ψ2，因此Accident|≠ψ2；同理，t3≼VTt4，但t3[level]≥t4[level]，因此Teacher|≠ψ3.

定义8.RwF规则一致性.I是R上的一个实例，A、B是R上的属性，对于I上任意一条元组ti，规则ψ∈RwF，ψ关于I是一致的，当且仅当，在ti和tj属于同一个一阶等价类的条件下，对于集合Ω={tj|DIFF(ti，tj)～ω}∪ti，若f(Ω(A))≈tpA，则ti[B]≈tpB，记作I|=ψ.否则，I关于ψ是不一致的，记作I|≠ψ.

其中，“≈”表示与条件模板匹配.根据定义8，表1中元组t3，对于规则ψ4，获得集合Ω={t1，t2，t3}，f(Ω(AccidentType))=COUNT(Ω(AccidentType))=3，COUNT(Ω(AccidentType))≈≥3，而t3[Level]≤2，因此，元组t3违反了ψ4，Accident|≠ψ4.

定义9.干净数据.给定关系模式R上的数据实例I以及TDQRs规则集合Σ，对于∀ψi∈Σ，都有I|=ψi，则称I为干净数据.

定义10.ω1≫ω2.“≫”为时间关系运算符，表示ω1和ω2时间上的关系.

假设有ω1表示2 years，ω2表示1 year，易见，若ψ在ω1上成立，则必在ω2上也成立(证明参见2.2小节).如例2中在L1成立的条件下，此时将ω1改为ω2，有L1*：若发生教学事故，且事故类型为A，则1年内，教师编号唯一决定教师工资.易见，L1*也成立.本文将ω1和ω2的这种关系表示为ω1≫ω2.

2.2 TDQRs的性质

关系模式R上所有属性集合为U，Σ是U上一组时态数据质量规则，于是有关系模式R，本小节针对R，给出其上满足的一些性质及证明.

1)若ψi∈RwA(i=1，2，3…n)，则满足如下3条性质.

性质1.若(VT|ω1：X→Y，)，且ω1≫ω2，则(VT|ω2：X→Y，).

证明：反正法.假设(VT|ω2：X→Y，)不成立，由定义6可知，有二阶等价类SECk，存在ti和tj∈SECk，若ti[X]=tj[X]，则ti[Y]≠tj[Y]；又已知ω1≫ω2，DIFF(ti，tj)～ω2，由定义3和定义10易得，DIFF(ti，tj)～ω1，因此在相同的条件模板下，有ω1生成的二阶等价类SECM，使得SECk⊆SECM，且ti和tj∈SECM；又因为ti[X]=tj[X]，有ti[Y]≠tj[Y]，使得(VT|ω1：X→Y，)不成立，与已知条件矛盾.得证.

性质2.若(VT|ω1：X→Y，)，(VT|ω2：Y→Z，)，且ω1≫ω2，则(VT|ω2：X→Z，).

证明：已知(VT|ω1：X→Y，)成立，且ω1≫ω2，由性质1可得，(VT|ω2：X→Y，)成立；由定义6可知，存在一个二阶等价类SECk，对于任意的ti和tj∈SECk，若ti[X]=tj[X]，有ti[Y]=tj[Y]；又因为(VT|ω2：Y→Z，)成立，存在相同的二阶等价类SECk，有ti[Y]=tj[Y]，则ti[Z]=tj[Z]；因此，有相同的二阶等价类SECk，ti和tj∈SECk，若ti[X]=tj[X]，则ti[Z]=tj[Z]，(VT|ω2：X→Z，)成立.得证.

性质3.若(VT|ω1：X→Y，)，且Z⊆U，则(VT|ω1：XZ→YZ，).

证明：已知(VT|ω1：X→Y，)成立，由定义6可知，存在一个二阶等价类SECk，对于任意的ti和tj∈SECk，若ti[X]=tj[X]，有ti[Y]=tj[Y]；又因为在相同的二阶等价类中，已知ti[XZ]=tj[XZ]，易得，ti[X]=tj[X]和ti[Z]=tj[Z]，于是有ti[YZ]=tj[YZ]；因此，(VT|ω1：XZ→YZ，)成立.得证.

2)若ψi∈RwLE(i=1，2，3…n)，则满足如下3条性质.

性质4.若(VT|ω：q1→κ，)，且(VT|ω：q2→κ，)，则(VT|ω：q1∧q2→κ，).

证明：因为(VT|ω：q1→κ，)成立，由定义7可知，存在一个一阶等价类FECk，对于任意的ti和tj∈FECk，若DIFF(ti，tj)～ω，使得q1为TRUE，则有κ；又因为(VT|ω：q2→κ，)成立，使得ti和tj在相同的前提条件下，若q2为TRUE，则有κ，因此易得，q1∧q2也为TRUE时，有κ，因此(VT|ω：q1∧q2→κ，)成立.得证.

性质5.若(VT|ω：ti≼Xtj→ti≼Ytj，)，且(VT|ω：ti≼Ytj→tiOPZtj，)，则(VT|ω：ti≼Xtj→tiOPZtj，).

证明：因为(VT|ω：ti≼Xtj→ti≼Ytj，)成立，由定义7可知，存在一个一阶等价类FECk，对于任意的ti和tj∈FECk，且DIFF(ti，tj)～ω，使得若ti≼Xtj，有ti≼Ytj；同理，因为(VT|ω：ti≼Ytj→tiOPZtj，)成立，在相同的前提条件下，已知ti≼Ytj，则tiOPZtj成立.因此有，对于任意的ti和tj∈FECk，且DIFF(ti，tj)～ω，若ti≼Xtj，则必有tiOPZtj.可得(VT|ω：ti≼Xtj→tiOPZtj，，成立.得证.

性质6.若(VT|ω1：ti≼Xtj→tiOPYtj，)，且ω1≫ω2，则(VT|ω2：ti≼Xtj→tiOPYtj，).

证明：反正法.假设(VT|ω2：ti≼Xtj→tiOPYtj，)不成立，由定义7可知，有一阶等价类FECk，存在ti和tj∈FECk，对于ti，有集合Ω2={tj|DIFF(ti，tj)～ω2}，tj∈Ω2，使得若ti≼xtj，有ti!OPYtj；又已知ω1≫ω2，因为DIFF(ti，tj)～ω2，必有DIFF(ti，tj)～ω1，所以存在集合Ω1={tj|DIFF(ti，tj)～ω1}，且Ω2⊆Ω1，易得ti，tj∈Ω1；又ti≼xtj，则ti!OPYtj，因此，(VT|ω1：ti≼Xtj→tiOPYtj，)不成立，与已知矛盾.得证.

进行不一致数据检测时，TQDRs规则越多，时间开销越大.因此，可以利用以上性质，去除冗余的规则，提升查询效率.例如，假设规则集中包含如下3条规则：

ψ1*：(VT|forever：ti≼VTtj→ti≼Titletj，)

ψ2*：(VT|forever：ti≼Titletj→ti[Salary]≤tj[Salary]，)

ψ3*：(VT|forever：ti≼VTtj→ti[Salary]≤tj[Salary]，)

3 基于TDQRs不一致数据的检测

对于给定的关系模式R上的一个实例I和用于检测不一致数据的TDQRs约束规则集Σ，本节针对RwA、RwLE和RwF这3种子规则分别给出不一致数据的检测算法.

3.1 RwA规则的检测算法

对于RwA规则，本文通过创建一棵冲突检测树的方法获取数据集中不一致数据.冲突检测树深度为4，第0层为根结点，保存要检测的数据集地址；第1层获取一阶等价类的元素作为根结点的一级子结点；第2层获取二阶等价类的元素作为根结点的二级子结点；以第2层结点为父结点，依次遍历，获取每个结点在Y属性上的不同取值，作为第3层结点.检测算法DetectWithRwA如算法1所示.

算法1.DetectWithRwA(I，ψ)

输入：数据实例I，RwA规则ψ

输出：冲突检测树Tree

1. M=Ø；

2. CreateTree()；

3. arrayFirst=GetFirtstEquClass(ψ)；

4. FOREACH e1in arrayFirst DO

5. AddFirstNode()；

6. arraySecond=GetSecondEquClass(e1，ψ)；

7. FOREACH e2in arraySecond DO

8. AddSecondNode()；

9. arrayThird=GetConflictValue(e2)；

10. AddEachNodeInArrayThird()；

11. IF e2.Child.Count>1 THEN

12. M=M∪child；

13. END IF

14. END FOR

15. END FOR

16. RETURN Tree；

算法1中，第3行获取一阶等价类，第6行获取二阶等价类，第7-13行用于判断第2层结点的孩子结点数，若超过1，则冲突，并将孩子结点加入集合M.

算法复杂度，一阶等价类的创建可在O(n)完成、二阶等价类创建可在O(n2)完成，查找冲突元组可在O(n)完成.那么，算法1的时间复杂度为O(n2).

例5.根据算法1，用本文的ψ1规则检测表1，可创建一棵冲突检测树，如图1所示.

图1 冲突检测树Fig.1 Conflicts detect tree

树中的每个结点有3个域，分别用于存储数据、首个孩子结点地址和下一个兄弟结点的地址.一棵冲突检测树有如下结论.

结论1.冲突检测树的深度为4，叶子结点中所包含的元组数为关系R中所有元组的子集.

结论2.叶子结点中，对于数据域的任意两个元组ti和tj，若ti和tj的父结点不同，则必有DIFF(ti，tj)ω.

结论3.叶子结点中，若某个结点存在兄弟结点，则该结点与其兄弟结点包含的元组互为冲突对；若某个结点不存在兄弟结点，则该结点包含的元组不存在冲突.

值得注意的是，可以通过遍历图1中的冲突检测树进行不一致数据的检测.本文采用链表的方式进行不一致数据的存储是因为考虑到数据集中的元组时刻发生变化，而链表存储的方式可以保证在原冲突检测树不变的情况下，方便的添加以及删除结点.为了提升不一致数据的查询效率，在执行检测任务前，可先对冲突检测树剪枝，进行三次优化操作.

首次优化：对叶子结点进行优化操作，由结论3可知，无兄弟结点的叶子结点包含的元组不存在冲突，因此图1中可将包含t1的叶子结点删除；

二次优化：对第2层结点进行优化操作，若第2层的结点无子结点，则该结点包含的元组不会产生冲突，可删除该结点，因此图1中可将包含t1的第2层结点删除；

三次优化：对第1层结点进行优化操作，若第1层的结点无子结点，则该结点包含的元组不会产生冲突，可删除该结点，因此图1中可将包含t5和t6对应的结点删除.

图1的优化过程如图2所示.

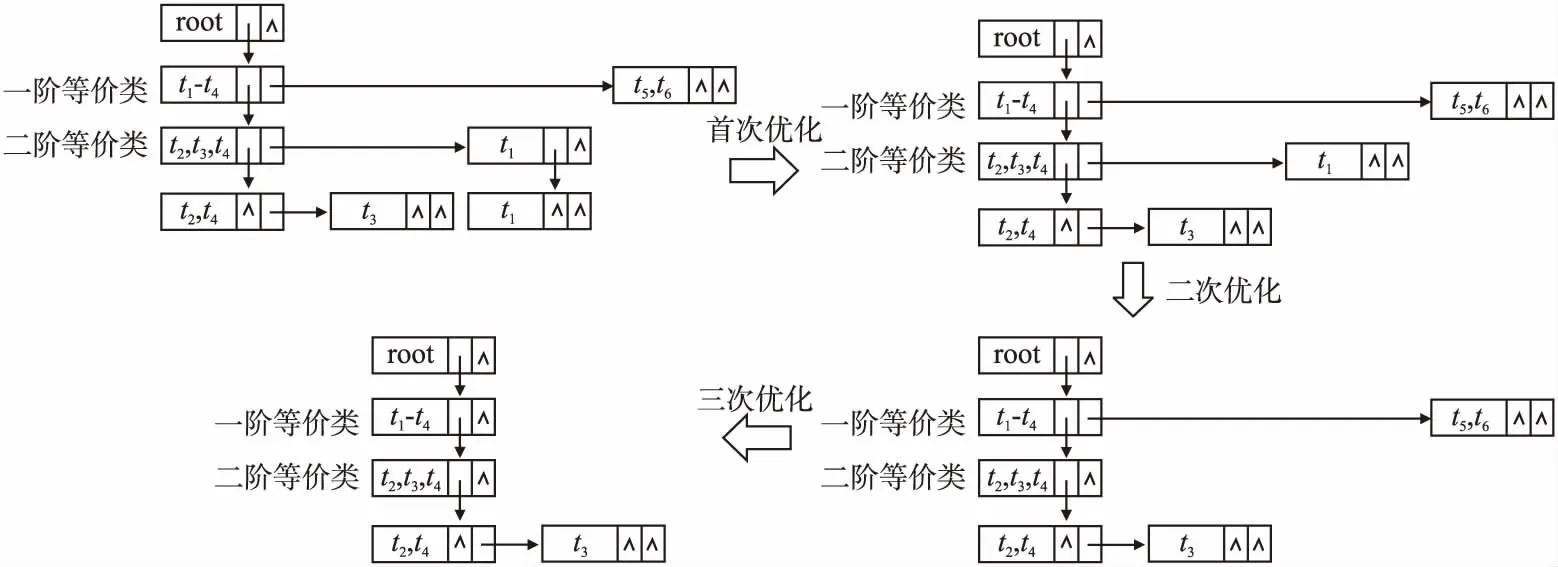
图2 冲突检测树优化过程Fig.2 Optimization process of conflicts detect tree

3.2 RwLE规则的检测算法

对于RwLE规则，首先根据条件模板遍历数据集获得一阶等价类，再根据时序关系判断对应的属性值是否满足偏序条件，若不满足，则将一阶等价类的值放入集合M中.检测算法DetectWithRwLE如算法2所示.

算法2.DetectWithRwLE(I，ψ)

输入：数据实例I，RwLE规则ψ

输出：冲突集合M

1. M=Ø；

2. equClass=GetFirstEquClass(ψ)；

3. FOREACH e in equClass DO

4. Order e by VT ASC

5. FOREACHtiin e

6. FOREACHtjin e

7. IF DIFF(ti,tj)～ωand (ti,tj) violatesψ

8. M.Add(e)；

9. END FOR

10. END FOR

11. END FOR

12. RETURN M；

算法第2行用于获取等价类，第3-7行比较每个等价类中的元组是否按时间满足相应要求，第8行将不满足要求的等价类放入M中.

算法复杂度，一阶等价类的创建可在O(n)完成、查找冲突元组可在O(n2)完成.那么，算法2的时间复杂度为O(n2).

3.3 RwF规则的检测算法

对于RwF规则，首先遍历数据集的每条元组，再根据规则中的X划分一阶等价类，利用一阶等价类和ω获取定义8中的集合Ω，对集合按照用户定义的函数求值，若与模板不匹配，则将相应元组放入集合M中.检测算法DetectWithRwF如算法3所示.

算法3.DetectWithRwF(I，ψ)

输入：数据实例I，RwLE规则ψ

输出：冲突集合M

1. M=Ø；

2. FOREACHtiin I DO

3. equClass=GetFirstEquClass(ψ)；

4. FOREACHtjin equClas DO

5. value=F(tj)；

6. IF(ti，value)violatesψ(tp)

7. M.Add(ti)；

8. END FOR

9. RETURN M；

算法第3行用于获取一阶等价类，第5行对集合Ω按照用户定义函数求值，第6行判断元组ti是否与模板tp匹配，第7行将不匹配的元组加入M.

算法复杂度，一阶等价类的创建可在O(n)完成、查找冲突元组可在O(n2)完成.那么，算法3的时间复杂度为O(n2).

4 查询语言

为查找数据库中存在的不一致数据，本文设计了一种不一致数据查询语言(Inconsistent Data Query Language，简称IDQL语言)，包含CREATE和SELECT两种语句.

1)CREATE语句用于创建冲突检测树，语法如下：

CREATE TREE

FROM

WITH RULE

其中，为冲突检测树名称；为要检测的数据集名称；为RwA的一条规则.

2)SELECT语句用于查询冲突元组，语法如下：

SELECT

FROM

WHERE

[RULE TYPE ]

[WITH RULES ]

[WITH OPTIMIZATION]

其中，为根据数据质量规则或冲突检测树投影出数据集中冲突元组对；为表名或冲突检测树名；为查询条件；为规则类型；[WITH RULES ]为可选项；为RwLE或RwF规则；[WITH OPTIMIZATION]为可选项，表示是否优化查询.

例6.可以使用IDQL语言执行以下语句.

Q1：根据ψ1规则，为Accident表创建冲突检测树，树名为DetectTree.

CREATE TREE DetectTree

FROM Accident

WITH RULE (VT|2years：TeaID→Salary，)

通过Q1执行算法1创建冲突树.

Q2：若发生教学事故，查找TeaID为1-2000的教师在2年内的工资是否一致，若冲突，将冲突元组显示出来.

SELECT M.tuple

FROM DetectTree

WHERE TeaID BETWEEN 1 AND 2000

通过算法1生成的冲突树，查找冲突集合M中满足条件的冲突元组.

Q3：对Q2优化查询(此时先对DetectTree进行剪枝操作，再查询).

SELECT M.tuple

FROM DetectTree

WHERE TeaIDBETWEEN 1AND 2000

WITH OPTIMIZATION

对算法1生成的冲突树进行剪枝操作，再查询.

Q4：找出工资未随VT时间单调增长的教师编号.

SELECT M.tuple

FROM Accident

RULE TYPE RwLE

WITH RULES (VT|forever：ti≼VTtj→ti[Salary]≤tj[Salary]，)

通过Q3执行算法2.

Q5：5年内，若教师的教学事故累计3次，则Level的值小于等于2.

SELECT M.tuple

FROM Accident

RULE TYPE RwF

WITH RULES

(VT|5years：TeaID，COUNT(AccidentType)→Level，<(≥3，≤2)>)

通过Q5执行算法3.

5 实 验

实验数据集为某高校教职员工2010年-2019年共计10年的信息数据，采集信息平台中获奖、教学事故以及教职员工基本信息3方面的数据，实验中，为了方便的在同一数据集上执行不同种类的子规则，故将以上信息融合至一张表，称为Teaher.关系模式Teacher(ID、TeaID、TeaName、TeaAge、TeaSex、Prize、Bonus、Level、Title、AccidentType、Salary、VT、VTType)由13个属性组成，分别表示为元组编号、教师编号、姓名、年龄、性别、获奖名称(允许为空)、奖金、级别、事故类型(允许为空)、工资、事故(获奖)发生时间，事故(获奖)发生时间类型(1为教学事故时间，2为获奖发生时间).数据集中记录了2239位教职员工共计41876条记录.在此数据集上进行实验，来验证基于时态的数据质量规则的检测方法的性能.

5.1 实验设置

实验环境：实验基于Microsoft Windows 10操作系统，开发环境为Microsoft Visual Studio 2013，数据库采用SQL SERVER 2012.为了进行错误检测，向Teacher表注入2.5%-20%的噪声数据.

在Teacher上，有15条TDQRs规则，依据2.2小节的性质，去掉冗余的规则，本文使用剩余8条TDQRs规则检测Teacher上不一致数据.8条TDQRs规则如表2所示.

表2 关系Teacher上的数据质量规则Table 2 TDQRs on Teacher

5.2 覆盖率

对于给定的ψ，将实际违反ψ的单元格集合记为RealErrorψ，|RealErrorψ|为实际违反ψ的单元格数.若几个单元格作为一个冲突对共同违反了ψ，称这几个单元格被规则ψ检测出来，由文本算法依据规则ψ测出的所有单元格集合记为DetectErrorψ，|DetectErrorψ|为算法测得违反ψ的单元格数.如例5中，DetectErrorψ1={{{t2，t4}，t3}}，|DetectErrorψ|=3.这里引入覆盖率的概念以检测本文方法的有效性，如公式(1)所示.

ψ的覆盖率=|DetectErrorψ∩RealErrorψ|/|RealErrorψ|

(1)

类似地，对一个时态数据质量规则集Σ，覆盖率如公式(2)所示.

Σ的覆盖率=|∪ψ∈ΣDetectErrorψ∩RealErrorΣ|/|RealErrorΣ|

(2)

经过8次独立的运行，得到时态数据质量规则(TDQRs)的覆盖率，如图3所示.

图3(a)中，当注入10%的噪声数据时，图形显示了表2中ψ1-ψ8规则对于不同的元组规模与覆盖率之间的关系.易见，利用TDQRs规则检测，不同的元组规模得到的覆盖率均波动不大，体现了算法的稳定性.同时，图形显示通过算法获得的覆盖率值较高，均介于0.9-1之间，说明本文提出的算法在基于时态的数据集中检测冲突元组方面具有较好的性能.

图3 覆盖率Fig.3 Coverage

图3(b)在元组数为2×104时，显示了不同的错误率与覆盖率之间的关系.其中，随着错误率的增高，覆盖率略有下降，这是由于数据集中错误数据增加后，更多的错误数据被分散到不同的实体中，当同一实体只有一条元组或多条元组同为错误时，算法无法检测导致.

5.3 实验性能

图4分别从元组数和错误率两个方面检测TDQRs的3种规则对应算法的性能.向数据集注入10%的噪声，选择ψ6、ψ2和ψ8对应TDQRs的3种规则执行算法1、算法2和算法3,3种规则的时间复杂度均为O(n2)，因此，图4(a)中随着元组数增加，3种规则的运行时间接近，其中RwA的时间开销稍高，是因为算法需要创建二阶等价类耗费了一些代价.图4(b)展示了对于2×104元组的数据集，随着错误率增高，算法的运行时间.图中显示，运行时间并不会随之增长，这是因为算法的时间开销只与元组数相关，不受错误数的影响.

图4 TDQRs运行时间随元组数、错误率的变化Fig.4 Running time of TDQRs with different number of tuples and different error ratio

设置错误率为10%，选择ψ6、ψ2和ψ8这3条规则分别执行算法1、算法2和算法3，将总的耗费代价作为TDQRs的总运行时间，元组规模与总运行时间的关系如图5(a)所示.图5(a)中，每种规则耗费的时间复杂度均为O(n2)，TDQRs的总时间复杂度仍然为O(n2)，因此图形呈现出二次曲线的形状.随着元组规模的增大，TDQRs运行时间也随着增长，但无论元组规模多大，总运行时间均能在多项式时间内完成检测工作.

图5(b)展示了在10%的错误率下，每检测到一个冲突对，花费的平均时间.由图可知，随着元组规模增大，均摊到检测每一个冲突对的时间开销也随之增加，且呈线性增长.这是由于TDQRs总运行时间的复杂度为O(n2)，错误率固定时，算法检测到的冲突对个数与n值基本呈线性关系，且n值越大，检测到的冲突对个数也越多，将总运行时间与冲突对个数相除，获得的单个冲突对的检测时间也符合一次线性函数，且随着n值的增长而递增.

图5(c)展示了当元组数为2×104时，随着错误率的增加，检测单个冲突对花费的平均时间逐渐减少.这是由于规则的总运行时间并不随错误率的增加而发生变动，虽然错误率的增加会使得少部分冲突对难以检测出来，但这部分冲突对的影响甚微，不会改变被检测出的冲突对总个数随错误比率呈线性增长的趋势，两者相除，获得的单个冲突对的检测时间接近于反比例函数关系.故而导致图形随错误率的增加，均摊在检测每个冲突对耗费的代价呈下降趋势.

图5 TDQRs的总运行时间以及检测一个冲突对的平均时间Fig.5 Total running time of TDQRs and average running time of a conflict

RwA规则在创建冲突检测树时可以通过剪枝的方法进行优化查询，图6(a)展示了错误率为10%时RwA规则在优化前和优化后在查询时间上的对比.由图6(a)可知，在执行例6中的Q3查询时，优化后的查询时间明显低于优化前，这是因为优化方法中的3次剪枝操作使得冲突树只保留了不一致的数据，而这部分数据只占数据集的很小比例，遍历时，算法在很短时间内能查询到对应的不一致数据.图6(b)中，数据规模为2×104条元组，时间开销随着错误率的增加缓慢增长，这是由于错误越多，优化后冲突树中保留的结点就越多，遍历时耗费的时间代价就越大.

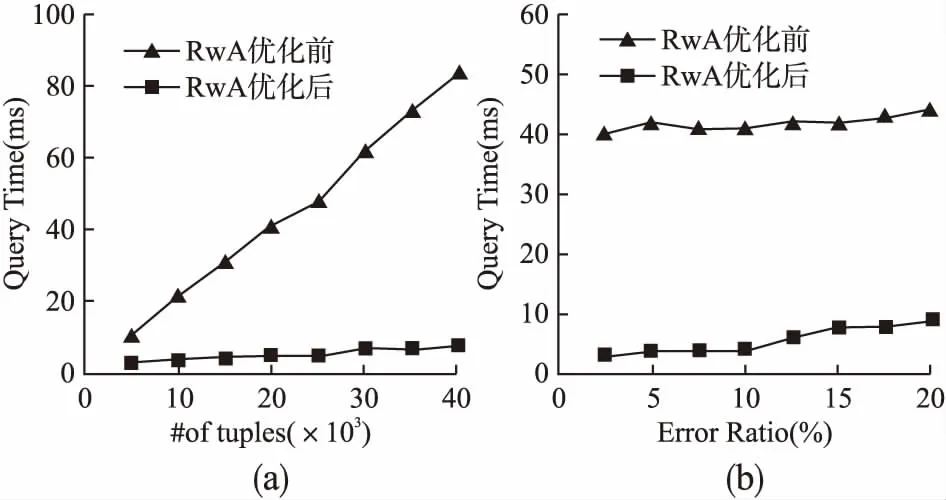
图6 优化技术对运行时间的影响Fig.6 Effect of running time with optimization technology

从上述实验结果可以看出，本文提出的时态数据质量规则检测方法可以有效地检测出时态条件下的不一致数据.且本文在算法1的基础上提出的3次优化操作进行不一致数据查询时，查询效率得到了明显的提高.

6 总 结

本文对已有的函数依赖进行扩展，加入时态语义，提出了时态数据质量规则，并给出了规则相关的性质及对应的检测算法.此外，本文还提出了IDQL语言用于查询不一致数据.最后，通过实验验证了时态数据质量规则能够检测出更多的不一致数据，且算法可在多项式时间内完成.然而，检测出不一致数据后，还需对不一致数据加以分析，获得可靠的修复方案，本文的下一步工作将基于时态数据质量规则，研究不一致数据的修复方法.