邻域感知的不平衡数据集过采样方法
严远亭,戴 涛,张以文,赵 姝,张燕平
(安徽大学 计算机科学与技术学院,合肥 230601)
1 引 言
分类是机器学习的一个重要研究分支[1].经典的分类器大多针对不同类别样本数量相近的情况下进行分类[2].但并非所有的数据集都保持类间和类内平衡.在一个数据集中,当一个类别的样本数量远远多于(或少于)其它类别时,此数据集称为不平衡数据集[3].在不平衡数据集中,少数类样本是重要的研究样本.实际应用中,很多数据集都存在不平衡现象.例如:文本分类[4,5]、欺诈识别[6]、石油勘探[7]、医疗诊断[8-11].这些数据集中的少数类样本往往更具有研究价值.但是,在不平衡的数据中,由于被研究的类别在整个数据集中所占比例较低,少数类样本在分类过程中更容易出现分类错误,且将少数类的样本误分为多数类的代价要往往高于将多数类样本误分为少数类的代价.例如,将正常人误诊为癌症患者,通常只需二次复查便可排除,而将癌症患者误诊为正常人,会使患者错过最佳治疗时机.
当前对不平衡数据学习的研究大致可以分为算法层面和数据集层面的两类方法.基于算法层面的典型方法有代价敏感学习[12-15]和核方法[16-19]等,此类方法将不同的数据赋予不同的研究权重,进而对样本进行分类;数据集层面将不平衡数据集通过算法转换成平衡数据集,从而进行分类.基于数据集层面的方法又可分为过采样和欠采样方法.过采样方法是合成新的少数类样本,从而使少数类样本数量与多数类样本数量一致.而欠采样方法是选择部分具有代表性的多数类样本,从而与少数类样本合并形成平衡数据集.
过采样方法是当前主流的不平衡数据集处理方法,例如,随机过采样方法[3],该方法是通过随机选择一定数量的少数类样本,使少数类样本和多数类样本达到平衡.但是,这种方法容易导致模型过拟合.为克服上述缺点,Nitesh V.Chawla等人在2002年提出SMOTE(Synthetic Minority Over-sampling Technique)方法[20].该方法对少数类样本计算其k近邻,随机选择其中一个近邻样本,通过线性插值生成新样本,以此使少数类和多数类样本在数量上达到平衡.然而,由于SOMTE并未考虑所选的近邻样本的空间分布特征,从而增加了样本间发生重叠的概率.
2005年,Hui Han等提出Borderline-SMOTE方法[21],He等人在2008年提出ADASYN(Adaptive Synthetic Sampling Technique)方法[22].两种方法一定程度上克服了SMOTE方法的不足.Borderline-SMOTE方法针对边界域的少数类样本进行过采样.先计算所选的少数类样本的m近邻,若m个近邻中一半以上是多数类样本,则将该样本放入合成新样本所需的中心样本的DANGER集中.从DANGER集中选择一个样本以及该样本的k个少数类近邻样本中的某些样本,计算偏差,通过SMOTE的线性插值方法合成新的少数类样本.ADASYN根据少数类样本的分布自适应生成新少数类样本.难学习的样本会生成更多的新样本.ADASYN不仅能降低原不平衡数据的不平衡度,而且可以自适应的改变决策边界,将重点放在那些难学习的样本上.但是,由于该算法中生成样本数量受密度分布的影响,当k个近邻样本中全为多数类样本时,密度分布的系数值最大,此时该样本将与k个近邻生成多个新少数类样本,但实际上该样本可能为噪声样本.
Sukarna Barua等人在2014年提出一种基于少数类样本的权重过采样合成新的少数类样本的方法[23].MWMOTE(Majority Weighted Minority Oversampling Technique)从原少数类样本中基于k近邻确定重要和难学习的少数类样本,并给这些少数类样本赋予选择权重,最终根据选择权重从重要和难学习的少数类样本中合成新的少数类样本.该方法可以有效地划分出决策边界,并在决策边界附近确定难学习样本,从而生成新少数类样本.但是,此方法处理过程比较复杂,需要确定的参数比较多,同时,该方法有可能忽略有研究价值但不处于决策边界的少数类样本.
SMOTETomek方法由Batista等人于2003年提出[26].SMOTETomek属于过采样与欠采样的联合方法,该方法结合SMOTE和Tomek links[27],先对少数类样本进行过采样,使数据样本达到平衡.然后结合Tomek links技术,清除多数类和少数类相互纠缠的样本(即噪声样本和边界样本).类似的方法还有SMOTEENN[28],相对于SMOTETomek方法,SMOTEENN会对数据进行深度清洗,清除更多的多数类与少数类纠缠的样本.除此之外,还有很多过采样方法,如:V-SYNTH[29]、OUPS[30]、CCR[31]等.
当前的过采样方法大多以如何挖掘边界样本,并基于边界样本信息进行后续的过采样为主要研究目标.但是,考虑不平衡数据集样本分布十分复杂,很难准确的进行边界样本的挖掘.因此,如何有效地利用样本分布信息实现高效的过采样,仍然是不平衡数据学习的重要挑战.本文受构造性神经网络的启发[32],从样本空间分布的角度出发,提出一种基于少数类样本局部邻域信息的SMOTE过采样方法.该方法通过学习样本邻域信息并利用邻域信息约束过采样过程中样本的合成,将样本约束在少数类的邻域内.同时为了尽可能地挖掘样本的有效邻域并探测噪声样本.本文采用了集成策略来克服随机初始化所造成的邻域挖掘过程的不确定性,提高邻域挖掘范围和噪声样本的识别能力.
本文的后续结构分为4个部分.第2部分介绍并分析SMOTE;第3部分详细介绍本文所提的算法;第4部分给出了本文的实验结果及实验分析;第5部分总结本文并对下一步工作进行了展望.
2 相关工作
2.1 SMOTE
SMOTE是最经典的过采样方法之一,该方法有效地解决随机过采样产生的过拟合问题.SMOTE利用线性插值并结合k近邻算法,合成新的少数类样本,从而使得数据达到平衡.该方法随机选择少数类样本,该样本与其k近邻中的一个样本进行线性插值,得到新样本.算法步骤如下:
1)确定所需合成的少数类样本数量M;
2)利用欧氏距离计算少数类样本xq的k个同类近邻,其中k取5;
3)从k个近邻样本中随机选择一个样本xj,与xq合成新的少数类样本 :
(1)
其中q∈{1,2,…,u},j∈{1,2,…,k},α∈[0,1];
4)如果合成的样本数量达到要求,则算法结束,否则,跳转至步骤2.
如图1所示,假设SMOTE从少数类样本中随机选取样本A,A定义为种子样本,利用KNN找到A的5个近邻样本,选择其中的一个近邻样本B,那么样本x1就是利用公式(1)得到的一个合成样本.

图1 SMOTE合成样本示意图Fig.1 Sketch map of SMOTE
2.2 SMOTE算法分析
由于SMOTE利用线性插值合成新的少数类样本,该过程具有随机性.从公式(1)可知,合成样本的位置与种子样本之间的位置关系以及线性插值中的随机变量密切相关.
如图2 (a),当种子样本A与其最近邻样本B处于同一区域的时候,此时进行样本的合成并不会带来噪声,只可能产生少数类样本的重叠现象;另一方面,如图2 (b)所示,假设SMOTE算法中k近邻取值为5,当以C为种子样本时,样本B为其近邻样本之一,以样本C和B进行样本合成时,由于

图2 SMOTE合成样本过程的分析示意图Fig.2 Analysis of the synthetic process of SMOTE
这两个样本不处于同一区域,此时合成的样本x2可能会落入多数类区域内,从而引入了新的噪声样本.同时,有可能产生样本重叠现象(如样本x3),从而影响后续分类模型性能.
3 本文方法
SMOTE的随机性可能增加新噪声样本和重叠样本.为了提升不平衡数据过采样的有效性,本文考虑利用样本的邻域信息,将过采样过程中的合成样本约束在少数类样本邻域内,从而避免引入额外的噪声和异类重叠样本.
构造性神经网络[33]与传统神经网络的不同之处在于,它能够构造性的完成网络模型的自动确定,而不需要预先对网络结构参数进行设定.文献[34]给出了M-P神经元结点的几何意义,即:利用三层神经网络来构造分类器等同于寻找能够划分不同类型的输入向量的邻域集合.构造性神经网络中以超球体作为样本的邻域,每一个超球体都是一个局部模式的学习函数.
借鉴上述构造性神经网络中局部模式的学习方法,本文提出一种针对少数类样本邻域的学习方法.如图3所示,假设图中圆形区域表示学习的少数类样本邻域.通过挖掘少数类样本的局部邻域信息,假设邻域中心为A、B、C、D、E.如图3所示,假设种子样本为C,对C与其近邻样本B使用线性插值并控制合成样本的位置,使其落入少数类局部邻域内,如样本x4落在以C为中心的邻域内.此外,合成的样本也可落入以B或D为中心的邻域中,如样本x5和x6.本文方法控制样本合成的位置,使得新样本既不会与多数类样本发生重叠,也不会成为噪声样本,即不会产生图中样本x7的情况.

图3 邻域信息与SMOTE结合示意图Fig.3 Combing SMOTE and neighborhood information
3.1 邻域信息挖掘
如何有效地挖掘少数类样本的邻域,以便更好地约束样本的过采样过程十分重要.本文受构造性神经网络的启发,提出样本邻域挖掘方法.
假设训练集为D,记少数类样本集为Dm,多数类样本集为Dn.
首先,从Dm中随机选择样本xi,作为邻域中心.利用欧式距离计算离xi最近的异类样本的距离,记为d1.
(2)
其中m∈{1,2,…,p}.
以d1为约束,计算以xi为中心,d1为半径的邻域范围内同类样本与xi的最远距离,记为d2.
(3)
其中m∈{1,2,…,p}.
通过上述过程,本文能够得到一个以xi为邻域中心,θi为半径的少数类样本邻域,本文采取折中[32,35]的办法得到其半径:
θi=(d1(i)+d2(i))/2
(4)
通过标记落在邻域中的样本,能够得到一个少数类样本邻域.重复上述学习过程,直到数据集中的所有样本均被标记为止,此时学习任务结束,获得少数类样本邻域集合{N1,N2,…,Nn}.
3.2 邻域融合
由于邻域信息的挖掘过程带有随机性,所以不同的初始化对应的邻域信息挖掘会有所差异,如图4(a)-图4(c)所示,其中圆形区域表示的是对应的邻域.以图4 (a)和图4 (b)为例,在图4 (a)中,一次邻域信息挖掘后,得到以A、C、D、E、F为邻域中心的样本邻域.此时,以A为中心的邻域包含样本G,以C为中心的邻域包含样本H,以D为中心的邻域包含样本I,以F为中心的邻域包含样本B,以E为中心的邻域为单样本邻域.图4 (b)给出的是另一次邻域信息挖掘后得到的以B、D、E、G、H为邻域中心的样本邻域.此时,样本F被划分到以G为中心的样本邻域里,样本B形成单样本邻域.所以,不同的中心样本选择产生的样本邻域存在一定的差异.本文中,为避免随机初始化造成的不确定性,本文利用集成策略,以尽可能地学习少数类样本的邻域范围.
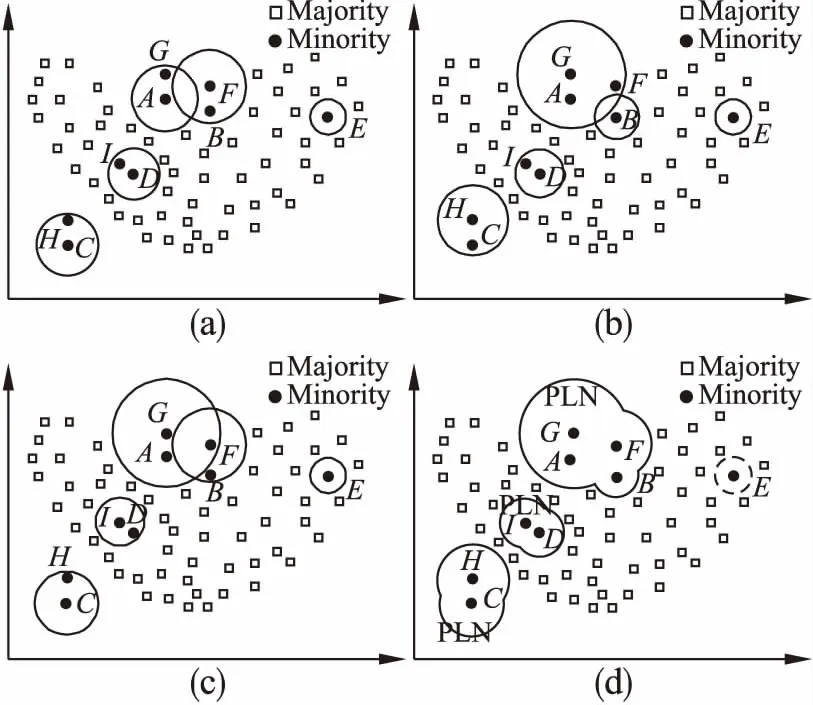
图4 邻域感知过程示意图.(a),(b),(c)分别表示第1,2,3次邻域信息挖掘结果,(d)表示三次挖掘的邻域信息融合结果Fig.4 Sketch map of the proposed neighborhood-aware process.Sub figures(a),(b)and(c)represent the first,second and third times of neighborhood mining results respectively,and(d)denote the combining result of the three results
本文对样本进行多次邻域信息挖掘,每一次形成的邻域都不尽相同.其中一次信息挖掘所形成的少数类样本邻域如公式(5)所示.
(5)

定义少数类样本所在局部邻域为PLN(Positive Local Neighborhood),如公式(6)所示.
PLN=∪Nl
(6)
样本邻域的中心X=∪Xl,半径Θ=∪Θl.该邻域是合成新少数类样本的安全域.在合成新样本时,严格控制新样本的空间位置,使得新合成的样本仅落入PLN中,从而有效避免噪声样本的产生.
3.3 噪声样本检测
SMOTE的随机性增加了产生新噪声样本和样本间发生重叠的可能性.本文提出的方法控制合成的新少数类样本落入PLN中,有效地避免了新噪声样本的产生.但是,当种子样本中有噪声样本时,上述控制合成样本的过程无法有效识别噪声样本,从而使得新合成的样本落入到噪声样本的邻域.为此,本文提出如下的策略检测噪声样本,对样本xi,假设邻域信息挖掘次数为W,那么,若W次邻域挖掘过程都满足公式(7),则定义该样本为噪声样本.
(7)

由公式(7)可知,对于任意一个少数类样本xi,如果在W次的邻域信息学习过程中,该样本所处的邻域中都仅包含该样本,那么该样本所处的邻域则被视为噪声域,该噪声域会被排除在局部邻域的形成过程之外.从而避免噪声样本附近合成新的少数类样本.如公式(8)所示.
x={xi|(xi∈PLN)∧(xi∉NOISE)}
(8)
其中x为合成的样本集.
如图5所示,假设E为噪声样本,选择E与其近邻样本B合成新样本x8,该样本落在以B为中心的邻域内,并不会落入E的附近.该方法可以有效地避免新噪声样本的引入.

图5 噪声域的处理示意图Fig.5 Schematic of noise domain processing
本文的方法通过融合多次邻域信息的挖掘过程,得到最终的少数类样本邻域,在此过程中判断出高概率的噪声样本,利用邻域信息约束后续的样本合成过程,最终得到平衡数据.算法的具体步骤如下:
算法1.邻域感知的过采样技术(NA-SMOTE)
输入:训练集D,训练次数W;
输出:平衡数据集.
步骤:
1.数据预处理,得到少数类训练集Dm,少数类样本数Nm,多数类训 练集Dn,多数类样本数Nn;
2.FORl← 0 toW:
3.FORANYxi∈D:
4. 计算邻域半径θi/*公式(2)~公式(4)*/;
5.Ni=(xi,θi);
6.ENDFOR
8.ENDFOR
9.PLN=∪Nl,X=∪Xl,Θ=∪Θl;
10.WHILEDm′∪Dm 11.FORRANDOMxq∈Dm: 12. 计算xq的k近邻样本,存入distk中; 13.FORRANDOMxj∈distk: 17.ELSE: 18.j- = 1; 19.ENDIF 20.ENDFOR 21.ENDFOR 22.ENDWHILE 23.D′←Dm′∪Dm∪Dn; 24. 输出平衡数据集. 假设用ND表示总样本数,Nn和Nm分别表示多数类和少数类样本数量,f表示特征数量.NA-SMOTE的算法复杂度分析可以分为两步: 1)分析少数类邻域的复杂度:本文算法在一次迭代中进行多次邻域信息挖掘,因此,所获取的任意两个少数类邻域的复杂度有所不同.在最佳的情况下,所有少数类样本都包含在一个少数类邻域中,此时需要计算ND-1个距离,每次计算的复杂度为O(f),因此,总复杂度等于O((ND-1)f).最坏的情况下,每一个少数类邻域仅包含一个少数类样本,此时有Nm个少数类邻域.在这种情况下,少数类邻域的复杂度包含Nm次信息挖掘.对于第一个少数类邻域,其复杂度等于O((ND-1)f),类似的,对于第i个少数类邻域,其复杂度等于O((ND-i)f),对于最后一个少数类邻域,其复杂度等于O((ND-Nm)f).它们构成一个等差数列,因此一次邻域信息挖掘的复杂度为O((2ND-Nm-1)fNm/2),若局部邻域信息挖掘重复W次.其复杂度为WO((2ND-Nm-1)fNm/2), 故挖掘PLN的渐进复杂度为WO(NDNmf). 2)分析基于PLN的过采样复杂度:为使数据集平衡,需要合成Nn-Nm个少数类样本.经典的SMOTE 过采样方法通过选择种子样本并进行线性插值,使不平衡数据集达到平衡.本文仍然采用这一思路,以少数类邻域信息为约束,控制合成 1https://sci2s.ugr.es/keel/imbalanced.php 2https://archive.ics.uci.edu/ml/index.php 本小节介绍了实验所使用的数据集、用以评估实验结果的评价指标以及所使用的分类器;并分析了集成次数与性能的关系、噪声数据探测的结果以及对比实验的结果.实验环境为AMD锐龙2700X(8核16线程、主频3.7GHz)、24GB DDR4 RAM,编程语言为Python(Pycharm1.4). 本文的实验中数据集来自KEEL1和UCI2,其中KEEL数据集样本容量从108到2935不等,不平衡率在1.8到100.2之间.表1给出了KEEL数据集的具体信息.UCI数据集样本容量4873到45211不等,不平衡率在7.5到113.1之间.表2给出了UCI数据集的具体信息.部分数据集根据选择作为少数类的标签属性的不同可以作为不同数据集使用,它们样本容量相同,少数类样本数量和不平衡率不同.其中,Abbr、Ins、Fea、Min、Maj、IR分别表示数据集简写名称、样本容量、样本特征数、少数类样本、多数类样本以及不平衡率. 表1 KEEL数据集详细信息Table 1 KEEL dataset details 表2 UCI数据集详细信息Table 2 UCI dataset details 本文以处理二分类问题为主要研究对象,将少数类视为正例,多数类视为负例.在实验中根据真实类别和分类器预测类别,可以组合成真正例TP(true positive)、假正例FP(false positive)、真负例TN(true negative)、假负例FN(false negative)4种类型.其混淆矩阵如表3所示. 表3 混淆矩阵Table 3 Confusion matrix 基于混淆矩阵可以得到Accuracy、Precision、Recall、F_measure、G_mean、AUC等常用的性能评价指标. Accuracy作为最常见的评价指标之一,通常来说,正确率越高,分类器性能越好.但是有时候准确率高并不能代表一个算法好.在不平衡数据中,需要研究的样本数量在整个数据集中往往只占很小的比例,在这种样本数量不平衡的情况下,Accuracy指标有很大的缺陷,会错误评估误分类的代价[36,37].Precision在不平衡数据的研究中可能会出现分母为零的情况,因为分类过程中,可能出现将所有的少数类样本误分为多数类样本的情况[37,38].因此,通常采用Recall、F_measure、G_mean、AUC作为不平衡数据分类效果的评价指标. (9) (10) (11) (12) 其中tprate=tp/(tp+fn),fprate=fp/(fp+tn). 当前对不平衡数据的研究中,常用的分类器有SVM、Neural network、Naïve Bayes等等,根据文献[36]的统计,SVM是使用频率最高的分类器,本文也选择SVM作为基分类器. 本节对邻域信息挖掘次数与最终的分类性能的关系进行了研究.为简便起见,本文列出了其中4个典型数据集(glass9、wineqr、yeast11、krk1)上的实验结果.分别对每组实验重复10次并取其均值. 图6给出了邻域信息挖掘次数与算法最终性能之间的关系,其中的邻域信息挖掘次数分别为1、2、5、10、15、20.以图6(a)的Recall指标为例,Recall在W=5时明显升高,随着W的进一步增加,Recall值虽然仍然能够有一些增长,但是提升并不明显,整体上算法性能趋于稳定.考虑到W=20的时候,邻域信息挖掘所耗费的时间大约为W=5时的4倍,但是性能的提升却很小.可以在另外3个数据集上也发现类似的现象.同时,注意到在数据集wineqr上,邻域挖掘次数为10的时候算法性能提升较明显,随着次数的增加,性能逐步稳定.综合考虑分类性能与算法计算复杂度,简便起见,本文选择10为最终的邻域信息挖掘次数. 图6 算法性能与集成次数的关系示意图Fig.6 Influence of independent ensemble number on algorithm performanc 表4给出了本文算法在KEEL数据集上的实验过程中探测出可能是噪声样本的个数.其中Numori表示原始数据中探测的噪声样本数量,Numfol表示训练集中的噪声数量.从表4中可以看出,训练集中的噪声数量大部分多于原始数据集,当本文对样本进行划分训练集和测试集时会稀疏原数据集的少数类样本,使原始数据中处于多数类附近的多个少数类样本稀疏至单个样本,从而增加了该样本被误判为噪声样本的概率. 表4 KEEL数据集对应的少数类噪声样本数量Table 4 Number of noise samples corresponding to KEEL datasets 从表5中可以看出,训练集中噪声的产生与划分数据集的选择有关,使得原始数据集中的正常少数类样本被误分为噪声样本.同时,在5折交叉中也出现了某一次或多次训练集中噪声样本数量为0的情况,说明在某次划分数据集时,并未使原数据集中的正常少数类样本孤立.为了避免这种由交叉验证过程中产生的样本分布的变化,本文方法并不删除测试集上探测出的可能的噪声样本,而是在过采样时避免在此类可能的噪声样本形成的邻域附近合成少数类样本,从而达到避免引入新的噪声样本的可能. 表5 五折交叉训练中噪声样本数量Table 5 Number of noise samples corresponding to training sets in 5-fold cross-validation 本文选择5个过采样方法Random Over Sampling[3]、SMOTE[20]、BorderlineSMOTE[21]、ADASYN[22]和MWMOTE[23],以及两种混合采样方法SMOTETomek[26]、SMOTEENN[28]、CCR[31].在对比实验中,分别用缩写ROS、SMO、B-SMO、ADAS、MWMO、SMO-T、SMO-E、CCR代替上述8个算法,用NA-SMO代替本文的NA-SMOTE.实验中,利用SMOTE合成样本时,其最近邻个数均采用SMOTE算法中的默认值,即k=5. DatasetROSSMOB-SMOADASMWMOSMO-TSMO-ECCRNA-SMOglass10.7079±0.01090.7167±0.00850.6957±0.01680.7025±0.01230.7176±0.00610.7088±0.00930.7138±0.01230.6981±0.00000.7172±0.0059wiscon0.9716±0.00140.9730±0.00170.9740±0.00070.9751±0.00090.9732±0.00190.9723±0.00140.9749±0.00180.9718±0.00000.9731±0.0006glass20.7990±0.00800.7971±0.00730.8042±0.00140.7998±0.00200.7990±0.00770.7989±0.00440.7867±0.00430.8065±0.00000.7908±0.0017yeast10.7183±0.00390.7196±0.00280.7396±0.00410.7443±0.00260.7249±0.00230.7190±0.00270.7461±0.00290.7252±0.00000.7231±0.0023nthyd10.9788±0.00420.9801±0.00510.9862±0.0044.9793±0.00750.9785±0.00580.9786±0.00110.9746±0.00660.9737±0.00000.9767±0.0015nthyd20.9829±0.00840.9868±0.00690.9804±0.00160.9783±0.00140.9798±0.00500.9871±0.00580.9831±0.00620.9664±0.00000.9908±0.0061segmt00.9931±0.00040.9921±0.00000.9866±0.00020.9867±0.00010.9933±0.00010.9919±0.00050.9921±0.00040.9926±0.00000.9918±0.0000glass30.8800±0.00800.8837±0.00180.8812±0.00110.8798±0.00200.8842±0.00220.8833±0.00100.8809±0.00670.8826±0.00000.8826±0.0000ecoli10.8929±0.00500.8849±0.01030.9049±0.00740.8886±0.00470.8883±0.01230.8863±0.01290.8870±0.00570.8982±0.00000.8895±0.0018ecoli20.8893±0.00070.8947±0.00110.8657±0.00000.8884±0.00270.8895±0.00900.8942±0.00120.8893±0.00900.8891±0.00000.8909±0.0014ecoli30.8950±0.01130.8766±0.01660.8347±0.00150.8130±0.00940.8222±0.01830.8829±0.01060.8738±0.01920.9237±0.00000.9202±0.0060ecoli40.8853±0.00000.8855±0.00080.8612±0.00000.8811±0.00200.8880±0.00210.8855±0.00060.8873±0.00280.8853±0.00000.8863±0.0010yeast20.6831±0.01500.6823±0.00720.6831±0.01470.6661±0.01280.6744±0.01240.6794±0.00930.7042±0.01100.6830±0.00000.7183±0.0102yeast30.7239±0.00990.7310±0.01260.6785±0.00930.6674±0.00750.7080±0.00860.7290±0.01170.6981±0.00430.7269±0.00000.7535±0.0024yeast40.8938±0.00200.8927±0.00470.8542±0.00530.8618±0.00430.8947±0.00350.8956±0.00350.8982±0.00340.9095±0.00000.9047±0.0020ecoli50.8834±0.00090.8825±0.00800.8684±0.00000.8790±0.00850.8874±0.00280.8828±0.00890.8734±0.01150.8849±0.00000.8780±0.0006ecoli60.8852±0.01730.8664±0.01140.8353±0.00100.8152±0.01320.8231±0.01700.8710±0.01390.8705±0.01640.9436±0.00000.9106±0.0111ecoli70.8769±0.00080.8858±0.00200.8636±0.00000.8741±0.00120.8867±0.00590.8856±0.00110.8773±0.00260.8765±0.00000.8794±0.0014ecoli80.8615±0.00920.8687±0.00600.8693±0.00100.8413±0.00210.8629±0.00860.8709±0.00420.8576±0.00780.8518±0.00000.8639±0.0041 yeast50.7609±0.01420.7561±0.00790.7401±0.00880.7536±0.01270.7523±0.00770.7515±0.01010.7601±0.01270.7727±0.00000.7524±0.0063vowel00.9423±0.00030.9435±0.00040.8992±0.00000.9489±0.00030.9426±0.00040.9434±0.00030.9418±0.00070.9359±0.00000.9467±0.0022ecoli90.8263±0.00520.8425±0.01620.8431±0.00070.8306±0.01630.8370±0.00240.8406±0.01480.8393±0.01550.8567±0.00000.8808±0.0116glass50.7218±0.02430.6928±0.01780.6895±0.01840.7090±0.01040.6409±0.01930.7204±0.02070.7007±0.02990.6645±0.00000.6941±0.0034glass60.9050±0.06000.8454±0.09830.7250±0.00000.9250±0.00000.7250±0.00000.8854±0.08020.9250±0.00000.9250±0.00000.9608±0.0327glass70.7205±0.00630.7197±0.03420.6911±0.01310.7397±0.02220.6588±0.02510.7327±0.02710.7121±0.03200.7206±0.00000.7136±0.0090glass80.7327±0.01440.7229±0.02260.5831±0.00410.7387±0.02280.5946±0.00990.7222±0.02250.7262±0.02710.7253±0.00000.7216±0.0027ecoli100.8677±0.00480.8797±0.00630.8612±0.00050.8613±0.00190.8830±0.00280.8807±0.00250.8709±0.00470.8657±0.00000.8760±0.0011ecoli110.8945±0.00220.8931±0.01160.8743±0.00000.8668±0.00090.8905±0.01450.8967±0.00160.8926±0.00190.8924±0.00000.8923±0.0013yeast60.7452±0.01320.7410±0.01310.7157±0.02100.7429±0.01770.7166±0.02290.7383±0.01420.7435±0.01460.7506±0.00000.7430±0.0013glass90.8944±0.00000.8963±0.00150.8625±0.00190.8963±0.00180.8028±0.00090.8966±0.00190.8779±0.02380.8804±0.00000.9110±0.0171pageb00.9631±0.00100.9495±0.00060.9446±0.00030.9729±0.00150.9145±0.04190.9499±0.00120.9495±0.00090.9564±0.00000.9528±0.0054abalone00.7476±0.01130.7506±0.01730.6043±0.00960.7490±0.00840.6746±0.02200.7397±0.01390.7743±0.01550.7144±0.00000.7629±0.0120dermat1.000±0.00001.000±0.00001.000±0.00001.000±0.0000/1.000±0.00001.000±0.00001.000±0.00001.000±0.0000 续表 图7给出了各个算法在所有数据集上的均值,可以看出,NA-SMO方法整体上要优于其他对比方法.表6给出了各个算法分别在KEEL数据集上10次实验的F_measure均值及对应的标准差,其余3个评价指标见本文附件.由表6可以看出,本文的方法在19个数据集上取得最佳效果.在Recall、G-mean和AUC 上分别在39、19和19个数据集上达到最佳效果(具体结果见附件).表7给出了各个算法在UCI数据集上10次实验的Recall、F_measure、G_mean、AUC均值及对应的标准差.其中,MWMO算法在计算多个UCI数据集时出现内存不足现象,导致无法得出结果.从表7可以看出,本文的方法也取得较好的效果(Recall:4/6、F_measure:5/6、G_mean:5/6、AUC:5/6). 图7 算法性能及其标准差Fig.7 Algorithm performance and the standard deviation 表7 算法在UCI数据集上的结果Table 7 Comparison results on UCI datasets 为进一步对比算法的性能,本文将8个对比算法分别与NA-SMO进行了Wilcoxon Signed Rank Test(威尔科克森符号秩检验),显著性水平选取0.05.表8给出了keel数据集上的检验结果,由于在UCI数据集上,存在部分方法没有得到实验结果,因此无法符号秩和检验.如表8所示,从检验结果来看,本文的算法在绝大多数(26/28)的对比中都与对比算法有显著的差异.结合前文的详细性能对比结果可知,本文的方法与对比算法相比,具有一定的优势. 表8 Wilcoxon Signed Rank Test的结果Table 8 Result of Wilcoxon Signed Rank Test 为进一步详细说明Wilcoxon Signed Rank Test的结果[39],本文选择25个数据集在Recall指标上进行了Wilcoxon T值检验,结果如表9所示.以其中一个T值为例进行分析,例如, ROS有4个数据集的效果好于NA-SMO,但NA-SMO有21个好于ROS,将正Rank累加后得值299,负Rank累加后取绝对值得值26,得到T值为最小值26,由威尔科克森符号秩检验T值临界值表可得,在显著性水平为0.05时25个数据集上T的临界值为89,当T值低于或等于该临界值时拒绝零假设,因此,NA-SMO在此25个数据集上的效果好于ROS. 表9 Wilcoxon T值检验对比结果Table 9 Result of Wilcoxon T test 不平衡数据学习近年来成为机器学习领域中的一个研究热点.SMOTE作为不平衡数据学习中最为经典的过采样方法之一,得到了广泛的研究和应用.但该方法还存在着诸如近邻选择具有一定盲目性、线性插值可能引入额外噪声样本以及产生重叠样本等问题,不少研究针对上述问题提出了一系列的改进算法.但很多改进方法并未考虑到样本空间分布的特性.本文从样本空间分布出发,提出了通过学习样本邻域,并利用邻域信息约束过采样过程中样本合成的范围并实现噪声样本检测,从而尽可能避免噪声样本的产生以及不同类别样本间发生重叠的可能性. 本文在55个KEEL数据集和6个UCI数据集上通过与8个算法的对比验证了邻域信息在不平衡数据学习中的有效性.未来的工作将从两个方面展开,一是研究本文算法的加速方法;另一方面,将研究如何将邻域信息应用到不平衡数据的欠采样中,结合邻域感知的思想进行不平衡数据的欠采样学习.3.4 算法复杂度分析
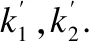
4 实验及分析
4.1 数据集


4.2 评价指标

4.3 分类器
4.4 集成次数性能的关系

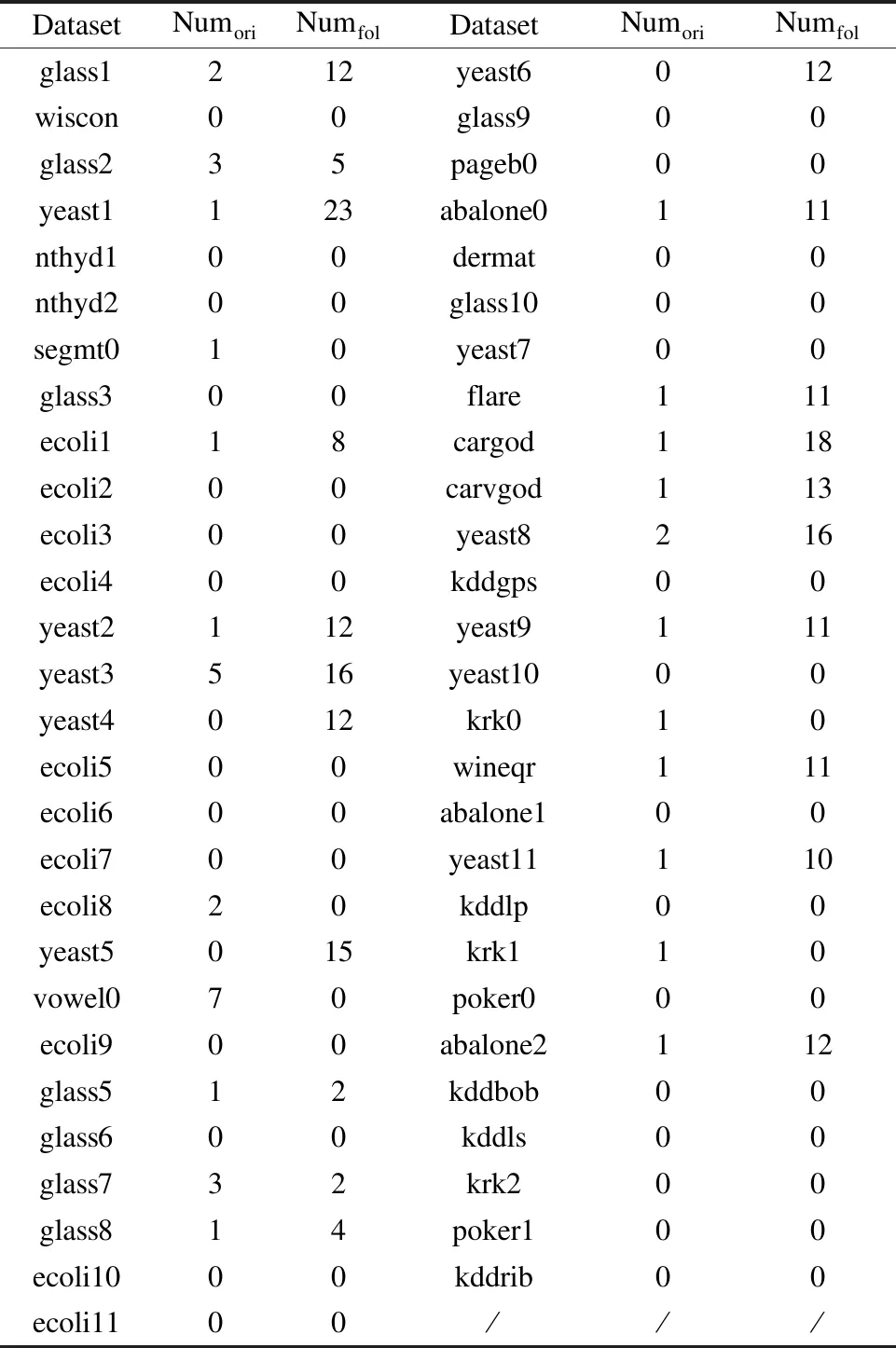
4.5 噪声数据探测

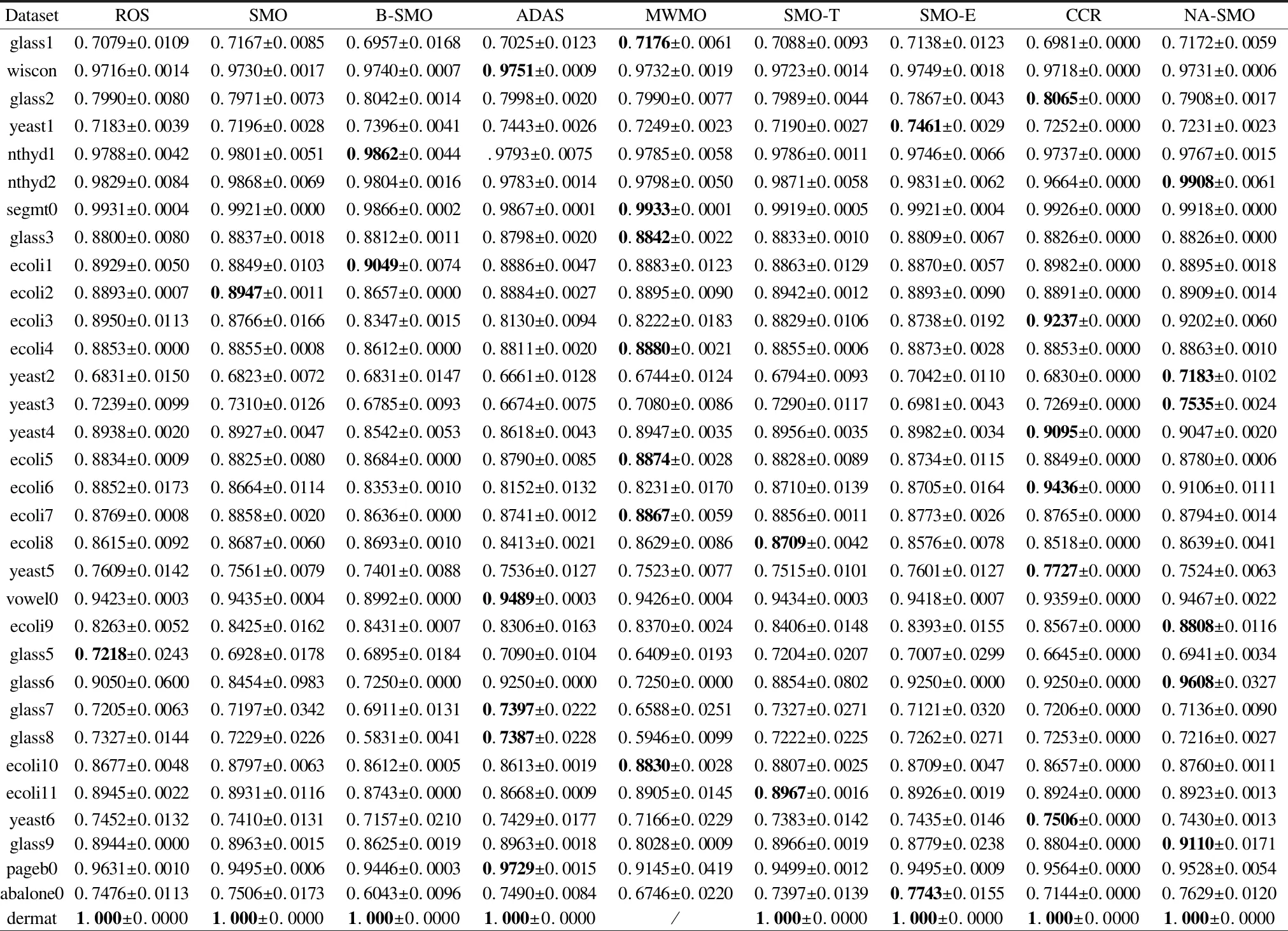
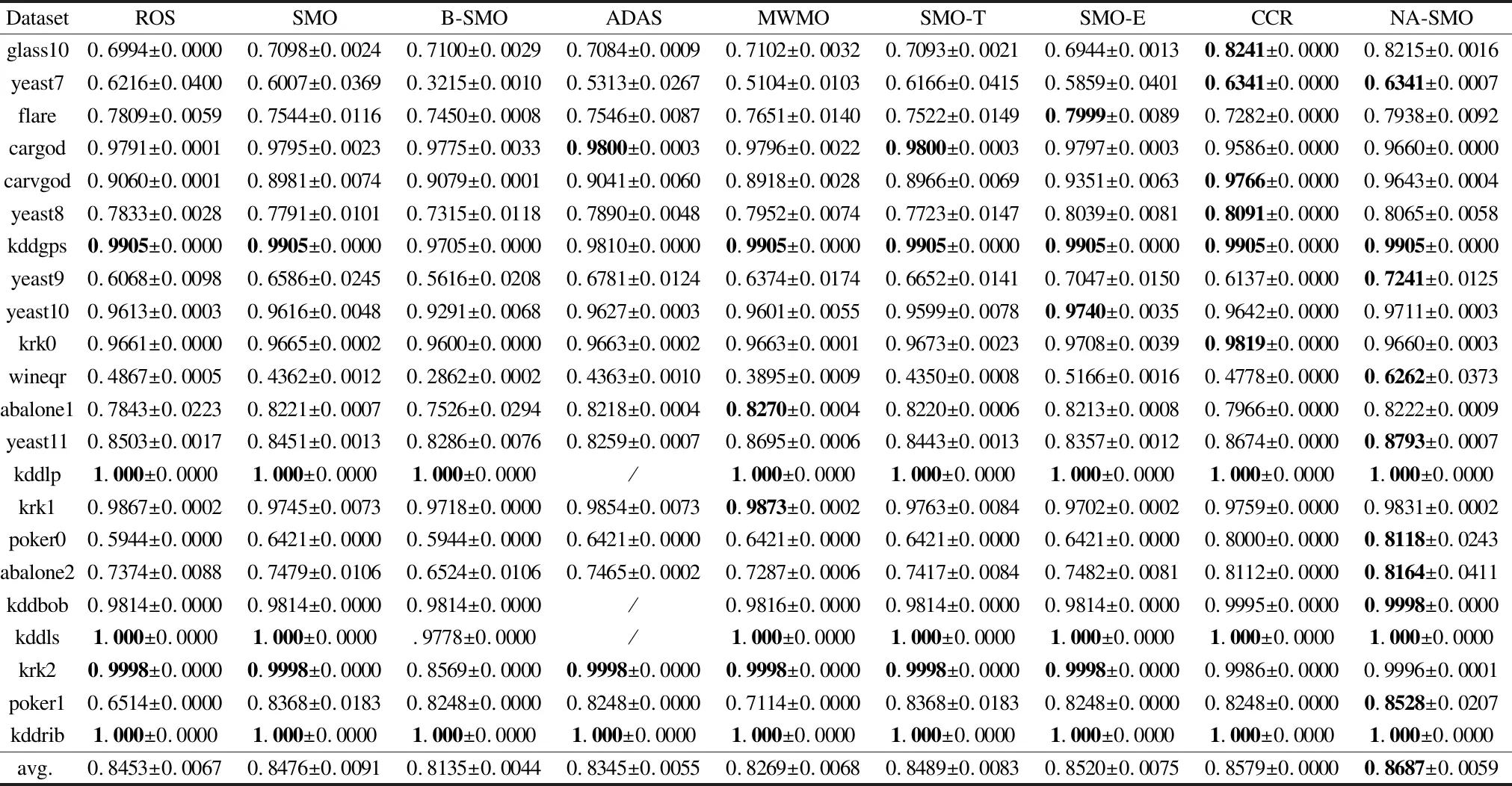
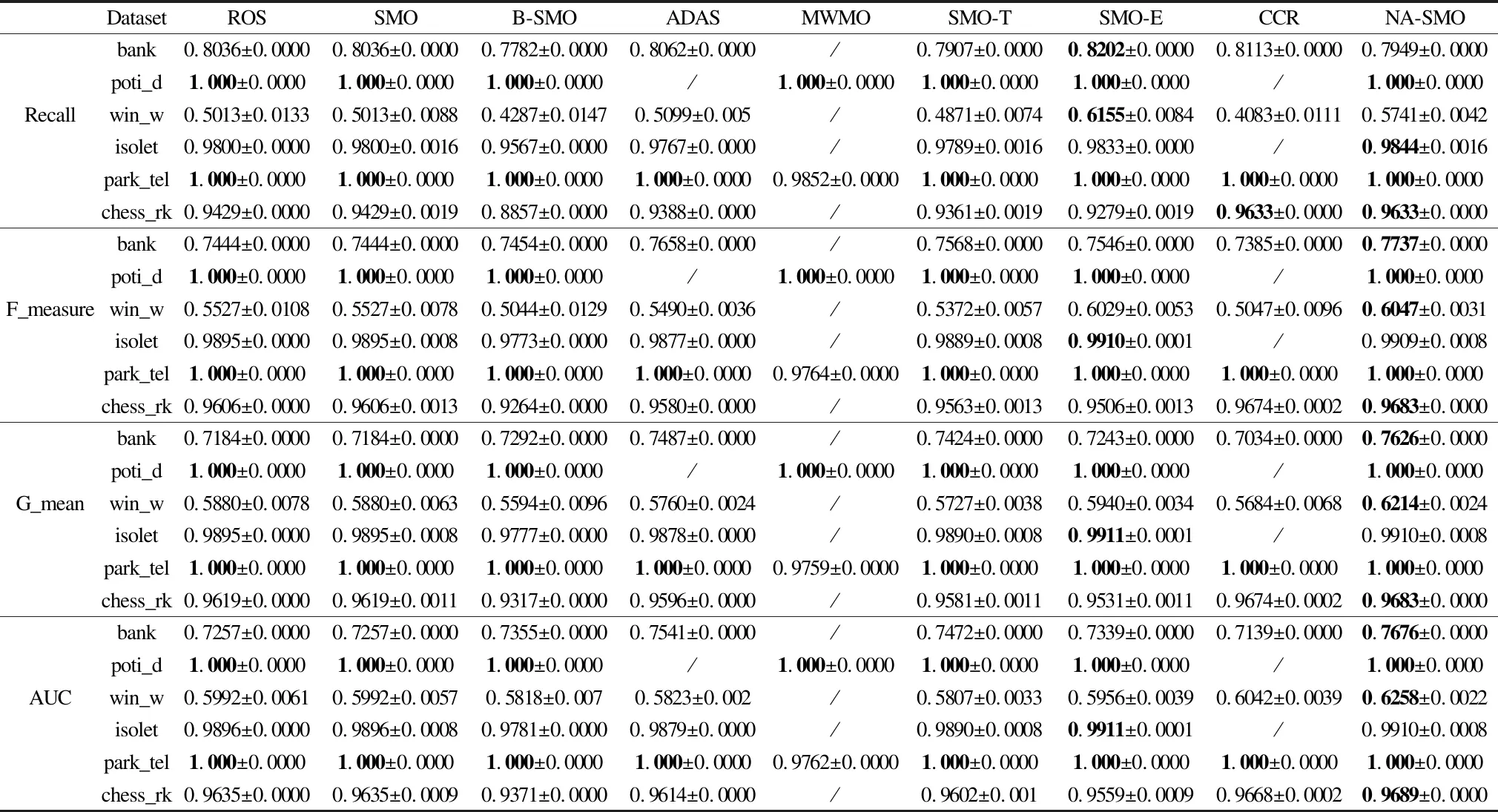
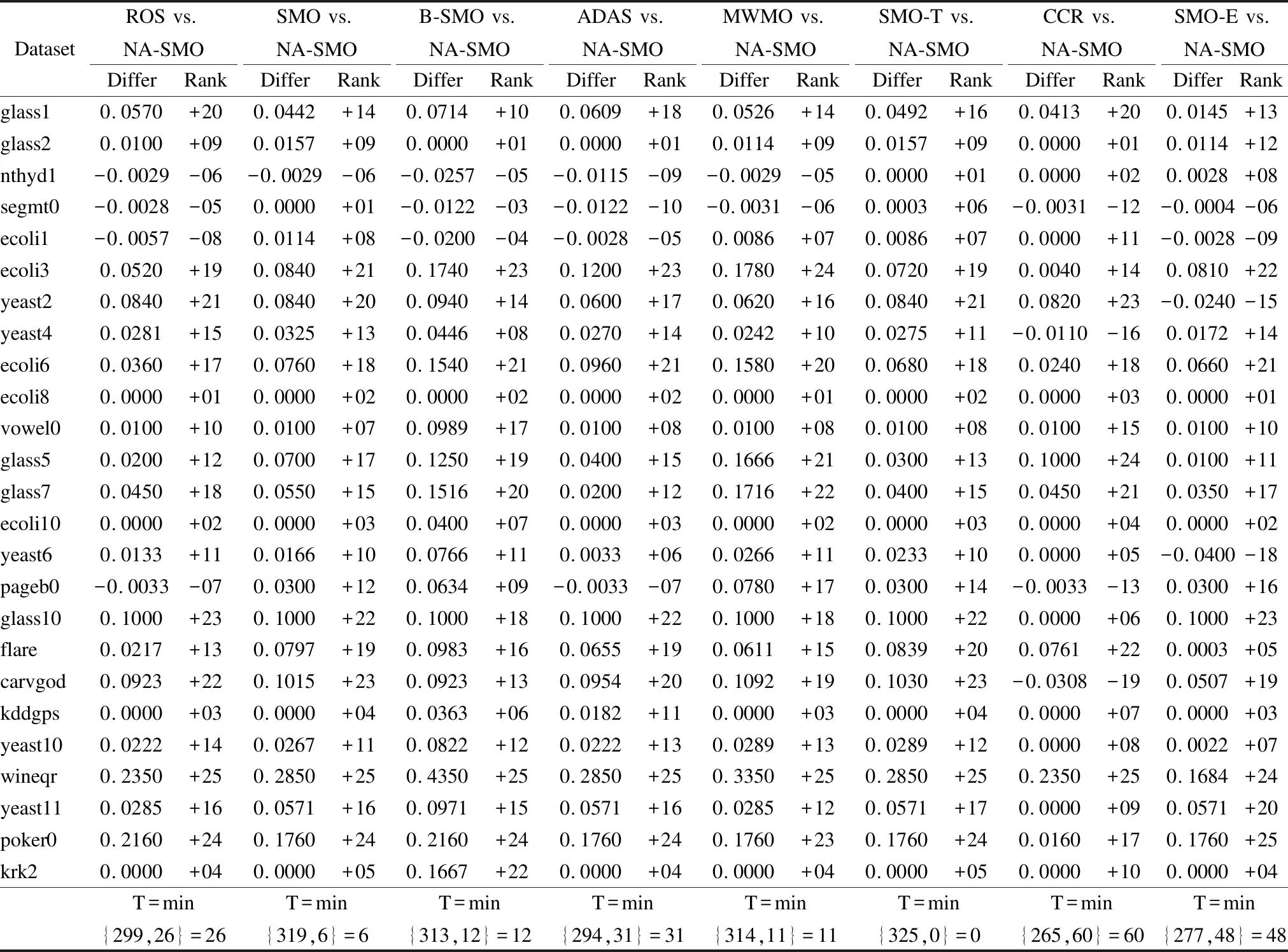
4.6 对比实验


5 总结与展望

