基于空间位置概率的NGSO通信星座干扰仿真分析研究

李伟 魏文康 刘畅 刘珊杉 武秀广

（国家无线电监测中心，北京 100037）

引 言

与5G无线通信网络相比，6G无线通信网络将有望提供100%的覆盖率，实现空天地海一体化网络[1]. 为满足全球无缝覆盖的需求，6G无线通信网络不只限于陆地无线通信网络，将与卫星通信、海洋通信和无人机通信等形成以地面网络为基础、以空间网络为拓展的信息网络[2]. 凭借空间立体广域覆盖、高通量大带宽，尤其是微小卫星制造技术的发展和卫星发射成本的降低，非静止轨道(non-geostationary orbit, NGSO)通信星座网络被认为是未来6G无线网络体系架构中一种有潜力的解决方案[3].

近年来，O3b、OneWeb、SpaceX和Telesat等欧美公司纷纷计划部署NGSO通信星座系统来提供高速率宽带互联网服务[4]，NGSO通信星座系统迎来了新一波高速发展浪潮，如OneWeb预计发射720颗卫星[5]；Starlink预计共发射约42 000颗卫星. 从世界各国向国际电联(International Telecommunication Union, ITU)申报的频率轨道资源技术资料来看，这些新兴的NGSO通信星座系统拟规划使用的频率资源主要集中在Ku/Ka频段. 同时，Ku/Ka频段也是传统静止轨道(geostationary orbit, GSO)卫星通信系统的主用频段，目前该频段上已运行着大量的在轨系统. 未来NGSO通信星座系统与GSO卫星通信系统同频共存的场景下，由于NGSO通信星座系统的卫星规模庞大，全球连续覆盖且用户终端无处不在，对GSO卫星通信系统造成有害干扰的可能性极大[6-10].根据ITU《无线电规则》第22.2条，GSO卫星固定业务系统和卫星广播系统在Ku/Ka频段使用上具有优先地位，NGSO卫星通信系统不得对这些GSO系统造成不可接受的干扰，且不得寻求GSO系统的保护.因此，开展NGSO通信星座系统与GSO卫星系统之间的干扰分析研究显得尤为必要.

国内外已经开展了NGSO通信星座系统与GSO卫星系统间的干扰分析研究. 针对GSO卫星系统的地球站接收到来自多颗NGSO卫星的发射信号下行链路场景，文献[6]分析了规避角策略对等效功率 通 量 密 度(equivalent power flux density, EPFD)的影响. 文献[7]在保证GSO系统不受干扰前提下，通过计算载噪比及干噪比对NGSO下行链路的可用性进行了分析. 文献[8]研究了NGSO星座系统与GSO卫星系统间的上下行共线干扰情况，并提出了基于功率控制的干扰减缓策略. 文献[9]分析了NGSO星座系统对GSO卫星系统的上行链路干扰.文献[10]针对NGSO星座系统干扰GSO卫星系统的端到端场景，研究了NGSO卫星数量以及NGSO卫星与GSO卫星间的相对角度对误码率(bit error rate, BER)的影响. 文献[11]提出了一种基于概率的干扰分析方法.

上述文献基本都是在特定干扰场景下针对星座系统中单颗或少数几颗NGSO卫星进行的干扰计算仿真，没有结合实际星座系统的轨道运行规律，进而难以对干扰仿真结果进行长时的统计分析，得到的仿真结果不能较为客观地反映实际干扰情况. 并且国内外规划建设的星座系统都是成百上千颗卫星组成，甚至还有万颗以上规模，如何高效分析这种大规模NGSO通信星座系统与GSO卫星系统之间的干扰也是当前面临的难题. 关于卫星系统的干扰仿真分析，国际上较为通用的软件工具Visualyse (Professional)在计算大规模NGSO通信星座系统时存在复杂度过高、仿真时间过长的问题. 文献[11]获得统计性干扰计算结果不需要计算机长时间的仿真来遍历整个星座，与通用软件仿真相比具有仿真时间短的优势，但在干扰建模时没有考虑NGSO通信星座系统的多波束建模和频率复用方案，且在对NGSO星座中的参考卫星进行空间采样时使用不变的单一精度.

针对上述问题，本文对NGSO通信星座系统与GSO卫星通信系统之间的同频干扰情况进行深入研究，建立了面向多波束NGSO通信星座系统的集总同频干扰场景数学分析模型，根据ITU的相关建议和报告，提出基于空间位置概率的双精度干扰分析方法. 通过对比分析验证所提方法的可信度及高效性，为大规模NGSO通信星座系统的干扰评估提供有效的分析方法并降低仿真复杂度.

1 干扰场景及干扰建模

图1为GSO卫星系统与NGSO通信星座系统间的下行干扰场景示意图.

图1 下行干扰场景示意图Fig. 1 Schematic diagram of downlink interference scenario

1.1 干扰场景数学模型

GSO地球站接收到来自单个NGSO卫星某个波束的下行链路干扰Idown为

式中：Pt表示NGSO卫星的发射功率；假设地球站天线主瓣对准其服务卫星天线，gns(θ1) 、gge(θ2)分别表示偏 离 天 线 主 轴 θ1、 θ2方 向 上 的 天 线 增 益，其 中 下 标ns表示NGSO卫星，下标ge表示GSO地球站；FBA表示下行链路的带宽调整因子；d2表示下行链路干扰路径的星地间距离； λ2表示下行链路载波频率对应波长.

由于NGSO通信星座系统卫星规模大，地面终端无处不在，存在多颗NGSO卫星同时干扰某个GSO地球站的情况；NGSO卫星采用多波束天线且卫星波束之间存在频率复用[12]，每个NGSO卫星覆盖范围内同时存在多条链路对GSO地球站产生有害干扰. 因此，在对NGSO通信星座系统和GSO卫星系统的下行干扰场景进行分析时，需要同时考虑来自不同NGSO卫星和不同卫星波束的同频干扰.GSO地球站受到来自NGSO卫星的下行链路集总干扰为

式中：Idown,ls表示第s颗NGSO卫星的第l个波束对GSO地球站产生的下行干扰；S表示对GSO地球站产生干扰的NGSO卫星数量；Ls表示第s颗NGSO卫 星下对GSO地球站产生干扰的波束数量.

1.2 干扰评价指标

干扰评价指标是判定两系统能否频率共用的判定标准. 常用的干扰评价指标有六种：最大允许集总干扰功率Iagg、 集总干扰噪声功率比RIN、噪声相对增量RΔTT、 EPFD、载波与集总干扰功率比RCI、BER. 前四种评价指标是面向频率协调，后两种是面向系统工作性能. 在后续分析中，选取ITU最常用的RIN作为干扰评价指标，来衡量系统干扰严重程度. GSO地球站受到来自NGSO卫星的下行链路集总干扰噪声功率比RIN为

式中：k表示玻尔兹曼常数；B表示受扰系统的下行链路通信带宽；T表示受扰系统地球站天线等效噪声温度. 集总干扰噪声功率比RIN的dB形式为

2 空间位置概率双精度算法

空间位置概率双精度算法(dual step algorithm of spatial position probability, DSA-SPP)采用双精度网格分辨率对经纬度网格进行空间采样，对每一个空间采样点进行干扰分析，从而得到具有空间统计特性的干扰结果. DSA-SPP可通过预先设定的NGSO参考卫星所处的空间网格位置求解得到NGSO星座的拓扑[11]. 由于干扰功率水平是NGSO卫星位置的函数，已知NGSO参考卫星在经纬度网格的概率密度函数，则可求解得到干扰功率水平的概率密度函数和累积分布函数(cumulative distribution function, CDF)，从而评估NGSO通信星座系统对GSO卫星系统的干扰程度. 鉴于NGSO通信星座系统的卫星规模庞大，干扰链路数量较多，为了兼顾仿真的准确性及高效性，DSA-SPP采用双精度：在干扰变化显著的区域采用精细网格分辨率，在干扰变化缓慢的区域采用粗网格分辨率.

2 .1 空间位置概率的精度分析

2.1.1 NGSO参考卫星的概率密度函数

已知参考卫星的位置，可以确定星座中其他卫星的位置，得到对应的星座拓扑. 考虑圆轨道，参考卫星位置关于经度 Φ和 纬度 Θ的联合概率分布函数[11]为

式 中，δ为NGSO星座的轨道倾角.

2.1.2 精细步长区域定义

依据ITU-R S.1325-3建议书[12]，精细步长区域φFSR是基于GSO地球站处观察到的分隔角来定义的.如图2所示，φFSR与地球站的天线尺寸有关，当D/λ＞100时，

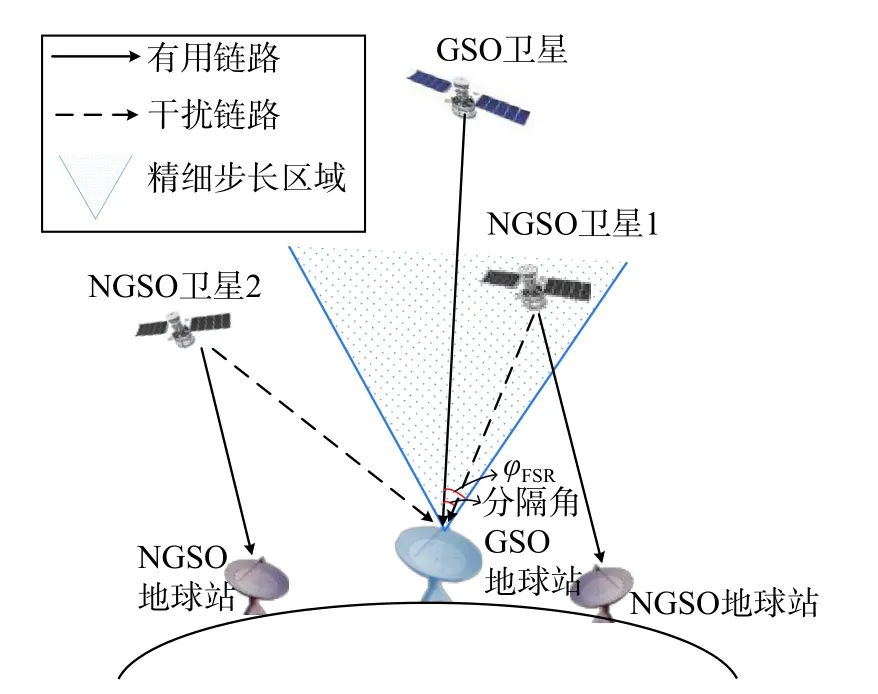
图2 精细步长区域示意图Fig. 2 Schematic diagram of fine step region

式中： α1为 第一旁瓣角度， α1=15.85(D/λ)－0.6，D为GSO地球站天线直径，λ为下行链路工作频率所对应的波长.

2.1.3 精细步长仿真触发准则

按照ITU-R S.1325-3建议书，对于GSO地球站em，只要有一颗NGSO卫星sn与GSO卫星之间的分隔角φm,n小 于等于φFSR，则应采用精细仿真步长. 当参考卫星位于经纬度网格gi,j时，DSA-SPP采用的精细步长仿真触发因子fi,j,m为

考虑到新兴NGSO通信星座系统的卫星数量巨大，对地具有多重覆盖，在GSO地球站em处，分隔角小于等于φFSR的NGSO卫星数量将会变多. 同时，为 了进一步提升仿真效率，在S.1325-3建议书定义的精细步长区域基础上，设计了基于分隔角小于等于φFSR的NGSO卫星颗数的精细步长仿真因子. 记q表示分隔角小于等于φFSR的NGSO卫星颗数占所有干扰NGSO卫星颗数的比例，当参考卫星位于经纬度网格gi,j时，DSA-SPP采用的精细步长仿真触发因子fi,j,m为

式中：qth表示准则所规定的门限值；S′表示分隔角小于等于φFSR的 NGSO卫星颗数；S表示对GSO地球站em带来干扰的NGSO卫星总颗数.

2.2 DSA-SPP流程

DSA-SPP流程如图3所示. 首先在(－π＜Φ≤π,－δ＜Θ＜δ)经度-纬度平面按照粗网格分辨率划分经纬度网格. 对于每次空间采样，假定参考卫星位于经纬度网格中心. 任意选取一个经纬度网格，将NGSO通信星座系统的参考卫星置于该网格中心，并根据式(5)计算出参考卫星出现在该经纬度网格上的概率. 已知参考卫星的位置，则可确定星座系统中其他卫星的位置，按照一定的跟星策略建立通信链路，NGSO通信星座系统与GSO卫星系统之间的干扰关系也就能够确定，进而可计算出该网格下NGSO通信星座系统对GSO卫星系统下行链路的集总干扰.遍历所有经纬度网格，得到在每一个网格下的集总干扰及对应概率，最终可得到RIN的CDF.

为兼顾干扰计算的精度与复杂度，在按照粗网络分辨率划分经纬度网络的基础上，在一定触发准则下，引入细网格分辨率. 在图3的步骤8，根据在GSO地球站观察到的GSO卫星与NGSO卫星之间的分隔角自适应调整经纬度网格分辨率，若分隔角小于等于式(6)的精细步长区域的夹角限值φFSR，则采用细仿真网格分辨率将参考NGSO卫星所处的经纬度网格作进一步划分，形成更细的经纬度网格，并按照前文描述的干扰分析流程分别计算每一个细经纬度网格下的集总干扰及相应的概率.

图3 DSA-SPP流程Fig. 3 Flowchart of DSA-SPP

3 仿真与结果分析

3.1 仿真模型

以SINOSAT-5系统和OneWeb系统为仿真场景. SINOSAT-5卫星的轨道位置为110.5°E，ITU卫星网络资料数据库中SINOSAT-5卫星网络资料ID为106520145[13]. 选取下行波束EKU1的参数信息作为SINOSAT-5系统下行链路的仿真参数配置，如表1所示.

表1 SINOSAT-5卫星系统通信参数Tab. 1 SINOSAT-5 satellite communication parameters

OneWeb系统的轨道高度为1 200 km，倾角为87.9°，有18个轨道面，每个轨道面有40颗卫星，共720颗卫星. 每颗OneWeb卫星具有16个固定波束[4-5]，波束采用时分复用传输方案，波束间采用八色频率复用. OneWeb卫星网络资料ID为113520120[16]，选取下行波束TAR3的参数信息作为OneWeb系统的 仿真参数配置，如表2所示.

表2 OneWeb卫星系统通信参数Tab. 2 OneWeb satellite communication parameters

3.2 精细步长仿真触发准则探究

DSA-SPP采用双精度分辨率来划分经纬度网格，需要确定精细步长仿真(即精细网格分辨率)触发准则. 根据式(7)至(9)，设置了三种不同精细步长仿真触发准则，以评估其对仿真结果的影响，如表3所示.

表3 双步长仿真触发准则Tab. 3 Simulation trigger criterions of dual step

基于OneWeb和SINOSAT-5系统参数，设置GSO地球站的位置为(0°，110.5°E)，采用均匀分布方式部署NGSO地球站28个(站间距160 km)，分析OneWeb系统对SINOSAT-5系统下行用户链路的干扰. 粗细仿真步长的经纬度分辨率分别为0.2°和0.01°. 图4 给出了不同精细步长仿真触发准则下GSO地球站集总干噪比RIN的CDF曲线. 可以看出，与单一粗步长相比，采用单一粗步长与细步长结合的双步长得到的RIN分布范围更广，尤其能够有效避免漏掉一些较为严重干扰情形的统计，如图4右上角的小图所示. 另外，在三种精细步长仿真触发准则下，GSO地球站集总干噪比CDF曲线完全重合. 这是因为当部署28个NGSO地球站时，分隔角小于等于φFSR的NGSO卫 星颗数占比q超过了20%.

图4 不同精细步长准则下 RIN 的CDF(28个NGSO地球站)Fig. 4 CDF of RIN with different fine step size criteria(28 NGSO earth stations)

图5给出了在NGSO地球站部署数目增为252个情形下GSO地球站集总干噪比RIN的CDF曲线. 由图5可知，准则1和准则2下的GSO地球站集总干噪比CDF曲线完全重合，准则3与它们并未完全重合，但相差甚微. 随着NGSO地球站部署数量的增多，干扰GSO地球站的NGSO卫星数量随之增加，致使在每次空间采样中分隔角小于等于φFSR的NGSO卫星数占比q均不小于10%，但不总大于20%.因此，在对大规模NGSO通信星座系统进行干扰分析时，可以通过设置稍微严格的精细步长仿真准则，在保证干扰计算结果精度的同时还可提升仿真效率.

图5 不同精细步长准则下 RIN 的CDF(252个NGSO地球站)Fig. 5 CDF of RIN with different fine step size criteria(252 NGSO earth stations)

3.3 仿真方法有效性及高效性探究

通过与国际通用工具Visualyse(Professional)的干扰计算结果作比较来验证所提方法的有效性.Visualyse(Professional)仿真步长分别设为10 s、1 s和0.1 s，总仿真时长3天，卫星数目为720颗. 仿真计算机配置如表4所示.

表4 仿真计算机配置Tab. 4 Computer configuration for simulation

DSA-SPP与Visualyse(Professional)仿真结果如图6所示. 可以看出，两种方法得到的结果趋势一致，仿真曲线基本重合，DSA-SPP与Visualyse(Professional)(0.1 s)得到的结果最为接近，说明利用DSA-SPP进行干扰分析是合理可信的. 从图6还可看出，采用DSA-SPP得到的RIN分布在-60～20 dB，比Visualyse(Professional)采用最精细步长0.1 s时统计得到的RIN分布范围更广，说明DSA-SPP的统计结果更为精确. DSA-SPP仿真用时27 min，Visualyse (Professional)(0.1 s)用 时1 801 min，说 明DSA-SPP仿真效率更高.

图6 DSA-SPP与Visualyse(professional)仿真结果对比Fig. 6 Comparison of simulation results between DSA-SPP and Visualyse (professional)

3.4 地球站位置对仿真结果影响探究

在[0°N，5°N，10°N，15°N，20°N]各部署1个GSO地球站，探究GSO地球站位置对干扰结果的影响，结果如图7所示. 可以看出，在0～20°N低纬地区，随着纬度增大，GSO地球站受来自NGSO通信星座系统的干扰程度不断减弱. 这是因为在0～20°N区域内，GSO地球站的集总干扰主要受OneWeb卫星的发送天线增益及SINOSAT-5地球站的接收增益影响. 干扰链路指向相对于OneWeb波束指向的离轴角变化小，干扰链路的发射增益变化不明显；GSO卫星波束指向其星下点位置，随着GSO地球站纬度增大，干扰链路相对于GSO卫星波束指向的离轴角也将增大，受扰链路的接收增益随之而减小.

图7 不同GSO地球站地理纬度干扰结果Fig. 7 Interference analysis of GSO earth station in different geographical latitudes

4 结 论

针对NGSO通信星座系统与GSO卫星系统下行用户链路之间的同频干扰，尤其是大规模星座系统同频干扰仿真效率不高的问题，建立了面向多波束NGSO通信星座系统的集总干扰分析数学模型.根据ITU的相关建议和报告，设计了DSA-SPP和精细步长仿真驱动准则. 以SINOSAT-5系统和OneWeb系统为仿真场景，与国际通用工具Visualyse (Professional)进行了结果校验. 仿真结果表明，相比通用国际工具，所提算法能够得到更大范围的干噪比，耗时更短，说明所提算法得到的统计结果更精确，仿真效率更高，更加适用于卫星颗数庞大的通信星座系统.

在DSA-SPP算法影响因素探究上，通过三种精细步长仿真驱动准则下的结果对比分析，证明对于大规模NGSO通信星座系统，采用准则3(即分隔角小于等于φFSR的NGSO卫星颗数占比门限为20%时)能够兼顾结果精度和计算效率. 在干扰分析结果影响因素探究上，GSO地球站的纬度位置分布对NGSO通信星座系统的下行干扰程度影响较大. 上述研究有望为大规模NGSO通信星座系统设计以及频率国际协调提供有益参考，下一步将重点研究如何减缓大规模NGSO通信星座系统对GSO卫星系统的干扰.