基于LSTM与多特征融合的高铁无线信道场景识别

王英捷 周涛 陶成

（北京交通大学电子信息工程学院，北京 100044）

随着我国交通的不断发展，高铁目前在我国占骨干地位，其中通信系统是满足铁路运营与乘客需求必不可少的部分. 近年来，用户对通信服务质量需求逐步提升，为了满足用户移动通信的需求，铁路下一代移动通信技术铁路长期演进(long-term evolution for railway, LTE-R)将在不久的将来成为铁路专用宽带移动通信系统主体[1]. 此外，5G的时代已经到来，5G系统将支持各种高速场景的应用，因此也非常适宜部署在高铁上，满足乘客在5G时代对通信服务的各类需求.

高铁列车沿线通过多个场景[2]，根据电磁波传播特性，高铁信道场景具体被划分成12类：高架桥、U形槽、车站、隧道、丘陵、乡村、郊区、城市等[3]. 此外，有作者提出一种在高铁通信系统中出现的特殊场景：多链路场景[4]. 各种不同的传播场景对应了电磁波在其中不同的传播特性，影响着通信系统的性能[5]. 如果无线通信系统能够智能地识别出当前的传播场景，则通过一些自适应技术，如自适应调制与编码，并结合资源分配与调度，可以有效地提高系统整体性能. 因此，信道场景识别对于高铁无线通信网络的设计十分重要.

机器学习作为一种在自然语言、图像领域被大量使用且效果显著的算法模型，目前在无线通信信道领域应用仍然不多. He Ruisi等人采用一系列聚类算法对信道功率延时谱中的多径分量进行聚类分析，提出了多种针对高速场景下的聚类算法，并取得了良好的聚簇性能[6]. Bai Lu等人在Q频带下实施了信道测量，并使用人工神经网络(artificial neural network, ANN)对不同天气、场景的信道参数进行了预测. 统计结果表明，98.8%的预测数值与其对应的测量结果误差小于1 dB[7]. 上述内容聚焦于信道多径分量的聚簇研究、簇模型和多径簇生灭追踪，以及针对某一特定场景的信道特征参数预测估计. 而本文中我们聚焦于目前成果较少的信道场景识别研究.目前已发表的主要成果如下：M. I. AlHajri等人将信道转移函数(channel transfer function, CTF)与频率相关 函 数(frequency correlation function, FCF)作 为 特征，使用K近邻(K-nearest neighbor, KNN)与加权K近邻(weighted K-nearest neighbor, WKNN)针对室内的不同场景进行了识别[8]，最终发现WKNN在测试集数据中的表现最佳，达到了99.8%的识别准确率. 文献[8]的识别内容仅仅考虑了几种简单的机器学习方法而未涉及深度学习的模型，且文中并未明确其提出的方法能够同样用于时变信道的识别，也并没有考虑特征融合的方式. 除此之外，针对高速场景下不同传播环境的识别仍然较少，因此本文将针对这一独特场景下的不同传播环境，通过多特征融合的方式进行识别.

本文基于4G-LTE专网测量下信道实测数据，使用深度神经网络与多特征融合的方法对不同信道场景进行分类与识别. 首先给出了测量数据的来源及信道小尺度特征的提取方法，发现每种特征都对应着一种信道特性，即莱斯因子(K-factor, KF)对应了信道衰落程度，均方根时延扩展(root-mean-square delay spread, RMS DS)、均方根多普勒扩展(root-meansquare Doppler spread, RMS DPS)与均方根角度扩展(root-mean-square angular spread, RMS AS)分别刻画了信道的时-频-空域的色散程度，他们共同描绘了不同场景的信道特性. 通过上述的特征提取过程，我们认为不同特征对识别的性能有着不同的影响，因此我们考虑多特征融合的方法，其中包括了前融合、前馈式融合、后融合，最后在后融合基础上提出赋予不同特征不同权重的加权平均后融合方法，并结合特征序列式数据特点，将全连接层替换为了长短时记忆(long short term memory, LSTM)层. 相较于传统机器学习方法和几种常用的特征融合方法，该模型在识别准确率、曲线下面积(area under curve, AUC)两大指标上均达到最优性能，有在高速场景实际应用的潜力，可为未来高铁无线通信专网提升系统整体性能.

1 高铁无线信道典型场景

本文中所使用的信道测量数据为基于京-津线沿线LTE网络信道探测所获得的测量数据[9]. 京-津线总长120 km，其中约86%的铁路位于高架桥之上，平均车速约350 km/h. 列车所经过的场景包括乡村场景、车站场景、郊区场景，同时有一部分时间处于多链路场景之下. 因此本文仅考虑以上四种典型的场景.

1.1 场景介绍

1) 乡村场景

平原场景是京-津高铁线上最常见的场景，由于地面崎岖不平，铁轨被建造在距离地面10～15 m的高架桥上，且高架桥的高度远高于其周围的树丛与稀疏建筑物. 考虑到LTE基站高度约为30～50 m，此时收发端无线信号的主要传播为视距(line-ofsight, LoS)传播，少量的非视距传播(non-line-ofsight, NLoS)分量来自于列车行驶远离基站后高架桥附近出现的稀疏散射体建筑物与一些具有一定高度的密集树丛.

2) 车站场景

由于在京-津线上车站的数目十分稀少，测量时往返多次得到了3个车站的多次测量数据. 测量数据所对应的三个车站为典型的半开放式带顶棚的车站类型.

3) 郊区场景

郊区场景是介于平原与城市之间的一种场景.与平原场景相比，郊区场景具有更加丰富的反射物与散射物，如高层的建筑物、铁轨两侧高密的树丛等. 而与城市场景相对比，郊区场景建筑物的密集程度类似，但是高度相对较低.

4) 多链路场景

多链路场景是京-津高铁线上的一种特殊场景，它与列车所处的实际外在环境无关. 为了减少列车行驶过程中移动终端的频繁小区切换，高铁组网时，人们将几个以相同频率发送相同信号的物理小区合并为一个逻辑小区，列车行驶在逻辑小区中物理小区的重叠区域时，移动终端会收到来自于相邻两个甚至多个小区基站同时发送的信号，这些重叠区域的场景则作为一种多链路场景，也被收集到我们的数据库中.

1.2 信道特征参数的提取

本文信道特征参数均是从信道测量获取的原始信道冲激响应(channel impulse response, CIR)数据中得到的.

1) KF

KF是信道衰落程度的度量，它是信道冲激响应中直射分量与非直射分量的功率之比. 我们通过传统的矩估计算法来获取窄带KF[10].

2) RMS DS

RMS DS是表征无线信道时间色散的重要参数.它为功率延时谱的二阶中心距的二次根，即标准差.

3) RMS DPS

RMS DPS经常被用于衡量无线信道频率色散的程度，与RMS DS一样，它为多普勒功率密度谱的标准差.

4) RMS AS

无线信道的空间色散程度通常通过RMS AS来进行衡量，它通过计算功率角度谱的标准差获得.

四大特征刚好从四大角度来对无线信道进行刻画，包含了衰落程度与空-时-频特性，因此我们使用四大信道特征作为机器学习的输入特征，对无线信道场景进行识别.

1.3 数据集概述

经过上述特征提取，我们获得了四种场景所对应的信道特征数据集. 数据集中的每个数据都对应了一个LTE基站的覆盖，并进行了场景的标记. 四种场景的数据集如表1所示.

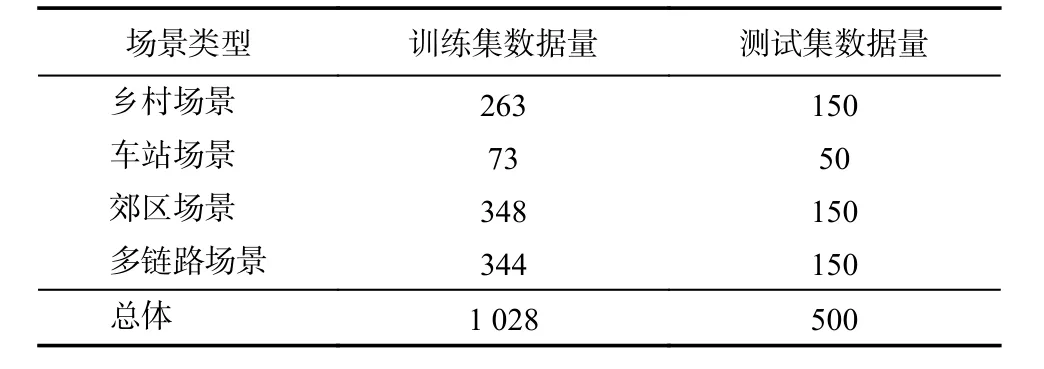
表1 四种场景的数据集Tab. 1 Training and testing datasets

我们一共获取了1 528组数据，它们被分成1 028组训练数据与500组测试数据. 其中，这些数据所对应的基站并不是独立的，测量过程中我们在京-津线经过了多次往返，每一个基站所对应的信道场景都经过了多次采集.

2 多特征融合神经网络算法

仅仅考虑一个特征(KF、RMS DS、RMS DPS、RMS AS)来进行信道场景识别是无法得到较为理想的效果的. 因此我们使用多特征融合的方式，在充分利用信道空-时-频特性的条件下进行识别. 我们参考了在多媒体中基于多特征的人体动作识别与针对RGB的多特征影像识别中的三种常用的特征融合算法[11]，它们分别是前融合、前馈式融合、后融合，三种融合方式的详细架构图如图1所示.

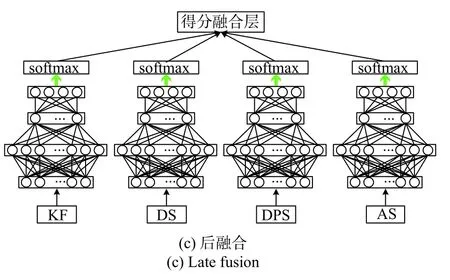
图1 三种融合方式架构示意图Fig. 1 Architecture of three fusion schemes

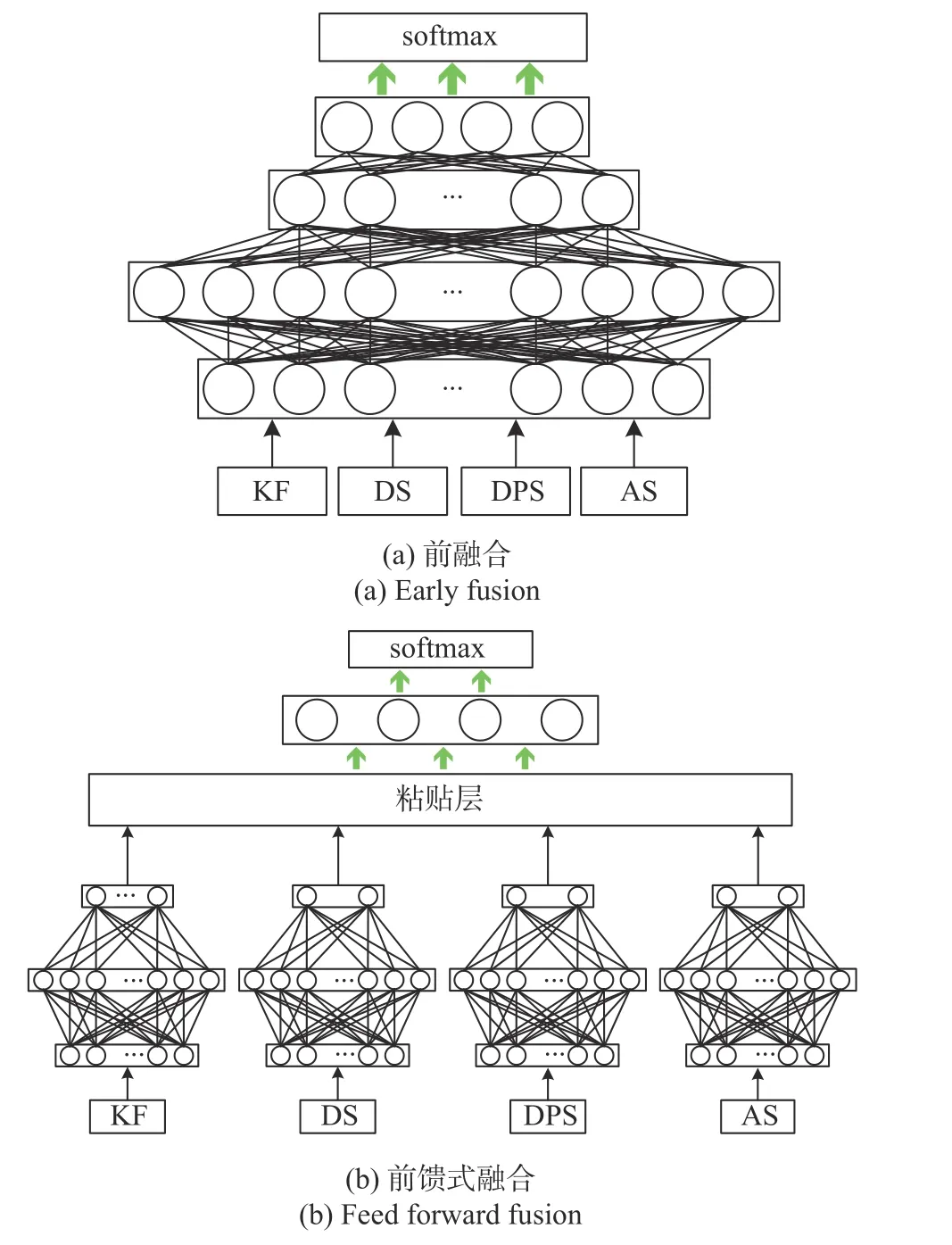
由图1可知：前融合是将所有特征无差别地拼合，再进行识别；前馈式融合将特征在输入时独立化地进行处理，在输出端融合其转换后的表征，相较于前融合，前馈式融合考虑了特征的独立性，但是引入了额外的权重参数，也加大了计算的复杂度；后融合是将输出的四个置信度得分向量进行平均，它最大的优势在于相对较少的参数量. 然而，不同特征对识别性能的贡献程度很可能是不同的，后融合这种基于置信度得分向量平均化的融合方式仍然无法取得最优的性能，因此我们考虑使用加权平均后融合的方法，并将全连接层替换成广泛应用于序列式数据的LSTM网络.

2.1 LSTM加权平均后融合

如上文所述，考虑到获取的信道特征流具有序列特性，而LSTM网络是一种广泛应用于序列数据的神经网络变体，且能够克服普通循环神经网络中出现的梯度弥散问题[12]，因此我们将后融合与LSTM网络相结合，提出了基于LSTM的加权式平均后融合网络模型，并用于高铁场景下的信道场景识别.

LSTM网络中，每一个单元都与普通的神经网络神经元不同，其中包含了大量运算.

图2为一个带有窥视孔机制[13]的LSTM基本细胞单元的内部架构，有：

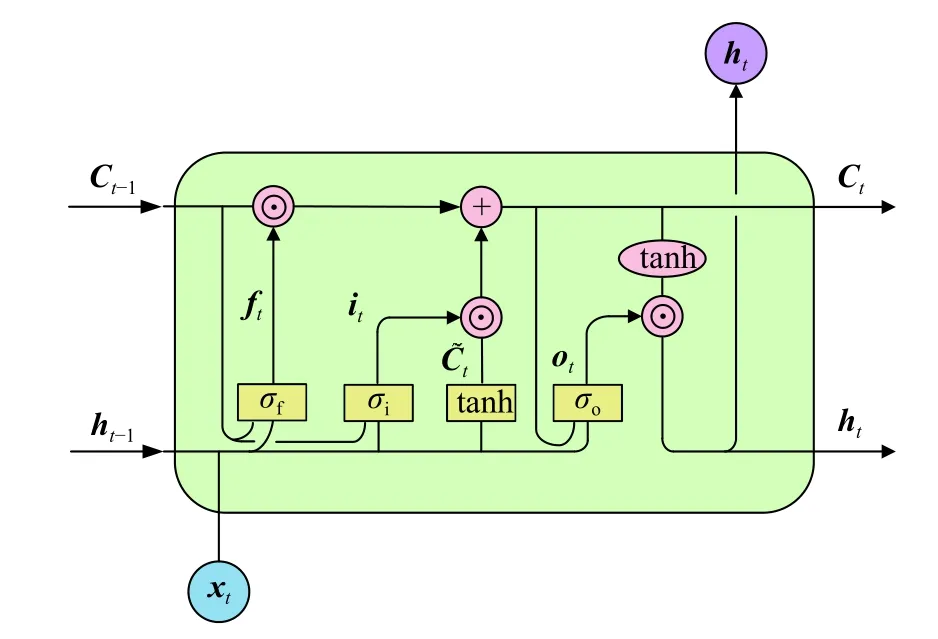
图2 带窥视孔的LSTM细胞单元基本架构Fig. 2 Basic structure of a single LSTM cell with peephole connection

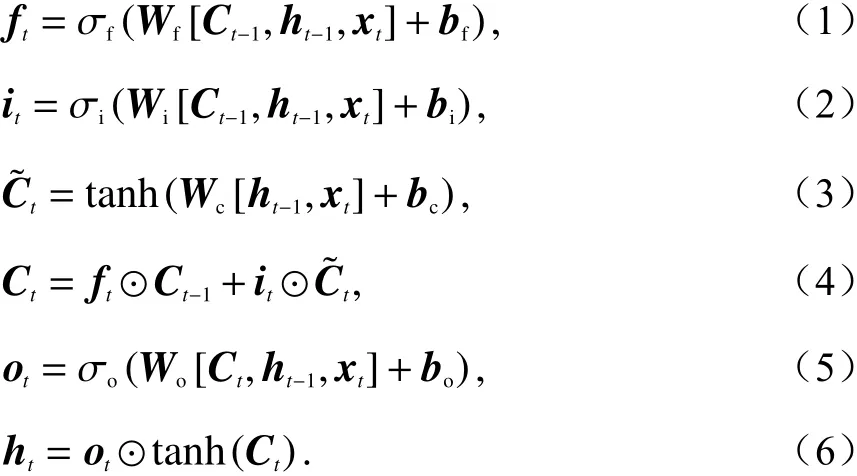
式中： σ(·) 代 表一个门控单元函数， σf(·)为遗忘门，σi(·) 为输入门， σo(·) 为 输出门；f t为遗忘门的输出；i t为 输入门的输出；Ct为当前t时刻的细胞状态，它会被送入下一个时刻的LSTM细胞单元；o t为输出门的输出；h t为 当前t时刻的隐藏状态，也是当前t时刻的输出，同时它被送入下一个时刻的LSTM细胞单元；⊙表示对应元素相乘； [ ·]表示矩阵之间的粘贴运算.

如图3所示，每一层的LSTM网络中包含多个LSTM细胞单元，它们代表高铁行驶到某一时刻的状态，我们将每个时刻所采集到的信道特征数据输入LSTM细胞单元中并进行传递.

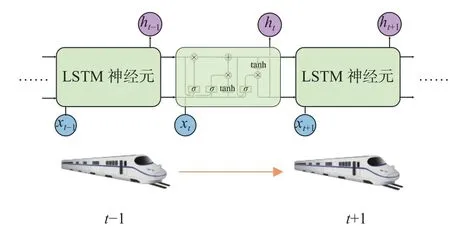
图3 信道特征在每一层LSTM细胞单元中的传递Fig. 3 LSTM architecture for channel feature streams

图4为将加权平均后融合与LSTM网络结合后的结构，我们将第n个 样本的第k个特征流输入并经过三层LSTM与softmax层后输出的置信度得分向量表示为

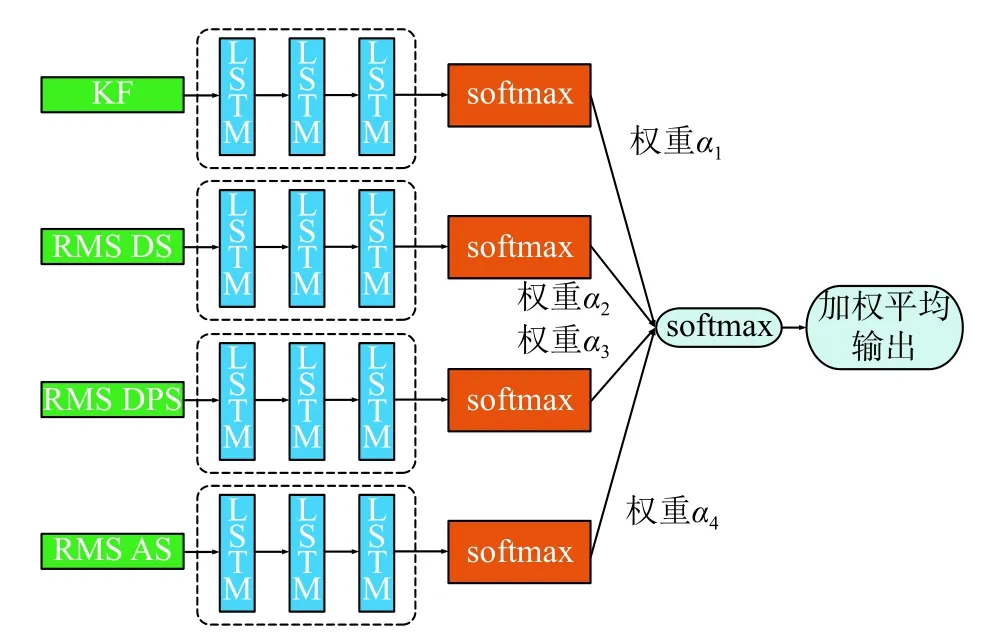
图4 加权平均后融合模型架构图Fig. 4 Architecture of weighted score fusion based LSTM model

式中：C是数据中场景类型的总数，本文中为四种典型场景，即C=4；K是输入特征流的数量，本文中使用1.2节中描述的四大尺度特征，即K=4. 设yˆ是将四种信道特征独立输入后，最后在输出端经过加权后的最终置信度得分向量，有

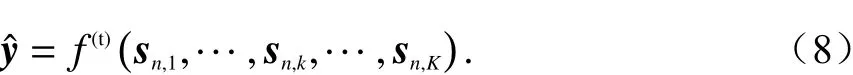
式中：f(t)(·)为一个转换函数，它可以是线性的(如本文中的线性加权函数)，也可以是一个非线性的(如径向基函数、sigmoid函数等).

为了达到模型中加权平均后融合的效果，我们首先按前面所述的后融合的方式对多层LSTM进行训练，获得K个与不同信道特征相对应的置信度得分向量，并将其整合为一个矩阵. 假设第n个训练数据输入后所得的置信度得分矩阵为

接下来我们定义在每一个特征流输入后的输出端被赋予的权重为 αk，那么权重向量α=[α1,···,αK]∈RK将会在输出端所额外增加的一个softmax层中得到学习并优化以获得不同特征流输出向量的最优组合方式. 因此网络的损失函数将通过两个步骤来最小化其交叉熵. 其中交叉熵函数H(·)的具体定义如下：

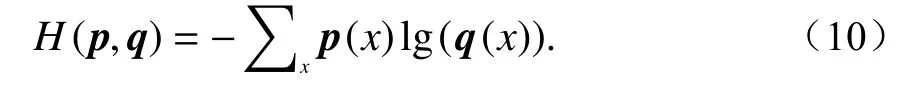
式中：p为 理想结果即正确标签向量；q为识别模型输出结果，即经过softmax转换后的置信度向量，它们都是一种概率分布.

训练的第一步是通过类似后融合的方式获得每一个特征流输入后的置信度得分向量，此时损失函数的最优化目标为

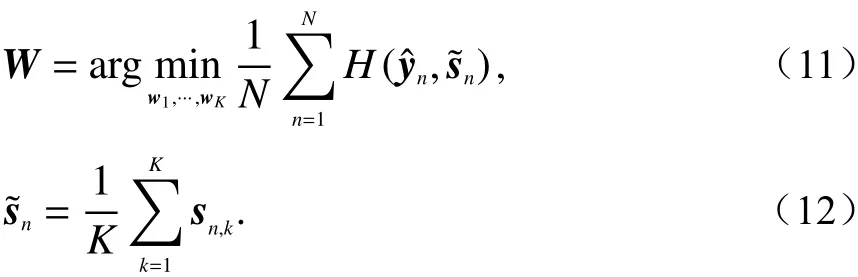
式中：N代表训练集中数据的总数；yˆn表示第n个训练数据的实际标签向量；s~n表示第n个训练数据的平均置信分数向量.

第二步则是在得到每个特征相应的置信得分向量基础上，优化之前所提到的权重向量 α，在获得加权后的向量之后，让其再次通过一个softmax层，这是因为我们要将得分进行一次归一化以获得合理的置信度得分结果. 最终得到的第n个训练数据在softmax输入端的加权置信得分向量vn为

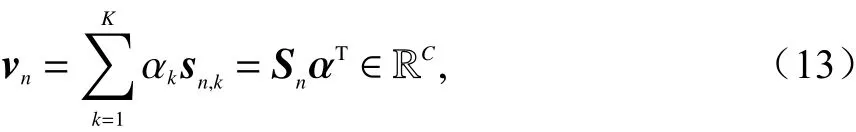
此时损失函数的最优化目标为

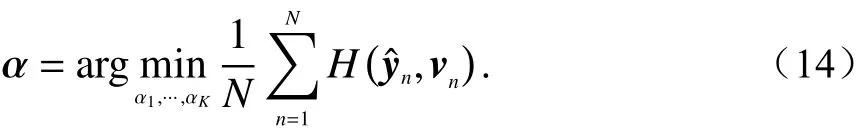
需要注意的是，在第一阶段所得到的权重W与偏置项在第二阶段的训练中都处于被冻结的状态，它们的值将不会在训练时改变，这种二阶段冻结权重的训练模式是一种非常直接的减轻过拟合现象的方式. 假设融合前的网络架构都为三层的LSTM，单层LSTM复杂度为O(W)， 其中W=4n2c+4ni×nc+nc×no+3nc，nc为 LSTM单元中神经元个数，ni为输入维度，no为输出维度[14]. 四种融合方式的时间复杂度如表2所示.

表2 四种融合方式的时间复杂度Tab. 2 Computational complexity of 4 fusion schemes

表2中Ne为额外全连接层的神经元数量，Nf为特征流的数量，通常认为Ne≫Nf，本文中Nf为4. 相较于前馈式融合与后融合模式，这种加权平均后融合的方式在一定程度上可以被认为是二者权衡下的模型 ，复杂度介于二者之间.

2.2 模型具体参数设置

式中：Nl表示第l层 神经元个数；U[·]表示均匀分布.而 网络中所有的偏置项全部被初始化为0.

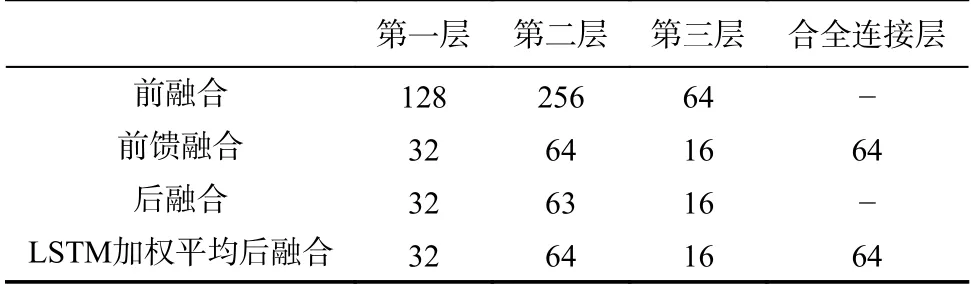
表3 不同融合方式的模型每层神经元个数Tab. 3 The number of neurons at each layer in different fusion schemes

初始化之后，网络中的所有权重与偏置项在训练过程中都要通过梯度相关的算法进行更新，本文使用适应性矩估计(adaptive moment estimation，Adam)算法来进行更新[15]. 与传统的梯度下降算法(如随机梯度下降)不同，Adam算法通过计算梯度的一阶矩估计和二阶矩估计为不同参数设计的自适应性学习率，它适用于包含高噪声或者稀疏梯度的问题，超参数也具有较强的可解释性，并且只需要极少量的参数调整即可立即应用.

训练完毕后，人们通常设置验证集以观察模型性能并决定是否选择其他模型，或是调整一些超参数. 本文采用的是分层k折交叉验证的验证算法. 我们设k为5，这种情况下，训练集中20%的数据将被划分为验证集，验证集中包含的每一种类别场景所占比例与它在总体测试集中所占比例相同，因此测试集与划分出来的验证集将具有相同的样本状态.通过分层五折交叉验证算法的验证，我们发现当网络中每一种特征流后面的隐藏层数量超过三层时，性能与三层相仿，并没有明显提高，而模型中每多一层隐藏层，就会引入额外的计算复杂度；反之当层数降低，则性能出现比较明显的下滑. 具体的识别准确率结果如图5所示.

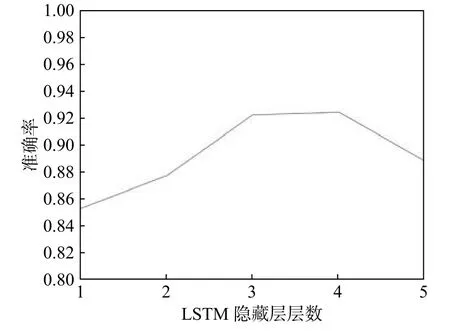
图5 不同LSTM层数下模型的识别准确率Fig. 5 Accuracy under different number of LSTM layers

因此我们采用每个特征流后接三个隐藏层的方式 ，以权衡模型性能与复杂度之间的矛盾.

机器学习中最常用的评价模型性能指标就是整体预测识别准确率. 但是针对样本不平衡的状况时，我们需要几种评估指标共同进行评价.

3.1 混淆矩阵

混淆矩阵又被称为误差矩阵，它是一种特殊的以表格形式来可视化不同算法、模型性能的矩阵. 矩阵中每一列表示模型最终预测的类别，每一行表示测试集数据实际的标签.

我们使用的基于LSTM加权式后融合的混淆矩阵如图6所示，可以看到：8%的郊区场景被误预测为多链路场景；8%的多链路场景被误预测为了郊区场景，其他场景之间的识别误差情况相对较低. 由于数据中存在样本不平衡的情况，因此仅仅通过识别准确率与混淆矩阵来衡量模型性能是不全面的，以下我们将使用更多指标来综合地评判.

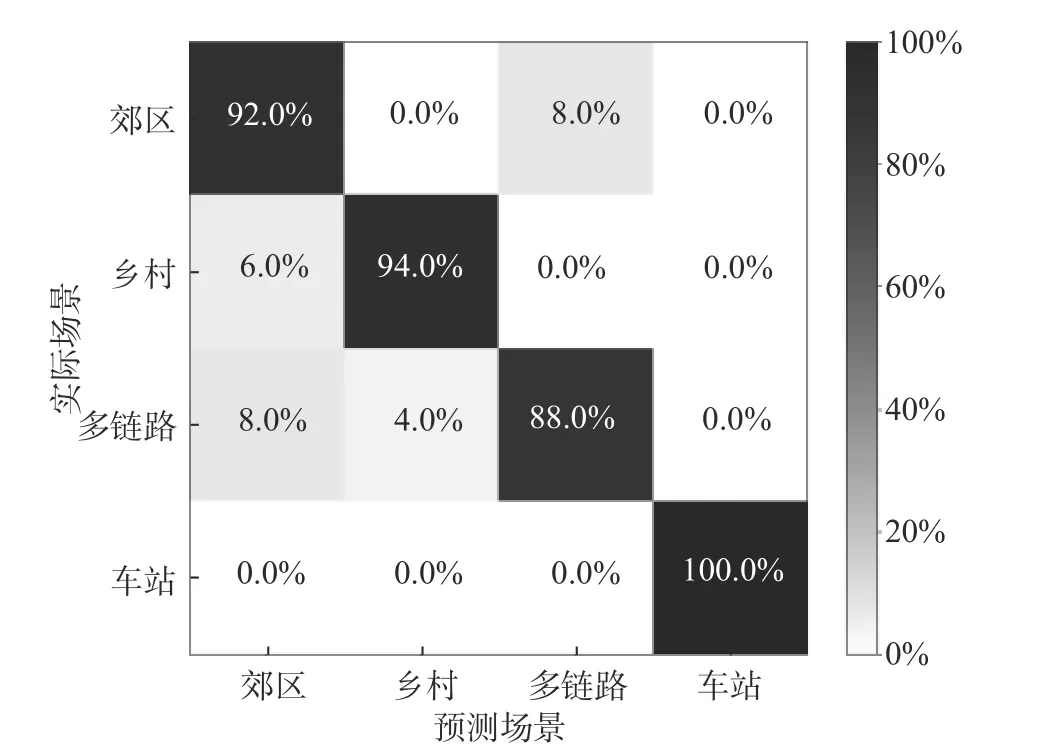
图6 基于LSTM的加权平均后融合算法混淆矩阵Fig. 6 Confusion matrix of weighted score fusion based LSTM model

3.2 ROC曲线

受试者工作特征(receiver operating characteristic,ROC)曲线是一种更加高阶的分类模型性能评估方式，它通常通过曲线图来直观展示. ROC曲线最直观的画法就是将所有样本按模型打分从高到低排序，然后将每一个样本的置信度得分定为上述进行硬判决的阈值，其从1到0连续变化，是模型的真正率与假正率的同步变化曲线，通常坐标轴的横轴为假正率，纵轴为真正率. ROC曲线与横坐标以及纵坐标正半轴所围成的封闭区间面积被称为AUC，通过计算，AUC的实际物理意义为分类器Ci将一个测试集中随机抽取的正例排序于测试集中随机抽取的反例之前的概率[16]：

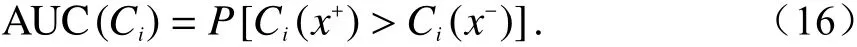
AUC越高，正例相比反例得到更高的置信度的可能性就越大；AUC越接近于1说明预测性能越好；AUC为0.5时说明分类器是将所有测试数据进行了随机预测，是性能最差的状况. AUC在一定程度上也可以被认为是模型鲁棒程度的度量，AUC越高，模型鲁棒性越好. 而且，AUC可以用于衡量模型在样本不平衡下的性能.

从图7可以看到，基于LSTM的加权平均后融合的ROC曲线与坐标轴围成的面积最大.

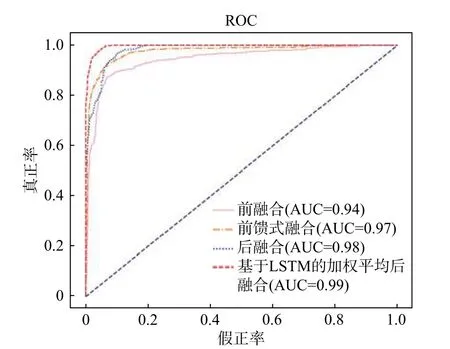
图7 各种融合方式的ROC曲线Fig. 7 ROC curves of different multi-feature fusion schemes

最后，各种模型的所有指标结果在表4给出，可以看出，基于LSTM的加权平均后融合的神经网络考虑了不同特征对识别性能的贡献度差异，所有指标均获得了最优的性能，其中识别准确率达到了92.2%. 同时，使用多特征融合的神经网络性能优于传统的机器学习算法，如随机森林、WKNN和SVM.

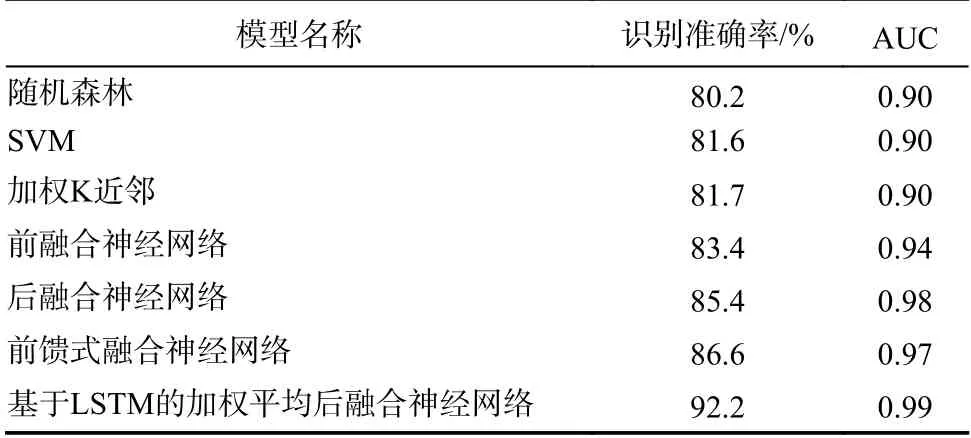
表4 不同融合方式与常用机器学习模型的性能Tab. 4 Performance of multi-feature fusion schemes and regular machine learning models

4 结 论

本文研究了基于机器学习的高铁无线信道场景识别方法. 文中提出的基于LSTM的加权平均后融合模型在文中所构建的高铁无线信道数据库的测试集上达到了92.2%的识别准确率，AUC值为0.99，优于几种常见的融合方法与常用机器学习算法. 通过上述数据集构建的内容，我们发现无线信道典型场景数据库中车站类型的单一化仍是一个尚待解决的问题. 同时，通过混淆矩阵可以看到，多链路与郊区场景之间有相对明显的误预测，所以在以后的研究中我们将对不同信道场景之间的相关性进行分析.