5G毫米波频段不同天线形式信道参数测量及对比分析

刘永胜 侯春枝 林乐科 张蕊， 张鹦琪

（1. 中国电波传播研究所，青岛 266107；2. 西安电子科技大学，西安710071；3. 齐鲁理工学院，济南 250220）

引 言

2019年以来5G已经成为迄今为止商用部署速度最快的一代无线通信技术，据市场调研机构IDC公司预测，2023年全球5G连接数将超过10亿，比4G获得同样连接数的时间整整快了两年. 由于低频段在网络覆盖和建设成本上的优势，当前中国、欧洲和韩国等国家均将Sub-6 GHz作为5G商用网络的主要建设频段，美国的部分运营商将毫米波频段作为试点网络建设. 要实现高于10 Gbit/s的峰值数据速率、1 000 Mbit/s的用户体验速率和毫秒级时延等关键技术指标，毫米波和Massive MIMO是未来5G网络部署中必须要采用的关键技术[1-2]. 为了验证新技术的效能以及提高系统设计效率，需要建立符合毫米波频段传播特性的信道模型.

毫米波频段电磁波传播损耗大，容易受到障碍物、反射物、散射体以及大气吸收等环境因素的影响，因此毫米波信道与传统移动通信频段信道有着明显不同，其传播特性影响到系统性能和覆盖方案的设计，需要精确的测量和分析. 国外针对毫米波频段的信道特性测量与分析建模工作开展较早，美国纽约大学、芬兰阿尔托大学、德国伊尔梅瑙工业大学、东京工业大学等科研机构开展了不同频段、不同场景的信道测量工作. 纽约大学的Rappaport教授团队的测量频段和场景覆盖较为全面[3-6]，测量频段包括28 GHz、38 GHz、60 GHz、72 GHz和73 GHz，测量场景包括室内、郊区、城区等环境. 国内华北电力大学赵雄文教授团队开展了一系列室内外毫米波测量及信道建模工作[7-9]；北京邮电大学利用矢量网络分析仪和喇叭天线开展了室内毫米波频段信道特性测量[10]；同济大学利用信道探测仪开展了室内72 GHz的信道测量工作[11]；南京邮电大学利用射线追踪技术开展了毫米波频段传播特性研究[12]；北京交通大学开展了高速移动场景下的毫米波信道特性研究[13]；中国电波传播研究所开展了毫米波频段地物损耗研究以及雨衰减研究[14-15].

由于毫米波自身的传播特性限制，为了增大测量距离，以前的信道测量中往往采用喇叭天线来提高增益. 喇叭天线按照一定角度间隔(通常为半功率波束宽度)顺时针或者逆时针旋转一周，之后采用非参数化或参数化方法进行信道参数提取. 喇叭天线旋转测试被称为定向扫描探测(directional scan sounding,DSS)，该方法的缺点是测量耗时. 在进行Massive MIMO测量时，由于毫米波频段时域信道测量设备成本限制，通道数一般不会过多，因此通常采用虚拟MIMO的方法进行测量，该方法在假定测量时信道环境不发生改变. 不同天线形式对信号接收效果不同，因此同一环境下的信道测量结果也会产生差异，例如采用喇叭天线旋转测量方式，可以接收水平面360°内的全部有效信号；但采用阵列天线时，贴片天线只能接收水平面180°范围内的信号. 接收端在利用全向天线进行信道测量时，由于天线增益较喇叭天线低数十分贝，在发射功率不变的前提下，会丢失部分多径信号. 现有文献中，同一环境同一位置的测量只采用一种天线，没有多种天线形式下的信道测量结果对比和定量研究，因此，不同研究者提供的室内外的信道参数会有所不同.

基于统计建模方法的毫米波信道模型，其准确度依赖于统计参数的精度. 在信道参数测量过程中，不同天线具有不同的特性，采用的测量方法也不尽相同，因此相同环境下提取的信道参数有所差别. 本文基于室内28 GHz、38 GHz频段全向天线、喇叭天线以及阵列天线的信道测量数据，利用高分辨率参数提取算法空间交替广义期望最大化(space-alternating generalized expectation-maximization, SAGE)算法对信道参数进行提取，利用多径分量距离(multipath component distance, MCD)方法进行簇提取，对比分析了路径损耗(path loss, PL)、时延扩展(delay spread, DS)、角度扩展(angel spread, AS)以及分簇结果的不同，该结果可为室内毫米波频段不同天线形式信道测量结果提供对比分析数据.

1 测量系统及测量过程

5G毫米波频段可用带宽高达数GHz，如此高的带宽给信道测量设备带来很大挑战. 传统的宽带信道测量方法主要包括直接脉冲测量、扩频滑动相关测量以及频域扫频测量，其中扩频滑动相关测量方法在提高处理增益和覆盖范围方面有很大优势，成为毫米波信道测量的主流方法.

本次采用的测量系统为扩频滑动相关测量系统，其具备毫米波频段多天线宽带信道测量能力，通过GPS驯服铷钟进行同步，收发端可分离划定测量点，进行远距离测量，系统配备三维天线转台，可对天线垂直、水平以及俯仰三个维度进行精确控制. 本次测量过程系统参数如表1所示. 测量地点选择中国电波传播研究所办公区，实测环境如图1所示. 发射端放置于办公区一侧，接收点在过道区域选定测量点，由于室内有边长80 cm的承重柱，因此在测量路线上可划分视距(line-of-sight, LoS)测量点和非视距(nonline-of-sight, NLoS)测量点.

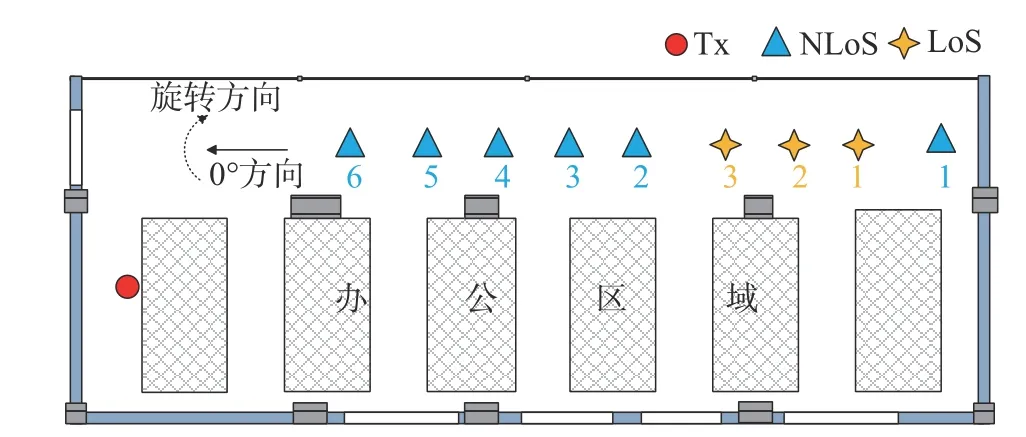
图1 测量场景示意图Fig. 1 Schematic diagram of measurement scenario

表1 测试参数Tab. 1 Measurement parameters

接收端利用喇叭天线进行DSS测量时，喇叭天线顺时针方向水平旋转，角度间隔为5°，参考方向为0°，见图1. 进行阵列天线测量时，天线阵列法线方向指向发射天线，本次测量中阵列天线在水平方向和垂直方向均移动8次，每次移动距离为半波长，组成8×8=64单元虚拟阵列天线. 喇叭天线DSS和虚拟阵列天线测量示意图如图2和图3所示.

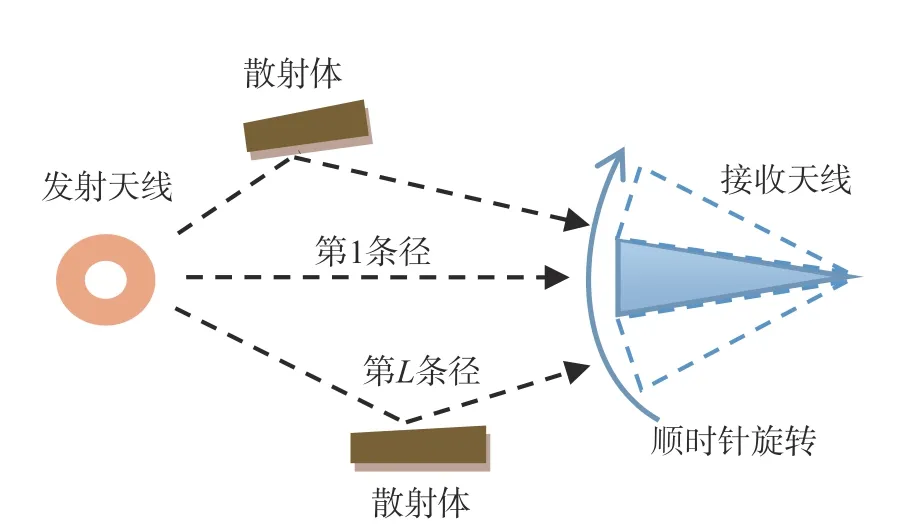
图2 喇叭天线DSS测量示意图Fig. 2 Schematic diagram of horn antenna DSS measurement

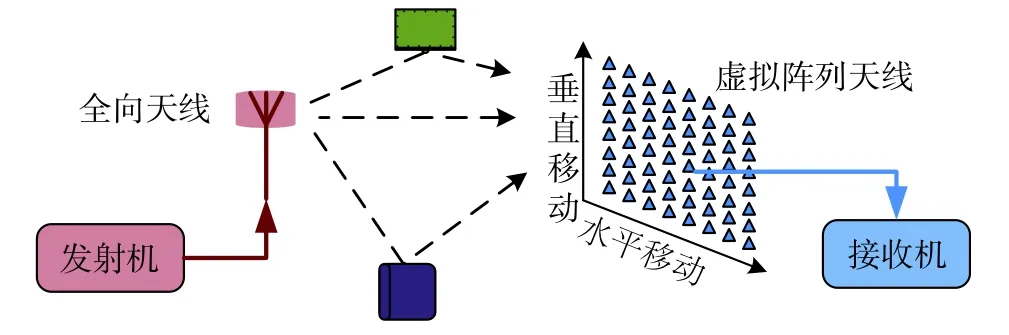
图3 虚拟阵列天线测量示意图Fig. 3 Schematic diagram of virtual array antenna measurement

2 信号处理过程

测量系统采用扩频滑动相关测量法，在发送端发送有良好自相关性的伪随机(pseudo-random sequence, PN)序列，接收机接收后采用与发送端相同的PN序列对接收信号进行相关运算，在去除系统响应后，可得到测试环境的信道冲激响应(channel impulse response, CIR)h(t,τ)，然后通过非参数化方法和参数化方法进行信道参数提取. 非参数化方法先将测量得到的信道冲激响应转化为功率延迟剖面(power delay profile, PDP)，再通过理论公式计算各信道参数. 参数化方法采用SAGE算法提取多径参数，算法通过最大化目标函数，可以估计出每条径上入射 波的各种参数.

2.1 信号模型及SAGE算法

在虚拟阵列天线测量过程中，可将天线单元位置假设为r1,r2,···,r N，则信号目标函数为

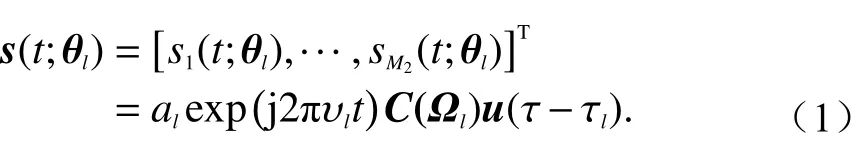
式 中： θl=[Ωl,τl,vl,al]是 第l条 散 射 波 的 参 数 矢 量；al、υl、Ωl、τl分别表示复振幅、多普勒频率、到达方向、传 播 时延；u(τ－τl) 是 发送 信 号矩 阵；C(Ω)是Ω方向入射角的响应矩阵，

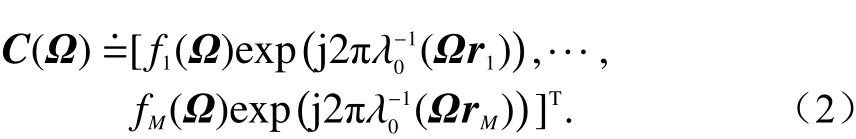
式中，fm(Ω)代 表接收天线第m个阵元的复电场模式.

单位方向矢量 Ω由球坐标中水平角 φ和垂直角θ确定：

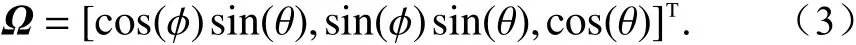
接收端天线阵输出信号可以表示为

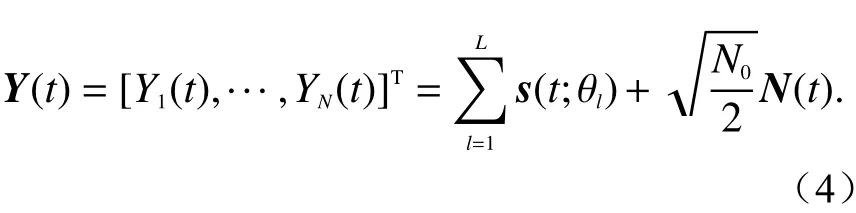
式 中：N(t)=[N1(t),···,NN(t)]T表示N维 高 斯 白 噪 声；N0为正的常数.

在DSS测量过程中，假设测量环境不发生变化，则多普勒频移为0，信号目标函数可以表示为

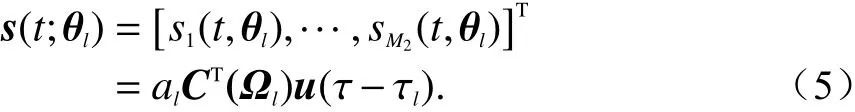
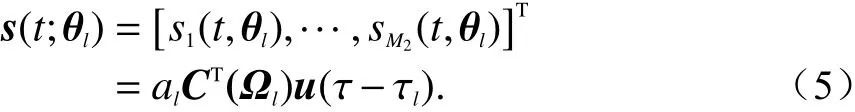
由于喇叭天线旋转时馈源位置不变，可以假定在坐标系原点，即r m=[0,0,0]，因此入射角的响应矩阵可以表示为

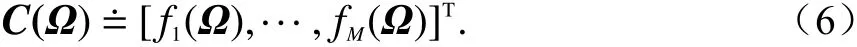
SAGE算法是期望最大化(expectation maximization, EM)算法的一个快速求解算法. EM算法基本思想是：首先根据己经给出的观测数据，估计出模型参数的值；然后依据上一步估计出的参数值估计缺失数据的值，再根据估计出的缺失数据加上之前己经观测到的数据对参数值重新进行估计；然后反复迭代，直至最后收敛，迭代结束. SAGE算法的具体实现过程包括初始化、E步骤和M步骤. SAGE算法的初始化可以得到各个参数的初始值，常用的初始化方法有连续干扰消除法和全零初始化两种.连续干扰消除法是一种比较精确的初始化方法，首先设置第l条路径的参数为

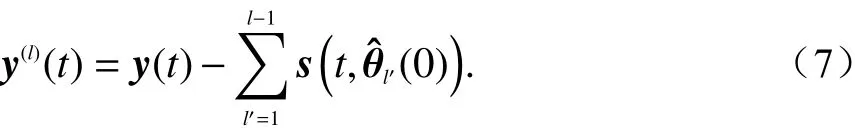
SAGE算法的E步骤，即求期望步骤，是基于观察到的不完备数据集Y(t)=y(t)估计不可观察到的完备数据Xl(t)=xl(t). SAGE算法的M步骤，为进一步降低运算复杂度，将联合优化过程分割成更小空间维数，在具体实现过程中定义为一维. SAGE算法各步骤具体过程见文献[16-17].

在DSS测量过程中，假设测量环境在测量过程中保持不变，多径分布完全由传播环境决定而与接收天线和旋转步长无关，因此各朝向测得的信道冲激响应相叠加，等效于使用合成的天线方向图测得CIR，在数据后处理过程中，去除天线增益的影响后 ，可准确地得到CIR[18].

2.2 分簇算法

在毫米波宽带信道测量及参数分析中，由于带宽达到数百兆甚至更高，多径分辨率为纳秒级，毫米波宽带信道测量可以观测到更多的多径信号. 目前国际上主流的信道建模方法为基于几何的统计模型(geometry-based statistical model, GBSM)，在GBSM信道建模方法中，每个簇包含一定数量的多径，簇的数目、簇内多径数量、簇内DS以及簇内AS等参数对信道模型准确度都有重要影响，因此准确地进行簇的分析和参数提取有重要意义. 当前主要的分簇算法有人工观察法、K次方均值(K power means, KPM)法和MCD方法. 文献[19]中给出了改进后的MCD分簇算法，在LoS场景通过设定双阈值的方法，提高了分簇准确度，具有较高的实用价值. MCD分簇算法简要介绍如下：

式中：ζ为时延域距离与角度域距离的比例因子；Ω为到达角方向矢量，由式(3)确定；τ为多径时延；στ为 τ的 标准差；Δ τmax为最大附加时延，

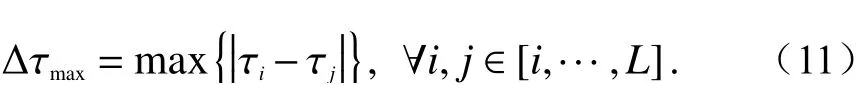
完整的分簇过程包括以下三个步骤：

1)在所有可分辨多径中选取功率最强径作为参考径；

2)计算所有剩余多径分量与参考径的分量距离，若小于给定的阈值，则划分为一个簇；

3)将已归为一簇的多径分量从多径集合中去除，重复步骤1和步骤2，直到所有多径分量全部被划 分完成.

2.3 信道参数

基于GBSM方法的信道模型中，需要重点考虑DS、AS、莱斯K因子以及簇的统计特性.

均方根(root-mean-square, RMS)DS στ定义为PDP二阶矩平方根[20]，其计算方法如下：

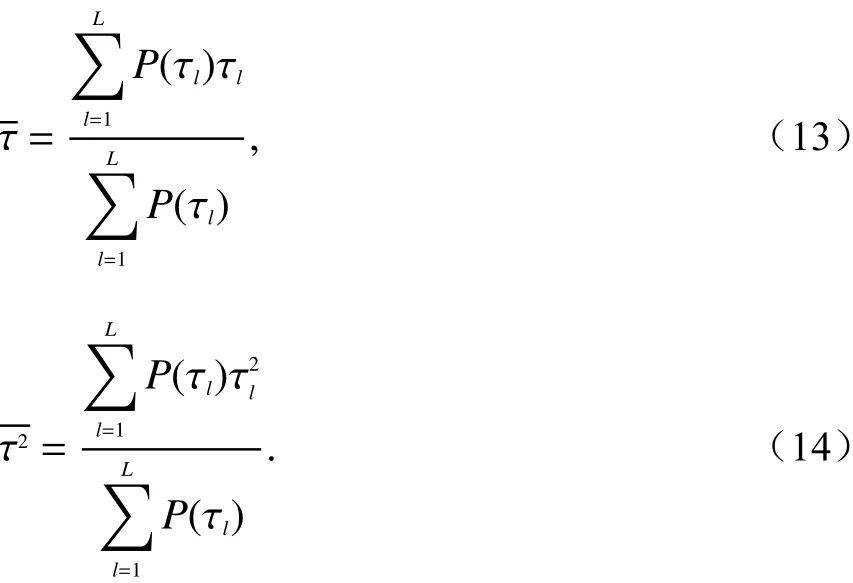
式中：τ为平均附加时延；L表示多径总数；P(τl)是归一化功率延时谱上第l条多径的功率值. 噪声对DS计算影响很大，如果噪底太高，会把部分有效信号当作噪声去掉；如果噪底太小，会将噪声计算在内.

与RMS DS类似，RMS AS σφ定义为角度功率谱的二阶中心矩的平方根[21]. 为避免角度循环周期特性造成的影响，将AS定义为循环AS，有

3 测量结果分析

3.1 PL对比

在5G系统的关键技术中，波束成型技术是提高信号覆盖和信道容量的重要手段，因此方向性PL在系统设计中具有较高的参考价值. 本文在分析喇叭天线测量结果时，采用的是喇叭天线最强信号方向的信号功率值，而非各朝向合成后的全向信号功率值. 通过后期数据处理，可以得到喇叭天线最强信号方向. 表2给出了28 GHz、38 GHz相同位置点喇叭天线、全向天线以及阵列天线的PL结果.可以看出：LoS场景下，全向天线PL最小，喇叭天线PL最大；NLoS场景下，全向天线依然最小，但喇叭天线和阵列天线相差不大. 其根本原因是全向天线可以接收到水平360°范围内的全部有效信号；而喇叭天线的半功率波束宽度只有7.5°，即便喇叭天线可以旋转找到信号最强的方向，但是不能接收全部多径信号，去除天线增益后依然不能达到全向天线的接收信号强度. 同样，阵列天线只能接收180°范围内的有效信号. 因此，喇叭天线和定向阵列天线测量得到的PL相对全向天线偏大.

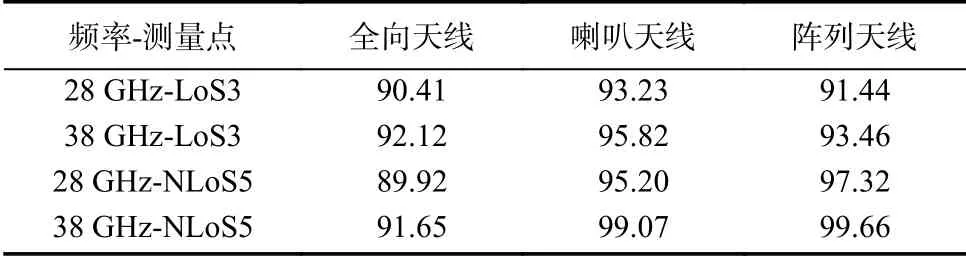
表2 不同形式接收天线的PL对比Tab. 2 Path loss results of different receiving antenna forms d B

3.2 DS对比

根据前面介绍的SAGE算法原理和信号模型，利用测量得到的CIR结果，可以提取多径信号的时延、水平到达角、垂直到达角以及幅度. 由于喇叭天线DSS时只在水平面测量，因此没有垂直到达角的信息. 图4给出了喇叭天线在LoS场景第3测量点28 GHz频段DSS的CIR测量结果.

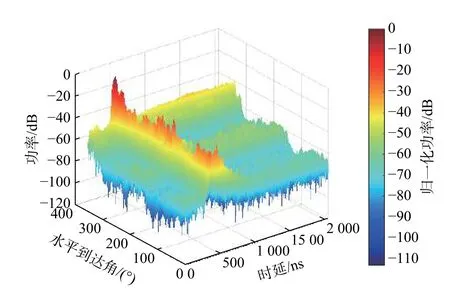
图4 喇叭天线LoS场景第3测量点DSS CIR结果Fig. 4 DSS CIR result of horn antenna at the 3rd measurement point in LoS scenario

表3给出了28 GHz、38 GHz相同位置点全向天线、喇叭天线和阵列天线的RMS DS结果. 可以看出，LoS场景下，全向天线测量得到的DS最大，阵列天线测量得到的DS最小，这是由于全向天线相对阵列天线来说，能够接收360°范围内的全部多径信号，且多径分量丰富，但同时由于全向天线增益相对喇叭天线小很多，有效信号动态范围较喇叭天线小，喇叭天线接收时信号主径效应明显，因此喇叭天线测量得到的DS比全向天线小. NLoS场景下，DS主要受多径信号丰富性影响，喇叭天线较其他天线具有最大的增益，能够接收最多的多径信号，因此DS值最大，而阵列天线最小.

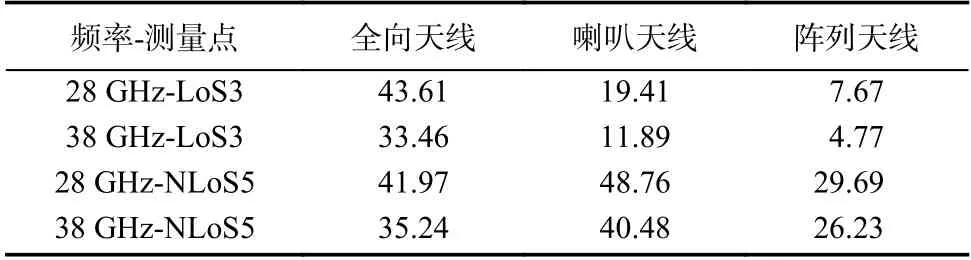
表3 不同接收天线形式下RMS DSTab. 3 RMSDS results of different receiving antenna forms ns

3.3 AS对比

表4给出了28 GHz、38 GHz相同位置点喇叭天线和阵列天线的RMS AS结果. 本次测量中喇叭天线只有水平方向的旋转，没有俯仰角信息，因此对比的角度信息只有水平到达角. 由表4可以看出：不管是喇叭天线还是阵列天线，NLoS场景下的同频段AS都要比LoS场景AS大，这是因为NLoS场景下接收信号都是反射信号或者散射信号，角度分布范围比较大；而LoS场景下有一条功率最大的直达径，弱化了其他NLoS路径的影响. LoS场景下，喇叭天线AS大于阵列天线AS，一方面是因为喇叭天线在旋转过程中，可以接收360°全方位的信号；另一方面，喇叭天线增益相对较高，可以接收到更多弱信号.

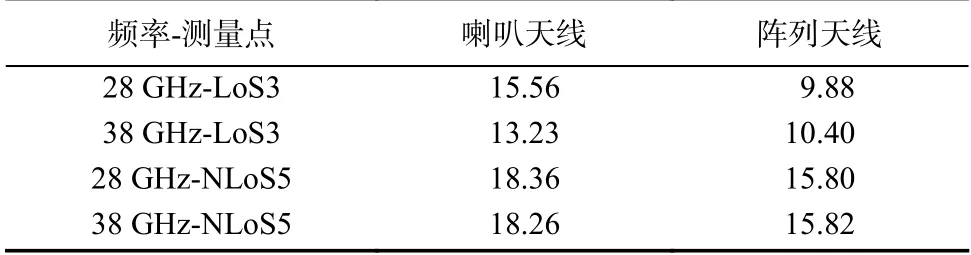
表4 不同接收天线形式下RMS ASTab. 4 RMS AS results of different receiving antenna forms d B

通过对多个测量点的RMS DS和RMS AS进行统计平均，可以得到不同频段不同天线形式下的定量比较. 由于喇叭天线测量结果相对于全向天线具有更大的实际意义，因此表5只给出了喇叭天线与阵列天线的比较结果，差值均为喇叭天线测量值减去阵列天线测量值.

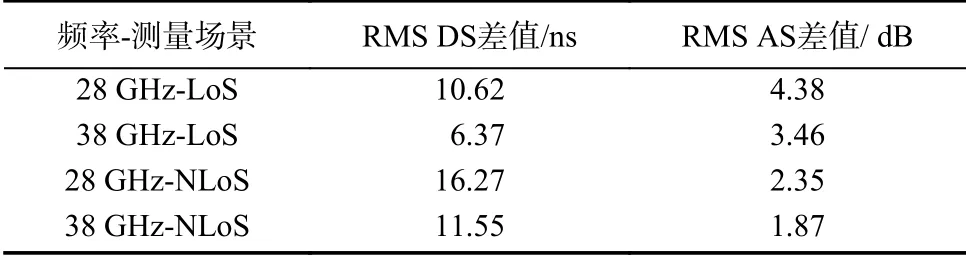
表5 喇叭天线与阵列天线小尺度参数对比Tab. 5 Comparison of small-scale parameters of horn antenna and array antenna

3.4 分簇结果对比

基于SAGE算法提取的信道参数，利用MCD方法进行簇提取. 经过多次比较，计算时比例因子 ζ =5，阈值dmin=0.25，选取的原则是分簇结果与实际环境相符，阈值取值与文献[19]相同. 图5是28 GHz频段LoS场景下第3测量点喇叭天线DSS测量和阵列天线测量得到的分簇结果. DSS测量下可得到时延超过100 ns的簇，这些簇来自于墙面或物体反射；而阵列天线受限 于接收方向和天线增益，未能得到超过40 ns的簇.

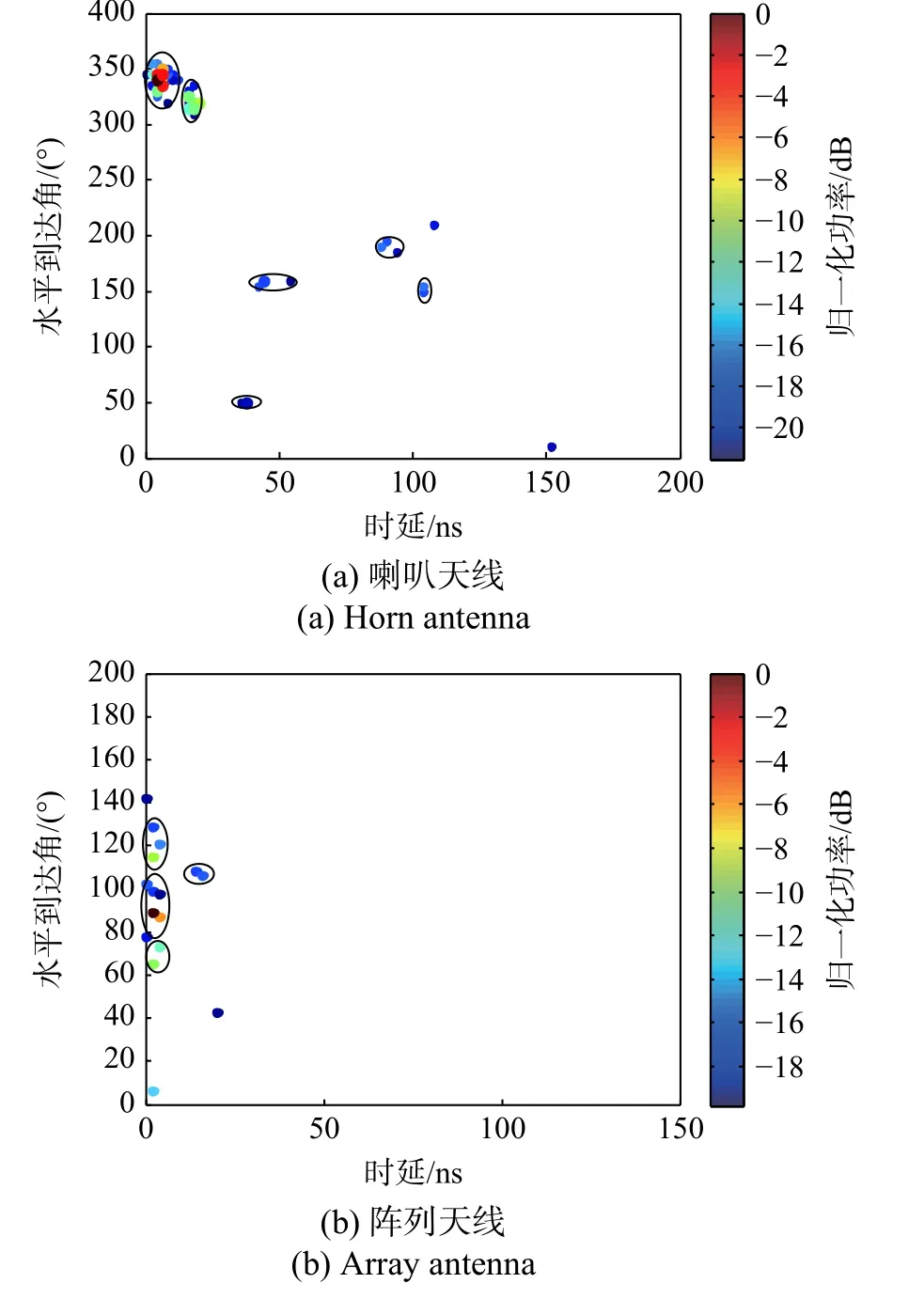
图5 LoS场景第3测量点喇叭天线DSS测量和阵列天线测量的分簇结果Fig. 5 Horn antenna DSS measurement and array antenna clustering results at the 3rd measurement point in LoS scenario

喇叭天线和阵列天线采集信号的角度范围不同，喇叭天线增益大且可以接收360°范围内的全部多径信号，而阵列天线只能接收到天线法线方向180°范围内的多径信号，因此采用喇叭天线旋转测量方式可以采集到时延域和角度域更大的多径信号.同时由于绝对零度的方向不一致，两种形式接收天线分簇结果差别明显.

如图6所示，28 GHz频段NLoS场景下第5测量点存在与LoS场景相同的现象，即喇叭天线DSS测量可以得到时延较大的簇. 同时，由于NLoS场景下多径信号全部来自于物体反射或者散射，多径到达信号比较分散，因此各个簇的水平达到角与LoS场景相比较为分散.

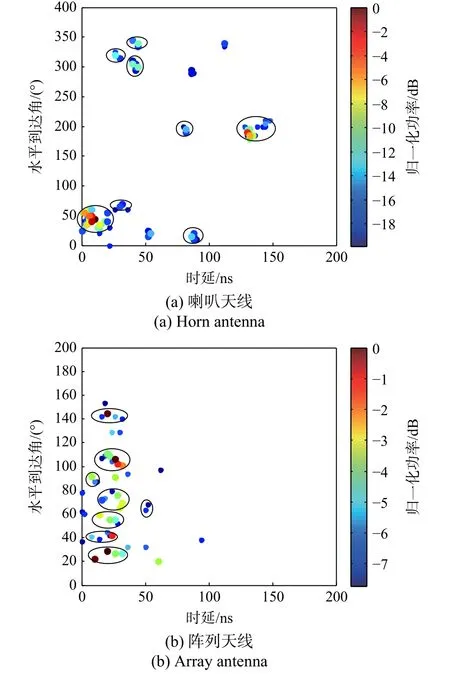
图6 NLoS场景第5测量点喇叭天线DSS测量和阵列天线测量的分簇结果Fig. 6 Horn antenna DSS measurement and array antenna clustering results at the 5th measurement point in NLoS scenario

4 结 论

本文基于28 GHz、38 GHz室内宽带信道测量数据，对室内毫米波频段不同天线形式信道测量结果进行了对比分析，基于SAGE算法和MCD分簇方法对簇进行了提取. 结果表明：不同天线形式对大尺度信道参数和小尺度参数具有不同影响，喇叭天线由于可以接收360°信号且增益较大，在DS和AS方面与全向天线和阵列天线明显不同；同时，喇叭天线的指向性较强，通过其测量得到的PL指数在5G系统波束成形技术应用中具有重要意义. 在分簇结果方面，阵列天线由于只能接收天线法线方向180°信号，导致无法提取天线背面多径信号，因此未能提取到时延较大的簇. 本文为室内毫米波频段信道建模提供了不同天线形式的信道测量参数，可为相关研究人员提供数据支撑.