毫米波时变信道仿真中实现空间一致性的方法研究

元媛 何睿斯 艾渤 钟章队

（1.北京交通大学电子信息工程学院，北京 100044；2.北京交通大学 轨道交通控制与安全国家重点实验室，北京 100044）

引 言

如今，随着世界范围内5G的快速发展以及无线通信载频的不断提高，需要更多的频谱资源用于通信技术的发展. 由国际电信联盟(International Telecommunication Union, ITU)举办的2019年世界无线电通信大会(World Radiocommunication Conference, WRC-19)就5G拟采用的毫米波频段设置达成了共识，将24.25～27.50 GHz、37.0～43.5 GHz、66～71 GHz毫米波频段主要用于5G移动通信发展[1]. 对于5G毫米波信道而言，传统的信道模型及仿真方法已经不能满足其仿真及通信系统性能评估的需求，需要根据毫米波的传播特性开展毫米波信道的仿真研究.

5G毫米波信道的仿真对于5G无线通信的发展至关重要. 在毫米波频段，当终端移动时多普勒频移较之低频段将会变得更为严重，从而导致信道相干时间减少，信道中多径分量(multipath components,MPCs)的路径损耗、时延、角度和功率等参数随移动距离变化很快，大尺度参数与小尺度参数都需要进行不断地更新[2]. 因此，在毫米波时变信道的仿真中准确实现空间一致性仿真的方法研究尤为重要.空间一致性描述的是当发射端或接收端移动时，信道的大尺度与小尺度参数随距离进行连续更新的特性[3]. 在现有的大多数模型中，通过引入相关距离来建立大尺度参数之间的相关性，但是对于小尺度参数，依旧根据信道测量数据所统计出的分布类型随机生成，这种方法带来的问题是即使离的很近的两个接收机，产生的信道小尺度参数之间也会缺乏相关性[4]. 因此，如何建立大尺度参数之间的相关性与小尺度参数的平滑演进是毫米波信道仿真中实现空间一致性的一大难题. 由于毫米波信号频率高、波长短，在传播过程中损耗较大，因此，毫米波在传播过程中多径的生灭更加剧烈且往往具有稀疏性[5-6]，毫米波信道中的空间一致性的仿真更加困难. 对于毫米波技术而言，空间一致性的仿真实现还有助于多用户或移动用户波束赋形及波束跟踪技术的设计，能够辅助提高波束跟踪的准确率[7-8]. 因此，毫米波信道仿真中关于空间一致性的方法研究具有重要意义.

目前，有许多组织和研究机构已经致力于空间一致性的研究[9]. COST2100信道模型是基于几何的信道模型，在该模型中，所有用户共享一组散射体，通过刻画散射簇的位置来仿真MPCs的特性. 该模型将散射簇分为本地簇和远端簇，当终端发生移动时，本地簇发生变化，远端簇不变，通过几何的方法计算MPCs[10]，从而可以实现信道空间一致性的仿真，但是由于该模型实现空间一致性方法的计算过程复杂且缺乏实测场景数据，因此，不适合运用到毫米波时变信道中空间一致性的仿真方法中. WINNER II信道模型通过信道测量结果计算出信道参数的统计概率分布从而仿真信道[11]，其基于大量的信道实测得到，但是该模型不支持空间一致性. 德国Fraunhofer HHI实验室提出的QuaDRiGa信道模型在WINNER II的基础上，增加了空间一致性的仿真[12-13]，且支持毫米波信道的仿真. 该模型首先生成具有相关性的大尺度参数，然后根据Drifting模型计算最后一跳散射体的三维位置，从而实现时延、角度和相位的连续更新，进而实现信道空间一致性的仿真. 但是关于Drifting模型的计算复杂度较高. 纽约大学的研究团队提出NYUSIM信道仿真器[14-16]，其适用于毫米波频段信道的仿真，且支持空间一致性的仿真. 该仿真器将信道的时变特性建模为MPCs的动态变化，首先将终端移动轨迹进行分割，其次生成连续仿真窗口间具有空间相关性的大尺度参数，最后基于移动距离进行小尺度参数的更新，使得信道参数平稳演进，从而实现了空间一致性的仿真. 但是该信道仿真器中连续仿真窗口间信道参数的相关性比较欠缺.

本文开展了毫米波时变信道仿真中关于实现空间一致性的研究. 首先，将终端移动轨迹进行分割，进行连续仿真窗口间大尺度参数相关性仿真，同时，引入M步3-状态马尔可夫链实现了窗口间多径簇数目的动态演化；然后，基于多径的几何分布结构实现小尺度参数的平滑演进，进而实现毫米波信道中空间一致性的仿真；最后，通过多径簇数目的自相关系数以及时延角度功率谱来衡量信道仿真时空间一致性仿真重现的准确性. 结果表明该仿真方法可以准确刻画5G毫米波信道的空间一致性. 本文的相关工作为5G毫米波时变信道仿真中空间一致性的实现提供了重要的依据.

1 毫米波信道仿真

在本节中，基于现有的通用5G毫米波信道模型[14]，随机生成毫米波信道中MPCs的功率、时延和空间角度等参数，从而实现毫米波信道的仿真. 图1为毫米波信道仿真的流程图，基本的仿真实现过程将在下面进行详细介绍.

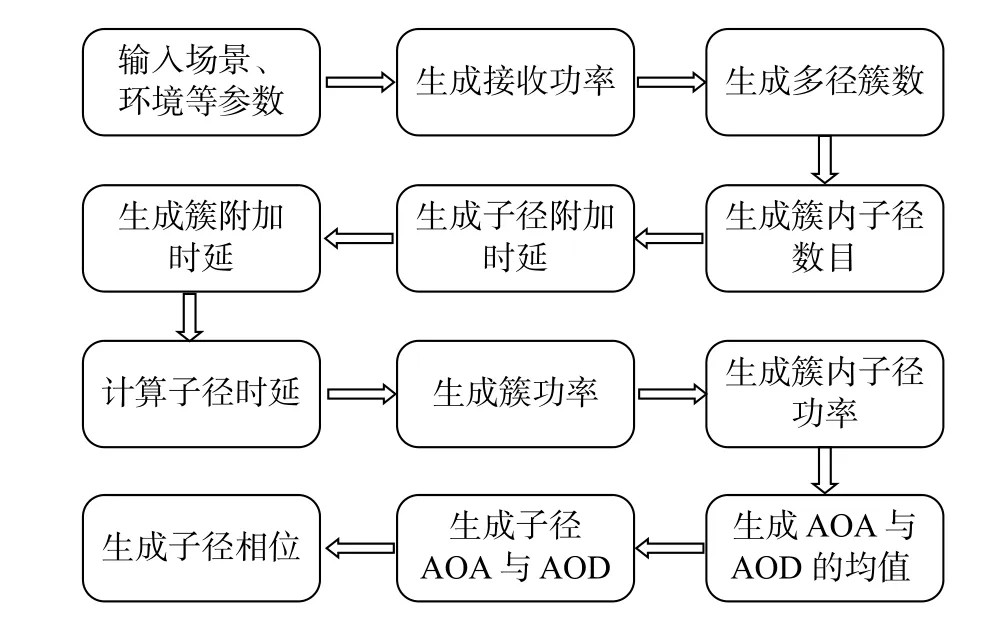
图1 毫米波信道仿真流程图Fig. 1 Flowchart of millimeter wave channel simulation

1)确认输入参数

首先，确定需要模拟的环境类型、场景，以及频率等参数. 其中，环境类型包括城市宏小区(urban macro, UMa)、城市微小区(urban micro, UMi)和农村微小区(rural micro, RMi). 场景包括视距(line-ofsight, LoS)传输和非视距(non-line-of-sight, NLoS)传输. 环境和场景的不同影响路径损耗、阴影衰落以及角度分布类型等参数的设置. 输入参数设置如表1所示.

表1 信道仿真参数Tab. 1 Parameters of channel simulation

2)估计接收功率

接收功率由发射功率、路径损耗和阴影衰落决定，路径损耗取决于T-R之间的距离和路径损耗指数. 路径损耗的计算由下式确定：

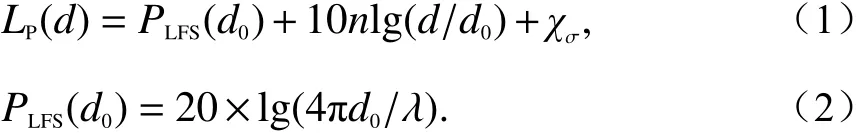
式中：d0=1 m；n是路径损耗指数；χσ是 阴影衰落；λ是载波波长.n与χσ的取值由设置的场景和环境决定.

3)确定多径簇数与簇内子径数

多径簇数在区间[1，10]随机选取，然后根据不同输入场景确定簇内子径数取值，且每个簇内的子径数目不同.

4)确定每条子径的时延

首先确定第n个簇的附加时延 τn， 然后确定第n个簇内第m条子径附加时延 ρm,n，最后将两者与收发机之间传输距离所需要的时间t0相加得到每条子径的时延：

式中：t0=d/c； τn服从指数分布，且第一个簇的附加到达时延为0； ρm,n服从均匀分布.

5)确定每条子径的功率

子径的功率分布服从指数分布，且与子径的时延有关. 首先需要确定每个簇的功率Pn，簇功率的分布也服从指数分布，且满足所有簇的功率之和为接收功率. 然后确定簇内每条子径的功率 Πm,n，且簇内所有子径的功率之和为簇功率.

6)确定每条子径的角度，包括水平到达角 θAOA,m,n、离开角θAOD,m,n与 垂直到达角θZOA,m,n、离开角θZOD,m,n

首先需要确定每个簇内四种角度的平均角度，其中，每个簇内水平角在[0，360°]内随机取值，垂直角满足高斯分布. 在此基础上，生成第n个 簇内第m条MPCs的角度：

式中：angle代表四种角度； θn为 第n个簇的平均角度；Δθn为附加角度分布，且垂直离开角服从拉普拉斯分布，水平到达角、离开角与垂直到达角都服从高斯分布. 表2给出了时延、功率和角度的具体分布情况以及对应参数值的设置.

表2 信道参数分布情况及参数值Tab. 2 Channel parameter distribution and parameter values

7)确定子径的相位

子径的相位φm,n服从均匀分布：

基于以上过程对毫米波信道进行仿真. 图2为26 GHz毫米波信道仿真的功率时延角度谱结果图.从AOA、AOD和时延三个维度可以观察到26 GHz毫米波信道仿真中随机产生了6个多径簇，其中每个簇内子径的数目不同，且时延值小的多径簇功率值整体较大. 产生该结果的原因为：首先，每条子径时延主要由表2中簇附加时延 τn以及子径附加时延ρm,n确定，保证每条子径时延值呈现递减的趋势；其次，对于每条子径功率的分配，由簇功率Pn以及簇内子径功率Πm,n确定；最后，对于每条子径的角度，需要先确定四种角度的平均角度值，然后根据式(4)以及表2中附加角度生成每条子径的角度. 从式(4)可以看出，子径角度基于簇结构生成，因为每条子径的角度由中心角度与附加角度相加得到. 在此基础上，生成了如图2所示的基于簇结构的信道仿真结果图.

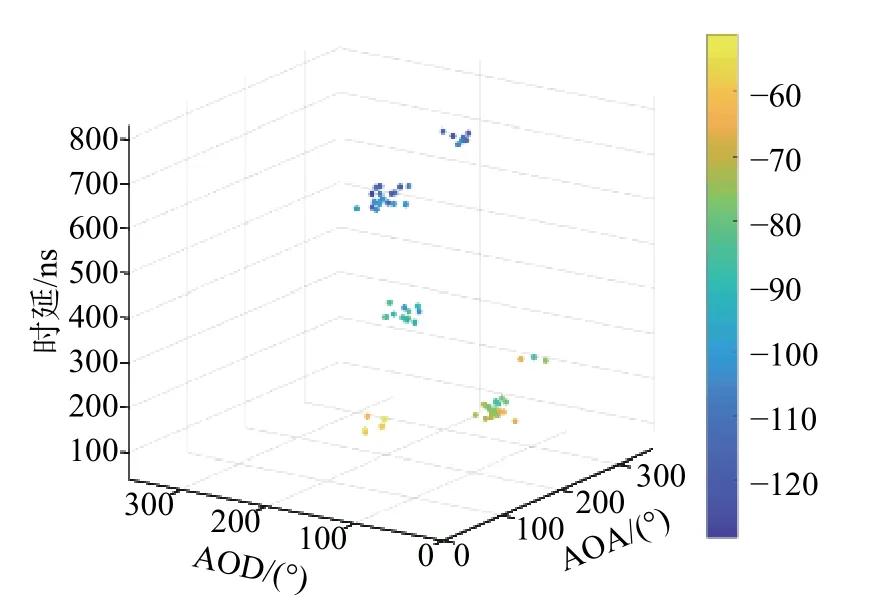
图2 角度时延功率谱仿真结果Fig. 2 Simulation results of angle delay power spectrum

空间一致性描述的是信道中的大尺度参数与小尺度参数随移动距离平滑演进的特性. 本节基于通用的5G毫米波信道模型[15-16]开展仿真和分析，将终端移动轨迹进行分割，针对初始生成的信道参数进行相关性建模，通过建立连续仿真窗口间大尺度参数相关性、窗口间多径簇数目的动态演化以及窗口内小尺度参数的平滑演进实现毫米波时变信道中空间一致性的仿真.

2.1 输入参数与终端轨迹设置

参数设置如下：场景为UMa. 初始环境为LoS.中心频率分别设置为26 GHz、38 GHz与60 GHz. Tx发射功率为40 dBm，位置为(0，0). Tx与Rx的初始距离为10 m. Rx移动距离为40 m，移动速度为1 m/s，在水平面上移动方向为20°. Tx固定且发射天线的高度为10 m，接收天线高度为1.5 m.

仿真中，将移动距离每隔10 m分割为1个仿真窗口，从而进行窗口间信道大尺度参数和仿真窗口内 信道小尺度参数的更新，共划分为4个仿真窗口.

2.2 融合相关性的信道大尺度参数仿真

本节针对信道大尺度参数进行相关性的仿真，大尺度参数包括阴影衰落与信道的LoS/NLoS条件.首先将空间分为网格，每个网格分配具有相关性的大尺度参数，然后根据终端在网格中所处的位置确定大尺度参数. 在此基础上，当终端位置相近时，产生的大尺度参数具有相关性.

在信道仿真中，用二维指数滤波器对独立的阴影衰落与LoS/NLoS条件进行卷积运算，从而建立具有相关性的阴影衰落和LoS/NLoS网格图，其中，二维指数滤波器为

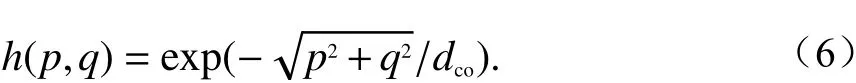
式中：p与q为相对于滤波器中心的坐标；dco是 相关距 离.

2.3 基于马尔可夫链确定窗口间多径簇数目

为了增强连续仿真窗口间信道参数的相关性，更好地实现毫米波动态信道空间一致性的仿真，采用M步3-状态马尔可夫链确定连续仿真窗口内的多径簇数目，从而增强信道仿真的空间一致性. 目前，已有文献通过描述MPCs生灭状态的转移概率来确定MPCs数目的变化，从而实现动态的信道仿真[17-18].本文通过M步3-状态马尔可夫链计算多径簇数目增加与减少的概率，从而确定剩余仿真窗口中多径簇的 数目.

2.3.1M步3-状态马尔可夫链

本文利用3-状态马尔可夫链来刻画不同仿真窗口间的多径簇数目变化的情况. 其中每个状态的定义如下：

·S0—多径簇数目加1；

·S1—多径簇数目减1；

·S2—多径簇数目不变.

图3为3-状态马尔可夫链的状态转移图.

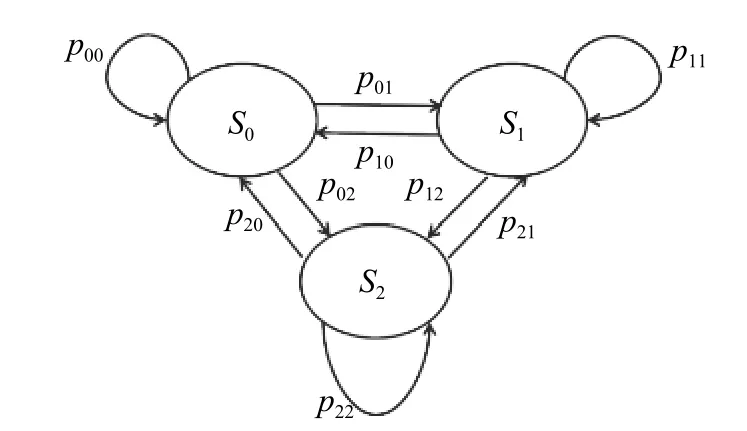
图3 3-状态马尔可夫链的状态转移图Fig. 3 State transition diagram of the 3-state Markov chain

状态间的概率切换由状态转移概率确定：

式中，pij表示从状态Si转 移到状态Sj的 概率.pij满足：

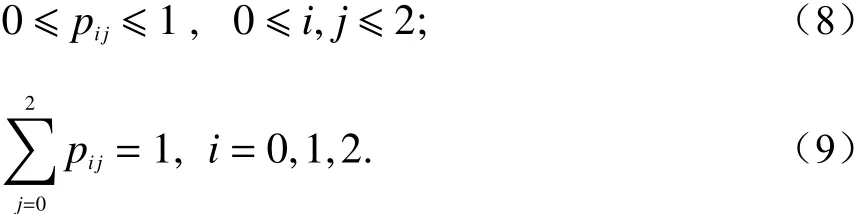
当终端移动时，轨迹被分割为多个仿真窗口. 当终端在连续的仿真窗口间移动时，多径簇数目的变化不只是局限于上述三种变化. 这意味着定义的3-状态马尔可夫链是不够的，可以通过M步马尔可夫链求解多径簇数目，其中，M表示马尔可夫链转移的次数，其取值可以限制连续仿真窗口间多径簇数目变化的范围，进而影响窗口间多径簇数目之间的相关 性，本文设置M=3.

2.3.2 多径簇数增加-减少概率矩阵

根据转移概率矩阵求解多径簇数增加-减少概率矩阵A，其中A中的元素apq代表经过M步状态转移后，多径簇数增加p、 减少q的概率. 矩阵A的维数取决于M，是一个(M+1)×(M+1)的方阵. 由于本文M设置为3，所以多径簇数增加-减少概率矩阵A为

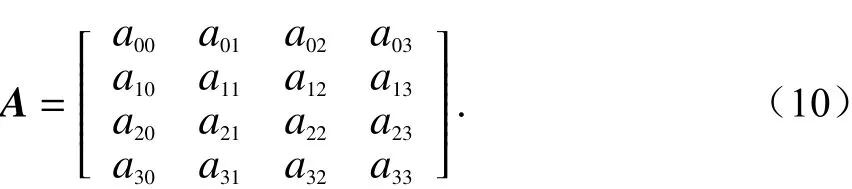
假设状态之间的转移概率都相等，且初始状态为S0，经过三步后，计算矩阵A中元素的数值. 其中，apq与pij具 有一定的联系. 比如：a00表示经过三步马尔可夫变化后，多径簇数增加与减少的数目都为0的概率，只能由S0→S0→S0→S0过程实现，所以a00=在此基础上，得出转移概率矩阵和多径簇数增加-减少概率矩阵如表3所示.

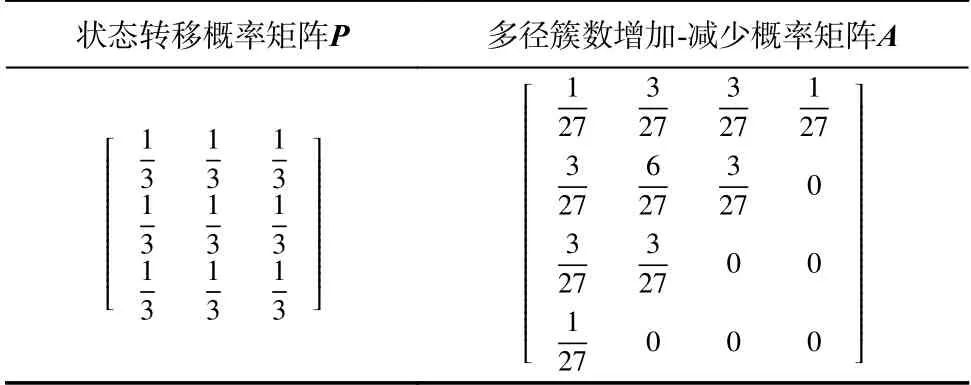
表3 状态转移概率矩阵和多径簇数增加-减少概率矩阵Tab. 3 State transition probability matrix and increasedecrease probability matrix of multiple cluster number

根据得出的多径簇数增加-减少概率矩阵A，按概率值的大小随机选取一个元素值，该元素的下标分别代表多径簇数增加、减少的数目. 定义多径簇增加的数目为LI， 多径簇减少的数目为LR，则下一仿真窗口中多径簇的数目L(t)为

式 中，L(t－1)表示上一仿真窗口中多径簇的数目.

2.4 信道小尺度参数平滑演进

以上两节建立了连续仿真窗口间信道大尺度参数之间的相关性与窗口间多径簇数目的联系，实现了窗口间信道参数的相关性. 本节基于多径的几何分布结构对窗口内MPCs的小尺度参数进行连续更新.

1)子径角度更新

终端移动时，角度变化可以近似表示为

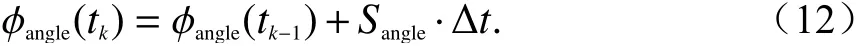
式中：angle为任一种角度；Sangle是角度变化率，其计算过程可以参考文献[16].

2)子径时延更新

利用余弦定律，对时延进行更新：

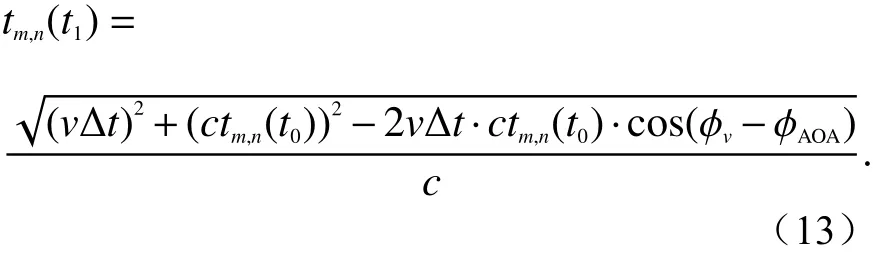
式中，φv是 水平面上的终端移动方向.

3)子径功率更新

根据更新后的时延，重新进行簇功率和子径功率的分配. 首先确定更新后的簇功率，簇功率的分布服从指数分布，且满足更新后所有簇的功率之和为接收功率；然后确定每条子径的功率，且更新簇内所有子径的功率之和为簇功率.

4)子径相位更新

基于路径长度的变化对子径的相位进行更新：

式 中，Δl是路径长度的变化.

2.5 毫米波信道仿真中实现空间一致性的过程

基于以上仿真原理，毫米波时变信道仿真中实现空间一致性的流程图如图4所示. 具体过程归纳如下：

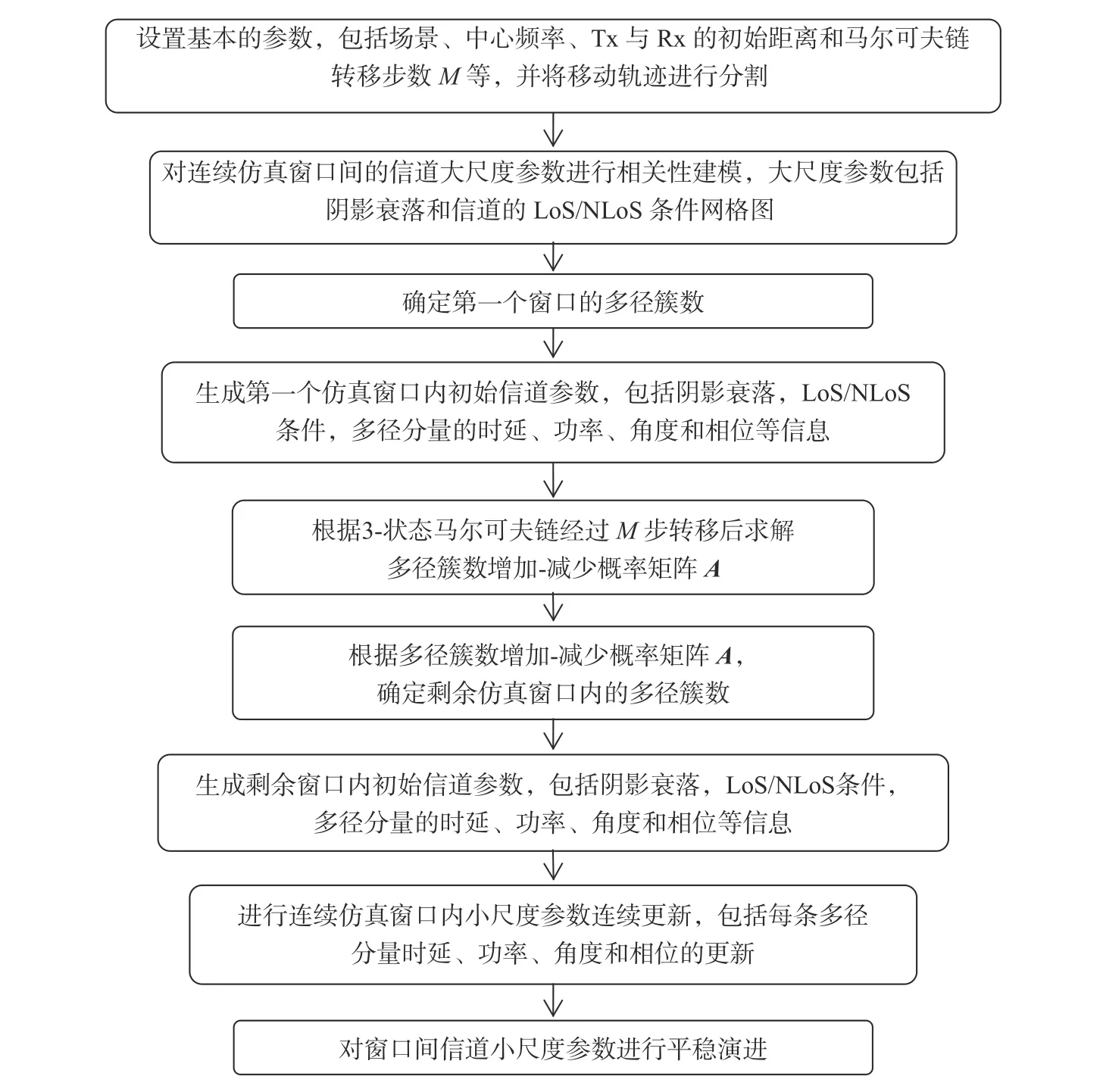
图4 毫米波信道仿真中实现空间一致性的流程图Fig. 4 Flowchart of spatial consistency simulation for millimeter wave channels

1)输入场景、中心频率、Tx与Rx的初始距离和Rx移动速度、马尔可夫链转移步数M等参数，并将移动轨迹进行分割. 具体参数设置见2.1节.

2)对仿真窗口间信道大尺度参数进行相关性建模. 采用二维滤波器对独立值进行卷积运算，从而生成具有相关性的阴影衰落和LoS/NLoS条件网格图.在此基础上，根据终端在网格图中所处的位置，确定各个窗口内的初始信道参数值，且每个窗口内的阴影衰落值与LoS/NLoS条件保持不变，当终端移动到下一窗口时，两者发生改变.

3)确定第一个窗口的多径簇数，在区间[1，10]随机选取一个数作为多径簇数.

4)根据2.1节提供的毫米波信道仿真方法，生成第一个窗口内MPCs的初始信道参数，包括MPCs的时延、功率、角度(AOA、AOD、ZOA、ZOD)和相位信息.

5)根据M步3-状态的马尔可夫链求解多径簇数增加-减少概率矩阵A，其中，M的取值由用户进行输入.

6)根据多径簇数增加-减少概率矩阵A，按概率值的大小随机选取一个元素值，得出剩余窗口的多径簇数目，从而增强连续仿真窗口间信道参数的相关性.

7)生成剩余窗口内的初始信道参数. 根据以上步骤生成的具有相关性的信道大尺度参数以及各个仿真窗口的多径簇数目，依据第1节提供的毫米波信道仿真方法，生成剩余连续仿真窗口的初始信道参数.

8)对每个窗口内的初始信道参数进行更新. 针对窗口内的小尺度参数，基于多径的几何分布结构实现MPCs时延、功率、角度和相位的更新. 具体实现过程见2.4节.

9)针对窗口间信道小尺度参数，基于多径簇的生灭来控制时延、功率、角度和相位的平稳演进. 具体实现过程为：若前一仿真窗口中多径簇的数目大于后一仿真窗口中时延簇的数目，前一窗口的多径簇逐渐消失，并且时延值较大的簇最先消失；若前一仿真窗口中多径簇的数目小于后一仿真窗口中多径簇的数目，后一窗口的多径簇逐渐产生，并且时延值较大的簇最先产生；若两者多径簇的数目相等，前一窗口中多径簇消失的同时新的窗口中多径簇产生.

3.1 毫米波信道空间一致性仿真结果

本节基于第2节提出的毫米波时变信道仿真过程，对空间一致性进行仿真. 表4归纳了信道仿真参数的设置.

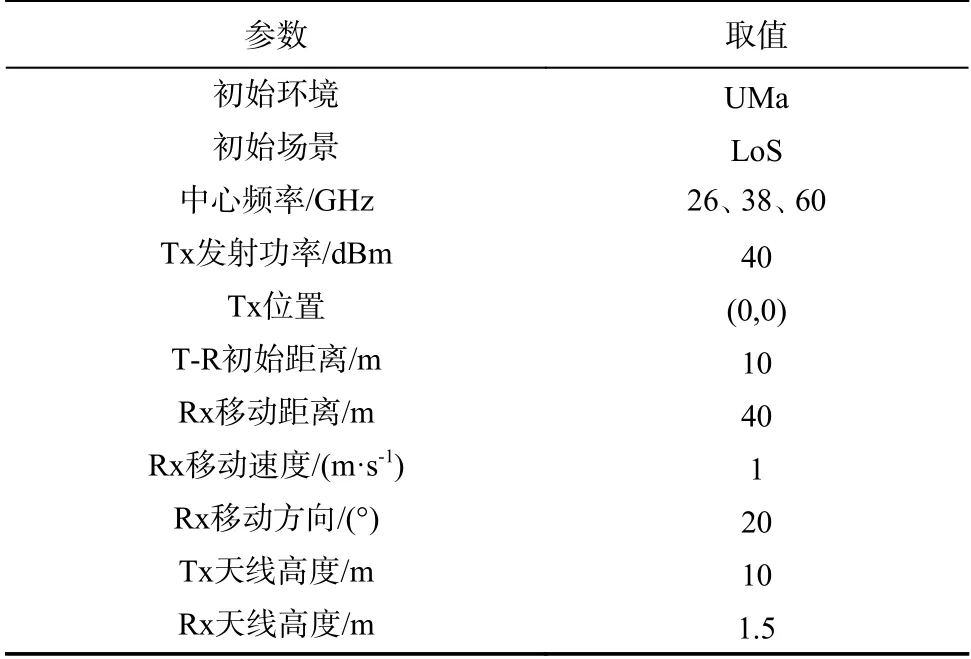
表4 时变信道仿真参数表Tab. 4 Time-varying channel simulation parameters

根据相应仿真参数的设置，建立了Rx移动轨迹仿真示意图，如图5所示. 图中箭头代表Rx的移动方向.

图5 Rx移动轨迹仿真示意图Fig. 5 Simulation diagram of Rx moving track

为了比对凸显空间一致性仿真的必要性，图6为未引入M步3-状态马尔可夫链时随机生成的60 GHz毫米波信道仿真的时延功率谱结果. 可以看出，在连续仿真窗口间生成的多径簇数为4、8、1、1，该值是随机独立生成的，可以通过在仿真过程中输出多径簇数目变量得出，也可以通过观察图中时延簇的个数得出. 在未引入马尔可夫链时，多径簇数目存在从8到1的大幅度跳变的情况. 但是在连续仿真窗口间，Rx移动距离较小，多径簇数等信道参数发生很大变化的概率其实很小，信道参数具有一定的相关性. 因此，未引入马尔可夫链的仿真结果没有准确刻画出毫米波信道中空间一致性的仿真，不符合真实信道下的场景仿真.

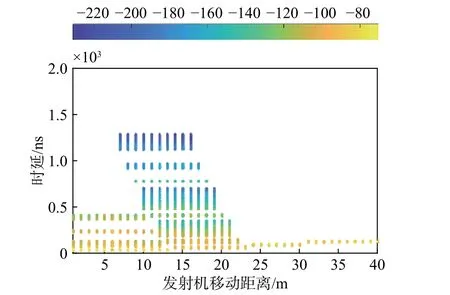
图6 未引入马尔可夫链的信道时延功率谱仿真结果Fig. 6 Simulation results of channel angle delay power spectrum without Markov chain

图7所示为移动情况下满足空间一致性的信道仿真结果示意图. 图(a)～(c)、(d)～(f)和(g)～(i)分别为26 GHz、38 GHz和60 GHz毫米波信道仿真的时延功率谱、AOA角度功率谱与AOD角度功率谱.可以看出：在4个连续仿真窗口中，26 GHz毫米波信道生成多径簇数为6、6、7、7；38 GHz毫米波信道生成的多径簇数为4、2、4、2；60 GHz毫米波信道生成的多径簇数为6、4、3、3. 多径簇数目的变化未发生不合理的大幅度跳变，符合真实时变信道的特征. 在每个仿真窗口内，生成的毫米波信道中MPCs的角度、时延和功率都进行了连续的更新. 在连续仿真窗口间，时延、AOA和AOD发生了变化，这是因为在每个仿真窗口内重新生成了初始的信道参数. 可以看出，所提出的仿真方法实现了信道参数的平滑演进，准确刻画了毫米波信道的空间一致性. 需要指出的是，本文的仿真基于通用的信道仿真器及对应的毫米波信道模型参数[14]生成，该模型本身的准确性已得到了学术界较为广泛的认可. 但是从图7可以看出，38 GHz毫米波信道仿真结果中多径最大功率约为6-65 dB，0 GHz毫米波信道仿真结果中多径最大功率约为-55 dB，而在实际中60 GHz损耗较38 GHz更大. 这是因为虽然该信道仿真产生的60 GHz接收功率较38 GHz更小，但是由于簇数目以及簇内子径数目的不确定性，38 GHz信道仿真产生的簇数目以及簇内子径的数目可能要较60 GHz信道仿真产生更少，因此，会产生60 GHz中多径最大功率比38 GHz中 多径最大功率大的现象.

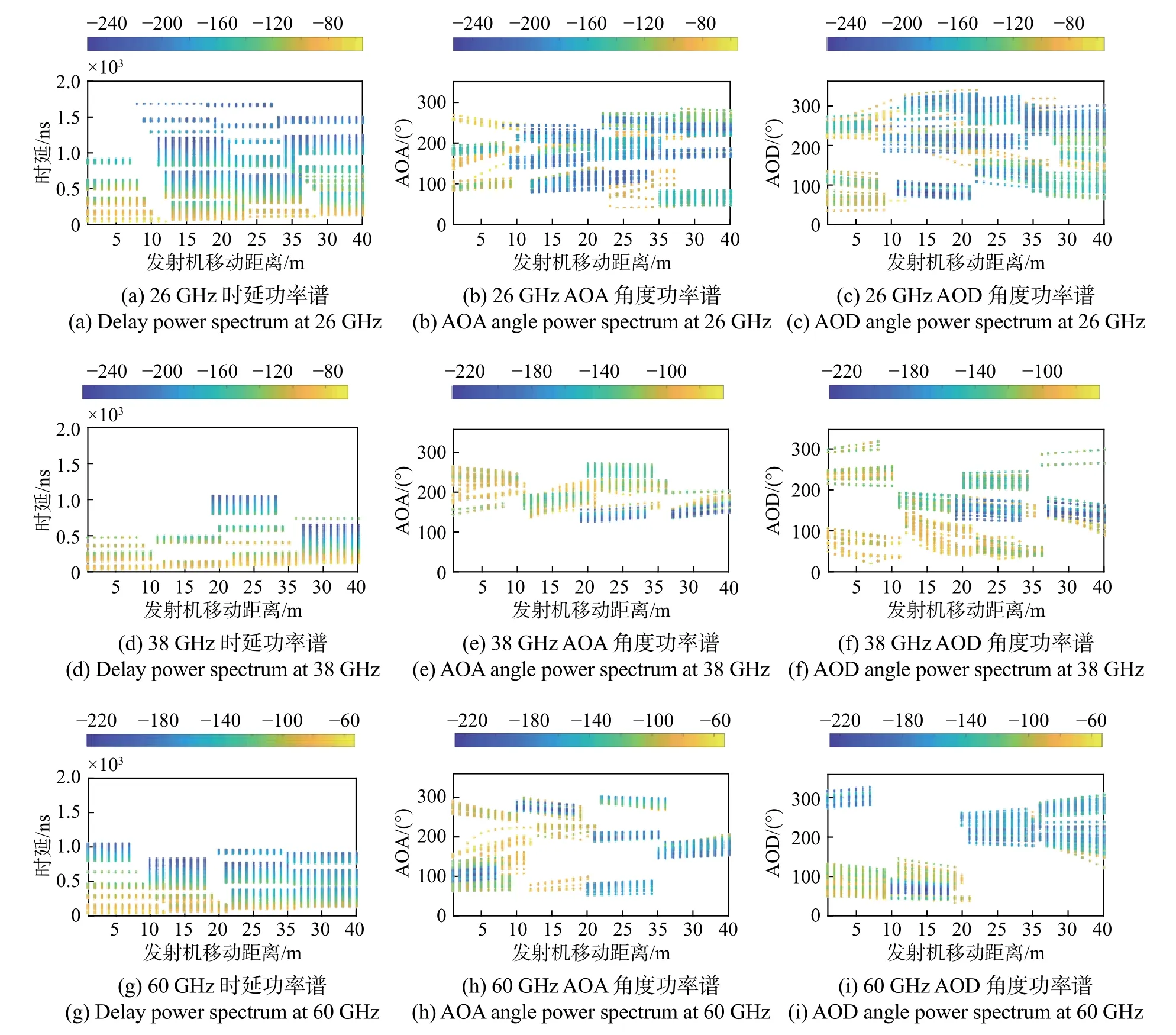
图7 满足空间一致性的毫米波信道仿真结果图Fig. 7 Simulation results of millimeter wave channels satisfying spatial consistency

3.2 空间一致性仿真结果相关性验证

空间一致性表征的是信道参数随移动轨迹的连续性变化，即信道参数在连续仿真窗口间存在着关联性. 而参数的自相关性可描述信道参数在连续仿真窗口间的关联程度，包括连续仿真窗口间信道大尺度参数的自相关性以及窗口内信道小尺度参数的自相关性. 因此，可以通过计算参数的自相关系数验证是否准确实现了空间一致性的仿真. 本节通过计算未引入马尔可夫链与引入马尔可夫链后连续仿真窗口间多径簇数的自相关系数，从而评估马尔可夫链对信道空间一致性仿真结果的影响.

为了消除仿真结果的偶然性，分别对未引入马尔可夫链与引入马尔可夫链后重复开展了50次信道仿真，从而计算不同仿真窗口间多径簇数目序列的自相关系数，且每次仿真时Rx的移动距离均设置为40 m，每个窗口的大小为10 m，即每次仿真都是4个连续仿真窗口. 定义不同的两个仿真窗口间多径簇数目序列的自相关系数为

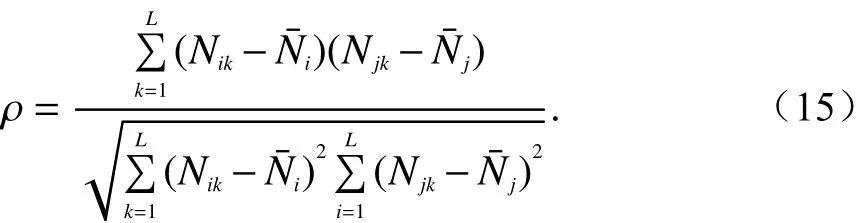
式中：L是仿真次数，本文设置L=50；Nik表示在第k次仿真中第i个仿真窗口内的多径簇数值；Ni表示第i个仿真窗口在50次重复仿真中所产生的多径簇数目序列.

计算得到的多径簇数目序列在不同的两个仿真窗口间的相关系数见表5，其中NiNj表示50次仿真结果中，第i个仿真窗口的多径簇数目序列与第j个仿真窗口的多径簇数目序列之间的关系， ρ1与 ρ2分别表示引入马尔可夫链后与未引入时的相关性系数.

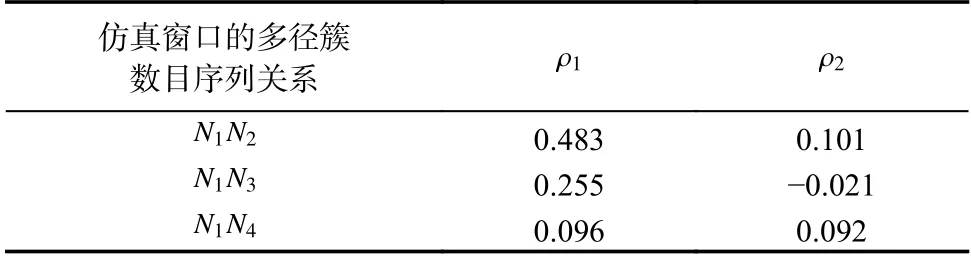
表5 多径簇数目相关性系数Tab. 5 Correlation coefficient of the number of multipath clusters

从表5可以发现：

1)在引入马尔可夫链后，多径簇数目之间的相关性依次减小. 这与马尔可夫链中后一时刻的状态值只与前一时刻有关.

2)在未引入马尔可夫链前，多径簇数目之间的相关性较小，且没有规律. 这是因为不同仿真窗口中多径簇数目是随机独立生成的.

通过引入M步3-状态马尔可夫链，提高了连续仿真窗口间多径簇数目的相关性，增强了仿真窗口之间信道参数的关联程度，提高了信道空间一致性仿真的准确性，使仿真结果更加符合信道实际情况.本文针对现有的实现信道空间一致性仿真的方法，例如NYUSIM信道仿真器，补全了其连续仿真中信道参数相关性缺失这一短板. 但需要指出，由于随机性的存在，相关系数也不应该一味地被提高. 相关系数可以通过状态转移概率矩阵调整，具体的数值应与实际信道测量结果相匹配.

4 结 论

本文开展了26 GHz、38 GHz和60 GHz毫米波信道空间一致性的仿真，通过将移动距离分割成连续仿真窗口来实现信道空间一致性的仿真方法研究.对于连续仿真窗口间的信道大尺度参数，使用滤波器通过卷积运算建立具有相关性的阴影衰落和LoS/NLoS条件；对于窗口间多径簇的数目，使用M步3-状态的马尔可夫链对其进行更新；对于窗口内的信道小尺度参数，基于多径的几何分布结构实现对其状态的连续更新. 最后，通过计算连续仿真窗口间多径簇数目的自相关系数来评估空间一致性仿真的准确性. 结果表明，在引入马尔可夫链之后，提高了信道空间一致性仿真的准确性，解决了已有信道仿真中仿真窗口间信道参数相关性缺失的问题. 未来的研究中，针对大尺度参数可以建立不同参数之间的相关性，如莱斯K因子、均方根时延扩展和角度扩展等系数的相关性；针对小尺度参数，可以通过统计连续仿真窗口间多径簇的生灭概率与簇内MPCs的生灭概率，从而进一步提高毫米波信道仿真时空间一致性仿真的准确度.