基于空间递推的毫米波信道一致性仿真算法研究

崔昊 钱肇钧 富子豪 杜飞 刘永胜 耿绥燕 赵雄文

（1.华北电力大学电气与电子工程学院，北京 102206；2.国家无线电监测中心，北京 100037；3.中国电波传播研究所电波环境特性及模化技术重点实验室，青岛 266107）

引 言

5G系统的公网建设正在稳步推进，为满足5G超高速率的传输需求，毫米波通信技术被应用于5G通信系统中. 毫米波频段拥有几个GHz的带宽资源，被认为是B5G (beyond 5G)及6G的关键技术. 毫米波频段的信道建模及仿真工作成为了各国科研机构、大学和企业无线通信研究的重点. 其中，26 GHz及28 GHz频段是毫米波频段中的重点频段，受到了国内外研究者的广泛关注[1-3]. 第三代合作伙伴计划(The 3rd Generation Partnership Project, 3GPP)及国际电 信 联 盟(International Telecommunication Union,ITU)已经初步完成了5G信道模型的标准化工作[4-5].然而，对于毫米波信道仿真，标准化文件中基于统计分析的仿真方法已经不能满足要求. 毫米波无线信号具有多径稀疏性，多径生灭对信道影响明显；5G网络主要布设于用户热点地区，信道中存在大量移动散射体，例如行人、车辆等，使得信道呈现快时变特性. 而传统的基于几何的随机信道模型(geometrybased stochastic channel model, GSCM) 基于广义平稳假设，包括3GPP提出的空间信道模型(spatial channel model, SCM)[6]、扩展的空间信道模型(SCM extension,SCME)[7]、无线世界创新无线电(wireless world initiative new radio, WINNER)、WINNER II[8]和WINNER+[9]等，在仿真过程中有着相邻用户信道参数不连续的问题，迫切需要开展毫米波时变信道建模及仿真方法的研究.

时变信道仿真要求大尺度参数(large-scale parameter, LSP)及小尺度参数(small-scale parameter,SSP)均具备空间一致性，即信道的LSP与SSP随着空间移动进行连续更新. 时变信道仿真的一种常用方法是先生成空间一致性LSP，再根据LSP生成空间一致性SSP. WINNER II[8]标准化文件中给出了一种空间一致性LSP生成算法(以下简称WINNER II算法). 该算法应用广泛，3GPP TR38.901[10]、德国Fraunhofer HHI实验室提出的准确定性无线信道仿 真 器(quasi-deterministic radio channel generator,QuaDRiGa)[11]及纽约大学提出的NYUSIM[12]信道仿真器的LSP生成算法中均使用WINNER II算法.

本文提出了一种新的LSP生成算法，该算法基于一种递推思想，在空间中依次生成信道LSP，以下简称空间递推算法(spatial recursion algorithm, SRA).基于国家体育场(以下简称鸟巢)28 GHz信道测量数据开展了信道仿真工作，并将SRA的仿真结果与WINNER II算法的仿真结果进行对比. 根据两者的仿真结果分别计算信道LSP及空间一致性参数，并分别与实测得到的信道LSP及预设的空间一致性参数对比，验证了SRA仿真的准确性.

1 鸟巢信道测量场景

在28 GHz频段下进行喇叭天线(horn antenna)旋转测量以及虚拟大规模天线测量. 喇叭天线旋转测量时，发射端使用全向天线，接收端使用喇叭天线.接收端喇叭天线在水平面以及垂直面进行旋转扫描，水平面扫描步长为5°，扫描范围为0°～360°；垂直面扫描步长为5°，视距(line-of-sight, LoS)扫描范围为-5°～10°，非视距(non-line-of-sight, NLoS)扫描范围为-5°～5°. 虚拟大规模天线测量时，发射端使用全向天线，接收端利用水平平移电机将8单元均匀线性阵列 (8 elements uniform linear array, ULA-8) 天线平移16次形成相互独立的8组虚拟ULA-16. ULA-8每次水平平移距离为半波长，即5.36 mm. 测量系统具体参数见表1.

表1 测量系统参数Tab. 1 Measurement system parameters

图1 (a)、 (b)分别为LoS与NLoS场景下的信道测量场景，图2(a)、(b)为其测量方案示意图. 图2(a)LoS场景中：三角形表示发射天线Tx，位于观众席台阶上；接收天线Rx位于运动场中；ULA测量位置用空心圆表示，编号为Rx1至Rx11，间隔5 m；喇叭天线测量位置用实心圆表示，编号为Rx1至Rx17，其中Rx1至Rx12间隔5 m，Rx12至Rx17间隔10 m；ULA Rx6正对发射天线. 图2(b) NLoS场景位于体育场的观众通道，Rx1至Rx10间隔5 m，其中Rx1至Rx6为ULA测量点，Rx1至Rx10为喇叭天线测量点. 环境中的散射体主要为体育场中的座椅以及立柱、墙壁等.

图1 信道测量场景Fig. 1 Channel measurement scenarios

图2 信道测量场景示意图Fig. 2 Maps of measurement scenarios

2 信道参数建模及分析

在无线信道研究中，通常用信道参数描述信道特征. 因此在信道测量后，通过空间交替广义期望最大 化 (space-alternative generalized expectationmaximization, SAGE)算法[13]从信道冲激响应(channel impulse response, CIR)中提取信道SSP，即多径分量(multipath components, MPCs)，从而计算并分析路径损 耗(path loss, PL)、阴 影 衰 落(shadow fading, SF)、时延扩展(delay spread, DS)、角度扩展(angle spread,AS)等信道LSP[14].

喇叭天线增益较高，可以捕捉到更丰富的无线信号，因此通常使用喇叭天线测得数据进行PL建模.PL分为全向性路损和方向性路损，其中全向性路损使用各个接收方向接收功率总和计算，而方向性路损则只考虑最强功率进行计算. 本文因鸟巢环境较为空旷，多径角度域弥散较小，选取方向性路损进行拟合. PL建模结果如图3所示， σ 为SF标准差. 可以看出，28 GHz下的固定截距(close-in, CI)模型在LoS场景中与自由空间损耗模型拟合良好，而NLoS场景中PL远大于LoS场景，这是由于NLoS场景下的散射环境更加复杂导致的.

图3 PL示意图Fig. 3 Path loss diagram

因DS与水平到达角角度扩展(azimuth angle spread of arrival, AASA)均服从对数正态分布，因此在统计分析时均采用以10为底的对数形式[10]. 为避免角度周期性引起的干扰，本文中AASA采用循环AS. 图4 (a)、(b)分别为DS与AASA的累积分布函数(cumulative distribution function, CDF)示意图. 图中使用高斯分布分别对LoS及NLoS场景下的DS与AASA的CDF进行拟合，拟合结果良好. 由于LoS场景下视距径功率极强，多径色散相对较弱，因此LoS场景中的DS与AASA均小于NLoS场景，与实际情况相符.

图4 LSP CDF示意图Fig. 4 CDF of LSP

本次测量的鸟巢场景与3GPP TR38.901中的城市微蜂窝(urban microcell, UMi)场景较为接近. 表2为LoS和NLoS场景下的28 GHz鸟巢与3GPP TR38.901 UMi场景信道参数. 可以看出，鸟巢场景中的PL指数n以及SF标准差 σXS与3GPP TR38.901 UMi场景中的参数吻合较好，仅在LoS场景下的 σXS相差较大.这是由于LoS场景选取体育场观众席，其环境相比典型场景更为空旷，多径较少引起标准差减小. 与3GPP TR38.901 UMi场景相比，鸟巢中间为跑道与足球场，面积大且空旷；跑道旁边的观众席虽有大量的表面光滑的座椅，但桌椅高度较低，远低于发射天线高度，只有少数多径经过座椅到达接收机，导致体育场场景中的DS与AASA均小于3GPP TR38.901 UMi场景.

表2 两种场景下鸟巢与3GPP TR38.901 UMi场景信道参数对比Tab. 2 Comparison of channel parameters between the Bird’s Nest and 3GPP TR38.901 UMi in two scenarios

3 信道模型及空间一致性

在基于几何统计的信道模型中，信道的空间一致性体现在信道参数的连续性之中. 本节首先给出鸟巢信道的多径传输模型，之后具体介绍无线信道LSP的空间一致性相关概念，包括自相关特性与互相关特性.

3.1 无线信道多径传输模型

在鸟巢信道测量中，信道测量的发射端使用全向天线，其可向各个方向以相同功率辐射电磁信号；在接收端可使用阵列天线，以分辨来自不同方向的无线信号.

假设电磁波从全向天线发出，经L条不同的路径到达由M个阵元构成的阵列天线，构成单入多出(single-input multiple-output, SIMO)系统. 将发射信号定义为u(t)，则在接收端接收到的第l条路径的信号可表示为[14]

式中， ρl=[τl,θl,φl,vl,αl]是第l条多径的参数集，集合中的参数依次表示时延、垂直到达角、水平到达角、多普勒频移和复幅值；c(θl,φl)为导向矢量，与天线结构及天线方向图有关. 若M根天线的位置分别为r1,r2,···,r M， 则c(θ,φ)公式如下：

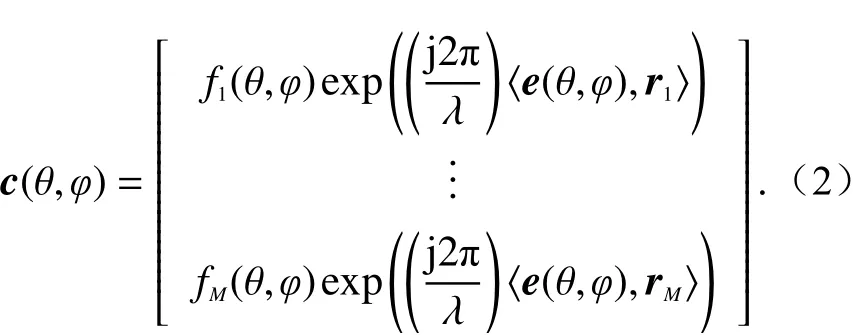
式中：fm(θ,φ)表示第m个天线阵元的复方向图；λ表示载波波长； 〈·〉表示内积运算；e(θ,φ)是球坐标单位方向矢量，

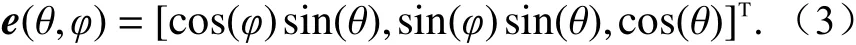
接收阵列天线的响应矩阵形式如下：

式 中：N0为正的常量；N(t)为M维高斯白噪声.

3.2 无线信道空间一致性

空间一致性是时变信道仿真中的重要特性. 对于LSP，空间一致性具体体现在参数的空间自相关特性与空间互相关特性中[15].

信道参数的空间自相关特性指的是同一空间两条链路中同一参数的相关性随距离变化的特性，通常使用皮尔森(pearson)相关系数度量参数相关性，自相关系数ρX(d)公式如下：

4 SRA

假设某场景的空间中存在由一台发射机与K台接收机组成的K条链路，每条链路存在M个LSP，算法具体步骤如下：

1)在场景中恰当地建立坐标系，其中坐标系单位长度1表示实际场景中1 m. 输入K台接收机位置pk=(xk,yk)(k=1,2,···,K)，输入M维LSP均值 μm与标准 差 σm(m=1,2,···,M)，输 入 参 数 相 关 矩 阵ρ=(ρmn)M×M(m,n=1,2,···,M)，其中 矩 阵 元素 ρmn为 参 数m与n的相关系数. 初始化i=1以记录算法迭代次数，初始化集合P={1,2,···,K}以记录未生成参数的链路编号，初始化参数D=0以记录算法迭代过程中接收机总间隔. 根据仿真环境恰当设定阈值dth.

2)开始第1次迭代. 在K条链路中随机选取链路k1作为初始链路，根据M维正态分布生成该链路的M维LSP集 ξM(xk1,yk1).M维正态分布的概率密度函数公式如下：

图5 SRA算法流程图Fig. 5 Algorithm flow chart of SRA

5 信道仿真结果及分析

本节分别使用WINNER II算法及SRA对鸟巢28 GHz信道进行仿真，综合对比两算法的仿真结果及信道建模结果，分析SRA的仿真精度及空间一致性.

WINNER II算法首先将各参数映射为标准正态分布变量，再使用空间滤波器和相关矩阵依次为该变量添加空间自相关与互相关特性，最后将变量反映射为原参数，得到具有空间一致性的参数集. 与WINNER II算法相比，SRA通过多维正态分布直接获得参数互相关，无需单独生成参数互相关特性，仿真步骤更加简单.

WINNER II算法仿真采用QuaDRiGa仿真平台[11]，QuaDRiGa仿真平台基于QuaDRiGa模型改进而来[16]，可支持时变信道仿真. 在LSP生成过程中，QuaDRiGa仿真平台基本沿用了WINNER II模型的算法，因此该平台生成的LSP即可视为WINNER II算法的生成结果.

本文以存在自相关与互相关特性的参数DS、AASA、SF为例，具体分析本文提出的SRA与WINNER II算法的优劣. 仿真环境设置如下：发射机位于原点，高10 m；共设置2 001个接收机，接收机位于同一条直线上，其坐标起止点分别为 (22.15, -500) 和(22.15, 500)，坐标轴长度单位1代表1 m，两相邻接收机间距为0.5 m. 本次仿真设置的接收机个数远大于测量点数，因此可认为结果不存在统计偏差. 仿真参数完全按照LoS场景的实测参数进行设置. DS、AASA、SF的相关距离及互相关系数根据3GPP TR38.901中的UMi场景进行设置，取dth=18 m.

SRA与WINNER II算法仿真得到的LSP CDF仿真结果如图6所示. 从图6可知，与WINNER II算法结果相比，SRA的结果与实测场景更加吻合. 这是由于WINNER II算法中添加的自相关与互相关特性的步骤破坏了参数集的标准正态分布，而之后的逆映射步骤基于参数集的标准正态分布假设，因此非标准正态分布的参数集在逆映射之后得到的LSP精度较差.

图6 两种算法得到的 LSP CDF仿真结果Fig. 6 LSP CDF simulation of the 2 algorithms

根据式(5)及式(6)，计算仿真结果的自相关及互相关系数，并计算各参数的自相关距离，所得的空间一致性参数见表3. 可以看出，WINNER II算法与SRA均能根据预设参数良好地实现参数的自相关与互相关特性，从而完成空间一致性仿真. 与WINNER II算法相比，SRA生成的LSP更接近实测数据，仿真精度更高.

表3 信道仿真空间一致性参数Tab. 3 Spatial consistency parameters of channel simulation

6 结 论

本文提出了一种被称为SRA的5G毫米波空间一致性LSP生成算法. 该算法根据特定的递推算法，用多维正态分布依次生成各仿真点的参数，以实现空间自相关与互相关特性. 并根据鸟巢28 GHz信道测量数据开展了信道仿真工作，与传统的WINNER II算法进行了对比. 结果显示，两种算法均能良好地完成信道空间一致性仿真. 相比于WINNER II算法，SRA的结果与信道测量数据吻合更好，仿真精度更高，且SRA无需单独进行空间互相关特性的生成，仿真步骤更为简单. SRA可为以后的空间一致性LSP生成算法提供一种新的思路，对5G毫米波时变信道仿真有着重要意义. 目前该算法仅用于链路级仿真，未来将继续研究其在系统级仿真中的应用. 此外，算法中参数的空间自相关特性生成方法仍存在优化空间，后续将进一步进行研究.