敞口钢包转运过程中钢水温降规律的研究

叶成立 金 杨

(二重(德阳)重型装备有限公司，四川618000)

在铸件和钢锭的生产中，一般钢包炉与浇注工位距离较远，而且常有多包顺序合浇的情况，所以钢水存在转运过程，该过程用时长达20～60 min。而高质量的铸件和铸锭对浇注时钢水的温度有严格的要求，所以钢水的温降就极其重要，只有掌握钢水温降的规律，才能根据浇注温度控制出钢温度。

1 钢包传热数学模型建立

钢水冶炼完成以后，停电开出，吊运至浇注工位。在这个过程中，将钢包作为一个整体考虑，可以认为是一个无内热源散热的过程，散热主要是对流散热和辐射散热。为了计算简便，作如下简化：

(1)任何时刻钢包内钢水温度是均匀的。

(2)包壁和包底表面的温度也是均匀的，并在转运过程中保持不变，维持出钢时的温度。

(3)不考虑包壁耐火层之间的接触热阻，认为各层耐材之间紧密结合。

(4)钢水表面覆盖的炉渣表面各处温度一致，且存在一个冷却层；冷却层以下的渣子认为和钢水温度相等。

简化以后，钢包的尺寸及钢包传热模型如图1所示，散热主要是对流散热Ec和辐射散热Er。

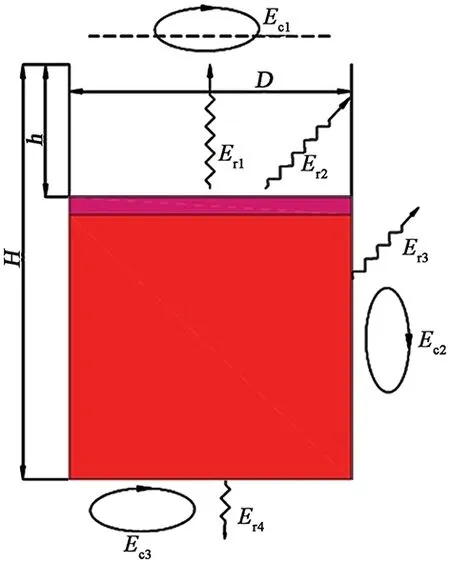
图1 钢包传热模型示意图Figure 1 Schematic diagram of ladle heat transfer model

于是，总散热量E有：

E=ΣEc+ΣEr=Ec1+Ec2+Ec3+Er1+Er2+Er3+Er4

(1)

2 钢包传热模型的求解

2.1 对流传热计算

由于钢包在吊运过程中速度很慢，所以可以认为是和空气自然对流散热。根据牛顿冷却公式，对流散热的热流密度如下所示：

qc=λ(Tb-Te)

(2)

式中，qc为对流散热的热流密度；λ为换热系数；Tb、Te分别为包壁和环境温度。

其中，换热系数λ为未知，又根据努塞尔Nu准数关系：

Nu=λL/k

(3)

Nu=f(Gr,Pr)

(4)

式中，Nu为努塞尔准数；k为对流边界层导热系数；L为对流特征尺寸；Gr为格拉晓夫准数；Pr为普朗特准数。

自然对流传热的相关实验关联式见表1。

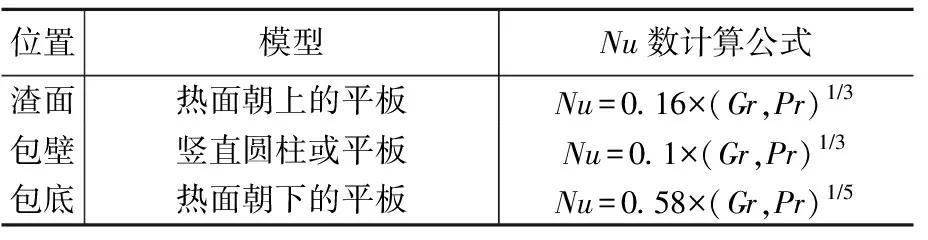
表1 自然对流条件下不同位置努塞尔准数Nu实验关联式[1]Table 1 Experimental correlations ofNusselt's quasi-number Nu at different positionsunder natural convection conditions

综上，对流散热ΣEc为：

ΣEc=Σλi·ΔTi·Fi

(5)

2.2 辐射传热计算

2.2.1 包壁和包底辐射散热计算

对于包壁和包底，简化之后认为温度不变，且认为壁面辐射全部被大气空间吸收。所以根据史蒂芬-玻尔兹曼定律(四次方定律)，辐射散热见式(6)。

(6)

式中，F为包壁辐射面积，ε为黑度值，一般氧化的钢或铁为0.8；σ为黑体辐射系数，5.67 W/(m2·K4)；Tb、Te分别为包壁和环境温度。

2.2.2 渣面辐射散热计算

渣面辐射散热比较复杂，这是因为：

(1)渣面辐射分为两部分，一部分被大气吸收，一部分被包壁吸收。而且渣面距离包口位置不同，辐射的角系数不同。

(2)渣面在出钢以后，渣面表面冷却层温度急剧下降，造成辐射散热能力发生巨大变化。

所以，对于渣面辐射散热，必须分两部分考虑。

对于渣面向上方包口空气的散热有：

(7)

对于渣面向钢包内壁的散热，根据灰体辐射换热则有：

(8)

式中，F为包壁辐射面积，φ为辐射角系数，ε为黑度值，一般氧化的钢或铁为0.8；σ为黑体辐射系数，5.67 W/(m2·K4)；Tz、Te、Tn分别为渣面、环境以及内壁的温度。

(1)渣面辐射角系数的确定

渣面辐射模型如图2所示，渣面和包口直径为D，距离为h；包口面积为F1，包壁面积为F2，渣面面积为F3。

由于包壁是耐火材料，导热系数较低，可以认为是不导热，那么其渣面对包口的辐射角系数满足相等且平行圆盘之间的辐射角系数[2]。图3是辐射角系数φ3,1的测量值和拟合值。

图2 钢包渣面向空气辐射示意图Figure 2 Schematic diagram of air radiation of ladle slag图3 相等且平行的圆盘间角系数[2]Figure 3 Equal and parallel angle coefficient between discs

因为不同的钢包、不同的钢水量会对角系数有影响，为了方便连续计算，对角系数进行拟合，拟合公式如式(9)所示。

φ3,1=-0.002(D/h)4+0.033(D/h)3-0.210(D/h)2+

0.615(D/h)+0.048

(9)

(2)渣面温度变化的确定

出钢以后，渣面温度急剧下降，表面一定厚度的渣层由红亮的液态迅速变为红黑色的凝固态渣壳，之后温度缓慢变化，可以对钢水起保温作用。

根据渣面瞬态迭代法，可以计算渣面温度的变化，如图4所示。

(10)

式中，Ti+1、Ti分别为渣面冷却层i、i+1时刻的温度；Qir、Qic分别为i时刻辐射出的热量、钢水向冷却层传导的热量；δ为渣面冷却层的厚度，为1～2 cm。

由图4可以发现，开始时渣面温度迅速降低；当时间超过10 min以后，温度开始缓慢降低，基本稳定。实际测量结果显示渣面温度在1000～1100℃左右，与该公式吻合较好。

2.3 钢水温降计算

由于钢包在吊运过程中，无能量输入，所以散失的热量造成钢水和熔渣温度的降低，温降ΔT如式(11)所示：

Et=(Mmcpm+Mscps)ΔT

(11)

式中，t为时间；Mm、Ms分别为钢水和渣子的重量，kg；cpm、cps分别为钢水和渣子的比热容。

3 计算结果与分析

3.1 边界条件的测量与选用

通过求解过程可知，需要知道钢包尺寸、包壁及包底的温度、钢水量、渣量以及各种相关物性参数。

我公司有A、B、C、D共4种常用类型的钢包，其直径相等，高度不同。采用手提式测温枪对出钢后的包壁和包底测温，统计后取平均数，见表2。钢水及熔渣的物性参数见表3。

图4 渣面温度随时间变化Figure 4 Changes of slag surface temperatures with time

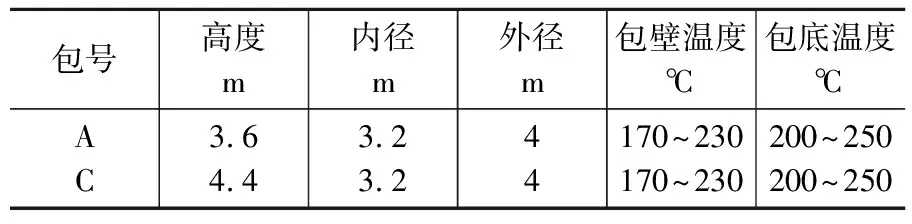
表2 钢包相关参数Table 2 Related parameters of ladle

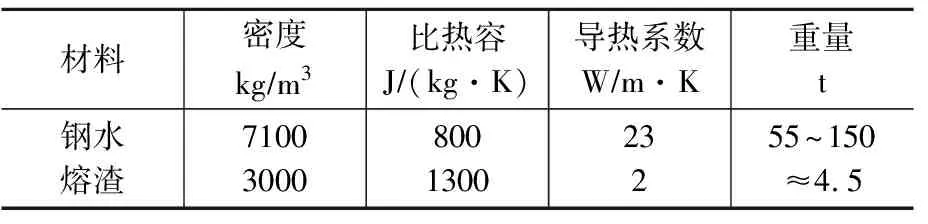
表3 钢水和熔渣的物性参数Table 3 Physical parameters of molten steel and slag

另外，对于对流散热计算中空气的各项参数见参考文献[1]，本文不再一一列出。

3.2 钢水温降计算结果

3.2.1 钢水的降温速度

图5分别为A包和C包不同钢水量时钢水降温速度与时间的关系。从图中可以看出，刚开始时，钢水温度降低速度很快，当时间大于10 min，钢水温降趋于稳定；同一个钢包，钢水越少，降温速度越快。

从图5可以读出，当钢水分别为55 t和95 t时，稳定时的温降速度分别为约1℃/min和0.65℃/min。钢水量与温降速度不是严格成反比，这是因为稳定以后二者总散热量不同，钢水量较少的时候，渣面向外辐射的角系数小，相应的渣面辐射散热会变小。

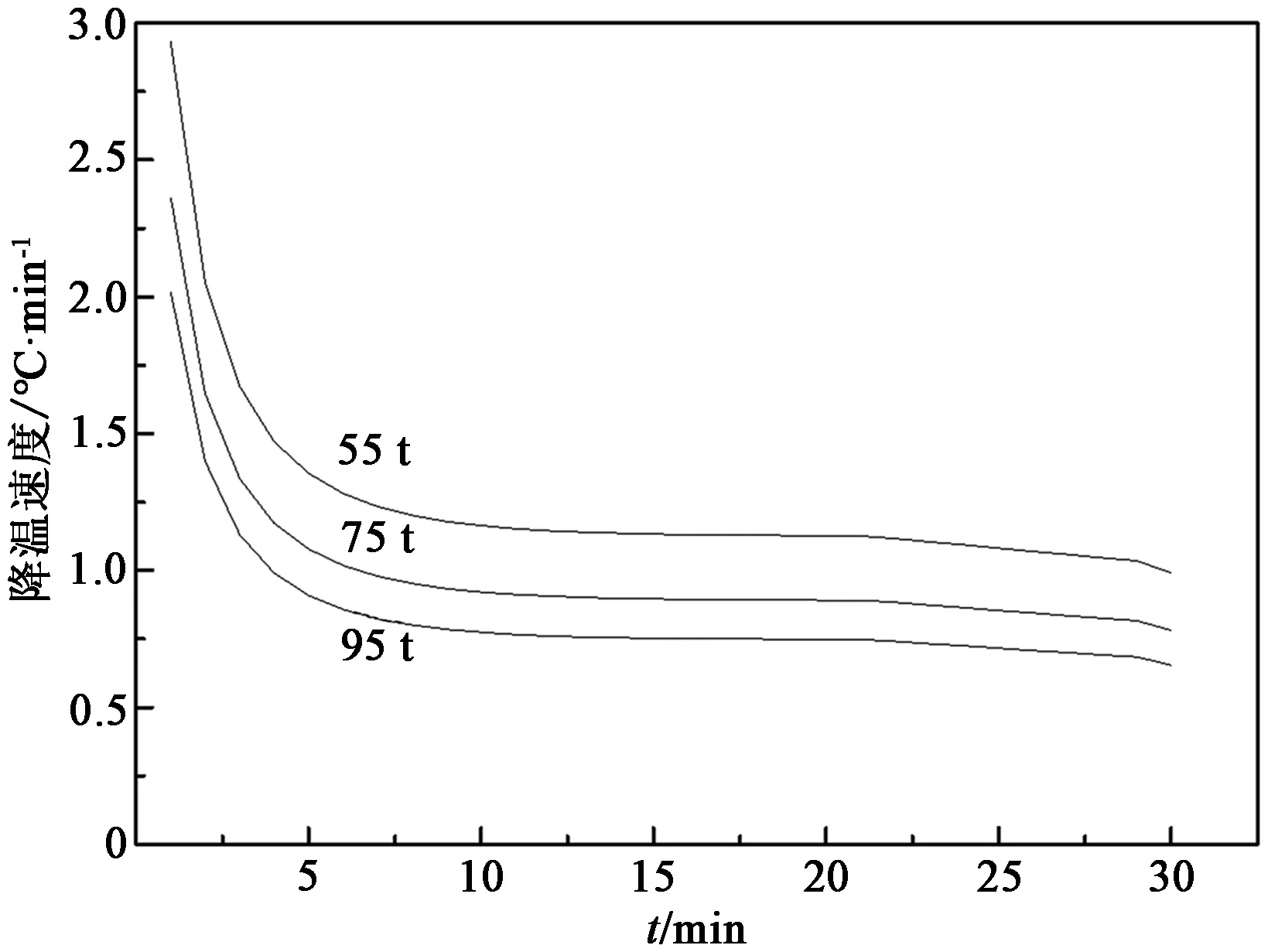
(a)A包(b)C包图5 不同钢水量的降温速度Figure 5 Cooling rate of different molten steel volume

3.2.2 钢水总温降影响因素

图6是A包和C包在不同钢水量时钢水总温降与时间的关系。可以发现，相同钢包较大吨位和较小吨位的钢水总温降在30 min时相差超过10℃。

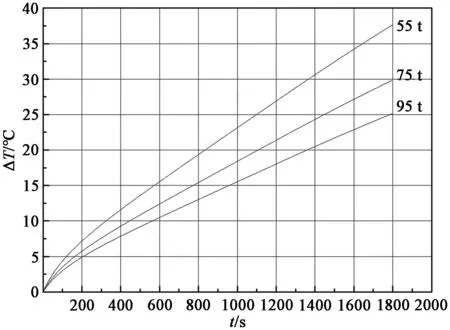
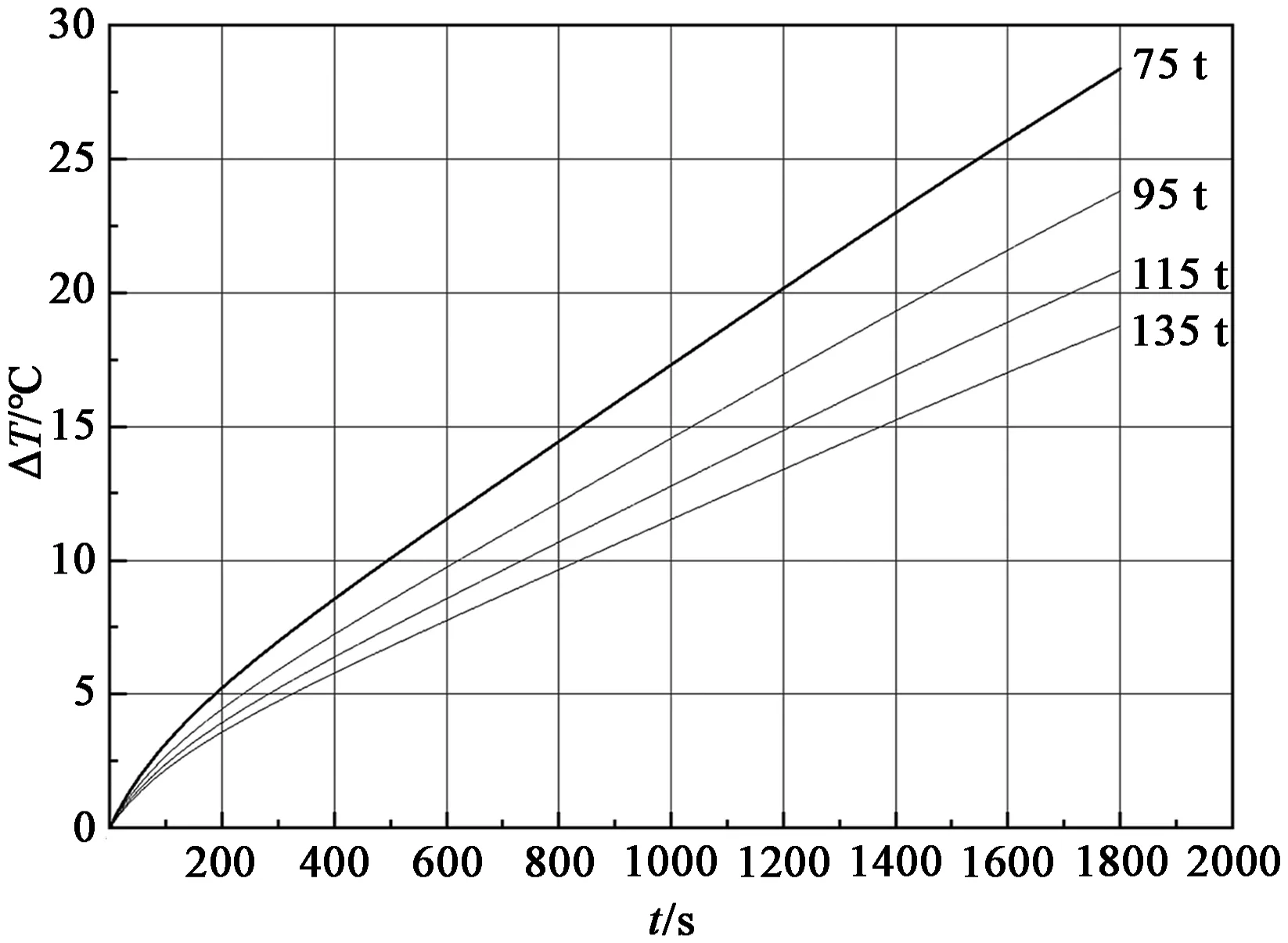
(a)A包(b)C包图6 不同钢水量时的钢水总温降与时间的关系Figure 6 Relationship between total temperature dropand time of molten steel with different water quantity

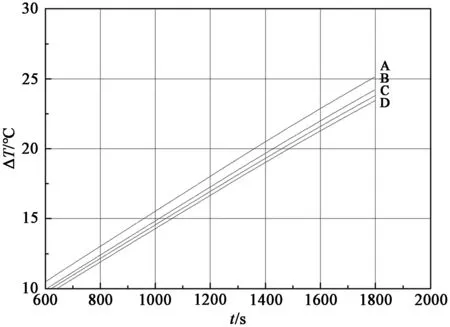
(a)不同钢包95 t钢水(b)不同钢包135 t钢水图7 相同钢水量时的钢水总温降与时间的关系Figure 7 Relationship between total temperature dropand time of molten steel with the same amount of water

图7是A包和C包在相同钢水量时钢水总温降与时间的关系。可以发现不同钢包在盛有相同钢水量时，30 min后钢水总温降相差小于3℃。

图8 钢包散热方式占总散热比例Figure 8 The proportion of ladle heat dissipation methodin total heat dissipation

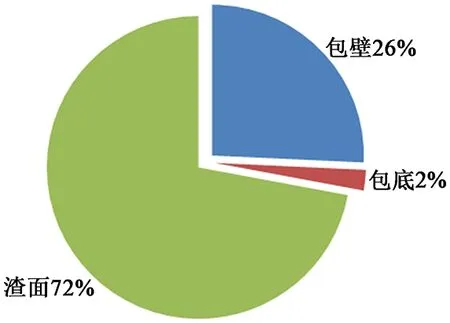
图9 钢包散热部位占总散热比例Figure 9 The proportion of the heat dissipation partof the ladle in the total heat dissipation

3.2.3 钢包不同位置散热贡献

图8是不同散热方式占总散热的比列，可以发现辐射散热是主要的散热方式。图9是钢包不同散热部位占总散热的比列，渣面是主要的散热部位，所以采取措施减少渣面散热是降低钢水温降最有效的方法。

4 结论

(1)本文建立了敞口钢包在转运过程的数学模型，在合适的简化和边界条件下，可以准确地计算钢包内钢水的温度变化。

(2)前期钢包内钢水温降速度较大，随后趋于稳定；相同钢包内钢水的温降速度随钢水量增加而减小。

(3)相同钢包内不同钢水量时钢水总温降相差较大，相同的钢水量在不同钢包内的钢水总温降相差较小。

(4)钢包散热的主要方式是辐射散热，渣面是主要的散热部位。