基于能量耗散的Q460焊接接头S-N曲线快速预测
魏巍, 邹丽, 杨鑫华
(1.大连交通大学,辽宁 大连 116028;2.辽宁省轨道交通装备焊接与可靠性重点实验室,辽宁 大连 116028)
0 前言
Q460耐候钢由于强度高、耐候性好等优点,在铁路货车车体生产制造领域有广泛的应用。其焊接结构在服役过程中承载着由车体产生的各类循环载荷,且因焊缝处的几何、组织不连续性等特点[1-2],易于在焊趾处率先开裂而导致结构疲劳破坏。因此,关于铁路货车Q460焊接结构的疲劳寿命预测一直是业界关注的重点。焊接接头疲劳寿命预测方法主要采用基于传统疲劳试验测定的S-N曲线法[3]。这种方法试验周期长、所需样本数量大及经济成本高,一直以来都是制约该方法应用的主要因素。因此,如何发展一种基于小样本疲劳试验数据快速测定S-N曲线的方法是业界关注的核心问题。
红外热像法具有实时、在线及非接触等特点,而被广泛应用于疲劳评估领域。在疲劳极限评估方面,Fargion等人[4]和Luong等人[5-6]提出了采用基于稳定温升步长的双线法疲劳极限预测模型,已被许多相关学者所证明[7-10]。樊俊铃等人[11]发展了基于能量耗散的材料疲劳极限评估方法,揭示了疲劳温升背后的不可逆能量耗散机理。在疲劳寿命预测领域,文献[12]提出了基于热像技术和能量耗散的点焊接头疲劳寿命预测模型;Guo等人[13]提出了基于红外热像法的S-N曲线模型;Liu等人[14]建立了基于能量耗散的点焊接头疲劳寿命预测模型。Li等人[15]研究了碳纤维复合材料试件的疲劳行为采用红外热像技术,该方法将疲劳温升三阶段的循环周次占全部疲劳寿命的比例,作为疲劳寿命评估的依据,为疲劳寿命评估提供了一种新思路。然而,尽管红外热像方法已经在疲劳评估领域取得了较好的进展。但是针对高周疲劳的研究较少,特别是针对焊接结构的评估鲜少涉及。Huang等人[16-18]认为对于高周疲劳而言,因疲劳过程中的滞弹性非常小以至于无法用设备监测到,而高周疲劳过程又是一个累积损伤不断增加的过程。
基于此,借助于红外热像技术,以Q460对接接头为研究对象,建立一种将焊接接头疲劳寿命、疲劳极限及统计学结合起来的S-N曲线快速预测模型。模型以能量耗散为索引,通过计算得到不同载荷下的单位时间能量耗散值,确定随载荷增加的能量耗散转折点,并以此进行疲劳极限预测。然后,考虑当载荷高于疲劳极限时,其全寿命周期内的能量耗散存在阀值,进行中值S-N曲线预测评估,并结合统计学中的极大似然法快速预测P-S-N曲线。模型的优势在于仅需有限试件即可完成焊接接头S-N曲线预测,且具有一定精度,为S-N曲线预测提供了一种新方法。
1 能量耗散理论基础
能量耗散伴随着高周疲劳过程,而这种能量耗散以试件标距部分温度逐渐升高的形式展现出来。结合热力学第一定律和热力学第二定律,试件标距内的局部热平衡方程可以定义为公式(1)[7,13,19]:
ρCT-kdiv(gradT)=d1+sthe+sic+re
(1)
式中:ρ是材料密度;C是材料比热容;T是实时温度;k是热导率;d1着材料的固有耗散,可表示为公式(2);sthe是热弹性源,可表示为公式(3);sic暗示着由内摩擦引起的热源,可表示为公式(4);re是外部体积热源。
d1=σ:D-ρψ,ε:ε-ρTψ,ε·α
(2)
sthe=ρTψ,T,ε:ε
(3)
sic=ρTψ,T,α·α
(4)
式中:σ是柯西应力张量;D代表着欧拉应变张量;ψ描述着亥姆霍兹自由能;ε是应变张量;α代表着内变量αj(j=1,2,…,n)。
根据文献[7,13,16]的假设,高周疲劳的固有耗散主要由两部分引起:①不可逆微塑性变化;②可恢复的材料微结构运动行为。对于第一部分而言,该部分能量耗散占据全部固有耗散的绝大多数,且由该部分不可逆的微结构变化引起的能量耗散,会导致试件出现不可逆的累积损伤增加;而对于第二部分而言(仅占全部固有耗散的很小部分),该部分可恢复的材料微观结构运动几乎不会增加试件内部的累积损伤。因此,就Q460焊接接头的高周疲劳过程,一些假设可以总结为:①C和k是材料常数,在高周疲劳过程中可以认为是恒定的;②由sthe热弹性源引起的温度变化可以忽略;③由内摩擦引起的热源sic和外部体积热源re可以忽略;④仅考虑沿焊缝纵向的温度场分布。
基于以上假设,试件标距内一维热平衡方程可以表示为公式(5):
(5)

(6)
因此,高周疲劳过程中稳定温升阶段单位周次内的能量耗散可通过公式(6)计算得到。
2 三参数S-N曲线预测模型
2.1 疲劳极限预测
对于一个高周疲劳过程,其温升进程总体上可以分为3个阶段,如图1所示。①温度迅速增加的第一阶段;②温升趋于稳定的第二阶段;③温度瞬间升高的第三阶段。
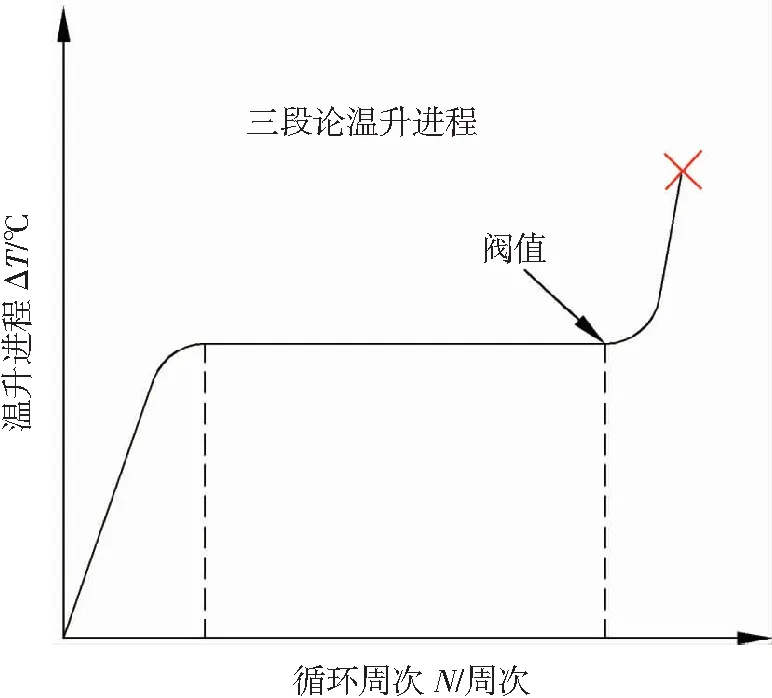
图1 标距部分疲劳温升过程示意图
Huang等人[8]在文献中报道,随着载荷(高于疲劳极限)的增加其稳定温升阶段疲劳温升值亦随之增加,如图2所示,并且随着载荷的增加试件的寿命会逐渐减小。

图2 不同载荷下疲劳温升进程示意图
鉴于上述内容,结合Fargione等人[4]和Luong等人[5-6]提出的双线法(如图3所示),Huang等人通过计算不同载荷等级下ΔTrstab完成了对材料疲劳极限的准确预测。但是,上述方法对于双线法转折点的确定仅基于视觉观察,没有确立一种基于数据的精确定位d1转折点的方法。为精确定位d1转折点,将不同载荷下的数据点按照载荷从小到大的顺序依次记为P1,P2,P3,…,Pi-1,Pi,Pi+1,…,Pn。然后,将相邻2条线段Pi-1,Pi和Pi,Pi+1之间的斜率差(见公式(7))绝对值变化最大位置处所对应的数据点,作为d1随载荷变化的转折点。此后,将全部数据点分成2组,分别进行线性拟合,将两线交点所对应的应力幅值作为疲劳极限的预测值。
ΔSi-1,i,i+1=|Si,i+1-Si-1,i+1|(i≥2)
(7)
式中:ΔSi-1,i,i+1是相邻2条线段斜率差的绝对值;Si,i+1和Si-1,i是相邻2条线段的斜率值。因此,基于提出的方法可以迅速确定d1随载荷变化的转折点,从而实现疲劳极限精确预测。

图3 基于能量耗散的疲劳极限预测模型
2.2 S-N曲线预测
图2中不同载荷下的疲劳温升进程呈现出2个基本特点:①随着载荷等级增加,试件的疲劳寿命趋于减小;②随着载荷等级增加,试件的稳定温升步长ΔTrstab趋于增加。Crupi等人[9]认为疲劳过程中存在能量阀值Ec,且该阀值可以表示为:
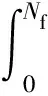
(8)
该模型仅是一个经验性的模型,并未将能量耗散理论纳入模型的建立当中。因此,基于Huang等人[16-18]和Guo等人[13]提出的基本假设,结合能量耗散模型(如1章节所述),从而实现Q460焊接接头的疲劳寿命预测与评估。
根据文献[7,8,10],当载荷高于材料的疲劳极限时,疲劳过程伴随着不可逆的累积损伤增加;而当载荷等级低于材料的疲劳极限时,其疲劳过程可认为几乎是不存在损伤,即可认为存在无限寿命(图4)。因此,全寿命周期能量耗散阀值模型可定义为:

(9)
式中:Ec为能量阀值;Δd1为引起累积损伤的耗散值;tf是疲劳时间。因为第二温升阶段占据约90%左右的疲劳寿命[13]。因此,公式(9)可以简化为:
Ec={d1(2)-d1(1)}×tf
(10)
式中:d1(1)和d1(2)分别为为相应应力幅下的能量耗散值,且因tf×f=Nf,于是公式(10)可以变形为公式(11):
(11)
上式中d1(2)可以由公式(12)得到:
(12)
式中:a2为拟合直线2的斜率;d1(2)为相应应力幅下的单位周次能量耗散值;d1f为载荷达到疲劳极限时对应的单位周次能量耗散值;Δσ为应力幅(高于疲劳极限);Δσf为疲劳极限。

图4 损伤模型示意图
结合公式(11)和(12),当载荷高于疲劳极限时,能量耗散阀值模型可以表示为:
(13)
当载荷接近疲劳极限时,其稳定温升阶段的能量耗散值非常小[20],因此d1f(2)-d1(1)可以认为是忽略不计的,上式简化为公式(14):
(14)
对于给定的应力幅下,试件因其初始状态的差异性从而导致疲劳寿命的分散性。因此,需对同一载荷下的能量耗散值进行平均化处理,并将平均值作为能量耗散阀值的估计值。即:
(15)

(16)
至此,一种基于能量耗散的三参数S-N曲线预测模型已经建立,该模型可实现中值S-N曲线快速预测。然而,上述模型仅给出存活率为50%的S-N曲线预测方法,对于存活率为95%的S-N曲线可结合统计学中的极大似然法计算得到[21]。
3 试验方法
3.1 试验材料
采用板厚为8 mm的Q460对接接头进行疲劳试验,采用MAG焊完成Q460对接接头的焊接,保护气体为80% Ar+20% CO2,坡口角度为55°,并对焊缝根部进行打磨以消除其根部缺陷的影响。Q460试验材料化学成分与热物理性能参数分别见表1和表2。

表1 Q460试验材料化学成分(质量分数,%)

表2 Q460试验材料热物理性能参数
3.2 疲劳试验
采用PLG-200高频疲劳试验机进行试验,试验过程的载荷模式为单轴正弦循环波动载荷,其试验频率为125 Hz,应力比为0.1。为保证试验稳定进行,需用紧固夹块将试件两端部夹紧。借助Fluke Ti450红外热像仪对试件标距部分进行实时温度监测,且为增强试件表面发射率,将黑色哑光漆均匀喷在试件(焊缝一侧)表面,试验相关装置及设备如图5所示。
结合第2章节所述模型,文中的疲劳试验可设计为:①采用应力幅值为8个等级下的试件,每级载荷下各测试一个试件,至到其发生断裂,将获得疲劳寿命数据用于模型验证;②基于第1章节中的能量耗散模型,计算①中试件第二阶段的单位周次内的能量耗散,完成疲劳极限的预测;③完成疲劳极限预测后,在高于疲劳极限以上的任一应力幅下再增加测试2个试件,得到该应力幅值下平均能量阀值,然后基于公式(14)实现中值S-N曲线预测,结合极大似然法完成P-S-N曲线预测。
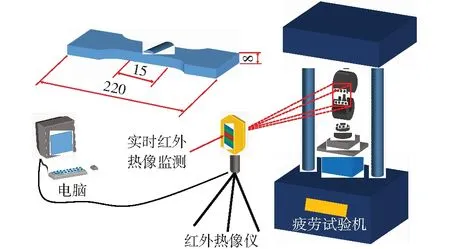
图5 试验设备及装置
4 试验结果
4.1 疲劳极限预测
如第2.1章节所述,一种基于能量耗散的精确测定材料疲劳极限模型已经建立,该模型优势在于只需得到每一级应力水平下的热像数据,即可完成材料疲劳极限的预测。因此,基于公式(7)可迅速确定d1转折点,从而完成不同载荷等级下能量耗散数据的分组,其疲劳极限预测结果如图6所示。图6中黄色菱形代表的是组1,蓝色菱形代表的是组2(经公式(6)计算得到当ΔSi-1,i,i+1当i=2时取得最大值)。拟合线1和拟合线2的R2分别为1和0.933 59,这表明其拟合程度较好,且拟合函数分别如公式(17)和公式(18)所示:
d1(1)=0.061 29Δσ-5.842 36
(17)
d1(2)=3.463 8Δσ-357.038 73
(18)
联立公式(17)和公式(18),得疲劳极限值为103.216 9 MPa。然后,为验证该方法的有效性,将其与传统的升降法结果进行对比(见表3),结果表明二者误差值仅为-1.35%,这暗示着热像法可以实现快速且具有一定精度的疲劳极限预测。

图6 基于能量耗散的疲劳极限预测

表3 基于热像法和升降法疲劳极限预测
4.2 S-N曲线评估
如第2.2章节所述,当载荷等级高于疲劳极限时,其累积损伤存在阀值,且该阀值可用于疲劳寿命预测模型建立,如公式(14)所示。然后,为实现快速预测不同存活率下的P-S-N曲线,结合第3.2章节中所述试验设计②,即在高于疲劳极限以上的某一应力幅(这里取135 MPa),取3个试件的能量耗散值进行平均处理,然后以此为阀值进行P-S-N曲线预测。经计算,3个载荷等级为135 MPa下试件疲劳全周期范围的能量耗散见表4,故得平均能量耗散阀值为4.26×105W/m3。

表4 应力幅为135 MPa下的3个试件能量耗散
结合上述结果以及获得的疲劳极限预测值,S-N曲线函数表达式可以写为公式(19),该公式可用于预测存活率为50%的S-N曲线,然后,结合极大似然法完成了存活率为95%的S-N曲线评估,如图7所示。
(Δσ-103.216 9)Nf=1.54×107
(19)
图7为预测的S-N曲线与试验结果的对比,其中红线代表的是存活率为50%的S-N曲线,黑线代表的是存活率为95%的S-N曲线,蓝色空心圈代表的是试验数据。从图7中可以看出,试验数据基本分布在存活率为50%的S-N曲线和存活率为95%的S-N曲线之间,这表明该利用提出第2.2章节提出的能量模型预测S-N曲线有着一定的精度,可以用于快速的S-N曲线预测以及疲劳寿命评估。
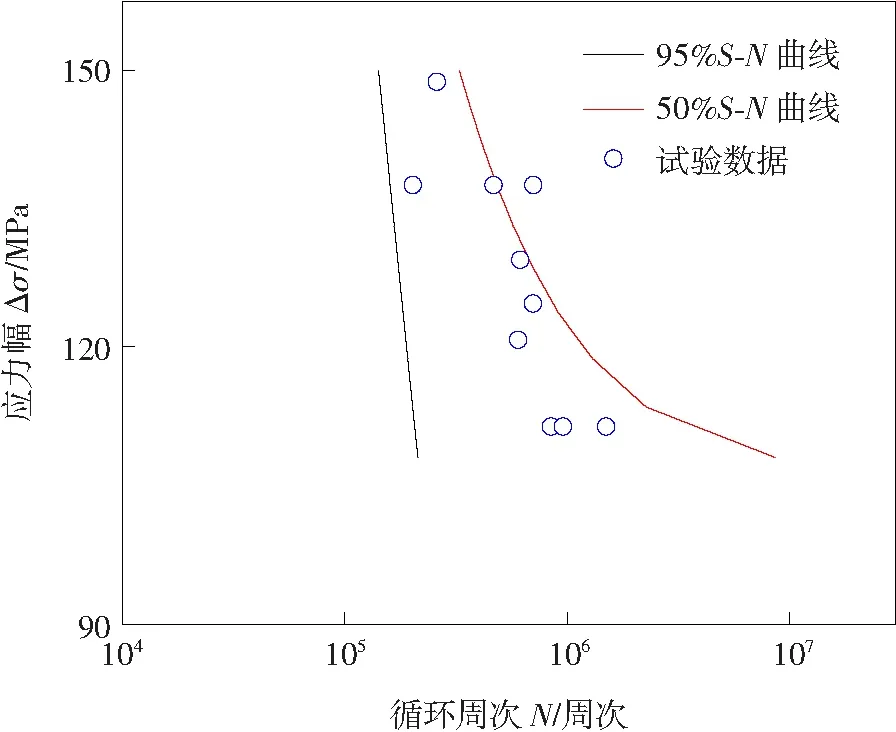
图7 预测S-N曲线与试验数据对比
5 结论
建立了一种基于能量耗散的S-N曲线快速预测模型。首先,基于稳定稳定温升阶段的能量耗散转折点实现了疲劳极限的精确预测。其次,借助于提出的基于能量耗散阀值理论的S-N曲线预测模型,完成了中值S-N曲线预测,并结合极大似然法得到了存活率为95%的S-N曲线。然后,将预测结果与试验结果对比,结果表明试验数据基本分布在50%曲线和存活率为95%的S-N曲线范围内,从而验证了模型的精确性,这为以有限试件快速完成S-N曲线的设计提供了一种新方法。

